为改进三维模型信息隐藏的鲁棒性,提出了一种基于OBJ(3D模型文件格式)三维模型纹理贴图的信息隐藏算法.选取三维模型贴图进行多元数小波变换;运用奇异值分解理论进行静态系数提取;利用三维Arnold置乱和纹理映射算法对隐秘信息和静态系数进行融合与正交投影.实验结果表明,算法能显著提高线框渲染、顶点绘制、面片挤出和剪切等攻击的鲁棒性.
An information hiding algorithm based on texture mapping of one kind of the document formats of 3D models (OBJ) is proposed in order to improve the robustness. First, 3D model texture maps are transformed into multivariate wavelet form. Second, the singular value decomposition theory is used to extract the multivariate wavelet static coefficients. Last, the secret information and the above static coefficients are merged by multiplication using the three-dimensional Arnold scrambling and texture mapping algorithm, and the merged coefficients are operated by orthographic projection to form the embedding regions. The experiment results indicated that the robustness against some attacks such as wireframe rendering, vertex rendering, patch extrusion, and shearing was improved, and the feasibility of this method was acceptable.
三维模型信息隐藏技术具有良好的不可见性和较高的容量性,如何提高三维模型信息隐藏的鲁棒性成为信息安全领域研究的热点[1-2]. Motwani等[3]结合传统二维图像隐藏算法,研究了三维数据冗余结构特性,提出较具代表性的三维模型隐藏技术.在提高不可见性和鲁棒性方面,Jiang等[4]将三维顶点坐标的小数映射为整数,利用比特流加密技术,对几个最低有效位嵌入数据进行操作,完成信息隐藏. Lee等[5]介绍了一种侧重于感知嵌入的三维数据水印算法.笔者提出的方案利用深度信息视觉特性,通过三维数据z轴上的运动与渲染操作完成信息的嵌入.张弢等[6]提出以模型骨架点及内切球解析次数作为隐秘信息的修改特征度量方式,抵抗旋转攻击的能力得到提高.上述三维模型隐藏算法虽然明显提高了不可见性和容量性,并具备抵抗一般攻击的鲁棒性,但基本都是以特征提取的思想将隐秘信息直接嵌入三维模型载体空间中,不能有效抵抗如剪切、面片挤出、线框渲染等特殊攻击,基于三维模型的信息隐藏算法也不能满足复杂的互联网应用环境.
在信息隐藏领域,传统多元数小波变换仅用于探索二维图像的渲染构造及处理,基本没有涉及不可见信息的嵌入和隐藏.算法旨在不局限于对二维载体数据进行信息嵌入,而是利用三维数冗余贴图特性克服上述算法鲁棒性不强的弱点.
1 信息隐藏算法步骤描述 1.1 OBJ模型贴图处理与隐秘图像处理OBJ三维模型支持贴图坐标与法线信息,文件内部组成数据如表 1所示.
|
|
表 1 OBJ模型文件内部数据 |
选取512×512的彩色Lena图像作为OBJ模型实验的纹理贴图,对其进行多元数小波变换,得到图像矩阵
| $ \mathit{\boldsymbol{Q}}=X_{\mathrm{R}} i+X_{\mathrm{G}} j+X_{\mathrm{B}} k $ | (1) |
其中:XR、XG、XB分别表示Lena图像像素中的R、G、B成分,i、j、k代表复数域系数.对Q进行第1次多元数小波分解,待输入的二维纹理贴图被分成16份子图区域块;第2次被分解成28份;第k次分解份数为
| $ {S_k} = 18k - 2{k^2} $ | (2) |
经分解变换的各区域纹理子图系数可组成系数矩阵
| $ \mathit{\boldsymbol{S}} = \left( {\begin{array}{*{20}{c}} {L{L_{{\xi _h}(x){\xi _h}(y)}}}&{L{H_{{\xi _h}(x){\psi _h}(y)}}}&{H{L_{{\psi _h}(x){\xi _h}(y)}}}&{H{H_{{\psi _h}\left( x \right){\psi _h}(y)}}}\\ {L{L_{{\xi _g}(x){\xi _g}(y)}}}&{L{H_{{\xi _g}(x)}}_{{\psi _h}(y)}}&{H{L_{{\psi _g}(x){\xi _h}(y)}}}&{H{H_{{\psi _g}\left( x \right), {\psi _h}(y)}}}\\ {L{L_{{\xi _h}(x){\xi _g}(y)}}}&{L{H_{{\xi _h}(x){\psi _g}(y)}}}&{H{L_{{\psi _h}(x){\xi _g}(y)}}}&{H{H_{{\psi _h}\left( x \right){\psi _g}(y)}}}\\ {L{L_{{\xi _g}(x){\xi _g}(y)}}}&{L{H_{{\xi _g}(x){\psi _g}(y)}}}&{H{L_{{\psi _g}(x){\xi _g}(y)}}}&{H{H_{{\psi _g}\left( x \right){\psi _g}(y)}}} \end{array}} \right) $ | (3) |
其中:ξ表示图像的局部移位信息,ψ代表图像的纹理特征,L和H分别代表各纹理子图的低、高频子带区域.矩阵S的列对应不同的多元数,如式(4)所示. 图 1(a)~(d)为第1次多元数小波变换后的分解子图.
| $ \left. \begin{array}{l} {s_1} = L{L_{{\xi _h}(x){\xi _h}(y)}} + iL{H_{{\xi _h}(x){\psi _h}(y)}} + jH{L_{{\psi _h}(x){\xi _h}(y)}} + kH{H_{{\psi _h}\left( x \right){\psi _h}(y)}}\\ {s_2} = L{L_{{\xi _g}(x){\xi _g}(y)}} + iL{H_{{\xi _g}(x)}}_{{\psi _h}(y)} + jH{L_{{\psi _g}(x){\xi _h}(y)}} + kH{H_{{\psi _g}\left( x \right), {\psi _h}(y)}}\\ {s_3} = L{L_{{\xi _h}(x){\xi _g}(y)}} + iL{H_{{\xi _h}(x){\psi _g}(y)}} + jH{L_{{\psi _h}(x){\xi _g}(y)}} + kH{H_{{\psi _h}\left( x \right){\psi _g}(y)}}\\ {s_4} = L{L_{{\xi _g}(x){\xi _g}(y)}} + iL{H_{{\xi _g}(x){\psi _g}(y)}} + jH{L_{{\psi _g}(x){\xi _g}(y)}} + kH{H_{{\psi _g}\left( x \right){\psi _g}(y)}} \end{array} \right\} $ | (4) |

|
图 1 多元数小波的一级分解与隐秘图像置乱加密情况 |
选取256×256的scene灰度图像O作为算法的隐秘信息,对其进行三维Arnold加密置乱. 图 1(f)中scene图像的置乱次数为10.三维置乱的作用是将二维隐秘信息转换成三维数据类型,此时的数据即可嵌入OBJ模型贴图的多元数小波系数空间中.
1.2 含密纹理贴图生成步骤步骤1 将式(3)中各子区域系数矩阵依照式(4)转化为对角矩阵Dij,按奇异值分解理论设置静态分解系数阈值,筛选各区域块相应最大静态系数值,得到新对角矩阵
步骤2 将压缩处理后的隐秘scene信息记为O′,随后经三维Arnold置乱生成隐秘图像O″,元素O″(i, j)以二进制比特的形式嵌入各子区域块
步骤3 将图像各子区域的多元数酉矩阵Uij、对角矩阵
| $ {\mathit{\boldsymbol{T}}_{ij}} = {\mathit{\boldsymbol{U}}_{ij}}{\mathit{\boldsymbol{\widetilde D}}_{_{ij}}}'\mathit{\boldsymbol{V}}_{ij}^{\rm{H}} $ | (5) |
其中:Uij∈Sm×n,m和n是四元数矩阵S的行与列数;VijH∈Sn×n.最终的含密贴图图像Q′为
| $ {\mathit{\boldsymbol{Q}}^\prime } = \left( {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\widetilde T}}}_{11}}}&{{{\mathit{\boldsymbol{\widetilde T}}}_{12}}}& \vdots &{{{\mathit{\boldsymbol{\widetilde T}}}_{1M}}}\\ {{{\mathit{\boldsymbol{\widetilde T}}}_{21}}}&{{{\mathit{\boldsymbol{\widetilde T}}}_{22}}}& \vdots &{{{\mathit{\boldsymbol{\widetilde T}}}_{2M}}}\\ \ldots & \ldots & \ddots & \vdots \\ {{{\mathit{\boldsymbol{\widetilde T}}}_{M1}}}&{{{\mathit{\boldsymbol{\widetilde T}}}_{M2}}}& \vdots &{{{\mathit{\boldsymbol{\widetilde T}}}_{MM}}} \end{array}} \right) $ | (6) |
选取Round table.stl模型作为最初的三维承载体,如图 2(a)和(b)所示.

|
图 2 stl与OBJ格式的Round table模型 |
应用正交投影的纹理映射规则可构造出带有表面颜色属性的OBJ模型.
步骤1 从材质库中选择标准纹理贴图素材,支持UV方式贴图的图像类型默认JPG格式.图像空间占比一般小于等于stl初始模型容量,对其进行定义和鲁棒区域划分.选定承载体三维模型后,进行三角面片投影准备.
步骤2 从步骤1中划分的鲁棒区域获取将要映射到stl模型面片表面的纹理信息,定义纹理坐标.
步骤3 建立贴图map与模型文件间的纹理坐标索引,建立纹理信息投影关联后进行正交投影.
步骤4 在仿真平台Autodesk 3Ds Max 2016上以standard标准将Round table模型赋上或更换为建筑材质.以default贴图标准选中含密贴图Q′,使用该平台默认的纹理映射算法将贴图图像投影在赋予材质的三维模型面片上,生成带有表面颜色等属性的完整含密模型.完整OBJ模型如图 2(c)和(d)所示.
2 仿真实验与对比分析选择图 1(e)为原始隐秘信息(256×256的scene灰度图像),以512×512的彩色Lena贴图图像Q为原始载体,生成含密贴图Lena图像Q′.选取Round table.stl模型作为含密贴图Q′的承载体,赋予其建筑材质,为待投影Round table模型作准备.实验环境为Autodesk 3Ds Max 2016,Matlab,Meshlab,VC++.
2.1 不可见性实验将隐秘信号叠加到OBJ三维模型载体贴图的多元数小波系数处,即分解的奇异值上,相当于在图像时频域的“阴影处”进行操作,作用效果体现在三维模型原始载体贴图的纹理细节与边缘处,使攻击者对物体局部细节的变化或微小改动不易察觉,满足人眼视觉特性(HVS, human visual system).选取Autodesk 3Ds Max 2016软件平台的默认映射方式将含密贴图进行正交投影,不可见性实验结果如图 3所示.

|
图 3 不可见性实验结果 |
主流的三维模型纹理映射与投影技术对物体细节处的表达和展现还远不成熟,将贴图图像的细节变动完全反映在三维模型表面还处于初级阶段,因此隐秘信息嵌入后几乎不会对三维模型的载体“表面贴图”造成变化,隐藏于鲁棒系数区域内的秘密信息不受影响,符合人在视觉上的不可感知性.
王新宇等[7-8]提出的分别为现今具有代表性的基于三维模型变换域与空间域算法,故将其作为本文算法不可见性的对比组.将隐秘消息嵌入载体前后模型变化的不可见性进行指标量化,利用Metro工具对Round table嵌入隐秘消息scene后的Hausdorff距离进行计算,置乱后隐秘消息scene转化的二进制比特量值为214.143 7 bit,此时其Hausdorff距离[9]为0.306×10-3.基于Hausdorff距离的不可见性对照实验情况见表 2.
|
|
表 2 嵌入信息比特量(2k) |
由统计结果可看出,当隐秘信息嵌入强度k为10~22时,本文算法的Hausdorff值明显比对照组算法小,不可见性更好;当k≥22时,本文算法的不可见性比文献[8]的算法稍弱,原因在于嵌入的隐秘消息容量大于222 bit时,原纹理贴图与含密纹理贴图在细节边缘处已经有变化,且该变化可以映射到模型表面上,并能被人眼所察觉.因此本文算法适用于空间占比小(嵌入信息的比特数不大于222 bit),多载体密度低的秘密文件传输.
2.2 鲁棒性实验将隐秘信息图像隐藏于三维模型的“表面贴图”中,利用三维模型可视化平台Autodesk 3Ds Max 2016将原含密贴图正交投影到模型表面,选取的三维承载体模型具有不同的拓扑结构,模型表面贴图也有不同的展示效果.奇异值矩阵运算使秘密消息隐藏区域与三维模型间的动态联系减小到最低程度.算法与承载体三维模型的顶点,拓扑关系等不相关,因而特殊攻击对含密贴图的影响极其有限.如图 4所示的仿真实验表明,在保持良好视觉效果的基础上,经本文算法构造的OBJ三维模型不仅100%抗旋转攻击,对诸如噪声攻击、顶点攻击、按面挤出、面片剪切、线框渲染等特殊攻击也具有较强的鲁棒性.

|
图 4 特殊攻击及信息提取 |
为客观衡量三维模型的鲁棒性,即OBJ模型贴图经纹理映射和正交投影后秘密消息的改变程度.采用式(7)中的比特数正确率(BCR,bit correct ratio)作为三维模型算法鲁棒性的数值评判标准,以变量κ表示.其中f为正确的秘密信息比特数,X为嵌入秘密信息的总比特数.
| $ \kappa = \frac{f}{X} $ | (7) |
在Auto desk 3Ds Max 2016和meshlab平台上,仿真含密OBJ贴图遭受特殊攻击,提取出的隐秘信息比特数如表 3所示.注:文章除0.1%随机加躁攻击在meshlab平台模拟实验外,其他鲁棒性攻击实验均在Auto desk 3Ds Max平台上进行,包括一般的旋转攻击等.本文算法着重对模型进行特殊攻击(面片挤出、剪切、顶点绘制、线框渲染等)的鲁棒性进行测试.结果表明,OBJ模型经受特殊攻击后,运用文章算法从三维模型含密贴图中提取的BCR比值均高于50%,远远大于鲁棒性最低阈值(BCR为10.08%),且均优于其他2种算法,因此算法的鲁棒性较强.
|
|
表 3 OBJ模型鲁棒性实验BCR数值 |
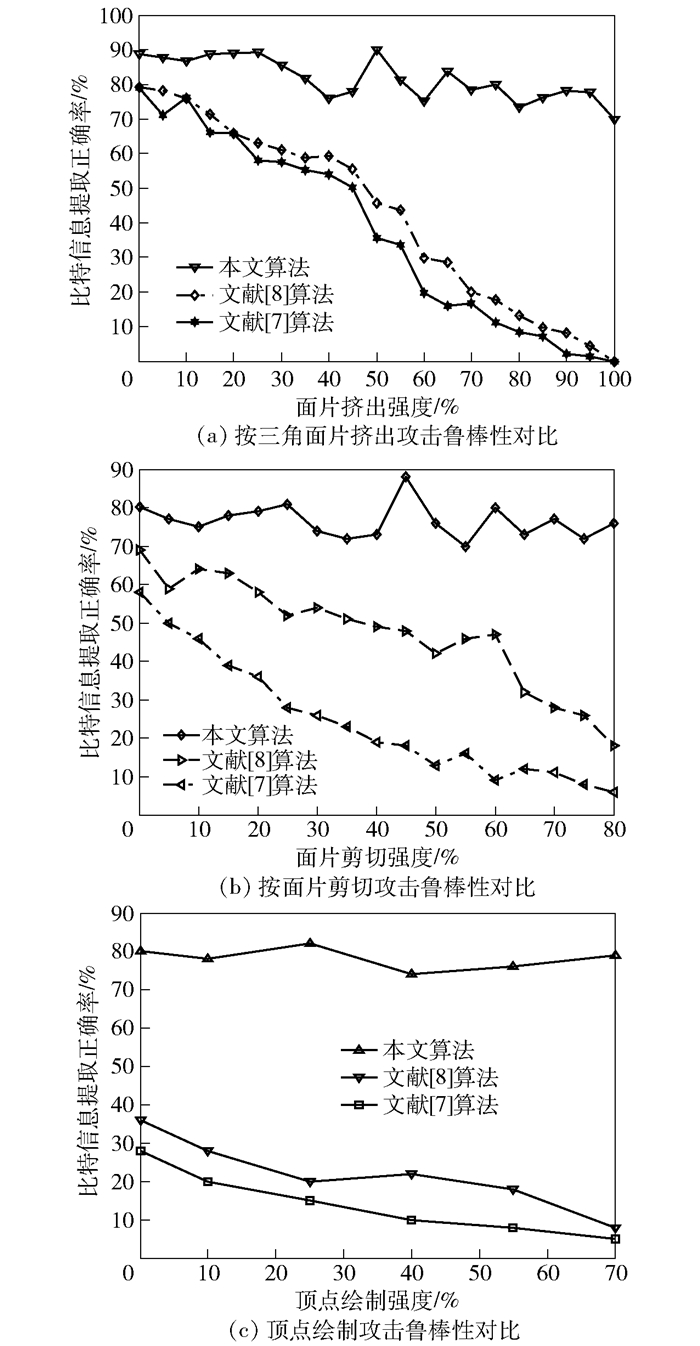
面片挤出攻击在三维模型鲁棒性研究中较为复杂,为重点分析OBJ模型经受该攻击的鲁棒性,在逐步增强此类型攻击强度的实验环境基础上也采用相同的对照组,实验结果如图 5(a)所示.笔者基于OBJ模型算法的比特正确率最高,鲁棒性较强.
|
图 5 鲁棒性对比实验 |
分析3种算法在不同强度剪切攻击下提取出的正确秘密信息,在仿真平台以按面剪切的形式进行不同程度面片剪切攻击,实验结果如图 5(b)所示.面片剪切区域占比为30%时,本文算法的BCR比值为75.14%,不仅在同领域算法中隐秘信息恢复程度最好,在对三维模型剪切攻击强度达到75%时,算法也具备较强的鲁棒性.
进行顶点绘制攻击,将Round table模型顶点分别进行10%、25%、40%、55%和70%强度的绘制重排实验,对比结果如图 5(c)所示.模型顶点绘制重排程度接近70%时,本文算法提取出的信息仍可以有效识别,BCR比值均大于50%,表明OBJ模型算法对顶点绘制攻击也具有较强的鲁棒性.
3 结束语基于多元数小波变换算法和奇异值变换理论,选取不受OBJ模型正交投影影响的原彩色纹理贴图作为信息隐藏的原始载体.利用奇异值矩阵运算的平移不变性等构造载体贴图隐秘空间,将含密贴图正交投影到模型表面后进行信息传递,满足三维模型可视化与信息隐藏技术的性能要求.仿真实验结果表明,算法适用于对鲁棒性要求较高的应用环境[10].然而,本文算法的隐秘信息嵌入容量敏感性[11]会因Auto desk 3Ds Max 2016与meshlab平台的功能性与时效性变化而变化.目前,贴图容量与初始stl三维模型面片表面承载阈值仍不能确定,且基于文件传输过程中的匹配加密[12]流程也需考虑,故在后续的研究中将着重建立该类算法的容量性评价体系.
| [1] |
雷敬祥.基于能量权重的信息隐写算法设计与研究[D].长安大学, 2016: 39-48. http://cdmd.cnki.com.cn/Article/CDMD-10710-1016749405.htm
|
| [2] |
綦科, 张大方, 谢冬青. 基于帧化采样和小波HMM的三维模型信息隐藏[J]. 计算机辅助设计与图形学学报, 2010, 22(8): 1406-1411. Qi Ke, Zhang Dafang, Xie Dongqing. Steganography for 3D model based on frame transform and HMM model in wavelet domain[J]. Journal of Computer-Aided Design and Computer Graphics, 2010, 22(8): 1406-1411. |
| [3] |
Motwani R, Motwani M, Jr F H. An intelligent learning approach for information hiding in 3D multimedia[C]//International Conference on Future Networks. Sanya: IEEE Computer Society, 2010: 447-451. http://www.researchgate.net/publication/228913473_An_Intelligent_Learning_Approach_for_Information_Hiding_in_3D_Multimedia
|
| [4] |
Jiang R, Hang Z, Zhang W, et al. Reversible data hiding in encrypted 3D mesh models[J]. IEEE Transactions on Multimedia, 2017(99): 181-186. |
| [5] |
Lee M J, Lee J W, Lee H K. Perceptual watermarking for 3D stereoscopic video using depth information[C]//International Conference on Intelligent Information Hiding & Multimedia Signal Processing. Dalian: IEEE, 2011: 81-84. http://www.researchgate.net/publication/221566157_Perceptual_Watermarking_for_3D_Stereoscopic_Video_Using_Depth_Information
|
| [6] |
张弢, 慕德俊, 任帅, 等. 利用内切球解析的三维模型信息隐藏算法[J]. 西安电子科技大学学报(自然科学版), 2014, 41(2): 185-190. Zhang Tao, Mu Dejun, Ren Shuai, et al. Information hiding scheme for 3D models based on skeleton and inscribed sphere analysis[J]. Journal of Xidian University (Natural Science), 2014, 41(2): 185-190. DOI:10.3969/j.issn.1001-2400.2014.02.030 |
| [7] |
王新宇, 詹永照. 构造顶点分布特征的三维模型数字水印算法[J]. 计算机辅助设计与图形学学报, 2014, 26(2): 272-279. Wang Xinyu, Zhan Yongzhao. A watermarking scheme for three-dimensional models by constructing vertex distribution characteristics[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(2): 272-279. |
| [8] |
杨飚, 吕梦琪, 王宜敏, 等. 基于复杂区域多层嵌入的三维模型隐写[J]. 电子测量技术, 2016, 39(12): 164-167. Yang Biao, Lü Mengqi, Wang Yiming, et al. Structure complexity based multi-layer steganography for 3D model[J]. Electronic Measurement Technology, 2016, 39(12): 164-167. DOI:10.3969/j.issn.1002-7300.2016.12.035 |
| [9] |
Carlson N A, Porter J R. On the cardinality of Hausdorff spaces and H-closed spaces[J]. Topology & Its Applications, 2013, 160(1): 137-142. |
| [10] |
Salimi A, Lowther D A. On the role of robustness in multi-objective robust optimization:application to an IPM motor design problem[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1-4. |
| [11] |
Sedighizad M, Bafghi H G, Seyfe B. Sensitivity of the secrecy capacity of a wiretap channel to the channel gains with imperfect channel information[C]//2017 Iran Workshop on Communication and Information Theory (IWCIT). Tehran: IEEE, 2017: 1-5.
|
| [12] |
Sruthi S, Vijay A, Jose S, et al. Encryption & decryption of text file and audio using LabVIEW[C]//International Conference on Networks & Advances in Computational Technologies. Thiruvanthapuram: IEEE, 2017: 462-466. http://www.researchgate.net/publication/320662245_Encryption_decryption_of_text_file_and_audio_using_LabVIEW
|



