2. 北京邮电大学 现代邮政学院, 北京 100876
经典物流配送模型的目标、约束条件不够全面,在实际应用中存在一定缺陷,对此,构建了时间窗和油耗取送一体化的物流配送路径优化模型(PDVRPTF).设计了一种基于k-medoids动态聚类混合拓扑结构粒子群算法,解决了经典粒子群算法在求解此类模型时容易陷入局部最优解的问题.仿真结果表明,改进型粒子群算法能很好地跳出局部最优解,并快速收敛于全局最优解,且该算法可有效求解物流配送路径优化的问题.
2. School of Modern Post, Beijing University of Posts and Telecommunications, Beijing 100876, China
Aiming at the problem that the classic logistics distribution model considers the target, the constraints are not comprehensive enough and there are certain defects in the practical application, a integrated pickup and distribution vehicle routing problem on the basis of the classical model considering time window and fuel consumption (PDVRPTF) is constructed. Hybrid topological structure of particle swarm optimization based on k-medoids dynamic clustering is designed, which solves the problem that classical particle swarm optimization is easy to fall into local optimal solution when solving such models. The simulation results show that the improved particle swarm optimization can jump out of the local optimal solution quickly and converge to the global optimal solution quickly, which solve the logistics distribution path optimization problem effectively.
经典物流配送模型的目标和约束条件不够全面,在实际应用中存在一定缺陷,对此,提出了时间窗和油耗取送一体化物流配送路径优化模型(PDVRPTF,integrated pickup and distribution vehicle routing problems considering time window and fuel consumption),并将其用于解决实际问题,这样很大程度上减少了车辆的空载率和油耗,不但能够为企业降低成本,也能减少燃油资源的消耗和污染气体的排放,有利于绿色物流的发展.
对于求解路径优化问题,粒子群优化算法实现简单,计算效率高,在搜索前期收敛速度较快,但后期容易陷入局部最优解.针对这一问题,国内外很多学者提出了很多改进方式,如加入收敛因子[1]、采用不同的拓扑结构[2]和加入惯性因子[3]等.笔者将k-medoids聚类分析算法与粒子群结合,聚类之后采用all-ring型拓扑结构进行信息交流.利用Rastrigin函数验证算法的可行性,并利用Solomon标准数据集测试模型的实用性.
1 PDVRPTF问题模型 1.1 问题描述对PDVRPTF问题的基本描述如下:假设有n个客户,每个客户的位置和需求已知,配送中心有K辆额定车载量为Q的车.车辆配送优化模型要求从配送中心选出k(k=1, 2, …,K)辆车服务n个有送货或取货需求的客户,要求使用尽量少的车辆为所有的客户服务,每辆车在为客户取送货途中车载量不能超过额定车载量Q.在满足用户要求下,制定合理的车辆配送路线,使路程、时间和油耗等综合成本达到最少.
1.2 模型重要约束分析在建立PDVRPTF问题模型之前,需要对以下几个约束条件分别进行讨论.
1.2.1 时间窗约束每个客户点都有规定的时间窗[Ei, Li],其中接受服务的最早时间为Ei,最晚时间为Li,且每个点的服务时间为Si.
如果车辆k到达i点的时间Aik小于Ei,则车辆k要等待的时间为Wik,Wik=max{0, (Ei-Aik)};当车辆k到达i点的时间Aik在[Ei, Li]区间, 则直接服务i客户,不用付出等待时间;车辆k到达i点的时间Aik大于Li, 则其延迟的时间为Tik,Tik=max{0, (Aik-Li)}.
车辆k离开i的时间Dik为
| $ D_i^k = \left\{ {\begin{array}{*{20}{l}} {A_i^k + W_i^k + {S_i},}&{A_i^k < {E_i}}\\ {A_i^k + {S_i},}&{A_i^k \ge {E_i}} \end{array}} \right. $ | (1) |
车辆k的额定车载量约束为Q,取送一体化的服务方式需要保证车辆在路径的每一个点的车载量都不大于Q.设用户i的送货量为ci,取货量为pi,若车辆k的行驶路径为U0k,该行驶路径中车辆k需要服务的客户总数为Uk,则车辆k需要满足以下约束:
| $ \sum\limits_{i = 1}^{{U^k}} {{c_i}} \le Q $ | (2) |
| $ \sum\limits_{i = 1}^{{U^k}} {{p_i}} \le Q $ | (3) |
| $ \sum\limits_{i = 1}^m {{p_i}} + \sum\limits_{i = m + 1}^{{U^k}} {{c_i}} \le Q,m = 1,2, \cdots ,{U^k} $ | (4) |
式(2)表示保证路径U0k所有客户的送货量之和不超过额定车载量Q;式(3)表示保证路径U0k的全部取货量之和不超过额定车载量Q;式(4)表示保证车辆k在用户m处卸货并完成装货后的车载量不超过额定车载量Q.
1.2.3 油耗约束车辆的油耗不仅与车辆行驶的路程有关,而且与车辆发动机负荷率、行驶阻力、车辆的行驶状况、保养情况等因素相关.汽车等速行驶百公里油耗[4]为
| $ {R_s} = \frac{{P{b_0}}}{{1.02v\rho g}} = \frac{{{C_0}{F_0}{b_0}}}{\tau } $ | (5) |
其中:P为汽车行驶过程中遇到的阻力功率,b0为燃油消耗率,v为车辆的行驶速度,ρ为燃油的密度,g为重力加速度, C0为常数,F0为车行驶途中的阻力,τ为传动效率.由式(5)可知,汽车百公里燃油消耗量正比于等速行驶时的行驶阻力和燃油消耗率.
本模型假设车辆的行驶状况、保养情况和路面的摩擦等因素一定,汽车的载重量越大,所遇到的摩擦阻力越大,燃油消耗量也就越大.笔者仅考虑车辆的行驶里程和车辆的车载量对油耗的影响,且假设油耗和车辆的行驶里程、载量存在一定的线性关系,因此可利用“载重估计法”对油耗进行计算.若r*为车辆满载时行驶单位距离的油耗,r0为车辆空载时行驶单位距离的油耗,则车辆k在对路线U0k中第m个客户进行服务后车辆载重量qm的计算公式为
| $ {q_m} = \sum\limits_{i = 1}^m {{p_i}} + \sum\limits_{i = m + 1}^{{U^k}} {{c_i}} $ | (6) |
车辆在车载量为qm时行驶单位距离的油耗r(qm)计算公式为
| $ r\left( {{q_m}} \right) = {r_0} + \left( {{r^*} - {r_0}} \right)\frac{{{q_m}}}{Q} $ | (7) |
在车载量为qm时,车辆从点i行驶到点j的路程为dij,消耗的油耗Rij计算公式为
| $ {R_{ij}} = r\left( {{q_m}} \right){d_{ij}} = \left[ {{r_0} + \left( {{r^*} - {r_0}} \right)\frac{{{q_m}}}{Q}} \right]{d_{ij}} $ | (8) |
将式(8)引入PDVRPTF模型,将引导车辆先服务距离近、配送量大、货量小的客户,以降低车辆的油耗,使得车辆k的行走路径更加合理.
1.3 PDVRPTF模型构建目标函数:
| $ \begin{array}{*{20}{c}} {\min Z = {c_1}\sum\limits_{k = 1}^K {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{N + 1} {\left( {x_{ij}^k{d_{ij}}} \right)} } } + }\\ {{c_2}\sum\limits_{k = 1}^K {\sum\limits_{i = 1}^N {\left( {Y_i^kW_i^k} \right)} } + {c_3}\sum\limits_{k = 1}^K {\sum\limits_{i = 1}^N {\left( {Y_i^kT_i^k} \right)} } + }\\ {{c_4}\sum\limits_{k = 1}^K {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{N + 1} {R_{ij}^k} } } } \end{array} $ | (9) |
除1.2节中所给出的约束条件(1)~(8)之外,该模型的其他约束条件如下.
| $ x_{ij}^k = \left\{ \begin{array}{l} 1,\;\;\;车辆\;k\;从路线\;U_0^k\;的\;i\;行驶到\;j\\ 0,\;\;\;其他\;i \ne j,k \in K \end{array} \right. $ | (10) |
| $ Y_i^k = \left\{ \begin{array}{l} 1,\;\;\;车辆\;k\;服务路线\;U_0^k\;的客户\;i\\ 0,\;\;\;其他\;k \in K \end{array} \right. $ | (11) |
| $ D_i^k > A_i^k > D_{i - 1}^k $ | (12) |
| $ P_{ij}^k = \frac{{d_{ij}^k}}{v} $ | (13) |
| $ A_i^k = D_{i - 1}^k + P_{\left( {i - 1} \right)i}^k $ | (14) |
| $ \sum\limits_{i = 1}^N {x_{ih}^k} - \sum\limits_{j = 1}^{N + 1} {x_{hj}^k} = 0,h \in N,k \in K $ | (15) |
| $ \sum\limits_{k = 1}^K {Y_i^k} = 1,i = 1,2, \cdots ,N $ | (16) |
| $ \sum\limits_i^N {x_{ij}^k} = Y_j^k,j = 0,1,2, \cdots ,N,\forall k $ | (17) |
| $ \sum\limits_{j = 1}^N {x_{ij}^k} = Y_i^k,i = 0,1,2, \cdots ,N,\forall k $ | (18) |
式(9)是模型的目标函数,即在考虑车辆行走总路程、等待时间、延迟时间、油耗等因素的情况下,使总成本达到最小,其中Tik表示车辆k在用户i处的延迟时间,dij表示从i行驶到j的路程,c1、c2、c3、c4分别表示车辆行驶单位距离、等待单位时间、延迟单位时间、单位油耗所花费的成本;式(10)、式(11)为车辆k经过客户点的记录函数;式(12)表示车达到客户i的时间小于离开户i的时间,且大于离开客户(i-1)的时间;式(13)中Pijk表示车辆从客户i到客户j的行驶的时间,其中v为行驶速度,d(i, j)k表示车辆k从i行驶到j的行驶路程;式(14)表示车k到达某一点的时间为上一点的离开时间与路上消耗时间之和;式(15)表示到达某一点的车k只能从该点出发;式(16)~(18)为车辆k到达某一点的唯一性约束,即每一个点仅由一辆车服务.
2 基于混合拓扑结构k-medoids动态聚类的粒子群算法在粒子群优化算法(PSO,particle swarm optimization)中,粒子的状态包括2个向量:速度和位置.设搜索空间为d维,第i个粒子的速度向量Vi=[vi1, vi2,…,vid], 位置向量Xi=[xi1, xi2,…,xid], 第i个粒子迄今搜索到的最优解pb=[pi1, pi2, …, pid], 所有粒子目前搜索的全局最优解为gb=[gi1, gi2, …, gid], 粒子的速度更新公式如式(19)所示,位置更新公式如式(20)所示.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_{i + 1}} = \omega {\mathit{\boldsymbol{V}}_i} + {b_1}rand\left( {{\mathit{\boldsymbol{p}}_{\rm{b}}} - {\mathit{\boldsymbol{X}}_i}} \right) + }\\ {{b_2}rand\left( {{\mathit{\boldsymbol{g}}_{\rm{b}}} - {\mathit{\boldsymbol{X}}_i}} \right)} \end{array} $ | (19) |
| $ {\mathit{\boldsymbol{X}}_{i + 1}} = {\mathit{\boldsymbol{X}}_i} + {\mathit{\boldsymbol{V}}_{i + 1}} $ | (20) |
其中:ω为惯性权重,表示粒子上一位置的速度对当前位置搜索速度的影响程度;b1、b2为加速系数,分别表示粒子受个体认知和社会模式影响程度;rand是0~1之间的随机数.
针对取送结合的考虑油耗和时间窗的车辆配送路径优化模型,笔者设计改进型粒子群算法,用于求解物流配送车辆路径优化问题.
2.1 动态种群分割策略粒子群算法中粒子在不断搜索迭代的过程中收敛于全局极值gbi和个体极值pbit之间,考虑到算法的粒子具有聚集性[5],因此将聚类算法与粒子群算法有效结合.基于粒子的位置信息,以粒子间的距离作为度量,以各个粒子到各自聚类中心的距离之和最小化为目标,对种群进行k-medoids聚类.本文中k-medoids聚类利用k-medoids++选取k个粒子作为聚类中心(a1, a2,…,ak), 这样选取的聚类中心粒子距离较远,差异性较大,解决k-medoids算法中初始粒子选择不当导致簇效果不佳或收敛速度慢的问题;由于初选的聚类中心距离远,可保持簇间的差异性,有利于跳出局部最优解. d2(x, y)表示2个不同粒子之间欧几里得距离的平方,此处x、y分别表示2个不同的粒子,计算公式如式(21)所示,聚类迭代使得簇内误差平方和(E)最小,计算公式如式(22)所示.
| $ {d^2}\left( {x,y} \right) = \sum\limits_{j = 1}^d {{{\left( {{x_j} - {y_j}} \right)}^2}} = \left\| {x - y} \right\|_2^2 $ | (21) |
| $ E = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^k {{w^{\left( {i,j} \right)}}} } = \left\| {{x^{(i)}} - {u^{(j)}}} \right\|_2^2 $ | (22) |
其中u(j)为簇j的聚类中心点,如果x(i)属于簇j, 则w(i, j)=1,否则w(i, j)=0.
基于动态种群分割策略的聚类步骤如下:
步骤1 初始化空集合M,储存选定的k个聚类粒子点,从初始粒子中选第一个中心点u(j),并加入集合M,对集合M外的任一粒子x(i),通过计算找到与其平方距离最小的粒子d2(x(i), M), 并使用加权概率分布
步骤2 根据d2(x, y)将每个粒子划分到距离最近的中心点u(j)(j∈{1, 2, …, k})所代表的簇中,用各簇的中心点替代原来的中心点;
步骤3 重复步骤2的迭代过程,直到各簇的中心点位置不变或达到预定迭代次数,则聚类算法终止并输出聚类簇.
2.2 基于动态邻域的粒子速度在粒子聚类成簇之后,计算粒子的适应度,在簇j中选取适应度值最优的粒子作为该簇的最优解,并标记为Hj,比较簇j相邻簇最优解的大小,并将邻簇最优解记为Lb.对簇j中所有的粒子i而言,邻簇最优解的粒子记为Lb, i,Lb, i=(Lb, i1, Lb, i2, …, Lb, id).考虑到邻域最优解、自身最优解和全局最优解对粒子信息的影响,改进后的粒子群算法速度更新公式如式(23)所示.位置更新公式仍采用经典的位置更新公式,见式(20).
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_{i + 1}} = \omega {\mathit{\boldsymbol{V}}_i} + {b_1}rand\left( {{\mathit{\boldsymbol{p}}_{\rm{b}}} - {\mathit{\boldsymbol{X}}_i}} \right) + {b_2}rand\left( {{\mathit{\boldsymbol{g}}_{\rm{b}}} - {\mathit{\boldsymbol{X}}_i}} \right) + }\\ {{b_3}rand\left( {{\mathit{\boldsymbol{L}}_{{\rm{b}},i}} - {\mathit{\boldsymbol{X}}_i}} \right)} \end{array} $ | (23) |
这种改进后的速度更新公式引进了邻簇最优解对粒子的影响,解决了粒子群算法中粒子朝着初始粒子的全局最优gb聚集而陷入局部最优解的问题.
2.3 拓扑结构拓扑结构对算法的性能和精确度有很大影响,目前研究的种群拓扑结构主要有全局、局部、4类和金字塔.
考虑对粒子聚类后采用all-ring混合型拓扑结构,聚类簇内采用all型拓扑结构,粒子间相互连接,聚类簇之间采用ring型拓扑结构连接. all-ring拓扑结构增加了邻域最优解的影响,解决了所有粒子仅向当前种群最优粒子靠近而容易陷入局部最优解的问题,且在提升求解精度的同时,算法能保持较快的收敛速度.
2.4 自适应调整策略定义1 将第i簇记为Ai, Ci表示第i簇粒子的个数,fij表示第i簇中第j个粒子的适应度的值;对于目标函数求极大值的问题,适应度函数取目标函数,而求极小值的问题,适应度函数则取目标函数的相反数;第i簇适应度平均值Fi的计算公式为:Fi=
定义2 设ωmax为算法的最大惯性权重,ωmin为算法的最小惯性权重,算法的惯性权重ω根据ωmax,ωmin和迭代次数进行调整.
粒子群算法在不同的搜索时期,粒子处于不同的解位置.粒子处于较好位置,应该赋予较小的惯性权重,增强该粒子周围搜索力度;粒子处于较劣位置,应该赋予较大的惯性权重.聚类后的簇之间的粒子存在较大的差异性,根据每个簇的适应度平均值和种群适应度平均值的比较,赋予粒子不同的惯性权重.
若Fi<B, 说明i簇粒子处于较差的位置,应该赋予较大的惯性权重, 以提高全局搜索能力, 防止陷入局部最优解. Tmax表示最大迭代次数,l表示当前迭代次数,ω的变化方式为
| $ \omega _i^{t + 1} = \omega _i^t + \left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {\frac{{{T_{\max }} - l}}{{{T_{\max }}}}} \right) $ | (24) |
若Fi≥B, 说明该簇粒子处于较好的位置,应该赋予较小的惯性权重,以提高局部搜索能力, ω变化方式为
| $ \omega _i^{t + 1} = \omega _i^t - \left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {\frac{{{T_{\max }} - l}}{{{T_{\max }}}}} \right) $ | (25) |
改进型粒子群算法具体实现步骤如下.
1) 初始化粒子位置x、速度v0,初始种群包括粒子个数n、最大迭代次数Tmax、最大惯性权重ωmax和最小惯性权重ωmin,加速系数b1、b2、b3和初始惯性权重ω;
2) 采用2.1中的聚类方法对粒子进行聚类,确定k个簇,第i个簇记为Ai;
3) 计算第i个粒子的适应度值fi,记录当前各个体搜索到的最优pbi和全局最优gb,将第i簇中的最优粒子记为本簇的最优值Zi, i=1, 2, …, k;
4) 计算每个簇的适应度平均值Fi和全局适应度平均值B, 判断Fi和B之间的关系,根据式(24)或式(25)调整惯性权重ω;
5) 对簇i, 比较Zi-1, Zi+1, 将较大的值作为当前簇的Lb, 采用式(20)、式(23)调整粒子的位置和速度;
6) 计算粒子的适应度值,并记录当前粒子的最优值gb, 判断是否达到最大迭代次数Tmax或搜索到满意解,满足条件则停止迭代;否则重复步骤2)~6)进入下一轮迭代.
3 仿真测试分析与验证 3.1 Rastrigin函数实验选定PSO和笔者设计的基于混合拓扑结构k-medoids动态聚类的PSO(KPSO),运用Matlab建立仿真模型,求解Rastrigin函数.
Matlab仿真求解函数迭代图如图 1所示.
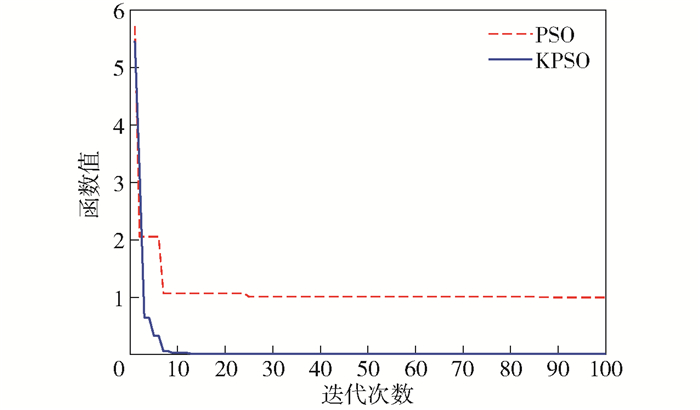
|
图 1 Rastrigin函数求解迭代图 |
由图 1可以看到经典PSO在Iteration为7时收敛,但粒子在适应度值为1附近陷入局部最优解,KPSO在Iteration为9时收敛到最优解附近,具有更好的跳出局部最优解的能力.
图 2和图 3分别为改进前后的粒子群算法迭代到Iteration为10时粒子分布图.
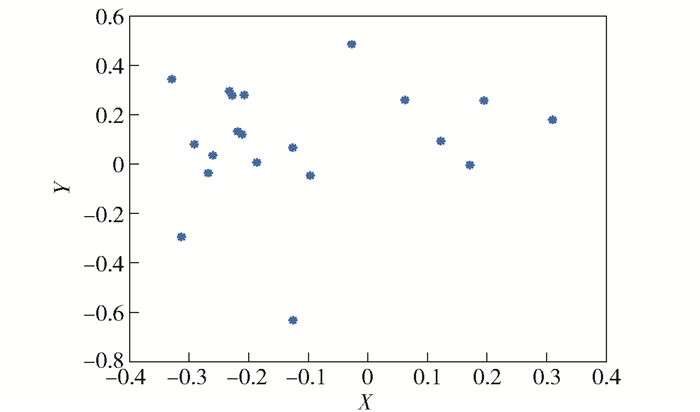
|
图 2 PSO算法粒子聚集图 |
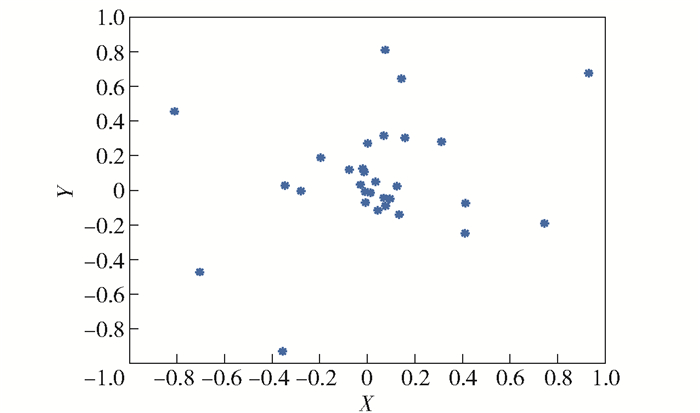
|
图 3 KPSO算法粒子聚集图 |
可以看出,KPSO粒子朝着最优值方向聚集,粒子间具有较大的差异性,而PSO中几个种群主要聚集在坐标轴的第2象限.陷入局部最优解中,难以进行进一步搜索,这也显示了PSO容易陷入局部最优的缺陷.
3.2 物流配送路径优化模型求解仿真采用Solomon标准数据集中R101的数据集作为实验数据,笔者按比例随机选取60%用户有同时取货送货的需求,对于取货需求将采取随机生成的方法添加.
其仿真参数为:最大迭代次数Tmax=100,惯性权重采用经典的线性调整,即最大惯性权重ωmax=0.9,最小惯性权重ωmin=0.4,初始惯性权重ω=0.9,粒子数n=50, 加速系数采用经典粒子群中的加速系数,b1=2,b2=2,邻域加速系数b3=1, 聚类簇k=3,假设c1=0.3,c2=0.1, c3=0.3,单位油耗成本c4=0.3,车辆满载时行驶单位距离的油耗r*=1,车辆空载时行驶单位距离的油耗r0=0.5,车辆的运行速度v=5 m/s2.利用Matlab仿真求解,迭代收敛图如图 4所示.
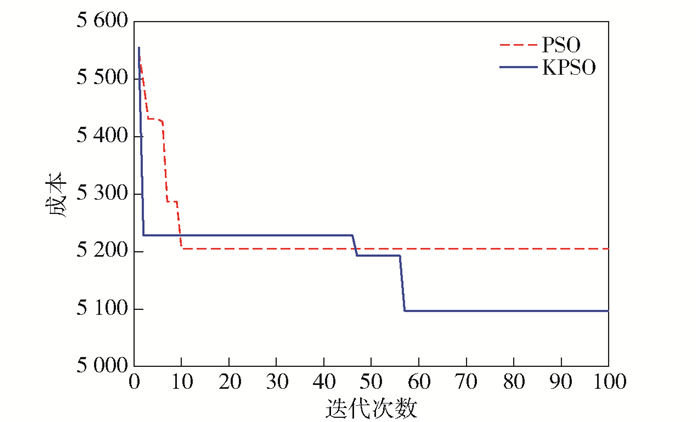
|
图 4 配送模型迭代收敛图 |
由图 4可以看出PSO在Iteration为10时陷入局部最优解,KPSO在Iteration为46时跳出了局部最优解,且能搜索到更优解,对解决物流调度问题具有更大的优势.
由上面的仿真算例可以看出,改进后的粒子群算法具有很好的跳出局部最优解的能力,并能够较好地解决PDVRPTF的问题.
4 结束语针对传统的车辆路径优化模型的缺点和经典粒子群算法容易陷入局部最优的不足,详细分析了油耗、时间窗、取送一体化等约束条件,并在此基础上构建相应的PDVRPTF数学模型.同时基于k-medoids对粒子群算法中的粒子动态聚类,采用all-ring型拓扑结构设计改进粒子群算法, 并分别用经典粒子群算法和改进后粒子群算法求解Rastrigin函数和Solomon改进数据集的车辆调度问题.测试结果表明,改进后的粒子群算法能够很好地跳出局部最优解,可以较好地优化多目标的车辆调度问题.
| [1] |
Shi Y H, Eberhart R. A modified particle swarm optimizer[C]//Proceedings of the IEEE Conference on Evolutionary. Computation, Anchorage: IEEE, 1998: 69-73. http://www.researchgate.net/publication/3755900_Modified_particle_swarm_optimizer
|
| [2] |
Xie X F, Zhang W J, Yang Z L. Adaptive particle swarm optimization on individual level[C]//International Conference on Signal Processing. Beijing: IEEE, 2002: 1215-1218. http://d.wanfangdata.com.cn/Conference/WFHYXW32724
|
| [3] |
王俊伟, 汪定伟. 粒子群算法中惯性权重的实验与分析[J]. 系统工程学报, 2005, 20(2): 194-198. Wang Junwei, Wang Dingwei. Experiments and analysis on inertia weight in particle swarm optimization[J]. Journal of Systems Engineering, 2005, 20(2): 194-198. DOI:10.3969/j.issn.1000-5781.2005.02.015 |
| [4] |
余志生. 汽车理论[M]. 第3版. 北京: 机械工业出版社, 2000: 42-45.
|
| [5] |
杨韬, 邵良杉. 采用改进的k均值聚类分析策略的粒子群算法[J]. 计算机工程与应用, 2009, 45(12): 52-54. Yang Tao, Shao Liangshan. Hybrid particle swarm optimization employing improved k-means clustering analysis strategy[J]. Computer Engineering and Applications, 2009, 45(12): 52-54. DOI:10.3778/j.issn.1002-8331.2009.12.017 |



