2. 桂林电子科技大学 广西无线宽带通信与信号处理重点实验室, 桂林 541004;
3. 燕山大学 信息科学与工程学院, 秦皇岛 066004
提出一种简单结构的双频带带通滤波器,由不等长十字形谐振器和平行耦合线馈电结构组成.由于滤波器分布电路具有对称性,首先利用奇偶模分析法对带通滤波器奇偶模输入阻抗、传输零点和传输极点进行分析.所设计的滤波器具有3个传输零点和4个传输极点.传输零点的位置不随阻抗参数的变化而变化.在4个传输极点中,第1个偶模传输极点和第1个奇模传输极点构成了第1个通带,剩下2个传输极点构成了第2个通带.与等长十字形谐振器滤波器相比,该结构多了一个极点.滤波器的通带带宽可以通过调节传输极点位置进行调整.给出了滤波器实物的结构参数,并且利用仿真软件进行仿真优化,得到了滤波器插入损耗和回波损耗的仿真结果.制作和测试了滤波器,给出了测试结果.仿真结果和测试结果基本上一致,验证了设计理论的正确性.
2. Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing, Guilin University of Electronic Technology, Guilin 541004, China;
3. School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China
A simple dual-band band-pass filter is proposed. It is composed of an unequal-length cross-shaped resonator and parallel coupled lines feed structures. Due to the symmetry of the filter distribution circuit, the transmission zero and transmission pole are analyzed using the even-odd mode analysis method. The designed filter has 3 transmission zeros and 4 transmission poles. The positions of the transmission zeros do not change with the changing of the impedance parameters. Among 4 transmission poles, the first even-mode transmission pole and the first odd-mode transmission pole constitute the first passband, and the remaining two transmission poles constitute the second passband. Compared with the equal-length cross-shaped filter, this structure has one extra transmission pole. The passband bandwidth can be adjusted by adjusting the position of the transmission poles. Then the physical parameters of the designed filter are given. The simulated results of the designed filter are obtained. Finally, the designed filter is fabricated and measured. Simulations are basically consistent with the measured ones, which verify the correctness of the design theory.
近年来,随着无线通信技术的发展,多个通信标准的融合,双频带带通滤波器在GPS和北斗导航、WIFI通信、雷达监测等系统中具有十分广泛的应用.因此研究双频带带通滤波器具有重要的意义.使用双频带带通滤波器可以同时滤除2个频段内各种无用信号与噪声,降低频段之间的信号干扰,达到频谱资源的有效利用,同时减少滤波器的个数.近些年,双频带带通滤波器的研究也取得一定进展.李等[1]基于非对称阶梯阻抗谐振器,设计了带宽可调节的双频带带通滤波器法.张等[2]基于缺陷地结构设计了双频带带通滤波器,通过不同组合方式的双模开口谐振环产生2个通带. Wu等[3]在引入2个变容二极管之后,通过改变变容二极管的电容来改变四个谐振频率,可以独立地调谐2个通带带宽. Guo等[4]提出了一种新颖的紧凑型双频带滤波分频器,它是基于十字形谐振器设计的,兼有分频和滤波功能,从而实现了结构的紧凑性. Feng等[5]通过常规的耦合线和开路/短路枝节设计了双频带带阻滤波器,在通带内获得九个传输极点,可以灵活地调节双频带阻滤波器的2个中心频率.基于十字形谐振器,Bi等[6]构建具有固定和可重构带宽的双频带带通滤波器;Bi等[7]提出的十字形谐振器由一对带有短路端和开路端的并行耦合线组成,实现了2个具有相同纹波响应的通带.
笔者提出了一种基于不等长十字形谐振器的双频带带通滤波器.首先利用奇偶模电路分析法对其等效电路进行分析,得到等效电路的奇偶模输入阻抗以及传输零点和传输极点表达式;其次讨论了传输极点随着频率变化的规律;再次给出了滤波器结构的物理参数,将所提出的滤波器在HFSS软件上进行仿真优化;最后制作和测试了实物.测试结果和仿真结果呈现良好的一致性.笔者所提出的滤波器易于加工,没有金属过孔接地,理论分析简单,具有高选择性、低插入损耗等优点.
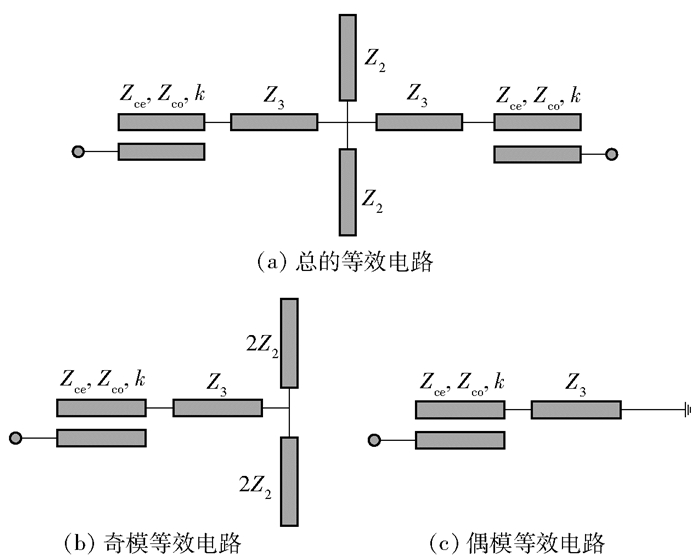
1 不等长十字形谐振器双频带带通滤波器等效电路分析图 1所示为不等长十字形谐振器双频带带通滤波器的等效电路,利用平行耦合线和不等长十字形谐振器结构组成了双频带带通滤波器.在等效电路中,平行耦合线的偶模阻抗为
|
图 1 不等长十字形谐振器双频带带通滤波器 |
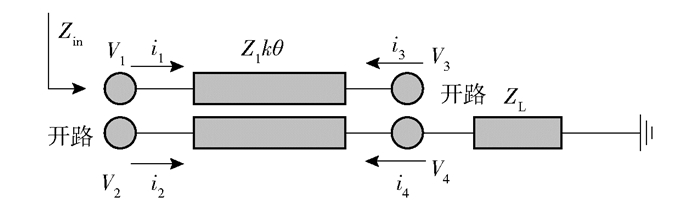
图 2所示为不等长十字形谐振器双频带带通滤波器总的等效电路.首先在图 1(b)和(c)中将传输线Z3及其后面部分看作是平行耦合线的负载ZL.因此,在推导奇偶模输入阻抗前,可先研究如图 2所示的带负载ZL的单端口输入阻抗,图 2中的平行耦合线四端口的电压和电流满足式(1a)和式(1b).
| $ \left[ {\begin{array}{*{20}{c}} {{v_1} - {v_2}}\\ {{i_1} - {i_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{j}}{Z_{{\rm{co}}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{\rm{j}}{Y_{{\rm{co}}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_4} - {v_3}}\\ { - ({i_4} - {i_3})} \end{array}} \right] $ | (1a) |
| $ \left[ {\begin{array}{*{20}{c}} {{v_1} + {v_2}}\\ {{i_1} + {i_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{j}}{Z_{{\rm{ce}}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{\rm{j}}{Y_{{\rm{ce}}}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_4} + {v_3}}\\ { - ({i_4} + {i_3})} \end{array}} \right] $ | (1b) |
|
图 2 带负载ZL的耦合线传输模型 |
其中:
| $ {z_{{\rm{in}}}} = \frac{{\sqrt {1 - {k^2}} {z_1}{z_{\rm{L}}}{\rm{tan}}(\theta ) + {\rm{j}}z_1^2[{k^2}{\rm{ta}}{{\rm{n}}^2}\theta - (1 - {k^2})]}}{{\sqrt {1 - {k^2}} {z_1}{\rm{tan}}\theta + {\rm{j}}(1 - {k^2}){z_{\rm{L}}}{\rm{ta}}{{\rm{n}}^2}\theta }} $ | (2) |
根据传输线理论可以得到奇模负载阻抗(zle)和偶模负载阻抗(zlo)的表达式为式(3)和式(4).将式(3)和(4)代入式(2)中,可以得到奇偶模输入阻抗表达式
| $ {{z_{{\rm{le}}}} = \frac{{{z_3}({z_2} - {z_3}{\rm{ta}}{{\rm{n}}^2}\theta )}}{{({z_3} + {z_2}){\rm{jtan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}} $ | (3) |
| $ {{z_{{\rm{lo}}}} = {z_3}{\rm{jtan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } $ | (4) |
对于对称互易二端口网络,归一化频率响应为
| $ {{s_{11}} = {s_{22}} = \frac{{{z_{{\rm{ ine }}}}{z_{{\rm{ ino }}}} - 1}}{{({z_{{\rm{ ine }}}} - 1)({z_{{\rm{ ino }}}} - 1)}}} $ | (5) |
| $ {{s_{12}} = {s_{21}} = \frac{{{z_{{\rm{ ine }}}} - {z_{{\rm{ ino }}}}}}{{({z_{{\rm{ ine }}}} - 1)({z_{{\rm{ ino }}}} - 1)}}} $ | (6) |
其中:zine为偶模输入阻抗,zino为奇模输入阻抗;滤波器的传输零点条件为zine=zino.利用式(2)可以得到
| $ {z_{{\rm{ ine (o)}}}} = \frac{{\sqrt {1 - {k^2}} {z_1}{z_{{\rm{ le (o)}}}} + {\rm{j}}z_1^2[{k^2}{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - (1 - {k^2}){\rm{cot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ]}}{{\sqrt {1 - {k^2}} {z_1} + {\rm{j}}(1 - {k^2}){z_{{\rm{ le (o)}}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }} $ | (7) |
由式(7)可知,当θ等于0°、180°、360°满足zine=zino,即滤波器结构在0、f0、2f0有固定的传输零点.
双频带带通滤波器的偶模谐振条件为zine=∞,可以得到式(8a),奇模谐振条件为zino=∞,可以得到式(8b),进而得到奇模传输极点式(9a)、式(9b)和偶模传输极点式(9c)和式(9d).
| $ \sqrt {1 - {k^2}} {z_1} - (1 - {k^2}){z_3}{\kern 1pt} {\rm{ta}}{{\rm{n}}^2}\theta = 0 $ | (8a) |
| $ \begin{array}{*{20}{c}} {\sqrt {1 - {k^2}} {z_1}({z_2} + {z_3}) + (1 - {k^2}){z_2}{z_3} - }\\ {(1 - {k^2})z_3^2{\kern 1pt} {\kern 1pt} {\rm{ta}}{{\rm{n}}^2}\theta = 0} \end{array} $ | (8b) |
| $ {{f_{{\rm{po1}}}} = \frac{{2{f_0}}}{\pi }{\rm{arctan}}\left( {\sqrt {{u_{{\rm{po}}}}} } \right)} $ | (9a) |
| $ {{f_{{\rm{po2}}}} = \frac{{2{f_0}}}{\pi }[\pi - {\rm{arctan}}(\sqrt {{u_{{\rm{po}}}}} )]} $ | (9b) |
| $ {{f_{{\rm{pe1}}}} = \frac{{2{f_0}}}{\pi }{\rm{arctan}}(\sqrt {{u_{{\rm{pe}}}}} )} $ | (9c) |
| $ {f_{{\rm{pe2}}}} = \frac{{2{f_0}}}{\pi }[\pi - {\rm{arctan}}(\sqrt {{u_{{\rm{pe}}}}} )] $ | (9d) |
| $ \begin{array}{l} {\rm{其中}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {u_{{\rm{po}}}} = \frac{{\sqrt {1 - {k^2}} {z_1}}}{{(1 - {k^2}){z_3}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {u_{{\rm{pe}}}} = \frac{{\sqrt {1 - {k^2}{z_1}} ({z_2} + {z_3}) + (1 - {k^2}){z_2}{z_3}}}{{(1 - {k^2}){z_3}}} \end{array} $ |
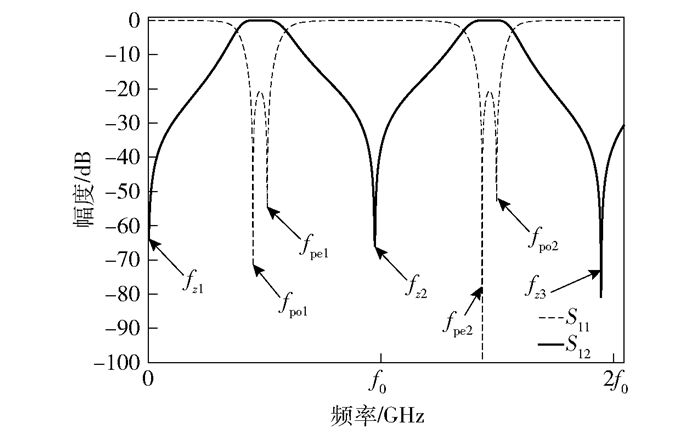
图 3给出了双频带带通滤波器等效电路的传输零点和传输极点分布情况.双频带带通滤波器有3个固定的传输零点fz1、fz2、fz3,分别在0、f0、2f0处,传输零点的位置与滤波器等效电路中的阻抗参数无关,只取决于电长度θ.双频带带通滤波器有4个传输极点fpo1、fpe1、fpo2、fpe2,第1个偶模传输极点和第1个奇模传输极点构成了第1个通带,剩下2个传输极点构成了第2个通带.与等长度终端短路的十字形带通滤波器相比较[8],笔者所提出的双频带带通滤波器传输极点要多1个,而且在4个传输极点中,两两靠近,可以实现双频带滤波器设计.
|
图 3 滤波器等效电路的零极点分布 |
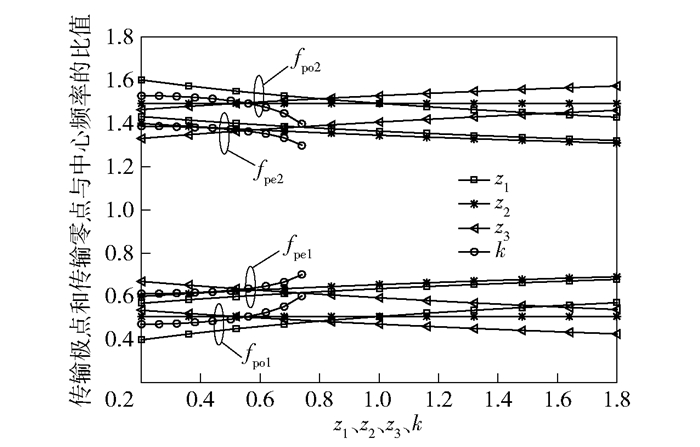
不等长十字形谐振器双频带带通滤波器的传输零点主要由电长度θ决定,滤波器的通带位置、带宽、插入损耗s21和回波损耗s11等特性主要由z1、z2、z3和k这4个参数决定. 图 4给出了归一化阻抗和耦合系数的不同取值对传输极点位置的影响.在实际滤波器设计中,根据所要设计的滤波器带宽,中心频率等要求,在图 4中选择相应的阻抗值和耦合系数,可得到由4个传输极点形成的2个通带.
|
图 4 参数z1~z3和k对fpo1/f0、fpo2/f0、fpe1/f0、fpo2/f0的影响 |
双频带带通滤波器在[0, 2f0]的频率范围内传输极点和传输零点的关系满足
| $ {f_{{{z1}}}} < {f_{{\rm{po1}}}} < {f_{{\rm{pe1}}}} < {f_{{\rm{z2}}}} < {f_{{\rm{pe2}}}} < {f_{{\rm{po2}}}} < {f_{{\rm{z3}}}} $ | (10) |
在选取等效电路归一化阻抗的初始参数为z1=1、z2=0.8、z3=1.3和k=0.6的情况下,图 4给出了z1、z2、z3和k对传输极点的影响.保持其他参数不变,随着z1值增大,2个通带内的2个传输极点间距都会减小,在z1大于1.2时,2个通带内的传输极点间距明显减小,表明当z1大于1.2时通带带宽变化较大.保持其他参数不变,随着z2值变大,奇模传输极点位置不变,2个偶模传输极点位置靠近中心频率f0,2个通带带宽增加.保持其他参数不变,随着z3的增加,2个通带内传输极点的间距有稍微的减小,但是对带宽影响不大.当k增加的时候,2个通带内的传输极点间距会减小,在大于0.6时通带内传输极点间距减小较快,同样对带宽的影响不明显.传输极点的位置也随着这4个参数的变化有不一样的趋势,可以通过调节这些参数来调节传输极点的位置,进而调节通带带宽,满足滤波器设计要求.
在滤波结构中,由于z1较小,而所要实现的耦合强度较高,考虑PCB板的加工精度,采用平行耦合线的办法达不到设计标准与要求.因此,借鉴学者许进所提出的三线耦合代替两线耦合的办法,提高耦合强度,满足设计要求[9].
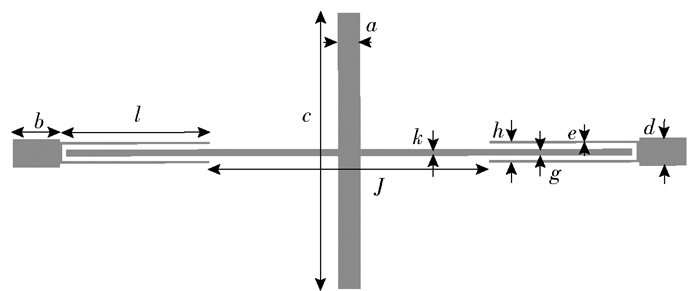
3 仿真与测试结果双频带通滤波器设计在Rogers RT5880印制电路板上, 介质板材料是聚四氟乙烯玻璃纤维增强材料,介电常数为2.2,损耗因子为0.000 9,介质板厚度是0.508 mm.根据选择的电路相对阻抗参数z1=1、z2=0.8、z3=1.3和耦合系数k=0.6,滤波器的最初物理结构参数可以通过ADS LineCalc计算得到.然后运用HFSS对双频带带通滤波器结构参数进行仿真优化,得到滤波器结构的最终物理参数,如图 5所示.滤波器的物理结构参数为:a=1.8 mm,b=5 mm,c=22.8 mm,d=1.54 mm,e=0.2 mm,g=0.4 mm,h=1.1 mm,j=24 mm,k=0.4 mm,l=13.4 mm.最后制作并且测试了双频带带通滤波器. 图 6为双频带带通滤波器的实物图. 图 7所示为双频带带通滤波器的仿真结果和测试结果.
|
图 5 不等长十字形谐振器双频带带通滤波器 |

|
图 6 双频带带通滤波器实物 |
|
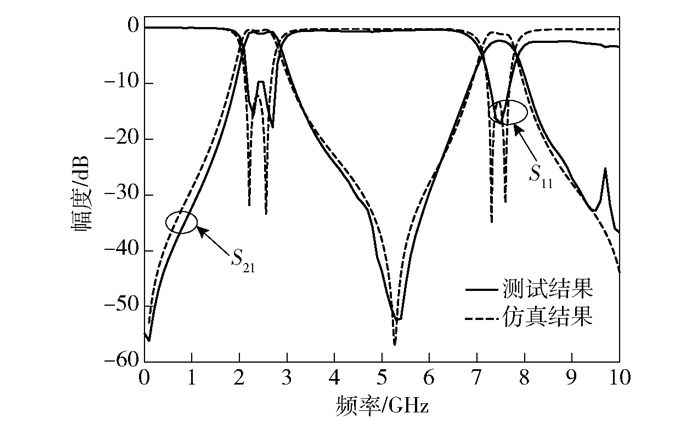
图 7 双频带带通滤波器仿真结果与实测结果 |
在图 7中,双频带带通滤波器的2个通带分别为2.2~2.7 GHz和7.2~7.6 GHz,通带内的回波损耗s11小于-10 dB,带外抑制良好,s21低于-20 dB.实测结果与仿真结果吻合较好,仿真结果和测试结果之间的误差主要归咎于加工误差,金属损耗和介质损耗以及SMA连接头等非理想因素.
与此同时,将笔者所设计的双频带带通滤波器与已有文献的双频带带通滤波器进行了比较,如表 1所示.在表 1中,文献[1]中描述的双频带带通滤波器带宽较小;文献[2]中描述的滤波器实测效果与仿真结果有较大差距,在实际工程应用中需要进一步改进.文献[6-7]中描述的双频带带通滤波器相对尺寸较大;笔者所提出的双频带带通滤波器等效电路简单,仿真结果与实测结果一致,同时电路尺寸较小,满足小型化要求.
|
|
表 1 双频带带通滤波器性能参数比较 |
笔者利用不等长十字形谐振器和耦合线结构组成双频带带通滤波器.然后运用奇偶模等效电路分析法对其进行分析,得到等效电路的奇偶模输入阻抗以及传输零点和传输极点表达式.对传输零点和传输极点进行了讨论分析,接着将等效电路参数转化成物理结构参数.在HFSS软件上对滤波器结构进行仿真优化,同时制作和测试了滤波器实物,仿真结果和实测结果呈现良好的一致性.滤波器的2个通带分别位于2.2~2.7 GHz和7.2~7.6 GHz,通带内的回波损耗小于-10 dB,带外抑制良好.与现有的同类双频带带通滤波器相比,所提出的滤波器尺寸小,仅为0.112λg×0.24λg,理论设计简单,并且在实际工程中易于制造,同时具有高选择性、低插入损耗等优点.设计双频带带通滤波器可以根据设备的实际需求,调整参数取值,得到无线通信系统不同要求的双频带带通滤波器, 因此可以广泛地应用于现代通信新系统中.
| [1] |
李学斌, 郭建卓, 韩宇南. 基于非对称SIR的小型化双频带带通滤波器设计[J]. 北京邮电大学学报, 2015, 38(2): 104-107. Li Xuebin, Guo Jianzhuo, Han Yunan. Compact dual band-pass filter design using asymmetrical stepped impedance resonators[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(2): 104-107. |
| [2] |
张洪欣, 张旭东, 贺鹏飞. 基于缺陷地结构的小型化双频带带通滤波器[J]. 电波科学学报, 2016, 31(2): 363-367. Zhang Hongxin, Zhang Xudong, He Pengfei. Miniaturized dual-band band-pass filter using defect ground structure[J]. The Chinese Journal of Radio Science, 2016, 31(2): 363-367. |
| [3] |
Wu Yongle, Nan Lixia, Jiao Lingxiao, et al. Dual-band coupled-line band-pass filter with independently tunable bandwidths[J]. China Communications, 2016, 13(9): 60-64. DOI:10.1109/CC.2016.7582297 |
| [4] |
Guo Qingyi, Zhang Xiuyin, Gao Li, et al. Novel compact planar crossover with bandpass response based on cross-shaped resonator[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2017, 7(12): 2018-2026. DOI:10.1109/TCPMT.2017.2739241 |
| [5] |
Feng Wenjie, Hong Meiling, Che Wenquan, et al. Dual-band microstrip band-stop filter with multiple transmission poles using coupled lines[J]. IEEE Microwave and Wireless Components Letters, 2017, 27(3): 236-238. DOI:10.1109/LMWC.2017.2661704 |
| [6] |
Bi Xiaokun, Cheng Teng, Cheong P, et al. Design of dual-band band-pass filters with fixed and reconflgurable bandwidths based on terminated cross-shaped resonators[J]. IEEE Transactions on Circuits and Systems-Ⅱ:Express Briefs, 2019, 66: 317-321. DOI:10.1109/TCSII.2018.2848667 |
| [7] |
Bi Xiaokun, Zhang Xiao, Wong S W, et al. Design of equal-ripple dual-wideband bandpass filter with minimum design parameters based on cross-shaped resonator[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2020, 67(10): 1780-1784. DOI:10.1109/TCSII.2019.2951781 |
| [8] |
Wang Hui, Yang Guo, Kang Wei. Application of cross-shaped resonator to the ultra wideband bandpass filter design[J]. IEEE Microwave and Wireless Components Letters, 2011, 17(12): 667-669. |
| [9] |
许进.多模谐振器宽带与多频带带通滤波器的研究与设计[D].南京: 南京理工大学, 2013.
|


