2. 空军工程大学 防空反导学院, 西安 710051
三维旋转不变子空间(3D-ESPRIT)算法估计三维几何绕射理论(GTD)的散射中心模型时,参数精度不高,噪声鲁棒性较差,为此,提出一种改进的3D-ESPRIT算法.通过构建原始回波数据的共轭矩阵、对协方差矩阵叠加、取平均、平方处理,可提高对目标原始回波数据的利用率,并增大信号特征值与噪声特征值之间的差距,增大了信噪比,从而提高参数的估计精度.基于不同算法估计得到的三维GTD模型参数,比较了不同算法估计的参数均方差.仿真结果表明,改进算法的参数估计性能及噪声鲁棒性均优于经典3D-ESPRIT算法和改进的免配对3D-ESPRIT算法.
2. Air and Missile Defense College of Air Force Engineering University, Xi'an 710051, China
The noise robustness and parameter estimation performance of the classical three-dimensional estimating signal parameter via rotational invariance techniques (3D-ESPRIT) algorithm are poor when estimating parameters of the three dimensional geometric theory of diffraction(3D-GTD) model at low signal-to-noise ratio (SNR). To solve this problem, a modified algorithm is proposed. The modified algorithm improves the parameter estimation accuracy by constructing conjugated matrix of the original back-scattered data, averaging the covariance matrices and performing quadratic power on the total covariance matrix to get another novel covariance matrix. The modified algorithm can broaden the differences between the eigenvalues of noises and signals, which is equivalent to increase SNR. Based on the parameters estimated by different algorithms, root-mean-square-errors of different parameters can be compared. Simulations verify that the parameter estimation performance and noise robustness of the modified algorithm are better than the classical 3D-ESPRIT algorithm and the improved algorithm without pair.
在高频区,雷达目标的后向电磁散射回波可视为有限个强散射点的相干叠加,而这些强散射点通常可称为雷达目标的散射中心[1].而通过构建合理近精准的散射中心模型,可更有效地描述目标的散射特性,对深入研究其散射机理起到重要的作用.目前,基于几何绕射理论的(GTD,geometric theory of diffraction)散射中心模型[1]对目标在高频区散射特性的刻画最为准确.而如何准确地从雷达回波数据提取出目标的散射中心模型参数成为研究热点.目前存在的主流算法有多重信号分类(MUSIC,multiple signal classification)算法[2-7]、旋转不变子空间(ESPRIT,estimating signal parameter via rotational invariance techniques)算法[8-15]、增广矩阵束(MEMP,matrix enhancement matrix pencil)[16]算法等,通过上述算法即可对GTD散射中心模型进行参数估计提取.
利用三维GTD模型对雷达目标的电磁散射数据进行描述.针对经典3D-ESPRIT算法存在的参数失配问题,王菁[15]提出一种改进的免配对3D-ESPRIT算法,有效解决了参数失配问题,但在信噪比情况下,改进免配对3D-ESPRIT算法的参数估计较低.为解决免配对3D-ESPRIT算法在低信噪比时,参数估计精度降低、算法鲁棒性较差这一问题,在免配对3D-ESPRIT算法的基础上,笔者提出了一种改进的3D-ESPRIT算法.改进算法通过构建原始回波数据的共轭矩阵、对协方差矩阵叠加、取平均、平方处理,提高了雷达目标原始回波数据的利用率,从而有效地提高了算法的参数估计性能和噪声鲁棒性.
1 信号模型GTD模型作为一种经典的散射中心模型,可有效描述雷达目标在高频区的电磁后向散射特性,以步进频率雷达信号为例,目标的三维GTD模型可表示为
| $ \begin{array}{*{20}{c}} {E({f_m},{\theta _n},{\varphi _k}) = }\\ {\sum\limits_{i = 1}^I {{A_i}} {{\left( {{\rm{j}}\frac{{{f_m}}}{f}} \right)}^{{\alpha _i}}}{\rm{exp}}[ - 4\pi {\rm{j}}{f_m}({x_i}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + }\\ {{y_i}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + {z_i}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi )/c] + \omega ({f_m},{\theta _n},{\varphi _k})} \end{array} $ | (1) |
其中:E(fm, θn, φk)表示目标的后向散射回波,I代表散射中心个数,{Ai, αi, xi, yi, zi}分别表示第i个散射中心的散射强度、散射类型、横向距离、纵向距离及垂直距离. fm=f0+mΔf,其中f0为起始频率,Δf为步进频率,m代表频率下标;θn=θ0+nΔθ,n=0, 1, …, N,其中θ0为起始方位角,Δθ为步进方位角,n为方位角下标;θn=θ0+nΔθn=0, 1, …, N,其中φ0为起始俯仰角,Δφ为步进俯仰角,k为俯仰角下标,φk=φ0+kΔφ,k=0, 1, …, K;nΔθ、kΔφ分别为方位方向上的小转角、俯仰方向上的小转角. c=3×108 m/s为电磁波传播速度,ω(fm, θn, φk)为复高斯白噪声. αi为0.5的整数倍,共有5种[1].式(1)中的{Ai, αi, xi, yi, zi}即为待估计散射中心参数.
2 改进算法原理针对经典3D-ESPRIT算法在信噪比较低时参数估计性能下降这一问题,提出了一种改进的3D-ESPRIT算法,有效提高了算法的噪声鲁棒性与参数估计性能.改进算法主要对经典3D-ESPRIT算法前2个步骤进行改进,具体改进步骤如下.
步骤1 定义大小为PQL×PQL的置换矩阵J:
| $ \mathit{\boldsymbol{J}} = {\left[ {\begin{array}{*{20}{c}} 0& \cdots &0&1\\ \vdots &0&1&0\\ 0& {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} & \ddots & \vdots \\ 1&0& \cdots &0 \end{array}} \right]_{PQL \times PQL}} $ | (2) |
其中:M/2≤P≤2M/3,N/2≤Q≤2N/3,K/2≤L≤2K/3.
基于式(2),可得到包含目标回波数据共轭数据信息的矩阵为
| $ {\mathit{\boldsymbol{E}}_{{\rm{conj}}}}{\rm{ }} = \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{X}}^x} $ | (3) |
其中
| $ {\mathit{\boldsymbol{X}}^x} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}_0^x}&{\mathit{\boldsymbol{X}}_1^x}& \cdots &{\mathit{\boldsymbol{X}}_{M - P}^x}\\ {\mathit{\boldsymbol{X}}_1^x}&{\mathit{\boldsymbol{X}}_2^x}& \cdots &{\mathit{\boldsymbol{X}}_{M - P + 1}^x}\\ \vdots & \vdots & \cdots & \vdots \\ {\mathit{\boldsymbol{X}}_{P - 1}^x}&{\mathit{\boldsymbol{X}}_P^x}& \cdots &{\mathit{\boldsymbol{X}}_{M - 1}^x} \end{array}} \right] $ | (4) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{X}}_m^x = \\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}(m,0)}&{\mathit{\boldsymbol{x}}(m,1)}& \cdots &{\mathit{\boldsymbol{x}}(m,K - L)}\\ {\mathit{\boldsymbol{x}}(m,1)}&{\mathit{\boldsymbol{x}}(m,2)}& \cdots &{\mathit{\boldsymbol{x}}(m,K - L + 1)}\\ \vdots & \vdots & \cdots & \vdots \\ {\mathit{\boldsymbol{x}}(m,L - 1)}&{\mathit{\boldsymbol{x}}(m,L)}& \cdots &{\mathit{\boldsymbol{x}}(m,K - 1)} \end{array}} \right] \end{array} $ | (5) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{x}}(m,k) = \\ \left[ {\begin{array}{*{20}{c}} {E(m,0,k)}&{E(m,1,k)}& \cdots &{E(m,N - Q,k)}\\ {E(m,1,k)}&{E(m,2,k)}& \cdots &{E(m,N - Q + 1,k)}\\ \vdots & \vdots & \cdots & \vdots \\ {E(m,Q - 1,k)}&{E(m,Q,k)}& \cdots &{E(m,N - 1,k)} \end{array}} \right] \end{array} $ | (6) |
通过对新得到的矩阵Econj及原目标回波数据矩阵Xx的自相关矩阵相加,并作取平均处理,可得到一个新的总协方差矩阵R:
| $ \mathit{\boldsymbol{R}} = \frac{{{\mathit{\boldsymbol{X}}^x}{{({\mathit{\boldsymbol{X}}^x})}^{\rm{H}}} + {E_{{\rm{conj}}}}{{({E_{{\rm{conj}}}})}^{\rm{H}}}}}{2} $ | (7) |
步骤2 式(7)得到的新总协方差矩阵为Hermittan矩阵,因此其满足R=RH,即R1=RRH=R2,则矩阵R1、R两者的特征值与特征向量具有以下关系:
| $ \left. {\begin{array}{*{20}{l}} {{\lambda _1} = {\lambda ^2}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \end{array}} \right\} $ | (8) |
其中:λ1、λ分别代表矩阵R1和R的特征值,Λ1、Λ分别代表矩阵R1和R的特征向量.
用R1代替R,可增大信号特征值与噪声特征值之间的差距,并且不会改变原有的特征向量,因此在信噪比较低时,更容易区分信号特征值和噪声特征值.构造下式:
| $ {\mathit{\boldsymbol{R}}_1} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{R}}^{\rm{H}}} = {\mathit{\boldsymbol{R}}^2} $ | (9) |
对新的总协方差矩阵R1 3D-ESPRIT算法的三维GTD模型参数估计提取步骤,即可得到三维GTD模型中的各参数值.
提出的算法主要针对经典3D-ESPRIT算法中的前2个步骤,即协方差矩阵的构造作改进.因此,仅对2种算法的协方差矩阵构造这一步骤的运算量作比较分析,经典3D-ESPRIT算法在协方差矩阵构造这一步的运算量为P2Q2L2(M-P+1)(N-Q+1)(K-L+1),而提出的改进3D-ESPRIT算法在此步骤的运算量为P2Q2L2[3(M-P+1)(N-Q+1)(K-L+1)+2PQL+1].由此可见,改进算法在构造协方差矩阵这一步的运算量要稍大于经典3D-ESPRIT算法.
3 仿真实验假设目标由4个散射中心构成,具体的参数设置见表 1.仿真实验设定雷达的初始工作频率f0为10 GHz,频率步进为16 MHz,总频率步进数M=11;初始方位角θ0、初始俯仰角φ0均为90°,角度间隔均为0.01°,总方位角度数N=11,总俯仰角度数K=11. 4个时散射中心的各模型参数见表 1.在回波数据中加入-10~20 dB的信噪比(SNR,signal-to -noise ratio),SNR定义为
| $ S = 10{\rm{lg}}\left( {\frac{{\sigma _n^2}}{{\sigma _s^2}}} \right) $ | (10) |
|
|
表 1 散射中心参数 |
其中
分别在-10~20 dB信噪比条件下进行200次蒙特卡洛实验,并比较不同算法估计得到参数的均方差(RMSE,root-mean-errors),仿真结果如图 1~图 5所示.定义均方差RMSE为
| $ E(z) = \sqrt {\frac{{\sum\limits_{i = 1}^D {{{({z_i} - z)}^2}} }}{D}} $ | (11) |
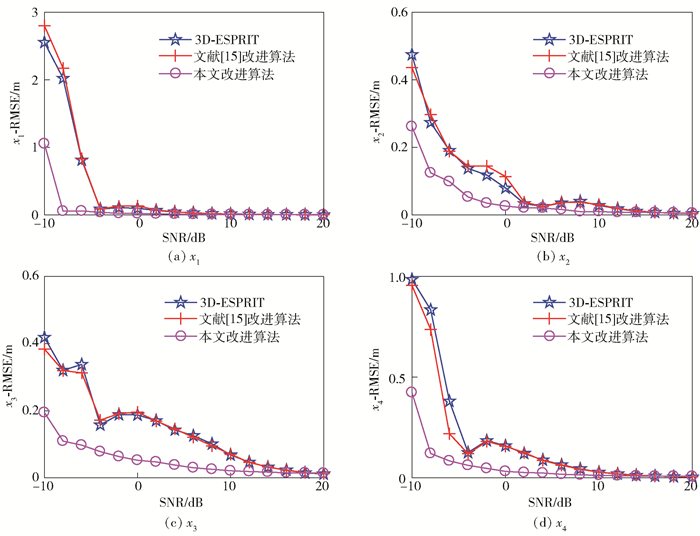
|
图 1 x1~x4的均方差比较 |
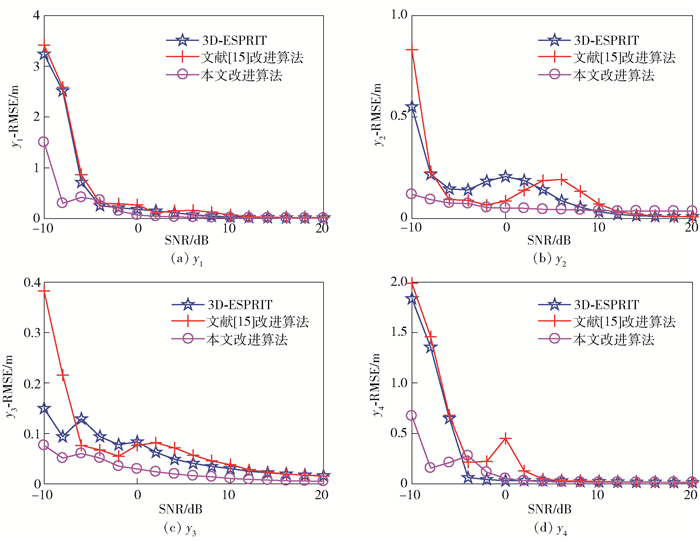
|
图 2 y1~y4的均方差比较 |
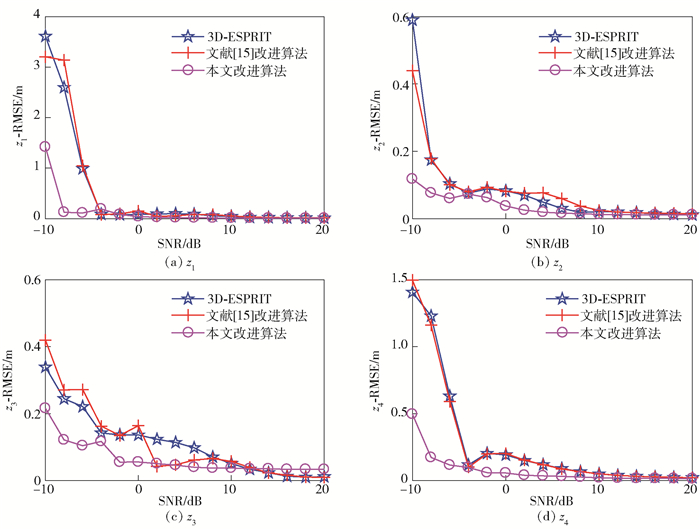
|
图 3 z1~z4的均方差比较 |
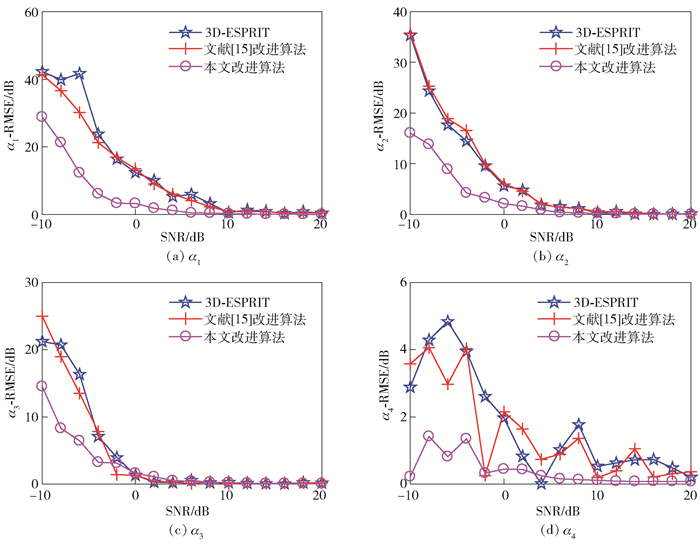
|
图 4 α1~α4的均方差比较 |
|
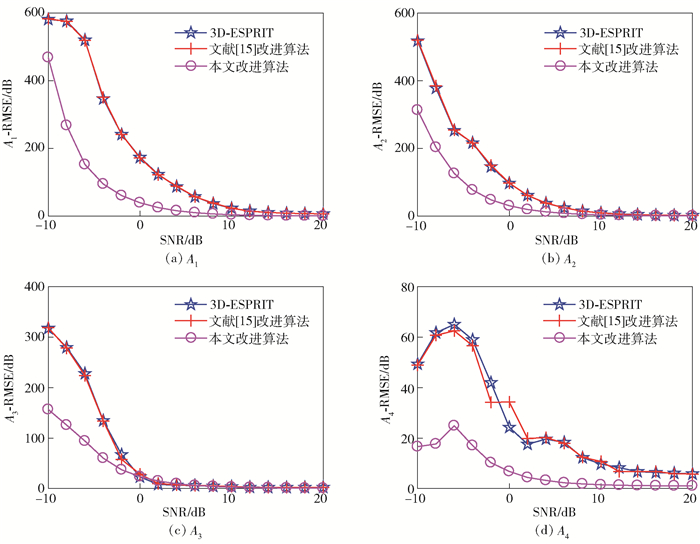
图 5 A1~A4的均方差比较 |
其中:zi为估计参数,z为设定参数,D为蒙特卡洛次数.
由图 1~图 5可知,改进的3D-ESPRIT算法估计得到的各散射中心模型参数的均方差均小于经典3D-ESPRIT算法及文献[15]中的改进算法.可以发现,在信噪比为-10~0 dB的仿真条件下,改进的算法优势更为明显,因此可以验证,通过增大原始回波数据的利用率及对总协方差矩阵取平方处理的方法,能有效提高算法的噪声鲁棒性和参数估计性能.
4 结束语笔者提出了一种改进3D-ESPRIT算法,该算法不仅解决了参数失配问题,而且在低信噪比的条件下参数估计性能更优,噪声鲁棒性更加稳定.所提算法在运算复杂度增加不大的条件下,解决了传统旋转不变子空间算法低信噪比时参数估计精度较低这一问题.仿真实验验证了改进算法在估计三维GTD模型参数过程中的先进性和有效性.相比于经典3D-ESPRIT算法,提出的改进算法的运算量稍有增加,因此,如何提出快速的散射中心模型参数估计算法将是此领域的重点研究方向.
| [1] |
Potter L C, Chiang Daming, Carriere R, et al. A GTD-based parametric model for radar scattering[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1058-1067. DOI:10.1109/8.467641 |
| [2] |
贺治华, 黎湘, 张旭峰, 等. 基于MUSIC算法的GTD模型参数估计[J]. 系统工程与电子技术, 2005, 27(10): 1685-1688. He Zhihua, Li Xiang, Zhang Xufeng, et al. MUSIC-based parametric estimation of GTD model[J]. Systems Engineering and Electronics, 2005, 27(10): 1685-1688. |
| [3] |
郑舒予, 张小宽, 郭艺夺, 等.一维GTD散射中心模型参数估计的改进MUSIC算法[J/OL].北京航空航天大学学报, 2020[2020-07-11]. https://doi.org/10.13700/j.bh.1001-5965.2019.0556. Zheng Shuyu, Zhang Xiaokuan, Guo Yiduo, et al. Parameter estimation of the 1D-GTD scattering center model based on an improved MUSIC algorithm[J/OL]. Journal of Beijing University of Aeronautics and Astronautics, 2020[2020-07-11]. https://doi.org/10.13700/j.bh.1001-5965.2019.0556. |
| [4] |
邱志强.基于空间谱估计的雷达目标散射中心提取研究[D].成都: 电子科技大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10614-1016162043.htm
|
| [5] |
刘寅生, 段洪涛, 范振雄, 等. 基于改进MUSIC算法的短波非规则天线阵列测向系统[J]. 北京邮电大学学报, 2019, 42(5): 42-47. Liu Yinsheng, Duan Hongtao, Fan Zhenxiong, et al. Improved MUSIC algorithm for HF direction finding system with non-regular antenna array[J]. Journal of Beijing University of Posts and Telecommunications, 2019, 42(5): 42-47. |
| [6] |
Kintz A L, Gupta I J. A modified MUSIC algorithm for direction of arrival estimation in the presence of antenna array manifold mismatch[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(11): 4836-4847. DOI:10.1109/TAP.2016.2600700 |
| [7] |
郑舒予, 张小宽, 宗彬锋. 基于改进MUSIC算法的散射中心参数提取及RCS重构[J]. 系统工程与电子技术, 2020, 42(1): 76-82. Zheng Shuyu, Zhang Xiaokuan, Zong Binfeng. Extraction of scattering center parameters and reconstruction of RCS based on improved MUSIC algorithm[J]. Systems Engineering and Electronics, 2020, 42(1): 76-82. |
| [8] |
Zheng Shuyu, Zhang Xiaokuan, Zong Binfeng, et al. Parameter estimation of the 2D-GTD model and RCS reconstruction based on an improved 2D-ESPRIT algorithm[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2020, 30(7): 1-11. |
| [9] |
Sahnoun S, Usevich K, Comon P. Multidimensional ESPRIT for damped and undamped signals:algorithm, computations, and perturbation analysis[J]. IEEE Transactions on Signal Processing, 2017, 65(22): 5897-5910. DOI:10.1109/TSP.2017.2736512 |
| [10] |
Zheng Wang, Zhang Xiaofei, Sun Huapu, et al. Non-circular generalised-ESPRIT algorithm for direction of arrival estimation[J]. IET Radar, Sonar & Navigation, 2017, 11(5): 736-744. |
| [11] |
Rouquette S, Najim M. Estimation of frequencies and damping factors by two-dimensional ESPRIT type methods[J]. IEEE Transactions on Signal Processing, 2001, 49(1): 237-245. |
| [12] |
Chen Xuan, Wan Baoquan, Zhao Tao, et al. Parameter estimation of three-dimensional scattering centers based on state space and ESPRIT method[J]. Procedia Computer Science, 2019, 147: 435-440. DOI:10.1016/j.procs.2019.01.261 |
| [13] |
Zheng Shuyu, Zhang Xiaokuan, Zong Binfeng, et al. GTD model parameters estimation based on improved LS-ESPRIT algorithm[C]//2019 Photonics & Electromagnetics Research Symposium-Fall (PIERS-Fall). Xiamen: IEEE Press, 2019: 2282-2289.
|
| [14] |
温晓杨, 石志广, 赵宏钟, 等. 一种基于3D-ESPRIT的散射中心参数估计算法[J]. 雷达科学与技术, 2007, 5(2): 118-123. Wen Xiaoyang, Shi Zhiguang, Zhao Hongzhong, et al. A 3D-ESPRIT method for radar target scattering centers parameters estimation[J]. Radar Science and Technology, 2007, 5(2): 118-123. |
| [15] |
王菁.光学区雷达目标散射中心提取及其应用研究[D].南京: 南京航空航天大学, 2010. http://cdmd.cnki.com.cn/article/cdmd-10287-1011291532.htm
|
| [16] |
Li Haiwen, Zhang Long, Jiang Chunqi, et al. Joint TOA and DOA estimation based on improved matrix pencil method[C]//2018 IEEE 4th International Conference on Computer and Communications (ICCC). Chengdu: IEEE Press, 2018: 763-768.
|



