2. 北京材料基因工程高精尖创新中心, 北京 100083
为优化移动通信网络的覆盖性能,针对天线指向变量中方位角与下倾角的内在关联性,提出了四元数域粒子群优化算法.该算法利用四元数表示天线指向,并基于四元数域乘法所表示的旋转实现粒子群算法的可行解沿最短路径进行更新.由于四元数域乘法不符合交换律,故在无穷小移动的概念上进一步提出了调和四元数粒子群优化算法,使粒子群中可行解的更新与惯性速度、朝向个体历史最优解和全局最优解的移动次序无关.实验结果表明,提出的两类算法,特别是调和算法在收敛速度和覆盖性能上均优于经典粒子群算法、萤火虫算法和遗传算法.
2. Beijing Advanced Innovation Center for Materials Genome Engineering, Beijing 100083, China
Aiming at the inherent correlation of azimuths and tilts of the antennas installed on the base stations, a quaternion-based particle swarm optimization algorithms is proposed to optimize the coverage performance for mobile networks, in which the quaternions represents the antenna orientations, and the rotations formed by the multiplication in the quaternion field ensures that the feasible solutions, that is the particles, update along the shortest paths. Moreover, the author considers the process to perform infinitesimal movements towards different directions in turn and thus introduced a blending quaternion-based particle swarm optimization algorithm to overcome the problems that the destination of the particle movement depends upon the order of directions including along the inertial velocity, towards the individual historical optimal solution and towards the global optimal solution, which is indeed caused by the anti-commutative law of quaternions. Simulations show that the proposed algorithms, especially the latter, perform better than the canonical particle swarm algorithm, firefly algorithm and genetic algorithm both in the convergence efficiency and the final optimized coverage.
随着虚拟现实、增强现实、车联网、超高清视频、智能家居等多样的新兴业务出现和海量终端设备的大规模联网,移动通信网络业务即将迎来爆发性增长.多样性的业务需求和数量庞大的终端接入将对移动通信网络的覆盖和容量等性能指标提出更高的要求,网络管理者和运营商必须面对和更好地解决网络覆盖和容量优化(CCO,coverage and capacity optimization)问题[1-2].
第5代移动通信系统(5G,the 5th generation of mobile communications system)已进入商用,后5G和第6代移动通信系统的研究方兴未艾.未来基站的分布将更加密集,射频传播受环境的影响更加复杂.同时,密集而复杂的基站部署将导致CCO问题的可调参数数量庞大,其中主要的可调参数包含无线信号发射功率、发射频率和基站天线的方位角、下倾角、挂高等资源分配参数.在某些给定的假设下,CCO问题已经被证明是一类非确定多项式难题(NP-Hard,non-deterministic polynomial hard).因此,未来移动通信网络的CCO问题将存在更大的挑战.
为了解决CCO的覆盖优化问题,学术和工业界提出了相对丰富的解决方案.近年来,移动通信网络覆盖优化算法主要包括基于学习的方法和基于群体智能的方法两大研究方向.前者旨在解决网络动态的自组织自优化问题,主要过程是学习具有不确定性的系统参数,分类相关问题,预测未来结果并探索潜在的解决方案.机器学习(ML,machine learning)[3],序列学习(SL,sequential learning)[4]和增强学习(RL,reinforcement learning)[5]被证明是有效的处理大量可配置数据并获得近似最优的解决方案.然而这些方法也存在局限,如需要大量的训练数据集、对不完整信息的计算复杂性和达到稳态所需要的计算开销十分巨大.基于群体智能的算法通过向自然界中某些生命现象或自然现象学习,利用某种机制指导种群对解空间进行搜索,实现对问题的求解,这类算法具有的自组织、自学习和自适应等特点[6],已被灵活应用在移动通信网络的覆盖率优化问题中.其中,粒子群算法(PSO,particle swarm optimization)[7],萤火虫算法(FFA,firefly algorithm)[8],遗传算法(GA,genetic algorithm)[9]等已被广泛用来优化多种网络场景覆盖率.通常,群体智能算法有利于获得全局最优解或近似最优解,但由于依赖群体计算,每个个体每次迭代都需要相当规模的计算复杂度[10].
在已有的通过调整天线角度的覆盖优化研究中,通常将天线的方位角和下倾角作为2个独立的变量讨论而忽略了其内在关联性[11],或者仅考虑天线的方位角或下倾角中的某一个变量[5, 7].事实上,这2个变量是一个整体且共同组成了天线指向变量;而联合调整天线指向变量和分别考虑2个变量的搜索效率将明显不同.因此,笔者将天线的方位角和下倾角变量从实数域映射到四元数域,实现了天线方位角和下倾角的联合调整,提出了四元数直接拓展的PSO(QPSO,quaternion-based PSO)算法解决复杂的覆盖率优化问题,其中四元数乘积表示旋转确保了粒子位置沿最短路径进行更新;另外,针对四元数乘积的不可交换性,提出四元数调和拓展的QPSO算法(BQPSO,blending QPSO);实验结果表明,提出的2种算法在网络覆盖率优化过程中非常高效,不仅算法的收敛速度相对于经典算法得到提升,而且最终的网络覆盖性能也优于经典的粒子群算法、萤火虫算法和遗传算法.
1 系统模型在给定区域D内, 设基站集合为{1, 2, …, Nb}, 其中第i个基站可表示为Bi.设每个基站都配有n根天线,Aij表示Bi上的第j根天线.所有天线的方位角和下倾角参数构成的序列表示为{α11, τ11, …αij, τij, …αNbn, τNbn}.
待测区域D中的均匀采样点集合可表示为γ={1, 2, …, Np},∀s∈γ.令pij(s)为从天线Aij发射到s的信号功率,在s处的信号干扰加上噪声比(SINR,signal to interference plus noise ratio)值可表示为
| $ \chi (s) = \frac{{\mathop {{\rm{max}}}\limits_{i,j} {p_{ij}}(s)}}{{{\sigma ^2} + \sum\limits_{i = 1}^{{N_{\rm{b}}}} {\sum\limits_{j = 1}^n {{p_{ij}}} } (s) - \mathop {{\rm{max}}}\limits_{i,j} {p_{ij}}(s)}} $ | (1) |
其中σ2是加性高斯白噪声(AWGN,additive white Gaussian noise)的方差.
在s处的覆盖状态c(s)由SINR值确定,即
| $ c(s) = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{ 若 }}\chi (s) \ge \lambda }\\ {0,}&{{\rm{ else }}} \end{array}} \right. $ | (2) |
其中λ表示SINR的阈值.该条件说明当s的SINR大于给定阈值时,该位置才会被移动通信网络所覆盖.
式(1)中的pij(s)由以下公式得出
| $ {p_{ij}}(s) = {p_{{\rm{tx}}}} + {G_{ij,s}} + {G_{\rm{r}}} - {T_{ij,s}} - {o_{{\rm{sf}}}} $ | (3) |
其中:ptx为天线的发射功率;Gij, s为Aij到采样点的天线增益,增益计算可表示为Gij, s=G(αij, τij)[6];Gr为接收端的天线增益;Tij, s为Aij到s的路径损耗;οsf是阴影衰落余量[12].
理论上,对给定区域D的覆盖率应表示为信号质量超过给定的SINR阈值的面积与总面积的比值.利用采样点可将覆盖率的评估近似表示为
| $ f({\alpha _{11}},{\tau _{11}}, \cdots ,{\alpha _{ij}},{\tau _{ij}}, \cdots ,{\alpha _{{N_{\rm{b}}}n}},{\tau _{{N_{\rm{b}}}n}}) \approx \frac{{\sum\limits_{s = 1}^{{N_{\rm{p}}}} c (s)}}{{{N_{\rm{p}}}}} $ | (4) |
其中c(s)即第s个采样点的覆盖状态.
在天线的指向变量中,下倾角根据工程需求存在一定的限制范围,而方位角存在周期性,故通常限制在一个周期内.
综合上述分析,为提高给定区域D内的覆盖性能,优化问题可表示为
| $ \begin{array}{*{20}{c}} {{\rm{max}}f({\alpha _{11}},{\tau _{11}}, \cdots ,{\alpha _{ij}},{\tau _{ij}}, \cdots ,{\alpha _{{N_{\rm{b}}}n}},{\tau _{{N_{\rm{b}}}n}})}\\ {{\rm{s}}{\rm{. t}}{\rm{. }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \pi < {\alpha _{ij}} \le \pi }\\ {L \le {\tau _{ij}} \le U,i = 1, \cdots ,{N_b},j = 1,2, \cdots ,n} \end{array} $ | (5) |
其中L和U分别表示下倾角的下限和上限,且L和U均在
下面首先引出经典PSO的覆盖率优化方法;然后,针对方位角和下倾角的特殊性和内在联系,将天线指向从实数域映射到四元数域;接着,提出了四元数域的PSO优化算法;最后,为解决四元数旋转的不可交换性,提出四元数域调和PSO优化算法.
在PSO中,将每个粒子定义为K维空间中问题的解.令xt表示粒子t的当前位置,此位置认为是每次迭代中对应优化问题的一个可行解,到目前为止最好的可行解的第k维表示为pt(k),所有粒子迄今最好的解记为g(k).粒子将在解空间内搜索最优解,一种经典PSO的粒子的速度和位置更新分别为
| $ \begin{array}{*{20}{c}} {v_t^{(k)}(n + 1) = }\\ {\kappa [v_t^{(k)}(n) + {r_1}{\delta _1}(p_t^{(k)} - x_t^{(k)}) + {r_2}{\delta _2}({g^{(k)}} - x_t^{(k)})]} \end{array} $ | (6) |
| $ x_t^{(k)}(n + 1) = x_t^{(k)}(n) + v_t^{(k)}(n + 1) $ | (7) |
其中r1和r2均取自[0, 1]的随机数.可令κ=
天线的指向变量在目标函数优化中具有以下特点:由于天线指向变量在球面解空间进行搜索时,从当前位置向目标位置移动存在多条路径.天线指向变量的变化本质上是一种旋转,而四元数非常适合表达三维的角度和旋转.因此可把天线的指向变量从实数域R2映射到四元数域Q.
假设α和τ分别表示一根天线的方位角和下倾角,用纯单位四元数q表示该天线的指向变量.从实数域到四元数域的映射可表示为
| $ \varphi :(\alpha ,\tau )\quad q = {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau {\rm{i}} + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau {\rm{j}} + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau {\rm{k}} $ | (8) |
因此,建立了从实数天线角度(α, τ)到纯单位四元数q的单射.
令q={q1, q2, …, qNbn}, q⊆Q,表示所有天线指向对应的纯单位四元数构成的向量,该向量中的元素qij=φ(αij, τij),因此,式(5)的优化目标转为
| $ {\rm{max}}f[{\varphi ^{ - 1}}({q_1}),{\varphi ^{ - 1}}({q_2}), \cdots ,{\varphi ^{ - 1}}({q_{{N_{\rm{b}}}n}}) $ | (9) |
其中φ-1(·)得到的方位角和下倾角应满足式(5)的约束.
2.2 四元数域PSO算法在四元数域对经典PSO算法进行拓展,通过式(8)将天线指向变量映射到四元数域,此时粒子群的任一粒子xt,个体最佳pt和全局最佳g均由四元数表示.粒子xt的第l维惯性旋转定义为
| $ V:v_t^{(l)}(n) $ | (10) |
为了接近个体最优值,朝向个体最优参数的旋转定义为
| $ {\rm{P}}:{\{ p_t^{(l)}{[x_t^{(l)}(n)]^{ - 1}}\} ^{{r_1}{\delta _1}}} $ | (11) |
类似地,为了接近全局最佳值,朝向全局最优参数的旋转定义为
| $ {\rm{G}}:{\{ {g^{(l)}}{[x_t^{(l)}(n)]^{ - 1}}\} ^{{r_2}{\delta _2}}} $ | (12) |
由于四元数乘法不满足交换律,粒子位置更新时的旋转次序将会对最终的结果产生不同的影响,即粒子从当前位置先朝个体最佳旋转,再朝全局最佳旋转,或者先朝全局最佳再朝个体最佳旋转,结果并不相同.粒子的旋转可依据以上3种定义实现,且共有6种不同的旋转更新方式,将不同的旋转组合简写为集合w={VPG, VGP, GPV, PGV, PVG, GVP}.根据四元数表示旋转计算的规则[14],以w中的VPG为例,粒子的速度更新公式为
| $ \begin{array}{*{20}{c}} {v_t^{(l)}(n + 1) = }\\ {(v_t^{(l)}(n){{\{ p_t^{(l)}{{[x_t^{(l)}(n)]}^{ - 1}}\} }^{{r_1}{\delta _1}}} \times }\\ {{{\{ {g^{(l)}}{{[x_t^{(l)}(n)]}^{ - 1}}\} }^{{r_2}{\delta _2}}}{)^{\kappa /2}}} \end{array} $ | (13) |
位置更新公式为
| $ x_t^{(l)}(n + 1) = v_t^{(l)}(n + 1)x_t^{(l)}(n){[v_t^{(l)}(n + 1)]^{ - 1}} $ | (14) |
其中:xt(l)为纯单位四元数,对应上文中的天线指向变量;vt(l)为单位四元数,对应天线指向的旋转.
基于四元数PSO的覆盖率优化表示为QPSO,为了区分四元数旋转结合方式,将w中的6种更新方式表示为wi-QPSO,wi∈w.
2.3 四元数域调和PSO算法四元数因不满足交换律往往导致一些令人意外的结果[15],如由于旋转顺序的差异形成了上述PSO算法的变体,笔者进一步考虑顺序无关的调和(blending)旋转方式.
假设有2个四元数q1和q2,既然直接的相乘存在不可交换的问题,那么基于极限的思想,将q1和q2划分成m份,当m趋近于无穷大的时候,中间相同的部分会越来越多,而两端的不同的部分逐渐趋近于单位四元数而对结果影响越来越小,最终会无限的接近一种稳定的结果,该极限思想的数学表示为
| $ \mathop {{\rm{lim}}}\limits_{m \to \infty } {(q_1^{1/m}q_2^{1/m})^m} = \mathop {{\rm{lim}}}\limits_{m \to \infty } {(q_2^{1/m}q_1^{1/m})^m} $ | (15) |
该式说明了将q1和q2无限分割并交替相乘的结果是可交换的.
由于无法对以上极限的表示直接进行操作,根据文献[16]对极限进行如下转换:
| $ \mathop {{\rm{lim}}}\limits_{m \to \infty } {({{\rm{e}}^{X/m}}{{\rm{e}}^{Y/m}})^m} = {{\rm{e}}^{X + Y}} $ | (16) |
四元数q满足elog q=q.用logq1和logq2替换式(16)的X和Y,得
| $ \mathop {{\rm{lim}}}\limits_{m \to \infty } {(q_1^{1/m}q_2^{1/m})^m} = {{\rm{e}}^{{\rm{log}}{\kern 1pt} {\kern 1pt} {q_1} + {\rm{log}}{\kern 1pt} {\kern 1pt} {q_2}}} $ | (17) |
因此基于顺序无关的调和QPSO的速度变化可表示为
| $ \begin{array}{*{20}{c}} {v_t^{(l)}(n + 1) = }\\ {{\rm{exp}}\left( {\frac{\kappa }{2}{\rm{log}}v_t^{(l)}(n) + \frac{{\kappa {r_1}{\delta _1}}}{2}{\rm{log}}\{ p_t^{(l)}{{[x_t^{(l)}(n)]}^{ - 1}}\} + } \right.}\\ {\left. {\frac{{\kappa {r_2}{\delta _2}}}{2}{\rm{log}}\{ {g^{(l)}}{{[x_t^{(l)}(n)]}^{ - 1}}\} } \right)} \end{array} $ | (18) |
位置变化公式为
| $ x_t^{(l)}(n + 1) = v_t^{(l)}(n + 1)x_t^{(l)}(n){[v_t^{(l)}(n + 1)]^{ - 1}} $ | (19) |
顺序无关的调和QPSO简记为BQPSO.在该算法中,粒子xt(l)本质上是沿惯性方向,以及朝个体最佳pt(l),朝全局最佳g(l)进行无穷多次无穷小旋转所得到的结果.
3 仿真结果及分析由于不同的天线高度和地形地貌会影响路径损耗,进而影响区域的覆盖率,所以选择了理想基站部署和真实基站部署2种场景下的网络进行覆盖率评估.
3.1 实验场景和参数设定为了验证提出方法的有效性,评估了理想7小区和真实大城市的网络场景覆盖性能.在理想7小区场景下,基站均处于边长为250 m的正六边形的小区中心且每个基站部署了3根天线,待测区域共有1 000个采样点且天线的高度为30 m. 图 1所示为西安城区5 km×5 km的区域中地形地貌和基站部署情况,其中红点表示基站,真实场景中的数据包括86个基站、258根天线和3 500个采样点等信息.
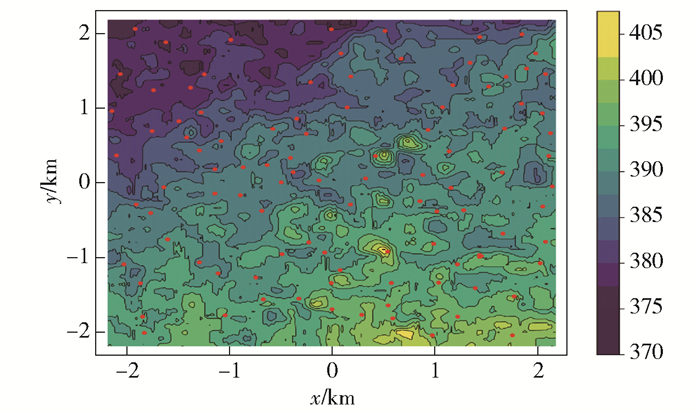
|
图 1 真实场景基站部署 |
在不同场景的仿真中,假设所有天线的发射频率为Ftx=2 600 MHz,发射信号功率ptx=28.2 dBm,接收端的用户增益Gr= 2 dB,阴影衰落余量osf=7.25 dB,加性高斯白噪声σ=-110 dBm.此外SINR的阈值设置为λ=-3 dB.仿真实验中利用了COST231-Hata路径损耗模型计算Tij, s[12].且下倾角上下限分别设置为
| $ U = \frac{\pi }{{12}},L = - \frac{\pi }{{12}} $ |
为了确保实验结果的稳定性,以下每种算法均进行10次实验求平均值,优化性能的对比为平均的性能对比. 2种场景下提出算法与经典PSO、FFA、GA算法的种群大小Na=40;FFA的随机因子α=0.2,吸收因子γ=1.0;GA的交叉概率pc=1.0,变异概率pm=0.3.
3.2 理想场景下的仿真结果理想场景下的不同算法性能对比如图 2所示,随着迭代次数的不断增加,所有算法的覆盖率逐渐上升;提出的wi-OPSO的算法性能表现不同,这验证了四元数表示旋转的不可交换性质;BQPSO算法前期的优化速度相比其他算法稍慢,但后期的覆盖率值逐渐超越其他的算法,且避免陷入局部最优.算法的有效性主要是因为四元数表示旋转确保了天线位置在每次更新的过程中都沿着最短路径进行,且调和算法使得搜索的方向更为合理,提高了PSO算法的搜索效率.此外,对比算法FFA和GA在早期的收敛速度均低于提出算法,这是由于对比算法均独自优化天线的方位角和下倾角,导致搜索空间比较大,收敛速度变慢.
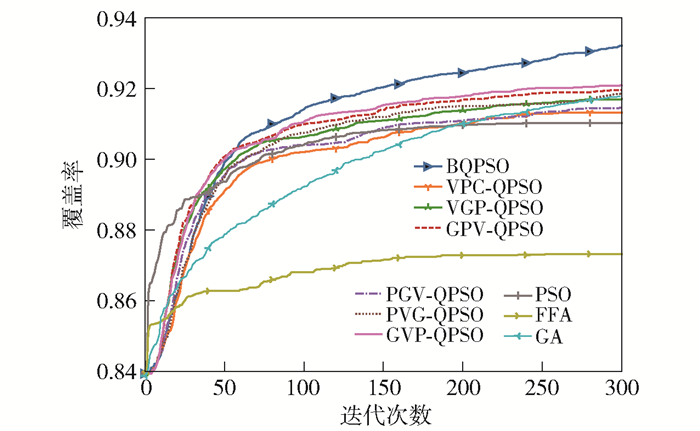
|
图 2 理想场景的算法性能对比 |
图 3为不同的粒子群规模下的算法性能对比图,即Na=20,30,40.由图可知,随着种群规模的不断扩大,经300次迭代后的最终平均网络覆盖率逐渐升高,这是由于更多的粒子参与了寻优过程,更大概率地获得了近似最优解;不同的粒子规模对提出的wi-QPSO算法影响不同,如Na=20时,PVG-QPSO表现最好,Na=30时,VPG-QPSO的最终覆盖率性能最佳,而在Na=40时,GPV-QPSO表现更好,且提出的2种算法最终覆盖率都优于经典PSO,特别是BQPSO算法,最终覆盖性能不仅比经典PSO好而且明显优于提出的wi-QPSO.
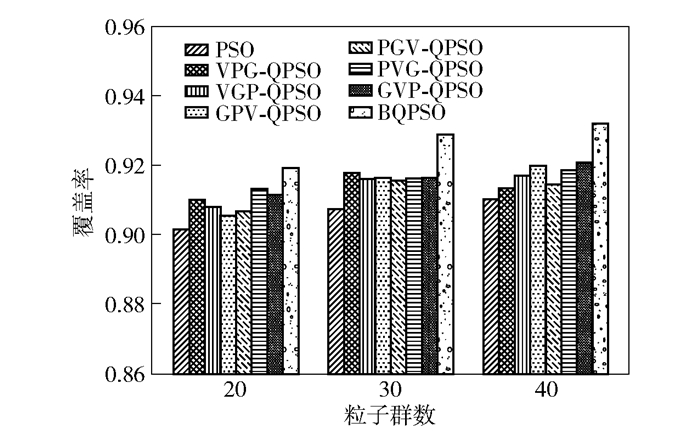
|
图 3 理想场景不同粒子数下的算法性能对比 |
上述提出算法与经典PSO的计算复杂度的分析如下.考虑到待测区域有Nb个基站,每个基站上有n根天线,覆盖率计算在每次迭代中都要计算Np个采样点的覆盖状态,所以经典PSO算法每次迭代的计算复杂度为O(NpNbnNa);而对于提出的QPSO和BQPSO算法在每次迭代过程中将每一根天线的方位角和下倾角变量由式(8)转化为四元数的表示形式,每个粒子额外的计算复杂度为O(Nbn).
综上所述,经典PSO的算法复杂度为O(NpNbnNa).由于每次迭代中评估覆盖率时,提出的BQPSO和QPSO 2种算法需额外消耗O(NbnNa)的时间复杂度,用于实数和四元数之间的转换,但其总体的计算复杂度仍为O(NpNbnNa),通常采样点的数量Np较大,因此所提算法和经典算法在每次迭代上的计算时间近乎相同.
3.3 真实城市场景下的仿真结果真实大城市场景下不同算法的网络覆盖率情况如图 4所示,对比算法的参数设置与理想场景相同.由图可知,各算法的性能与理想场景下的极为相似,但提出算法的有效性相比理想情况更为显著,这是由于不同的地形地貌和天线高度会影响传输信号的路径损耗和接收功率,进而影响整个网络的覆盖情况,使得经典的PSO算法更易陷入局部最优解,而提出的算法中尤其是BQPSO算法具有明显的摆脱局部最优的能力.此外,对比算法FFA和GA的收敛速度亦低于提出算法.
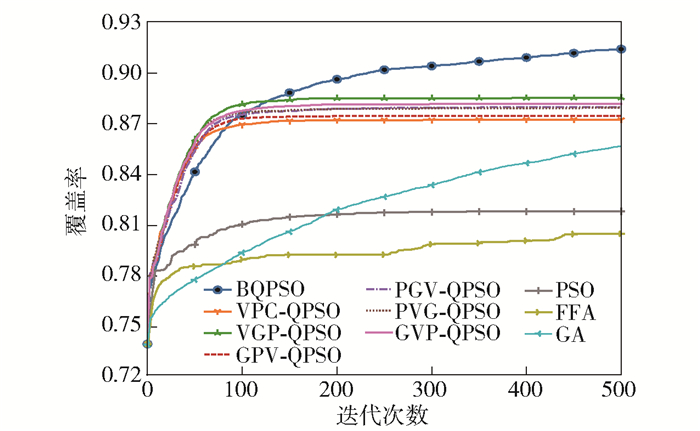
|
图 4 真实城市场景的算法性能对比 |
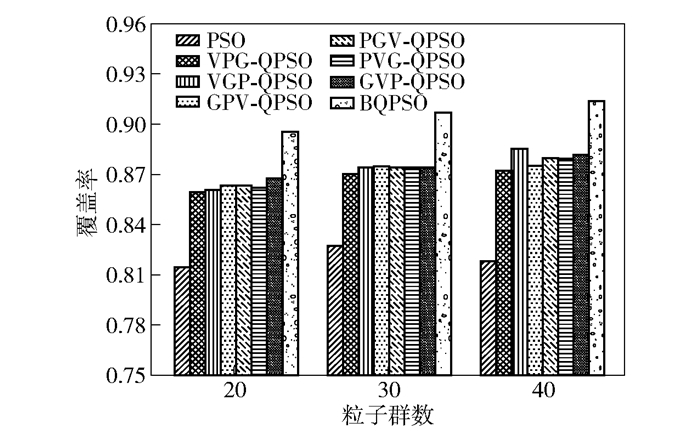
图 5所示为不同粒子规模下网络覆盖率优化情况.由图可知,粒子群的规模与网络覆盖率成正比关系,粒子群规模越大,最终的覆盖越好.当然随着粒子群规模的增加将不可避免的带来额外的计算开销,使得每轮迭代的时间增加.
|
图 5 真实城市场景不同粒子数下的性能对比 |
在移动通信网络的诸多优化任务中,覆盖优化是最基本的任务之一.考虑到已有的关于覆盖优化的研究中通常只考虑方位角或下倾角中的某一个变量,或者将2个变量分开讨论的问题,笔者提出2种四元数域的粒子群优化算法QPSO和BQPSO.前者将天线指向变量从实数域直接拓展到四元数域,用四元数表示天线指向变量,实现了天线方位角和下倾角的联合调整,四元数乘法确保了粒子位置沿最短路径进行更新,提高了算法的收敛速度.后者在此基础之上进一步考虑了四元数乘积表示旋转的不可交换特征,提出了调和四元数粒子群优化算法.实验结果表明,提出的2种算法在最终的覆盖率优化性能上均优于经典PSO和其他对比算法.
| [1] |
Wang Dan, Chen Dong, Song Bin, et al. From IoT to 5G I-IoT:the next generation IoT-based intelligent algorithms and 5G technologies[J]. IEEE Communications Magazine, 2018, 56(10): 114-120. DOI:10.1109/MCOM.2018.1701310 |
| [2] |
易芝玲, 王森, 韩双锋, 等. 从5G到6G的思考:需求、挑战与技术趋势[J]. 北京邮电大学学报, 2020, 43(2): 1-9. Yi Zhiling, Wang Sen, Han Shuangfeng, et al. From 5G to 6G:requirements, challenges and technical trends[J]. Journal of Beijing University of Posts and Telecommunications, 2020, 43(2): 1-9. |
| [3] |
Alsheikh M A, Lin Shaowei, Niyato D, et al. Machine learning in wireless sensor networks:algorithms, strategies, and applications[J]. IEEE Communications Surveys & Tutorials, 2014, 16(4): 1996-2018. |
| [4] |
Park T, Abuzainab N, Saad W, et al. Learning how to communicate in the internet of things:finite resources and heterogeneity[J]. IEEE Access, 2016, 4: 7063-7073. DOI:10.1109/ACCESS.2016.2615643 |
| [5] |
Razavi R, Klein S, Claussen H, et al. A fuzzy reinforcement learning approach for self-optimization of coverage in LTE networks[J]. Bell Labs Technical Journal, 2010, 15(3): 153-175. DOI:10.1002/bltj.20463 |
| [6] |
Zhang Zhongshan, Long Keping, Wang Jianping, et al. On swarm intelligence inspired self-organized networking:its bionic mechanisms, designing principles and optimization approaches[J]. IEEE Communications Surveys & Tutorials, 2014, 16(1): 513-537. |
| [7] |
Qin Yunhui, Huangfu Wei, Zhang Haijun, et al. Accelerated coverage optimization with particle swarm in the quotient space characterizing antenna azimuths of cellular networks[J]. IEEE Access, 2019, 7(13): 86252-86264. |
| [8] |
Zhao Chuanxin, Wu Changzhi, Chai Jian, et al. Decomposition based multi-objective firefly algorithm for RFID network planning with uncertainty[J]. Applied Soft Computing, 2017, 55: 549-564. DOI:10.1016/j.asoc.2017.02.009 |
| [9] |
Wang Yingchen, Geng Xiaoxiao, Zhang Fan, et al. An immune genetic algorithm for multi-echelon inventory cost control of IoT based supply chains[J]. IEEE Access, 2018, 8547-8555. |
| [10] |
Qin Yunhui, Huangfu Wei, Zhang Haijun, et al. Rethinking cellular system coverage optimization: a perspective of pseudometric structure of antenna azimuth variable space[J/OL]. IEEE Systems Journal, 2020[2020-08-19]. https://ieeexplore.ieee.org/document/9103197.
|
| [11] |
Awada A, Wegmann B, Viering I, et al. Optimizing the radio network parameters of the long term evolution system using Taguchi's method[J]. IEEE Transactions on Vehicular Technology, 2011, 60(8): 3825-3839. DOI:10.1109/TVT.2011.2163326 |
| [12] |
Singh Y. Comparison of Okumura, Hata and cost-231 models on the basis of path loss and signal strength[J]. International Journal of Computer Applications, 2012, 59(11): 37-41. DOI:10.5120/9594-4216 |
| [13] |
Valle Y D, Venayagamoorthy G K, Mohagheghi S, et al. Particle swarm optimization:basic concepts, variants and applications in power systems[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(2): 171-195. DOI:10.1109/TEVC.2007.896686 |
| [14] |
Bihan N L, Mars J. Singular value decomposition of quaternion matrices:a new tool for vector-sensor signal processing[J]. Signal Processing, 2004, 84(7): 1177-1199. DOI:10.1016/j.sigpro.2004.04.001 |
| [15] |
Zhang Xirui, Liu Wei, Xu Yougen, et al. Quaternion-valued robust adaptive beamformer for electromagnetic vector-sensor arrays with worst-case constraint[J]. Signal Processing, 2014, 104: 274-283. DOI:10.1016/j.sigpro.2014.04.006 |
| [16] |
Alexamarc. Linear combination of transformations[J]. ACM Transactions on Graphics, 2002, 21(3): 380-387. DOI:10.1145/566654.566592 |



