2. 河南师范大学 智慧商务与物联网技术河南省工程实验室, 新乡 453007;
3. 北京邮电大学 网络与交换技术国家重点实验室, 北京 100876
为提高云平台负载预测的精度,提出了一种基于时序相关性的多负载序列联合预测方法.首先,为获得相似的负载序列,采用长短时记忆网络提取负载序列的时序特征,再利用层次聚类法,获得在时序特征空间相似的负载序列类;其次,对获得的每个负载序列类分别构建多任务学习模型,挖掘和利用负载序列间隐藏的共享领域知识,提高模型泛化能力和预测精度,并实现多个负载序列的联合预测.使用Google数据集的中央处理器负载监控日志进行验证,结果表明,时序特征聚类可有效提取和利用负载序列的全局时序特征,降低原始序列的噪声,获得特征上相似的序列;与常用的负载预测方法比,所提方法对不同变化规律的负载序列都具有更精确的预测效果.
2. Engineering Laboratory of Intelligence Business & Internet of Things, Henan Normal University, Xinxiang 453007, China;
3. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
A novel approach, joint prediction of multi-workload sequences, was proposed based on temporal correlation. Firstly, long short-term memory was used to extract the temporal feature among workload sequences for obtaining the similar workload sequences, while hierarchical clustering algorithm was used to obtain workload sequences clusters. Then, construct multi-task learning model respectively for each obtained sequence clusters, capture and utilize the shared domain knowledge among multiple workload sequences, so as to achieve joint prediction of multiple workload sequences as well as improve generalization ability and prediction accuracy of the model. Results of experiment on dataset of Google cluster trace 2011 demonstrates that the temporal feature clustering can effectively extract and utilize the global temporal feature of workload sequences, reduce the noise of original sequences and get workload sequences clusters with similar characteristics. Proposed method performs better in prediction accuracy than the state-of-the-art methods.
弹性、高效的资源管理是云计算优于其他计算模式的特色.弹性资源管理是指云平台根据资源需求量的变化,动态调整分配资源的数量[1].其中,资源需求量的预测是影响弹性管理算法性能好坏的关键,需求量预测过高会导致额外的资源分配,造成资源浪费;需求量预测不足,用户的部分资源请求得不到满足,降低服务质量.因此,提高云平台资源需求量的预测精度,成为一个亟待解决的问题.
目前云平台负载预测方法已取得一定的进展.传统的时间序列预测模型被引入云负载预测,这类预测模型多为线性模型,具有简单、快速的特点,如自回归移动平均模型[2]、差分自回归移动平均(ARIMA,auto regressive integrated moving average)模型[3]等,但对于云平台中大量存在的非线性变化负载序列,这类方法的预测精度较差.随着机器学习技术的迅速发展,支持向量回归(SVR,support vector regression)[4]、神经网络(NN,neural network)[5-6]等非线性模型被用于云负载序列预测.由于云平台规模的迅速扩展,云平台应用类型、数量急剧增加,云负载序列变化的影响因素更加复杂,序列变化模式更加多样.目前,负载序列变化趋势的影响因素,不仅与负载序列的系统属性、应用类型相关,还与其他负载序列的变化情况有关.例如,Google云平台的Borg系统[7],其资源管理调度系统在资源分配时,会剥夺低优先级的应用程序以释放资源,提供给高优先级的应用程序,故低优先级应用程序的负载变化会受到高优先级应用程序运行资源需求的影响.针对序列模式的多样性,一些集成式预测方法被提出[4, 8-9],并取得了一定预测效果.
然而,已有的预测方法常根据单个序列蕴含的信息建立预测模型,尽管集成方法考虑不同模式的负载序列,但也仅是多个预测模型的简单结合,并未利用负载间的关系.而当负载序列大量增加时,序列间相关性的影响作用会增大,故仅依赖单个负载序列信息构建预测模型,难免无法对影响负载变化趋势的因素进行多视角考虑和利用.另一方面,从构建预测模型的角度看,预测性能的好坏与数据中蕴含的有效信息量具有直接关系,有效信息量越多,预测性能越好.而负载序列之间的相关程度对有效信息的提取和获得将产生重要影响.
基于以上分析可知,若能合理利用相关负载序列之间的关系信息,则可弥补单个负载序列建模信息不足的缺陷,有效提高负载预测模型的准确性.因此,笔者提出一种基于时序相关性的云平台多负载序列联合预测方法,其新颖性在于通过挖掘负载序列在时序特征空间存在的真实相关性,并利用该相关关系实现相关负载序列的联合预测,从而提高云平台负载预测精度.具体地说,该方法首先利用深度学习模型长短时记忆(LSTM,long short-term memory)网络[10-11]提取负载序列的时序特征,将原始空间的序列特征表示变换到序列的时序特征空间,消除原始序列中部分的噪声和冗余信息,实现对序列内在信息的刻画;然后利用层次聚类方法对提取的序列时序特征聚类,从而获得特征空间上相似的负载序列;最后利用多任务学习(MTL,multi-task learning)[12]能捕捉学习任务间相关信息的特点,对获得的相似负载序列类建立MTL模型,挖掘和利用相似负载序列间的共享领域知识,补充单个负载序列信息,从而实现多个负载序列的联合预测.
1 云平台负载序列大规模云平台主要包括事务性和批处理两种类型作业[7],事务性作业指用于面向终端用户的产品,如邮件服务、网页搜索和云平台内部基础设施服务,此类作业的负载变化具有周期性;批处理作业根据云租户的需求产生,负载常呈现出非周期性变化.当作业被数据中心的调度管理模块调度后,资源管理系统开始分配计算或存储节点,并以任务的形式进行执行.每个任务在执行过程中使用的各种资源,如中央处理器(CPU,central processing unit)、随机存储存储器(RAM,random access memory)、输入/输出(I/O,input/output)等,以时间序列的形式被系统记录,形成监控日志.因此,云平台的负载序列是指每个任务的CPU、RAM、I/O等负载序列.不失一般性,下面以CPU负载序列为例进行研究.
设S1, S2, …, Sn表示n个任务的负载序列,第i(i∈{1, 2, …, n})个任务的负载序列定义为一维时间序列Si=(s1, s2, …, sli),sj为第j(j∈{1, 2, …, li},li为该时间序列的长度)时刻消耗的CPU资源,Yk_a表示第k类中第a个任务下一时刻的预测值,nk为第k类中的任务个数(n=n1+n2+…+nk).
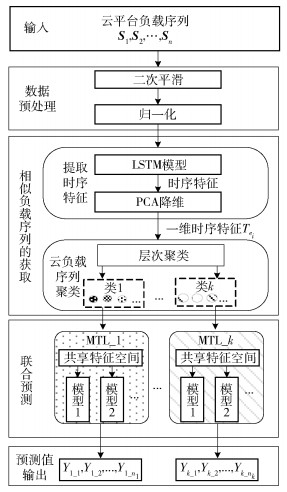
2 基于时序相关性的云平台多负载序列联合预测方法云负载联合预测方法的结构如图 1所示,包括输入、数据预处理、相似负载序列的获取、联合预测和预测值输出5部分,各部分的详细功能描述如下.为方便起见,将该方法简称为JP-TC(joint prediction of multi-workload sequences based on temporal correlation).
|
图 1 JP-TC的结构 注:图中不同图案的○代表类中不同的负载序列. |
实际负载原始序列中存在噪声,故首先对每个任务的原始负载序列进行二次平滑,过滤部分噪声;为消除序列在幅值上的差异,接着对平滑后的数据进行归一化(见式(1)),Si*为归一化后的负载序列,Si*=(s1*, s2*, …, s*li),Smax和Smin分别为该序列中的最大值和最小值.
| $ s_i^* = \frac{{{s_i} - {S_{{\rm{min}}}}}}{{{S_{{\rm{max}}}} - {S_{{\rm{min}}}}}} $ | (1) |
1) 时序特征的提取
时序特征提取指通过对时间序列进行挖掘,去除噪声和冗余信息,从而获得该时间序列的全局时序特征和隐藏的本质信息.近年来,随着深度学习技术的快速发展,出现了时序特征提取模型. LSTM由于能够实现对当前时刻神经元的信息进行记忆,并可以学习时序数据的长期依赖关系,将保留的历史信息用于以后时刻的计算中,因此采用LSTM提取每个任务负载序列的时序特征.
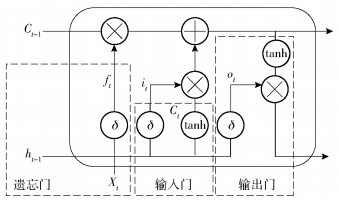
LSTM是一种具有长期记忆功能的循环NN,每个隐藏层的神经元中加入记忆单元,通过“门”结构来控制信息的取舍.其主要包括遗忘门、输入门和输出门,单元结构如图 2所示. ht-1和Ct-1分别代表LSTM记忆单元前一时刻的输出和状态信息,δ为sigmoid函数.遗忘门ft控制前一时刻记忆单元状态信息的保留度,有
|
图 2 LSTM记忆单元结构 |
| $ {f_t} = \delta ({\mathit{\boldsymbol{W}}_f}[{h_{t - 1}},{\mathit{\boldsymbol{X}}_t}] + {b_f}) $ | (2) |
输入门it实现当前时刻状态信息的去除或保留,见式(3),即时状态信息见式(4).
| $ {{i_t} = \delta ({\mathit{\boldsymbol{W}}_i}[{h_{t - 1}},{\mathit{\boldsymbol{X}}_t}] + {b_i})} $ | (3) |
| $ {{C_t} = {\rm{tanh}}({W_C}[{h_{t - 1}},{\mathit{\boldsymbol{X}}_t}] + {b_C})} $ | (4) |
输出门ot控制信息的输出,见式(5)和式(6).
| $ {{o_t} = \delta ({\mathit{\boldsymbol{W}}_o}[{h_{t - 1}},{\mathit{\boldsymbol{X}}_t}] + {b_o})} $ | (5) |
| $ {{h_t} = {o_t}{\rm{tanh}}({C_t})} $ | (6) |
记忆单元当前时刻状态信息Ct见式(7).
| $ {C_t} = {f_t}{C_{t - 1}} + {i_t}{C_t} $ | (7) |
式(2)~式(5)中的W和b分别代表对应门中的权重和偏置.
为获得该负载序列更具有代表性的时序信息,实现特征属性之间关联关系的有效利用,采用主成分分析法(PCA,principal component analysis)对时序特征进行降维,得每个任务一维时序特征Tci.
2) 负载序列的聚类
对每个负载序列的一维时序特征进行聚类,获取在时序特征空间具有较高相似度的任务.因层次聚类算法具有稳定和通用等优点,故采用其作为聚类方法[13].负载序列之间相似度的计算对聚类结果产生重要的影响,考虑到任务运行的时长不同,即提取一维时序特征的长度不同,故采用动态时间弯曲距离衡量2个任务在时序特征空间中的相似性.同时,选择轮廓系数来确定聚类个数.
2.3 联合预测为充分挖掘和利用负载序列间的关联信息,对聚类获得的每一类分别构建MTL模型,各类中每个任务的原始负载序列作为该类多任务预测模型中的一个学习任务.采用基于迹范数正则化的MTL模型,在最小化经验风险的基础上,添加核范数正则项,约束不同学习任务的模型共享到一个低维子空间,有
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{W}} \sum\limits_{i = 1}^l {\left\| {\mathit{\boldsymbol{w}}_i^{\rm{T}}{\mathit{\boldsymbol{X}}_i} - \mathit{\boldsymbol{Y}}} \right\|_{\rm{F}}^2} + \rho {\left\| \mathit{\boldsymbol{W}} \right\|_ * } $ | (8) |
其中:l为学习任务的个数,W=[w1, w2, …, wl]为权重矩阵,wi为第i个学习任务的权重向量,Xi和Yi分别为第i个学习任务的输入和输出,超参数ρ控制W的秩‖W‖*.由于权重矩阵蕴含了样本数据之间重要的结构化信息,对于建立模型十分重要,而矩阵低秩表示该矩阵中的向量具有高度的相关性,故对l个学习任务同时采用梯度下降法求解权重,使用核范数对所得的权重矩阵进行约束,直到其取得低秩,表明此时获得了合理的模型空间,在该模型空间中,领域特定的通用知识被多个学习任务共享,提升了每个学习任务的学习性能,从而实现同一个类内所有任务的联合学习以及多个任务的同时预测.
2.4 预测输出采用MTL模型,实现多个任务负载序列的同时输出,即对每一个聚类结果分别构造MTL模型作为其预测模型,从而得到每个任务在未来时刻所需的负载量Yk_nk.
3 实验结果与分析 3.1 实验数据的选择采用Google trace dataset进行验证,验证所提方法能有效消除原始序列中的噪声和冗余信息,捕捉时序特征性.该数据集是Google数据中心公开的2011年5月期间的监控日志,记录了多个计算节点29天的运行情况,包括约672 074个作业,2 600万个任务[14].实验数据从数据集前3天的日志数据中分别随机选择两类负载:周期性变化作业和非周期性变化作业.限于篇幅,不失一般性,分别从周期性作业和非周期性作业中均任意选择一个作业(周期性作业ID:17109330,非周期性作业ID:6280685099),2个作业具有的任务数和运行长度如表 1所示.由于监控中心是每5 min作为一个采样间隔,故将采样的点数作为该任务的运行长度.
|
|
表 1 实验作业的基本属性 |
实验分为2组:基于时序特征聚类的相似负载序列获取和预测结果的比较及分析,包括不同变化规律的负载序列预测效果分析、与当前常用预测方法的比较和分析.
基准预测方法有ARIMA[3]、SVR[4]、传统NN[5]和LSTM[10].其中,ARIMA是典型的时间序列预测模型,属于线性预测模型;SVR、传统NN和LSTM都是机器学习方法,属于非线性模型,对于传统的NN模型,选择其中一种前馈NN极限学习机(ELM,extreme learning machine)进行对比.
3.3 评价指标采用4种不同性能度量方法评价预测结果,分别是均方根误差(RMSE,root mean square error)(记为R1)、平均绝对误差(MAE,mean absolute error)(记为R2)、平均相对误差(MRE,mean relative error)(记为R3)、对称平均绝对百分比误差(SMAPE,symmetric mean absolute percentage error)(记为R4),见式(9)~式(12).
| $ {{R_1} = \sqrt {\frac{1}{L}\sum\limits_{i = 1}^L {{{({y_{{\rm{ 预测值}}(i)}} - {y_{{\rm{ 实际值 }}(i)}})}^2}} } } $ | (9) |
| $ {{R_2} = \frac{1}{L}\sum\limits_{i = 1}^L | ({y_{{\rm{ 预测值 }}(i)}} - {y_{{\rm{ 实际值 }}(i)}})|} $ | (10) |
| $ {R_3} = \frac{1}{L}\mathop \sum \limits_{i = 1}^L \left[ {\frac{{{y_{{\rm{ 预测值 }}(i)}} - {y_{{\rm{ 实际值 }}(i)}}}}{{{y_{{\rm{ 实际值 }}(i)}}}}} \right] $ | (11) |
| $ {R_4} = \frac{1}{L}\sum\limits_{i = 1}^L {\left| {\frac{{{y_{{\rm{ 预测值 }}(i)}} - {y_{{\rm{ 实际值 }}(i)}}}}{{{y_{{\rm{ 预测值 }}(i)}} + {y_{{\rm{ 实际值 }}(i)}}}}} \right|} $ | (12) |
其中i{1, 2, …, L},表示第i个样本点. RMSE表示模型预测值对实际值的平均偏离程度,MAE反映预测值误差的实际情况,MRE衡量预测的可信程度,SMAPE揭示预测值在真实值上的波动范围.
3.4 实验结果和分析 3.4.1 基于时序特征聚类的相似负载序列获取因时序特征的提取层面对负载序列进行分析,可获得本质上更具有相似性的负载序列.在实验中,采用平均轮廓系数确定最佳聚类簇数.平均轮廓系数越大,说明聚类结果越好.其中,周期性作业的聚类簇数设为7,非周期性作业的聚类簇数设为4.
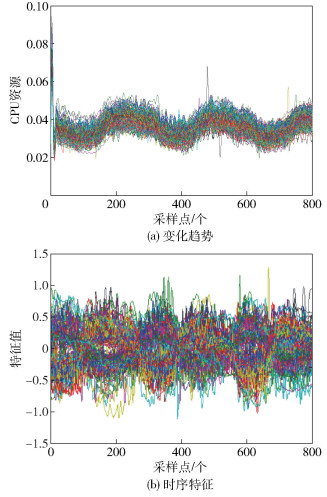
为进一步直观展示基于时序特征聚类后可得到具有相似性的负载序列,以周期性作业的结果为例,首先对该作业中所有任务负载序列的变化趋势和时序特征进行可视化,如图 3所示;然后分别给出基于时序特征聚类后和基于原始序列聚类后负载序列的变化趋势图和时序特征图,如图 4所示.对聚类后的结果均以第3类进行展示,这2种聚类结果的第3类中的任务不完全相同.
|
图 3 原始负载序列变化趋势和时序特征 |

|
图 4 2种不同聚类方式下第3类中任务负载序列聚类结果的比较 |
由图 3(a)可见,同一个作业中的任务,其负载序列具有相似的变化模式,图 3(b)是每个任务负载序列的时序特征.明显可以看出,同一个作业中的任务,虽然在原始空间上具有相似的变化模式,但映射到时序特征空间上仍具有一定的差别. 图 4(a)和(b)分别是基于时序特征聚类后,第3类中任务的负载序列变化趋势和时序特征;图 4(c)和(d)则分别是基于原始序列聚类后,第3类中任务的负载序列变化趋势和时序特征.
由图 4(a)和(b)可以看出,该类中的任务在原始变化趋势上是相似的,虽然某些任务负载序列的时序特征存在离群现象,但大多数任务在时序特征空间中仍具有较高相似度.由图 4(c)和(d)可以发现,直接对任务的原始负载序列进行聚类,虽然可以得到形态上相似的任务,但由于时序数据存在噪声,故往往不能捕捉其真实的数据特征,使得聚类后得到任务的时序特征具有较大的差别.相反地,在时序特征空间中进行聚类,提取并利用负载序列的全局时序特征,从而降低了噪声对聚类结果的影响,既保证了任务的负载序列在变化形态上的相似,同时也可获得了其在特征空间的相似.
3.4.2 预测结果及分析分别从周期性作业和非周期性作业中任选2个任务.预测输入前,对每一个任务的负载序列进行相空间重构[15],嵌入维和时延均为9和1.对于SVR,采用5折交叉验证法寻找最优参数;ELM隐藏层的神经元个数设置为20.采用单层LSTM模型进行时序特征提取,其中周期性作业的隐藏层神经元个数为100,非周期性作业的隐藏层神经元个数为25,学习率均为0.001,迭代次数均为500次.
1) 周期性作业的负载预测
该类中2个任选的任务分别为第43个和第61个,记为任务1和任务2. 表 2和图 5分别是任务1和任务2的预测结果.
|
|
表 2 任务1在不同评价指标下的预测结果比较 |

|
图 5 多种预测方法对任务2的预测结果 |
由表 2可得,在不同评价指标中,所提方法均具有最小的预测误差,相比于SVR和NN,4种指标的误差分别降低14.01、13.10、12.37、12.24、74.2、68.2、67.68、67.67%.从图 5可以看出,所提方法的预测误差仍最小.观察发现,对于周期性作业的任务,NN模型都取得最差的预测效果.这是因为ELM模型随机生成权重信息,波动性较大,故预测结果不稳定.
2) 非周期性作业的负载预测
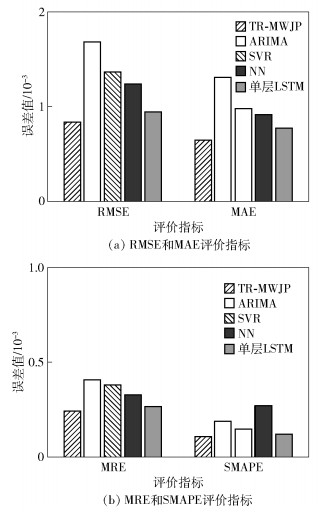
云平台存在大量非周期性作业,与规律性较强的周期性作业相比更难预测,故任选2个非周期性变化的任务,即第43个和第45个,记为任务3和任务4. 表 3和图 6所示分别为任务3和任务4的预测结果.
|
|
表 3 任务3在不同评价指标下的预测结果比较 |
|
图 6 多处预测方法对任务4的预测结果 |
表 3展示了任务3在不同预测方法和不同评价指标的预测结果,可以看出,所提方法的预测误差均明显小于其他方法,相比于单层LSTM和ARIMA,4种指标的误差分别降低15.92、21.22、9.04、17.02%和64.43、63.34、52.86、54.22%.观察图 6可发现,所提方法与其他4种预测方法相比,预测误差都是最小.结合表 3和图 6得,对非周期性作业的2个任务,ARIMA模型的预测误差均最高.这是因为云平台任务负载序列中普遍存在非线性关系,而ARIMA模型的线性属性难以捕捉到负载序列的变化规律,故导致预测性能较差.
综合2种类型负载序列的预测结果可见,所提方法均取得了最好的预测性能.由于ARIMA/SVR/NN/单层LSTM都仅考虑单个任务的负载序列,未能对时序数据中存在的时序特征、任务之间的关联信息进行有效挖掘和利用,从而使得预测误差较大.所提方法不仅考虑了单个任务的负载序列内的时序信息,也有效利用了任务与任务之间的关联信息,从而表现出较好的预测性能.
4 结束语准确地进行负载预测对云平台的资源管理具有重要意义.为提高负载预测模型的准确度和泛化性能,提出一种基于时序相关性的云平台多负载序列联合预测方法.其通过深层次提取负载序列的时序信息,并根据提取的时序特征将相似负载序列进行聚类,在获得序列聚类基础上,引入MTL模型捕捉序列间隐藏的关联性,从而使每个任务预测时不仅使用自身特性,同时也利用相关负载序列间的关联信息,提高预测模型的准确度和泛化能力.
因大规模云平台负载序列变化趋势的影响因素复杂,故下一步将继续深入研究复杂的影响因素和变化趋势之间的相关性,以获得更佳的预测性能.
| [1] |
Al-Dhuraibi Y, Paraiso F, Djarallah N, et al. Elasticity in cloud computing:state of the art and research challenges[J]. IEEE Transactions on Services Computing, 2017, 11(2): 430-447. |
| [2] |
Yang Jingqi, Liu Chuanchang, Shang Yanlei, et al. A cost-aware auto-scaling approach using the workload prediction in service clouds[J]. Information Systems Frontiers, 2014, 16(1): 7-18. |
| [3] |
Calheiros R N, Masoumi E, Ranjan R, et al. Workload prediction using ARIMA model and its impact on cloud applications' QoS[J]. IEEE Transactions on Cloud Computing, 2014, 3(4): 449-458. |
| [4] |
Liu Chunhong, Liu Chuanchang, Shang Yanlei, et al. An adaptive prediction approach based on workload pattern discrimination in the cloud[J]. Journal of Network and Computer Applications, 2017, 80: 35-44. DOI:10.1016/j.jnca.2016.12.017 |
| [5] |
Islam S, Keung J, Lee K, et al. Empirical prediction models for adaptive resource provisioning in the cloud[J]. Future Generation Computer Systems, 2012, 28(1): 155-162. DOI:10.1016/j.future.2011.05.027 |
| [6] |
Hoang M N, Gaurav K, Daeyoung K. Host load prediction in cloud computing using long short-term memory encoder-decoder[J]. The Journal of Supercomputing, 2019, 75(11): 7592-7605. DOI:10.1007/s11227-019-02967-7 |
| [7] |
Verma A, Pedrosa L, Korupolu M, et al. Large-scale cluster management at Google with Borg[C]//ECCS 2015: Proceedings of the Tenth European Conference on Computer Systems. New York: ACM, 2015: 18-35.
|
| [8] |
Jiang Yexi, Perng Changshing, Li Tao, et al. Cloud analytics for capacity planning and instant vm provisioning[J]. IEEE Transactions on Network and Service Management, 2013, 10(3): 312-325. DOI:10.1109/TNSM.2013.051913.120278 |
| [9] |
Parminder S, Pooja G, Kiran J. Tasm:technocrat arima and SVR model for workload prediction of web applications in cloud[J]. Cluster Computing, 2019, 22(2): 619-633. DOI:10.1007/s10586-018-2868-6 |
| [10] |
Kumar J, Goomer R, Singh A K. Long short term memory recurrent neural network (LSTM-RNN) based workload forecasting model for cloud datacenters[J]. Procedia Computer Science, 2018, 125: 676-682. DOI:10.1016/j.procs.2017.12.087 |
| [11] |
Janardhanan D, Barrett E. CPU workload forecasting of machines in data centers using LSTM recurrent neural networks and ARIMA models[C]//ICITST 2017: the 12th International Conference for Internet Technology and Secured Transactions. Cambridge: IEEE, 2017: 55-60.
|
| [12] |
Zhou Jiayu, Chen Jianhui, Ye Jieping. Malsar: multi-task learning via structural regularization[EB/OL]. 2012(2012-12-18)[2019-11-10]. http://www.MALSAR.org.
|
| [13] |
徐前方, 王嘉春, 肖波. 融合时空上下文信息的兴趣点推荐[J]. 北京邮电大学学报, 2018, 41(1): 37-42, 50. Xu Qianfang, Wang Jiachun, Xiao Bo. Point-of-interest recommendation with spatio-temporal context awareness[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(1): 37-42, 50. |
| [14] |
Reiss C, Wilkes J, Hellerstein J L. Google cluster-usage traces: format+ schema[EB/OL]. 2014(2014-11-17)[2019-11-10]. https://github.com/google/cluster-data.
|
| [15] |
Han Li, Romero C E, Yao Zheng. Wind power forecasting based on principle component phase space reconstruction[J]. Renewable Energy, 2015, 81: 737-744. DOI:10.1016/j.renene.2015.03.037 |



