2. 天津市成像与感知微电子技术重点实验室, 天津 300072
时间数字转换电路(TDC)的分辨率、线性度、温度适应范围等参数指标直接影响着激光雷达系统的测距精度和成像清晰度.基于Xilinx Artix-7系列28 nm工艺的现场可编程门阵列(FPGA)芯片,设计了一种以进位链为延时单元的高分辨率双链三路TDC.该TDC可打破延时单元的分辨率限制,细分进位链中的宽码,具有低成本、高分辨率的优势.设计了流水线编码电路,以提高逻辑单元的使用效率,采用码密度方案逐一确定bin宽的精确值和等效分辨率.调用FPGA中赛灵思的特殊模数转换器(XADC)模块测量芯片温度,进而转换为温度校准系数,修正测量值.常温(27 ℃)下的等效bin宽为5.63 ps,方均根测量数值为11.7 ps,电路可在5~85 ℃温度范围内完成温度补偿.相比于六链延时线TDC,双链三路TDC具有相近的指标参数,并使FPGA逻辑资源使用降低约43.1%,芯片功耗降低约36.8%.
2. Tianjin Key Laboratory of Imaging and Sensing Microelectronic Technology, Tianjin 300072, China
The ranging accuracy and image sharpness of radar system are directly related to parameters of time-to-digital converter(TDC), including measurement resolution, linearity, temperature adaptability and so on. A double-chain three-route TDC with high-resolution is designed based on Xilinx 28 nm Artix-7 field programmable gate array(FPGA), which could break the resolution limitation of the single delay tap and effectively subdivide the wide tap. The structure offers significant advantages of low cost and high resolution. The pipeline encoders are designed to economize logic cells. The code density scheme is used to determine the exact value of the bin width one by one and the equivalent resolution. The chip temperature is determined according to the xilinx analog to digital converter module in the FPGA and the temperature calibration coefficient could be obtained to correct the measurement value. Parameter indexes of the TDCs included 5.63 ps equivalent bin width and 11.7 ps root mean square resolution under normal temperature. The compensation is finished in the circuit in the range from 5 ℃ to 85 ℃. Compared with the six-chain delay line TDC, the double-chain three-route TDC has the similar index, which reduces the utilization of logic resources of the FPGA by up to 43.1% and cuts power consumption by up to 36.8% respectively.
激光雷达系统通过发射激光束来探测目标物体的轮廓、位置、速度等信息.激光测距系统的主流方法为飞行时间测量方案[1],测距信息来源于入射信号与回波信号的时间间隔值.时间测量精度直接决定测距系统的参数性能.时间数字转换电路(TDC, time-to-digital converter)作为激光雷达系统的重要模块,具有高分辨率和线性度好的优势.
计数型TDC受限于时钟频率,实现ps级分辨率指标需要太赫兹频率的时钟信号,这在实际电路中很难实现.研究人员采用多种方法提升TDC分辨率,包括模拟时间放大法、游标法、抽头延迟线法、Wave Union等方案.
TDC采用粗细结合测量方案[2]可兼顾宽量程和高分辨率,如图 1所示,基于二进制计数法完成粗时间测量,在宽量程时间测量中,可选用格雷码计数来规避亚稳态现象.时间测量值T为
| $ T = n{T_{{\rm{clk}}}} + \Delta {T_1} - \Delta {T_2} $ | (1) |
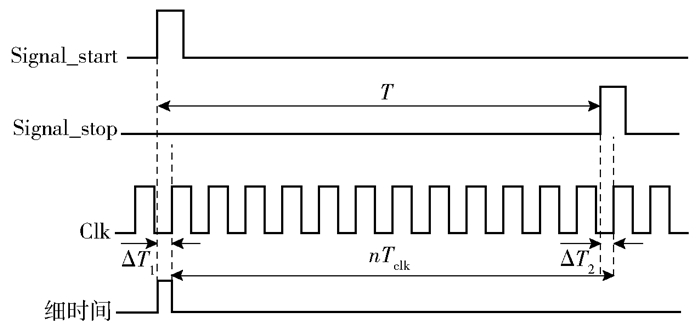
|
图 1 粗细结合TDC时序图 |
基于现场可编程门阵列(FPGA, field programmable gate array)开发TDC具有研发周期短、设计成本低、设计灵活性高等优势.国内外学者针对FPGA-TDC的分辨率、方均根(RMS, root mean square)精度、微分非线性、积分非线性、死区时间、功耗等众多参数进行优化,提出多种设计方案. 2010年,Bayer等[3]基于Wave Union A方案,在Virtex-4 FPGA中完成了48通道分辨率为10 ps的TDC. 2014年,Pan等[4]在30 ps分辨率Cyclone FPGA-TDC中引入了温度补偿方案. 2015年,Shen等[5]基于多链测量平均法有效提升了TDC的分辨率,并通过修改测量链数目实现了分辨率的调整. 2017年,Chen等[6]结合柱状图分布调整TDL-TDC,有效提升了测量数据线性度.
笔者针对激光雷达系统中的测时电路,基于28 nm工艺Artix-7系列FPGA设计TDC,具有高分辨率、RMS精度高、可温度补偿、成本低廉等优势.
1 TDC设计方案分析 1.1 传统抽头延迟线结构TDC抽头延迟线[7]TDC为FPGA-TDC的主流设计方案,具有分辨率高、线性度好的优势.如图 2所示,在细测量模块,采用加法器级联的方法构造进位链,加法器作为基本延时单元,延时时间决定了TDC的分辨率,各延时单元依次与D触发器连接,记录细时间信号在延时链中传播的位置.采用温度计编码,如在8位温度计码输出中,D触发器的初始数据为“11111111”,细时间信号传入延时链时,温度计码输入依次发生1~0的切换,细时间测量结束后,D触发器记录最终测量结果.例如,温度计码显示“11111000”,表明细时间的测量值为3个延时单元的延时总和.根据电路模型分析,各延时单元延时Dtap由4部分构成[8],即
| $ {D_{{\rm{tap}}}} = {D_1} + {D_T} + {D_S} + {D_C} $ | (2) |
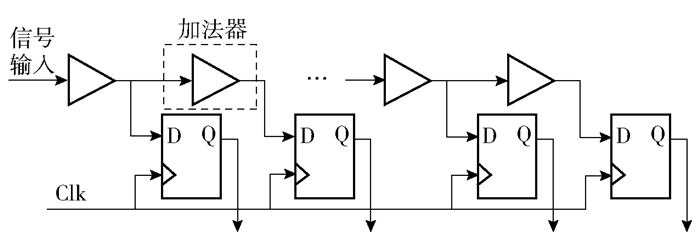
|
图 2 抽头延迟线TDC工作原理 |
其中:DI为无输出负载门延时,即本征延时;DT为输出负载引入的延时;DS为输入信号斜率造成的延时;DC为门输出端走线延时.传统抽头延迟线TDC(TDL-TDC)分辨率受限于延时单元,延时单元来源于FPGA中各Slice配置的加法进位资源.由芯片版图可知,各Slice之间存在较大的走线延时,这降低了TDC测量线性度,DNL/INL等指标参数也会恶化.
1.2 双链三路TDC结构分析为实现TDC分辨率、RMS精度、DNL/INL等指标参数的优化,需对单链抽头延迟线TDC进行改进.多链延迟线TDC采用多链同步测量方案,可有效提升分辨率[5].基于Artix-7系列FPGA多链延迟线TDC的各项参数取决于测量链数.伴随测量链数目的上升,分辨率可有效提升,但DNL/INL指标会变差,FPGA资源消耗增多,功耗也会上升.实验中,六链延迟线TDC可充分适应激光雷达探测器的各项要求,具有高分辨率、高RMS精度、DNL/INL参数良好等优势.如图 3所示[5],六链延迟线TDC需6条进位链并行测量,消耗逻辑资源较多,芯片功耗亦会随之上升.
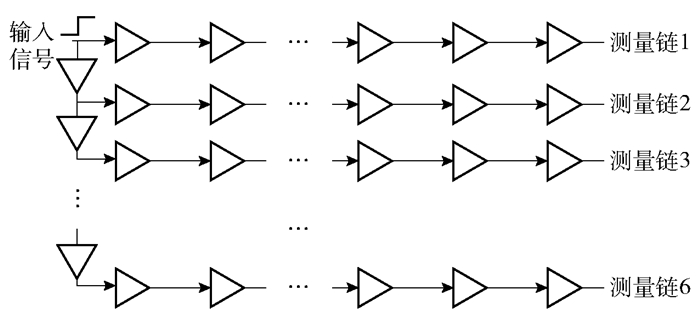
|
图 3 六链并行TDC测量结构 |
为了进一步优化六链延迟线TDC的指标,既保有其优良的分辨率、RMS精度等参数,同时也减少FPGA逻辑资源消耗,降低芯片功耗,设计双链三路TDC测量结构.如图 4(a)所示,主体结构分为路径选择区和测量区.路径选择区包括多路选择器MUX和延时模块delay_1和delay_2.细时间测量中,多路选择器控制输入信号的流通路径,包括路径A、路径B和路径C.测量区包括2条测量延时链,测量链由多位加法器级联构成.
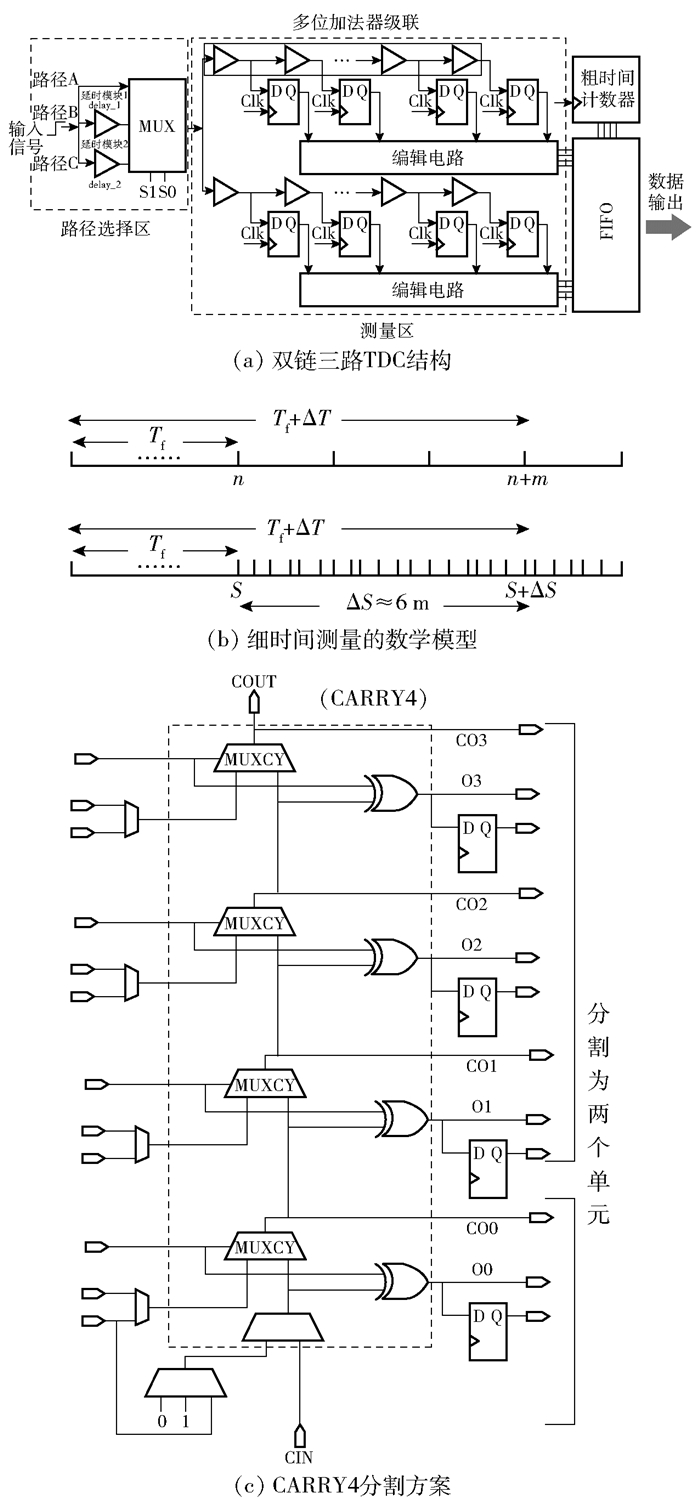
|
图 4 双链三路TDC设计方案 |
方案中,激光雷达采集三路完全相同的时间间隔信号.在细时间测量模块,由双链三路TDC完成高精度测量.细时间分别位于Signal_start上升沿信号附近与Signal_stop上升沿信号附近.这里具体分析三路时间在Signal_start上升沿附近的3个细时间Tf.
3个细时间Tf完全相同,图 4(a)所示结构将细时间Tf分为2部分,包括路径选择区延时和测量区延时.路径选择区中,3条路径的延时时间不同,分别定义为tα、tβ、tθ. 图 4(a)中delay_1和delay_2为2个不同延时模块,tα为多路选择器的延时,tβ为多路选择器与delay_1的延时总和,tθ为多路选择器与delay_2的延时总和.在测量区中,2条测量链为加法器级联所构成的进位链,可将2条链延时单元的等效延时标记为τ1和τ2.延时链存在测量非线性,τ1和τ2受FPGA制造工艺及底层布局布线的影响,但总体说来,τ1≈τ2.在第1条测量链中,细时间Tf为
| $ \begin{array}{*{20}{c}} {{T_{\rm{f}}} = {t_\alpha } + j{\tau _1} + \Delta {\tau _j}\left( {0 < \Delta {\tau _j} < {\tau _1}} \right) = }\\ {{t_\beta } = k{\tau _1} + \Delta {\tau _k}\left( {0 < \Delta {\tau _k} < {\tau _1}} \right) = }\\ {{t_\theta } + l{\tau _1} + \Delta {\tau _l}\left( {0 < \Delta {\tau _l} < {\tau _1}} \right)} \end{array} $ | (3) |
第1条测量链中的Δτj、Δτk和Δτl为3条路径测量误差.参数tα、tβ和tθ分别对应3条测量路径,基于3条路径测量3个相同细时间Tf.进位链的每个延时单元不可避免地存在差异性,每次测量对应的最后一个延时单元不同,细时间结束点落入小延时单元的概率增大.同理,第2条测量链延时单元延时时间为τ2,细时间Tf为
| $ \begin{array}{c} {T_{\rm{f}}} = {t_\alpha } + p{\tau _2} + \Delta {\tau _p}\left( {0 < \Delta {\tau _p} < {\tau _2}} \right) = \\ {t_\beta } = q{\tau _2} + \Delta {\tau _q}\left( {0 < \Delta {\tau _q} < {\tau _2}} \right) = \\ {t_\theta } + r{\tau _2} + \Delta {\tau _r}\left( {0 < \Delta {\tau _r} < {\tau _2}} \right) \end{array} $ | (4) |
第2条测量链中的Δτp、Δτq和Δτr为3条路径测量误差.传统抽头延迟线结构TDC中,细时间Tf=nτ,分辨率τ=Tf/n.双链三路TDC可有效实现电路性能的提升.由式(3)和式(4)可知,第1条测量链3次测量结果为j、k、l,第2条测量链3次测量结果为p、q、r.采用6个数值总和S(S=j+k+l+p+q+r)表征细时间Tf,细时间的微小变化即可导致S的改变.
图 4(b)为双链三路TDC完成细时间测量的数学模型.图上半部分代表了单链抽头延迟线TDC的测量过程,当细时间数值从Tf变化至Tf+ΔT时,测量结果从n变化至n+m,分辨率为ΔT/m.图下半部分代表了双链三路TDC的测量过程,当细时间数值从Tf变化至Tf+ΔT时,6个值j、k、l、p、q和r分别转变为j+m1、k+m2、l+m3、p+m4、q+m5和r+m6,测量结果从S转变为S+ΔS (ΔS=m1+m2+m3+m4+m5+m6),且知m≈m1≈m2≈m3≈m4≈m5≈m6.即有ΔS≈6m.该方案近似将ΔT分割为ΔS格,分辨率近似为ΔT/6m.这有效提升了测量分辨率.实际电路中,细时间每一格的长度存在差异,即需综合考虑TDC的非线性问题,还需依据DNL/INL特性进行数据校准.
双链三路TDC结构与六链TDC具有相近测量分辨率.六链TDC并行测量同样可采集6个数据值,相比之下,双链三路TDC消耗更低的FPGA逻辑资源,进而具有低功耗的优点,有利于扩展为多通道TDC.
TDC中的加法器来源于FPGA的CARRY4逻辑单元,CARRY4集成四位加法器,且CARRY4逻辑单元之间存在不可忽略的走线延时.如图 4(c)所示,为了降低TDC测量数据非线性,CARRY4逻辑单元被分割为2个延时单元[9],该分割方案可有效改善DNL/INL指标.
TDC调用pll倍频生成400 MHz时钟信号,平均每个延时单元为33 ps,这意味着需要76个延时单元.电路设计每条测量链包含40个CARRY4逻辑单元(80个延时单元),双链三路TDC共包括160个延时单元,三路测量即可获取6组80位温度计码.粗测量使用16位计算器,测量范围为0~163.83 μs.
1.3 流水线编码电路如图 5所示,采用流水线编码电路[10]完成6组80位温度计码编码.相比于直接编码法和折半查找编码方案,流水线编码可有效节约逻辑资源.第1阶段,调用FPGA中6输入查找表,完成6-3编码二进制输出.第2阶段,将所有3 bit码字两两相加,输出4 bit码字.基于该方法依次累加输出值,在最后阶段可得出9 bit编码结果.
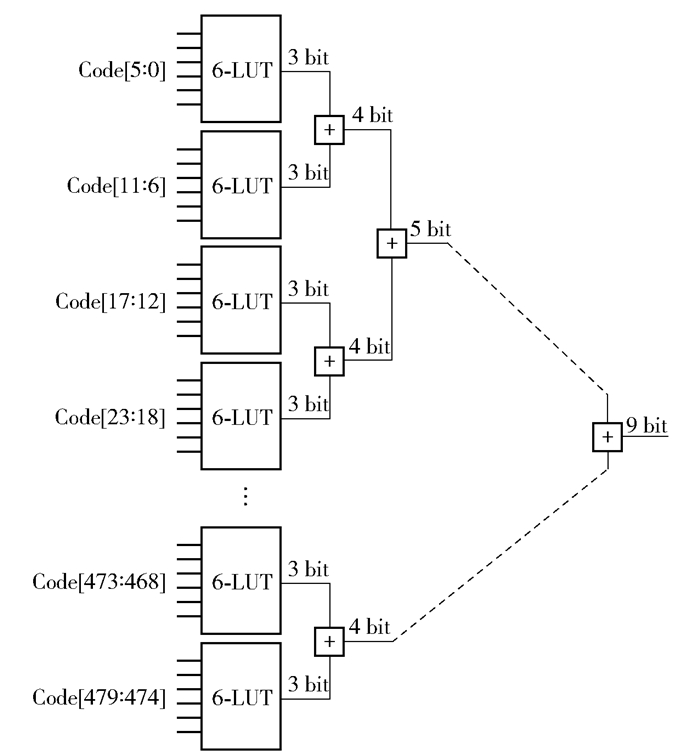
|
图 5 流水线编码电路结构 |
TDC每个bin的宽度存在差异,码密度统计校准方案可精确确定所有bin的宽度值.大量细时间信号(信号个数为N)输入TDC测量电路,Tc为时钟周期2.5 ns,细时间数值在(0, Tc)中随机均匀分布,bin宽越大,细时间stop点落入该bin的概率越大,每个bin连接计数器,统计stop点落入该bin的次数nj(第j个bin),构造离散柱状图,进而可计算bin宽的精确值,如图 6所示,第j个bin宽度的估计值wj为
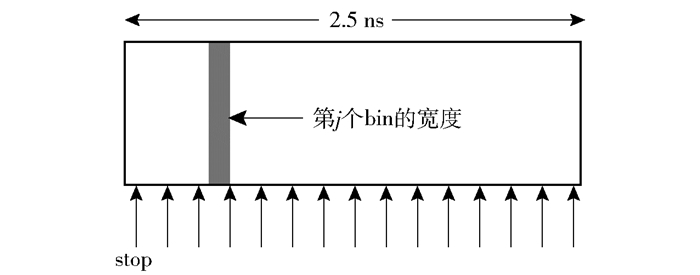
|
图 6 TDC模型下第j个bin宽数值 |
| $ {w_j} = \frac{{{n_j}}}{N}{T_{\rm{c}}} $ | (5) |
N值越大,量化误差越小.时间测量值tj为
| $ {t_j} = \sum\limits_{k = 0}^j {{w_k}} $ | (6) |
测量误差为1个bin,时间准确值td的范围为tj-1<td<tj-1+wj,测量标准差为
| $ {\sigma ^2} = \frac{1}{{{w_j}}}\int_{{t_{j - 1}}}^{{t_j}} {{{\left( {t - {t_{\rm{d}}}} \right)}^2}{\rm{d}}t = \frac{{{{\left( {{t_j} - {t_{\rm{d}}}} \right)}^3} - {{\left( {{t_{j - 1}} - {t_{\rm{d}}}} \right)}^3}}}{{3{w_j}}}} $ | (7) |
当dσ2/dtd=0时,td=tj-1+wj/2,标准差最小,σ2=wj2/12,因此定义tj为
| $ {t_j} = \sum\limits_{k = 0}^{j - 1} {{w_k} + \frac{{{w_j}}}{2}} $ | (8) |
等效标准差即为
| $ \sigma _{{\rm{eq}}}^2 = \sum\limits_{i = 1}^n {\frac{{w_i^2{w_i}}}{{12{T_{{\rm{clk}}}}}}\left( {{T_{{\rm{clk}}}} = \sum {{w_i}} } \right)} $ | (9) |
通过测量可知,最低有效位(LSB,least significant bit)用于表征双链三路TDC的测量分辨率,数值为5.63 ps.当输入时间间隔数据为120 ns时,RMS精度为11.7 ps(27 ℃).
2.2 TDC非线性分析图 7(a)显示了码密度方案测试结果,为做全面分析,将单链单路TDC、单链三路TDC和双链三路TDC共同比较.后两者显然有效提升了测量分辨率. DNL和INL为
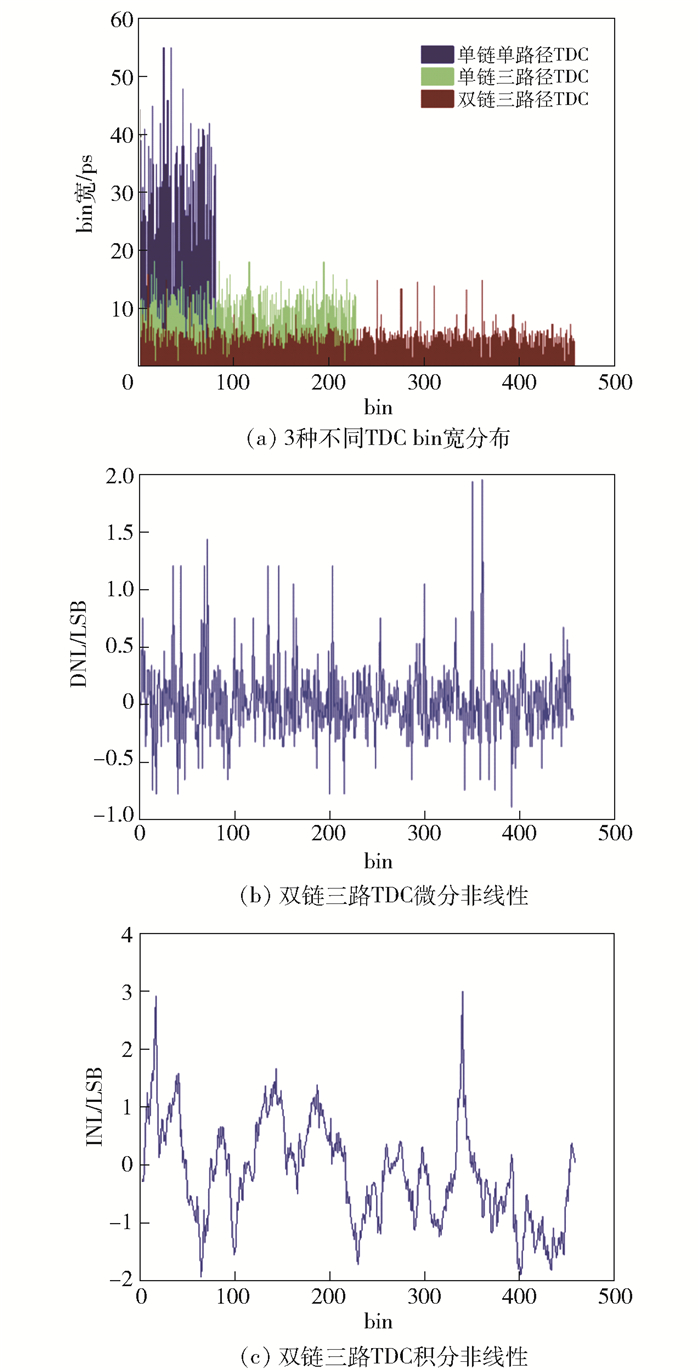
|
图 7 TDC电路参数测试结果 |
| $ \left. {\begin{array}{*{20}{l}} {D{{\left[ k \right]}_{{\rm{DNL}}}} = \frac{{\left( {w\left[ k \right] - Q} \right)}}{Q}}\\ {I{{\left[ k \right]}_{{\rm{INL}}}} = \sum\limits_{n = 0}^k {D{{\left[ k \right]}_{{\rm{DNL}}}}} } \end{array}} \right\} $ | (10) |
其中:Q为理想bin宽值,W[k]为实际测量值.由图 7可知,DNL为[-0.79, 1.87] LSB (-4.45~10.53 ps),INL为[-1.94, 3.04] LSB (-10.92~17.12 ps). RAM预先存储所有bin数据值,完成在线校准[11].
经测试,由表 1可知,六链并行TDC的等效分辨率为5.87 ps,RMS测量精度为10.4 ps;双链三路TDC在分辨率、RMS精度、DNL/INL等指标上同样性能优良,相比于六链并行TDC,该电路占用的FPGA逻辑资源降低约43.1%,进而降低了芯片功耗,功耗降低约36.8%.
|
|
表 1 六链并行TDC与双链三路TDC的性能对比 |
TDC中的bin宽受温度的影响而改变,这种改变来源于载流子迁移率的变化.由式(2)可知,延时单元的总延时由4部分构成,迁移率上升,电路载流子漂移速度上升,电容充放电延时下降,延时单元的延时时间随之缩短,TDC的bin宽(Bw)与迁移率存在关系:
| $ {B_{\rm{w}}}\left( T \right) \propto \frac{1}{\mu } \propto \frac{{{N_i}}}{{{T^{3/2}}}} + {N_{\rm{s}}}{T^{3/2}} + \frac{{{N_{\rm{o}}}}}{{\exp \left( {\frac{{\hbar {\omega _l}}}{{{k_0}T}}} \right) - 1}} $ | (11) |
其中:Ni、Ns和No为常数,T为绝对温度,k0为玻耳兹曼常数,ħ为约化普朗克常数,ωl为光波角频率.在Artix_7系列FPGA中,调用赛灵思模数转换器(XADC, Xilinx analog to digital converter)模块,可以有效检测FPGA芯片温度. XADC模块中集成了温度传感器,以5 ℃为测量步长,等效bin宽与温度近似线性相关,当温度从5 ℃上升到85 ℃时,等效bin宽由5.69 ps降低至5.47 ps.由式(8)可知,时间测量中,bin宽数值的累加,导致测量误差增大.
为完成测量修正,设计温度补偿方案.引入温度校准系数Cof完成测量修正.由测试结果图 8(a)可知,校准系数Cof与温度近似线性相关:
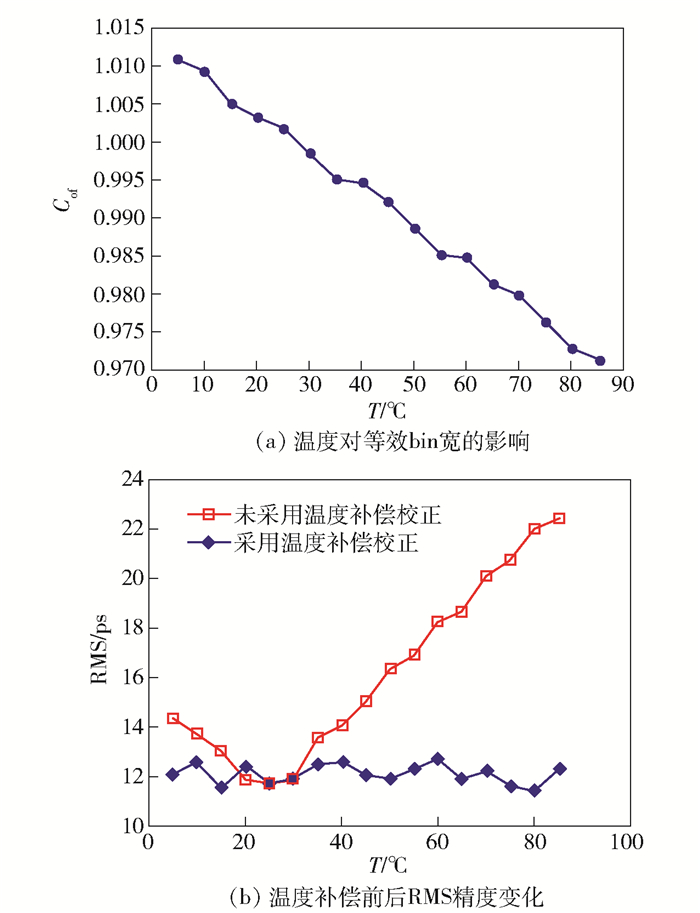
|
图 8 TDC温度校正分析 |
| $ \begin{array}{c} {C_{{\rm{of}}}} = 1.013 - 0.00049T\\ {T_j} = {C_{{\rm{of}}}}{t_j} \end{array} $ | (12) |
其中:tj为原始时间测量数据,Tj为修正后的测量数据.当温度为27 ℃(300 K)时,Cof=1,等效bin宽为5.63 ps.经过校准,温度从5 ℃变化至85 ℃,如图 8(b)所示,RMS精度显著优化.
3 结束语TDC的指标直接决定激光雷达的参数性能,基于低成本Artix-7系列FPGA设计双链三路TDC,具有高分辨率、RMS精度高、可温度补偿等优势.使用6个数据表征TDC测量值,等效分辨率提升至5.63 ps.流水线编码电路可有效提高逻辑资源利用率,采用码密度方案逐一确定bin宽的精确值和等效分辨率.调用FPGA中的XADC模块测量芯片温度,在5~85 ℃的温度范围内,完成补偿修正,RMS精度显著优化.相比于六链延迟线TDC,双链三路TDC具有相近的指标参数,并使FPGA逻辑资源使用率降低了43.1%,芯片功耗降低了36.8%.该工作为其他系列FPGA设计TDC提供了技术参考.
| [1] |
Xu Zhongyang, Tang Liangzun, Zhang Hongxiang, et al. Simultaneous real-time ranging and velocimetry via a dual-sideband chirped lidar[J]. IEEE Photonics Technology Letters, 2017, 29(24): 2254-2257. DOI:10.1109/LPT.2017.2771415 |
| [2] |
尹俊, 倪发福, 张建川, 等. 基于FPGA与GPS的时间测量电路设计与实现[J]. 原子能科学技术, 2019, 53(1): 151-157. Yin Jun, Ni Fafu, Zhang Jianchuan, et al. Design and realization of time measurement based on FPGA and GPS[J]. Atomic Energy Science and Technology, 2019, 53(1): 151-157. |
| [3] |
Bayer E, Traxler M. A high-resolution (< 10 ps RMS) 48-channel time-to-digital converter(TDC) implemented in a field programmable gate array(FPGA)[J]. IEEE Transactions on Nuclear Science, 2011, 58(1): 1547-1552. |
| [4] |
Pan Weibin, Gong Guanghua, Li Jianmin. A 20-ps time-to-digital converter(TDC) implemented in field-programmable gate array (FPGA) with automatic temperature correction[J]. IEEE Transactions on Nuclear Science, 2014, 6(3): 1468-1473. |
| [5] |
Shen Qi, Liu Shubin, Qi Binxiang, et al. A 1.7 ps equivalent bin size and 4.2 ps RMS FPGA TDC based on multichain measurements averaging method[J]. IEEE Transactions on Nuclear Science, 2015, 62(3): 947-954. DOI:10.1109/TNS.2015.2426214 |
| [6] |
Chen Haochang, Zhang Yongliang, David Day-Uei Li. A low nonlinearity missing-code free time-to-digital converter based on 28-nm FPGAs with embedded bin width calibrations[J]. IEEE Transactions on Instrumentation & Measurement, 2017, 66(7): 1912-1921. |
| [7] |
王丹, 王健, 来金梅. 一种基于FPGA快速进位链的时间数字转换电路[J]. 复旦大学学报(自然科学版), 2016, 55(1): 59-67. Wang Dan, Wang Jian, Lai Jinmei. A FPGA-based time-to-digital converter(TDC) using carry chains[J]. Journal of Fudan University (Natural Science), 2016, 55(1): 59-67. |
| [8] |
Jan M Rabaey, Anantha C. Digital integrated circuits:a design perspective[M]. Second Edition. Beijing: Publishing House of Electronics Industry, 2004: 313-316.
|
| [9] |
Zhao Lei, Hu Xueye, Liu Shubin, et al. The design of a 16-channel 15 ps TDC implemented in a 65 nm FPGA[J]. IEEE Transactions on Nuclear Science, 2013, 60(5): 3532-3536. DOI:10.1109/TNS.2013.2280909 |
| [10] |
Wang Yonggang, Kuang Jie, Liu Chong, et al. A 3.9-ps RMS precision time-to-digital converter using ones-counter encoding scheme in a Kintex-7 FPGA[J]. IEEE Transactions on Nuclear Science, 2017, 64(10): 2713-2718. DOI:10.1109/TNS.2017.2746626 |
| [11] |
Liu Chong, Wang Yonggang. A 128-channel, 710M samples/second, and less than 10 ps RMS resolution time-to-digital converter implemented in a Kintex-7 FPGA[J]. IEEE Transactions on Nuclear Science, 2013, 62(3): 773-783. |


