2. 北京空间飞行器总体设计部 空间智能机器人系统技术与应用北京市重点实验室, 北京 100094
针对复杂接触环境下机器人柔顺装配困难的问题,提出了一种基于受力信息精准获取与改进力/位混合控制算法的柔顺装配方法.在对机器人末端力传感器进行零点补偿及负载重力补偿后,通过矩阵变换实时计算出装配接触点处机器人末端执行器的真实受力,并在力控制过程中让机器人的运动遵循双曲正切速度-力关系.实验结果表明,机器人在装配过程中并未发生明显的抖动,所提算法具有良好的柔顺装配效果.
2. Beijing Key Laboratory of Intelligent Space Robotic Systems Technology and Applications, Beijing Institute of Spacecraft System Engineering, Beijing 100094, China
Aiming at the problem that the difficulty of compliant assembly of robot in complex contact environments, a compliant assembly method based on accurate acquisition of force information and improved hybrid force/position control algorithm is presented.In the method, after bias and load gravity compensation are performed on the robot end force sensor, the real contact force of the robot end-effector at the assembly contact point is calculated in real time by matrix transformation, and the motion of the robot follows velocity-force relationship of the hyperbolic tangent during force control.Experiments show that the robot did not shake significantly during the assembly process, and the proposed algorithm has a good compliant assembly effect.
目前,机械臂在工业生产和技术研究中发挥的作用越来越大,常常被应用在装配、焊接及搬运等场合,但这些场合大都是一些作业任务相对简单、工作环境相对稳定的场合,机械臂从事的也多是些重复性或者预先规划好的动作,一旦面对复杂的作业任务,机械臂的完成度并不太理想.在航天事业中,对机械臂的需要及要求越来越高[1],机械臂要求在无人环境或远程控制下,自主完成对航天器部件的安装及更换,这需要机械臂与航天器之间具有很好的柔顺装配能力[2-3].
柔顺控制就是从力传感器取得控制信号,用此信号去控制机械臂的运动,常用的柔顺控制方法有阻抗控制[4-5]、力位混合控制[6-8]等.柔顺控制的目的主要有2个:其一,防止机械臂与环境接触时发生过大的接触力,导致机械臂或被接触物体发生损害;其二,有些作业任务确实需要机械臂根据受力感知不断调整两者之间的相对位姿关系,否则无法完成任务.现有的柔顺装配技术并不成熟,在面对大负载、被装配物自身具有一定柔性、装配接口复杂等情况,任务的成功率会大大降低.
柔顺装配的成功与否与两方面因素息息相关:其一,获取的力/力矩信息是否精准;其二,力柔顺控制策略是否符合任务需要.柔顺装配要用到六维力传感器,由于六维力传感器自身的设计结构,会存在维间耦合的问题,所以需要解耦以最大程度上减小或消除耦合干扰.通常的解耦方法是采用基于最小二乘法的静态线性解耦[9],获得解耦矩阵,随着人工智能领域的兴起,神经网络算法被应用在了六维力传感器的非线性解耦问题上,并取得了显著的效果[10].采用直接购置的ATI OMEGA191六维力传感器进行数据采集,此六维力传感器在出厂前经过标定,耦合误差小于满量程(F.S.,full scale)的0.5%,因此不再需要对此六维力传感器进行重新标定.解耦后的六维力传感器仍然会存在自身的系统误差,即在空载状况下六维力传感器的读数不为零.此误差也被称之为传感器的零点,负载的大小及与传感器的紧固方式会对六维力传感器的零点产生影响,因此,在柔顺装配中为获取精准的外部接触力/力矩信息,还需要在负载状况下对六维力传感器进行零点补偿和负载重力补偿.在传感器的零点补偿方面,通过调整机器人至一系列特殊姿态就可以进行计算,Vougioukas等[11-13]对其进行了研究;对于负载重力补偿方面,通过计算机器人安装倾角、负载重心坐标及负载重力大小等参数,可以消除负载重力对力传感器的影响,张立建等[13-16]对其进行了研究.理想状态下,在对六维力传感器进行零点补偿和负载重力补偿后,所得到的力/力矩信息是负载受到外部接触力后,六维力传感器感知到的自身受到的力/力矩信息,依据此时的力/力矩信息,可以实现力柔顺控制,但机械臂末端工具是各式各样的,受力环境是复杂的,相比于六维力传感器处的受力感知,工具末端的直接接触点处的受力信息更能真实反映负载的受力情况,依据此数据进行柔顺控制,这对于提高力柔顺控制的精准性是有利的.另外,对于力柔顺控制中所构建的速度—力关系,一般采用线性关系,胡瑞钦等[17]将速度—力的关系构建成了“S”形曲线函数,这对于避免在接触力异常大的情况下机械臂自身发生震荡具有良好的效果,但公式过于复杂.
笔者从力/力矩信息的精准获取和力柔顺控制策略两方面入手对机械臂的柔顺装配技术进行了研究.通过对六维力传感器数据的进一步处理,得到了机械臂末端工具接触点处的力/力矩信息,在此基础上,借鉴双曲正切曲线构建了接触点处的力-速度曲线函数,并将之融入到基于速度的力/位混合控制中.最后,在视觉引导下,采用KUKA机械臂对在轨可更换单元(ORU,orbital replaceable unit)模型与星体模型的装配过程进行了力柔顺控制,验证了所提算法的可行性.
1 接触点处受力信息的计算机器人腕部六维力传感器测得的力与力矩数据理论上由3部分组成,即传感器自身系统误差、负载重力作用及负载所受外部接触力对传感器的作用.若要精确得到负载所受外部接触力对传感器的影响,需要对此六维力传感器测量数据进行传感器零点补偿及负载重力补偿,具体的实施步骤可参考文献[13].六维力传感器经过零点补偿及负载重力补偿后的数据并不等于机械臂工具末端与工件的直接接触力信息,为提高力柔顺控制的精准性,还需要根据机械臂末端工具情况对此数据做进一步计算,以得到接触点处直接接触力/力矩.
由于机械臂末端工具的不同,计算直接接触力的方式也不同,末端工具可分为3类,如图 1所示.

|
图 1 机械臂末端工具 |
由图 1可以看出,上述3种情况都是轴孔装配的情况. 图 1(a)类末端工具最简单,只是单一输出轴,且方向与力传感器坐标系Z方向一致;图 1(b)类末端工具有多个输出轴,多个输出轴相互平行,且方向与力传感器坐标系Z方向一致,这意味着装配中末端工具同时会有多个点与被装配物体发生接触,与图 1(a)类情况相比,增加了装配的难度;图 1(c)类末端工具的轴线指向任意,与力传感器中心轴线无论在位置上还是角度上都不统一,最难精确实现实时力柔顺控制.
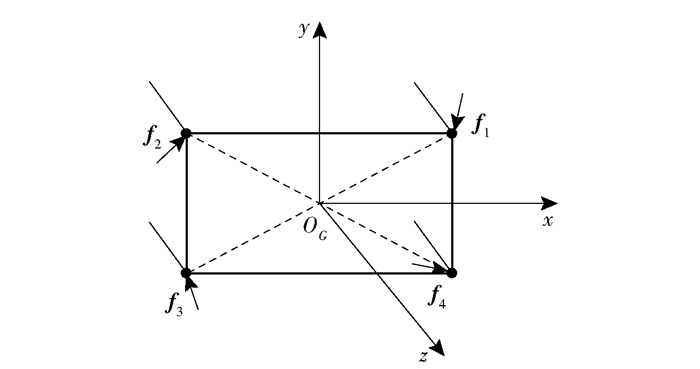
对以上3种机械臂末端工具进行分析,寻找计算接触点处直接接触力/力矩的方法.对于图 1(a)情况,处理起来最为简单,可以在工具末端接触点处建立一个方向与力传感器坐标系方向相同的坐标系,将力传感器的力/力矩数据经简单计算转化成工具末端的力/力矩信息.对于图 1(b)的情况,由于存在多个力接触点,根据力传感器实时获得的力/力矩信息,很难分别计算每个力接触点处的受力情况,另外,同时对多个受力点进行力控也相当困难,因此,只需处理几个接触点所受力的合力/合力矩.如图 2所示,几个力接触点形成一个共面,在共面的中心点OG处建立末端工具坐标系OG-xyz,坐标系各方向与力传感器坐标系OL-XYZ方向一致,几个接触点处的力f1、f2、f3及f4会在OG处形成一合力,投影到x、y、z三个方向分别是fx、fy及fz.
|
图 2 多个力接触点的末端工具示意图 |
因此,在计算机械臂末端工具接触点处的受力时,将图 1(b)和(a)的情况用同一种方法处理.对于图 1(a)和(b)的情况,工具末端与力传感器之间的坐标关系如图 3所示.其中,OL-XYZ是力传感器的坐标系,OG-xyz是工具末端的坐标系,两坐标系姿态一致,只有原点位置的偏差.

|
图 3 力传感器与工具末端的坐标关系 |
假定工具末端各方向所受力/力矩分别为[fx, fy, fz, mx, my, mz],经过传感器零点补偿及负载重力补偿后的力传感器所受力/力矩分别为[FX, FY, FZ, MX, MY, MZ],则可知
| $ \left. {\begin{array}{*{20}{l}} {{f_x} = {F_X}}\\ {{f_y} = {F_Y}}\\ {{f_z} = {F_Z}} \end{array}} \right\} $ | (1) |
假定工具末端坐标系原点OG在力传感器坐标系OL-XYZ下的坐标为{xG, yG, zG},则工具末端所受力对力传感器的力矩可为
| $ \left. {\begin{array}{*{20}{c}} {{M_{{X_1}}}}&{ = {f_z}{y_G} - {f_y}{z_G}}\\ {{M_{{Y_1}}}}&{ = {f_x}{z_G} - {f_z}{x_G}}\\ {{M_{{Z_1}}}}&{ = {f_y}{x_G} - {f_x}{y_G}} \end{array}} \right\} $ | (2) |
其中MX1、MY1及MZ1分别为末端工具所受力对力传感器X、Y、Z轴的力矩.针对图 1(a)和(b)情况,末端工具所受力矩为
| $ \left. {\begin{array}{*{20}{l}} {{m_x} = {M_X} - {M_{{X_1}}}}\\ {{m_y} = {M_Y} - {M_{{Y_1}}}}\\ {{m_z} = {M_Z} - {M_{{Z_1}}}} \end{array}} \right\} $ | (3) |
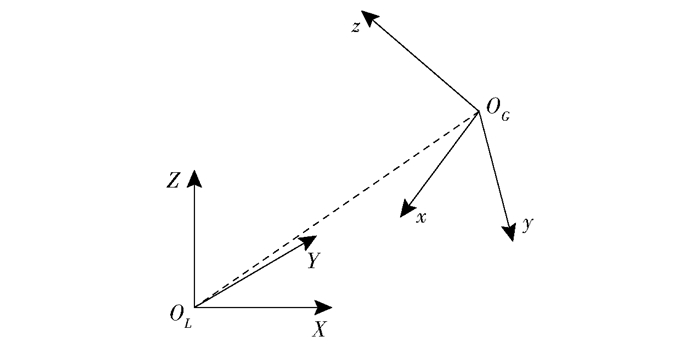
对图 1(c)的情况,工具末端坐标系OG-xyz与力传感器坐标系OL-XYZ的关系如图 4所示,工具末端坐标系相对力传感器坐标系的位姿矩阵为GLT.
|
图 4 工具末端与力传感器关系图 |
假定
| $ _G^L\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{x_G}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{y_G}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{z_G}}\\ 0&0&0&1 \end{array}} \right] $ | (4) |
力传感器各方向所受到的力为工具末端所受到的力在力传感器坐标系3个方向的投影合力,关系为
| $ \left[ {\begin{array}{*{20}{c}} {{F_X}}\\ {{F_Y}}\\ {{F_Z}} \end{array}} \right] = _G^L\mathit{\boldsymbol{R}}\left[ {\begin{array}{*{20}{c}} {{f_x}}\\ {{f_y}}\\ {{f_z}} \end{array}} \right] $ | (5) |
可求得工具末端各方向所受力[fx, fy, fz],而工具末端所受力对力传感器的力矩计算如下:
| $ \left. {\begin{array}{*{20}{l}} {{M_{{X_1}}} = {F_Z}{y_G} - {F_Y}{z_G}}\\ {{M_{{Y_1}}} = {F_X}{z_G} - {F_Z}{x_G}}\\ {{M_{{Z_1}}} = {F_Y}{x_G} - {F_X}{y_G}} \end{array}} \right\} $ | (6) |
将OL-XYZ坐标系移到工具末端点OG处,形成一新的坐标系OG-XYZ,则对于工具末端点OG,所受到的绕X、Y、Z 3个方向的力矩为
| $ \left. {\begin{array}{*{20}{l}} {{m_X} = {M_X} - {M_{{X_1}}}}\\ {{m_Y} = {M_Y} - {M_{{Y_1}}}}\\ {{m_Z} = {M_Z} - {M_{{Z_1}}}} \end{array}} \right\} $ | (7) |
则对于工具末端点OG,所受到的绕x、y、z 3个方向的力矩为
| $ \left[ {\begin{array}{*{20}{c}} {{m_x}}\\ {{m_y}}\\ {{m_z}} \end{array}} \right] = _G^L{\mathit{\boldsymbol{R}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{m_X}}\\ {{m_Y}}\\ {{m_Z}} \end{array}} \right] $ | (8) |
针对图 1所示的3种末端工具的情况,通过上述方法对力传感器数据进行了计算,得到了工具末端力接触点处所受到的实时力/力矩.
2 力柔顺控制策略研究针对工具末端接触点处受到的实时力/力矩信息,需要对其进行处理,以得到相应自由度上的速度或角速度.在机械臂末端工具与物体发生较大的力接触时,机械臂的反应速度应该要快一点,以尽快减小受力.但在某些情况下接触点处力的值异常大时,为减小抖动,机械臂的反应速度不应该随受力值呈线性增长.因此,为解决这一问题,借助双曲正切函数给出了机械臂末端的速度—力曲线.
| $ \mathit{\boldsymbol{v}} = h(\mathit{\boldsymbol{f}}) = b{\rm{tanh}}(\mathit{\boldsymbol{f}}/a) $ | (9) |
其中:f为工具末端点所受到的力/力矩[fx, fy, fz, mx, my, mz];a、b为常数,可根据具体情况对其进行赋值;v为在外力作用下工具末端点处的速度、角速度.
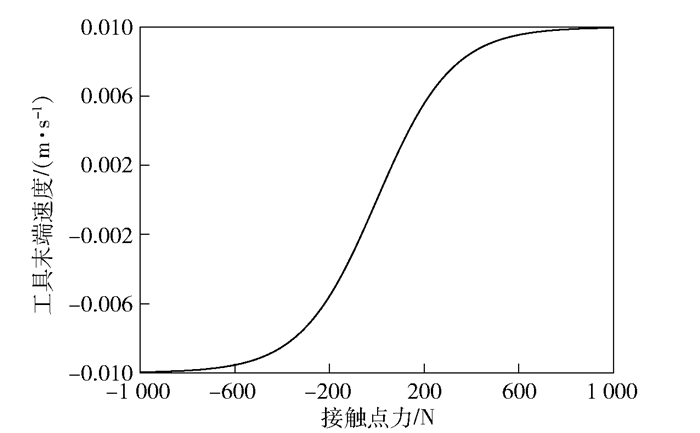
在外力作用下,工具末端点的速度—力曲线是一条“S”形曲线,例如,给常数a、b赋值,假定a=1 000/π,b=1/100,则曲线如图 5所示.
|
图 5 速度—力曲线 |
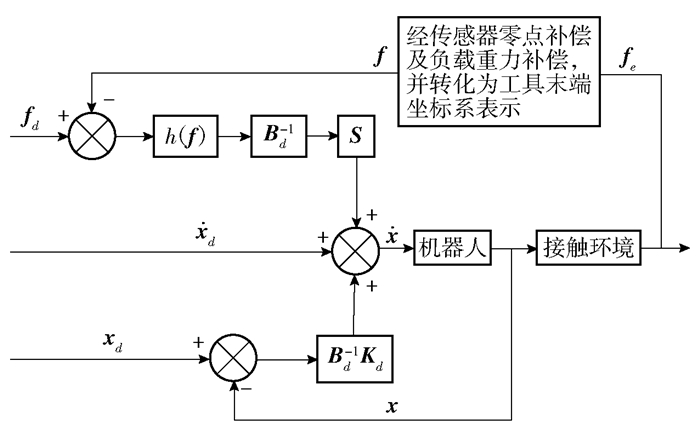
针对机械臂装配过程中的力柔顺问题,采用的是基于速度的力/位混合控制算法,如图 6所示.
|
图 6 基于速度的力/位混合控制 |
则机械臂工具末端速度为
| $ \mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{\dot x}}_d} + \mathit{\boldsymbol{B}}_d^{ - 1}{\mathit{\boldsymbol{K}}_d}({\mathit{\boldsymbol{x}}_d} - \mathit{\boldsymbol{x}}) + \mathit{\boldsymbol{SB}}_d^{ - 1}h({\mathit{\boldsymbol{f}}_d} - \mathit{\boldsymbol{f}}) $ | (10) |
其中:
在视觉引导下采用KUKA机械臂来进行ORU模型与星体模型的力柔顺装配演示验证实验,如图 7所示,操作步骤如下:

|
图 7 力柔顺装配实验 |
1) ORU安装在星体上,在力控模式下,视觉引导机械手完成对ORU的抓取;
2) 在力控模式下完成ORU与星体间的主动解锁;
3) 机械臂抓持ORU远离星体后,又在视觉引导下靠近星体,在力控模式下完成与星体的自主对接;
4) 机械臂末端手爪对ORU的适配器进行释放,机械臂退到指定位置.
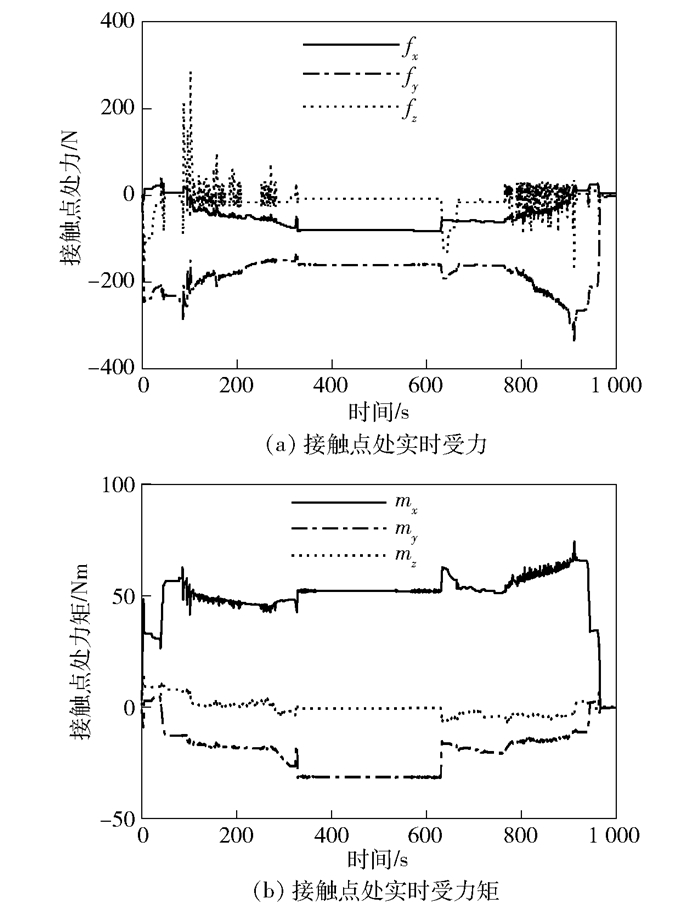
在ORU模型与星体模型的力柔顺装配演示验证任务中,末端工具接触点处实时受力及受力矩如图 8所示.
|
图 8 装配过程中的实时力/力矩信息 |
ORU模型与星体模型的力柔顺装配演示验证实验的运行大约需要16 min,整个过程中,接触点处所受力最大不超过400 N,所受力矩最大不超过80 Nm,力接触点处所受力/力矩均在安全范围之内.力/力矩的峰值及剧烈变化发生在末端手爪抓取ORU以及ORU与星体间的主动解锁与对接的过程中,机器人在装配过程中未发生剧烈抖动现象,整个力柔顺装配过程比较顺利.
4 结束语针对工业机械臂在柔顺装配方面遇到的问题,提出了一种直接计算接触点处受力信息的方法,将六维力传感器采集的信息转化为工具末端接触点处的力信息,更能反映装配过程中力接触的真实情况.借鉴双曲正切函数,提出了一种柔顺控制中的机械臂末端速度—力曲线函数,并将之融入基于速度的力/位混合控制算法中.在视觉引导下,采用KUKA机械臂对ORU模型与星体模型的装配进行了柔顺控制演示验证实验,验证了所提算法的可行性.
| [1] |
Li Weijie, Cheng Dayi, Liu Xigang, et al. On-orbit service (OOS) of spacecraft:a review of engineering developments[J]. Progress in Aerospace Sciences, 2019, 108: 32-120. DOI:10.1016/j.paerosci.2019.01.004 |
| [2] |
邓雅, 刘维惠, 李晓辉, 等. 一种空间机械臂无视觉在轨柔顺装配方法[J]. 空间控制技术与应用, 2018, 44(6): 8-12. Deng Ya, Liu Weihui, Li Xiaohui, et al. Space manipulator compliant on-orbit assembly without vision feedback[J]. Aerospace Control and Application, 2018, 44(6): 8-12. |
| [3] |
Dai F, Wahrburg A, Matthias Björn, et al. Robot assembly skills based on compliant motion[C]//Proceedings of ISR 2016: 47th International Symposium on Robotics. Munich: VDE, 2016: 1-6.
|
| [4] |
任珊珊.空间柔性机械臂接触操作动力学分析及阻抗控制策略研究[D].北京: 北京邮电大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10013-1017289099.htm
|
| [5] |
Kim S, Kim J P, Ryu J. Adaptive energy-bounding approach for robustly stable interaction control of impedance-controlled industrial robot with uncertain environments[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(4): 1195-1205. DOI:10.1109/TMECH.2013.2276935 |
| [6] |
Chaudhary H, Panwar V, Prasad R, et al. Adaptive neuro fuzzy based hybrid force/position control for an industrial robot manipulator[J]. Journal of Intelligent Manufacturing, 2016, 27(6): 1299-1308. DOI:10.1007/s10845-014-0952-1 |
| [7] |
常健, 王亚珍, 李斌. 基于力/位混合算法的7自由度机械臂精细操控方法[J]. 机器人, 2016, 38(5): 531-539. Chang Jian, Wang Yazhen, Li Bin. Accurate operation control method based on hybrid force/position algorithm for 7-DOF manipulator[J]. Robot, 2016, 38(5): 531-539. |
| [8] |
陈钢, 王玉琦, 贾庆轩, 等. 机器航天员轴孔装配过程中的力位混合控制方法[J]. 宇航学报, 2017, 38(4): 410-419. Chen Gang, Wang Yuqi, Jia Qingxuan, et al. Hybrid force and position control strategy of robonaut performing peg-in-hole assembly task[J]. Journal of Astronautics, 2017, 38(4): 410-419. |
| [9] |
徐科军, 李成. 多维腕力传感器静态解耦的研究[J]. 合肥工业大学学报(自然科学版), 1999(2): 3-8. Xu Kejun, Li Cheng. Research on static decoupling for multi-dimensional wrist force sensor[J]. Journal of Hefei University of Technology, 1999(2): 3-8. |
| [10] |
李映君, 韩彬彬, 王桂从, 等. 基于径向基函数神经网络的压电式六维力传感器解耦算法[J]. 光学精密工程, 2017, 25(5): 1266-1271. Li Yingjun, Han Binbin, Wang Guicong, et al. Decoupling algorithms for piezoelectric six-dimensional force sensor based on RBF neural network[J]. Optics and Precision Engineering, 2017, 25(5): 1266-1271. |
| [11] |
Vougioukas S. Bias estimation and gravity compensation for force-torque sensors[C]//Proceedings of 3rd WSEAS Symposium on Mathematical Methods and Computational Techniques in Electrical Engineering. Athens: WSEAS Press, 2001: 82-85.
|
| [12] |
林君健.基于力传感器的工业机器人主动柔顺装配系统研究[D].广州: 华南理工大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10561-1013319416.htm
|
| [13] |
张立建, 胡瑞钦, 易旺民. 基于六维力传感器的工业机器人末端负载受力感知研究[J]. 自动化学报, 2017, 43(3): 439-447. Zhang Lijian, Hu Ruiqin, Yi Wangmin. Research on force sensing for the end-load of industrial robot based on a 6-axis force/torque sensor[J]. Acta Automatica Sinica, 2017, 43(3): 439-447. |
| [14] |
Massa D, Callegari M, Cristalli C. Manual guidance for industrial robot programming[J]. Industrial Robot:an International Journal, 2015, 42(5): 457-465. DOI:10.1108/IR-11-2014-0413 |
| [15] |
张光辉, 王耀南. 末端F/T传感器的重力环境下大范围柔顺控制方法[J]. 智能系统学报, 2015, 10(5): 675-683. Zhang Guanghui, Wang Yaonan. A wide range compliance control method in gravity environment based on end force/torque sensor[J]. CAAI Transactions on Intelligent Systems, 2015, 10(5): 675-683. |
| [16] |
吴航.搬运装配机器人主动柔顺技术研究与应用软件开发[D].南京: 东南大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10286-1018037842.htm
|
| [17] |
胡瑞钦, 张立建, 孟少华, 等. 基于柔顺控制的航天器大部件机器人装配技术[J]. 机械工程学报, 2018, 54(11): 85-93. Hu Ruiqin, Zhang Lijian, Meng Shaohua, et al. Robotic assembly technology for heavy component of spacecraft based on compliance control[J]. Journal of Mechanical Engineering, 2018, 54(11): 85-93. |



