2. 中国科学院大学 电子电气与通信工程学院, 北京 100049
针对低密度奇偶校验(LDPC)码的译码算法复杂度和译码性能的均衡,为了提高译码算法的可靠性和适用性,在自纠正最小和(SCMS)算法的基础上,提出了一种动态自纠正最小和(DSCMS)算法.该算法在迭代译码的过程中,根据变量节点消息设置阈值,明确了SCMS算法中对消息可靠性的判断,提高了算法的误码特性和收敛特性.仿真结果表明,所提出的DSCMS算法的误码性能和收敛性能都要优于SCMS算法及其改进算法.当编码效率为1/2时,DSCMS算法与SCMS算法相比,最多能降低7.15%的迭代次数.
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
Aiming at the trade-off between the decoding complexity and the decoding performance of low-density parity check (LDPC) codes, and improving the reliability and applicability of the decoding algorithm, a dynamic self-corrected minimum sum(DSCMS)algorithm is proposed based on the self-corrected minimum sum(SCMS)algorithm. In the process of iterative decoding, the algorithm sets the threshold according to the variable node message, clarifies the judgement of the message reliability in SCMS, and improves the error characteristics and convergence characteristics of the algorithm. Simulation results show that the error performance and convergence performance of DSCMS are better than those of SCMS. When the coding rate is 1/2, the number of iterations of DSCMS can be reduced by up to 7.15% compared with SCMS.
差错控制编码是提高信息传输可靠性的一种关键技术,是大多数现代数字通信系统和数据存储系统不可或缺的重要部分[1-2].低密度奇偶校验(LDPC,low-density parity-check)码在1962年被Gallager博士首先提出,是一类具有很强纠错能力的编码技术[3].由于LDPC码具有描述简单、译码复杂度低、可并行实现、使用灵活、误码平层低等优点,在实际系统中得到了广泛的应用,并被第5代移动通信系统的新无线电(NR, new radio)采纳为增强型移动宽带(eMBB, enhanced mobile broadband)场景中数据信道的长码编码方案[4-5].
LDPC码在最初被Gallager提出的时候并没有引起人们的重视,由于当时硬件技术的限制,长码的译码实现起来非常困难.到了20世纪90年代,MacKay和Neal[6]证明了在与置信传播(BP, belief propagation)的迭代译码相结合的条件下,LDPC码具有逼近Shannon限的性能,LDPC码也因此逐渐成为学术界研究的热点. BP算法的缺点是计算复杂度高,尤其是在消息量化比特较低时性能严重下降. Fossorier[7]在此基础上,将校验节点消息计算公式进行简化,用比较运算代替了查找表运算,提出了最小和(MS, minimum sum)算法. MS算法虽然降低了计算复杂度,但译码性能有较大的损失.后来Chen等[8-9]提出了偏移最小和(OMS, offset minimum sum)算法和归一化最小和(NMS, normalized minimum sum)算法,分别通过减法和除法修正校验节点的消息,获得了逼近BP算法的译码性能,同时计算复杂度接近最小和算法.近年来,Savin等[10-12]提出了自纠正最小和(SCMS, self-corrected minimum sum)算法及其改进算法,从变量节点消息的角度出发,提高了译码性能,并且加快了译码的收敛性.
SCMS算法具有准最佳译码性能,但它只是将变量节点消息的符号改变作为判断消息不可靠的依据,没有明确说明如何判断消息的可靠性,并且在信噪比较高的情况下,SCMS算法的收敛性下降明显.为了进一步提高LDPC码的译码可靠性与收敛性,在SCMS算法的基础上,提出了一种动态自纠正最小和(DSCMS,dynamic self-corrected minimum sum)译码算法,该算法可以根据信道情况,在迭代译码的过程中,通过改变阈值的大小,动态调整消息可靠性的判断,提高译码性能,加快译码收敛性,同时也提高了系统的灵活性.
1 BP算法最原始的BP算法,也称为概率阈BP算法,在变量节点和校验节点之间传递的信息是节点取特定值的概率.此译码算法采用了很多相乘计算,需要耗费较多译码时间和硬件资源,不容易在工程上实现.因此,将算法中的概率运算转换到对数域中,即对数似然比(LLR, log-likelihood ratio)BP算法[13].这样就能够把更多复杂的乘法运算简化成简单的加法运算,在很大程度上降低了BP译码算法中迭代更新运算的复杂度.为了便于后面描述,相关变量符号的定义如下:H表示LDPC码的校验矩阵,其对应的Tanner图中,包含N个变量节点和M个校验节点;i代表H中的一个变量节点,i∈{1, 2, …, N};j代表H中的一个校验节点,j∈{1, 2, …, M};C(i)表示与变量节点i相连的校验节点的集合;R(j)表示与校验节点j相连的变量节点的集合;C(i)\j表示除j外与变量节点i相连的校验节点的集合;R(j)\i表示除i外与校验节点j相连的变量节点的集合;L(Pi)信道初始概率似然比消息;L(rji)表示校验节点消息(变量节点i传向校验节点j的外部概率似然比消息);L(qij)表示变量节点消息(校验节点j传向变量节点i的外部概率似然比消息);L(qi)表示判决量消息(变量节点i收集到的所有消息);
LLR BP算法的步骤可以概括如下.
1) 初始化
根据测试需要,设置最大迭代次数,计算信道传递给变量节点的初始概率似然比消息L(Pi),然后对每一个变量节点i和与其相邻的校验节点j∈C(i),初始化变量节点消息
| $ {L^{(0)}}({q_{ij}}) = L({P_i}) $ | (1) |
将所有校验节点消息的初始值设置为零.
2) 迭代处理
步骤1 校验节点消息处理
对所有的校验节点j和与其相邻的变量节点i∈R(j),第l次迭代时,计算校验节点消息
| $ {L^{(l)}}({r_{ji}}) = 2{\rm{tan}}{{\rm{h}}^{ - 1}}\left\{ {\prod\limits_{{i^\prime } \in {R_j}\backslash i} {{\rm{tanh}}\left[ {\frac{1}{2}{L^{(l - 1)}}({q_{{i^\prime }j}})} \right]} } \right\} $ | (2) |
步骤2 变量节点消息处理
对所有的变量节点i和与其相邻的校验节点j∈C(i),第l次迭代时,计算变量节点消息:
| $ {L^{(l)}}({q_{ij}}) = L({P_i}) + \sum\limits_{{j^\prime } \in {C_i}\backslash j} {{L^{(l)}}({r_{{j^\prime }i}})} $ | (3) |
步骤3 译码判决
对所有变量节点计算判决量消息
| $ {L^{(l)}}({q_i}) = L({P_i}) + \sum\limits_{j \in {C_i}} {{L^{(l)}}} ({r_{ji}}) $ | (4) |
判决规则:若L(l)(qi)>0,则
3) 停止
若
虽然LLR BP算法已经在概率域BP算法的基础上简化了很多运算,但是其校验节点的更新计算中含有双曲正切函数及其反函数,在实现上依然很复杂,因此Fossorier[7]对其进行简化,提出了MS算法.
2.1 MS算法MS算法的简化原理:因为tanh x、tanh-1x都是奇函数,tanh |x|在0~1之间取值,并且是|x|的单调递增函数,故MS算法校验节点的更新计算可以表示为
| $ L({r_{ji}}) = \prod\limits_{{i^\prime } \in {R_j}\backslash i} {{\rm{sgn}}} [L({q_{{i^\prime }j}})]\mathop {{\rm{min}}}\limits_{{i^\prime } \in {R_j}i} [|L({q_{{i^\prime }j}})|] $ | (5) |
MS算法是LLR BP算法的一种近似,在校验节点的更新中,使用最小值和次小值代替了要传递的置信度消息.这种近似替代牺牲了一部分性能,但大大降低了硬件复杂度,实现过程中,只有“求和”运算和“比较”运算.
比较式(2)与式(5)可以发现,近似后的表达式中,符号与原来一致,而幅度大于原来的值.基于此,Chen等[8]提出了NMS算法和OMS算法,来修改增加的幅度,补偿MS算法近似处理所损失的性能.
1) NMS算法.通过除以一个数值来降低消息置信度的幅度,校验消息表示为
| $ L({r_{ji}}) \leftarrow \frac{1}{\alpha }L({r_{ji}}) $ | (6) |
其中α>1称为校正因子,此时改进算法称为Normalized MS算法.
2) OMS算法.通过减去一个数值来降低消息置信度的幅度,校验消息表示为
| $ L({r_{ji}}) \leftarrow {\rm{sgn}} [L({r_{ji}})]{\rm{max}}[|L({r_{ji}})| - \beta ,0] $ | (7) |
其中β称为偏移因子,此时改进算法称为Offset MS算法.校正因子和偏移因子的具体数值可以由密度进化渐近分析工具得到.
2.2 SCMS算法NMS和OMS算法是在校验节点消息处理上对MS高估的消息置信度做出一定的修正.而Savin等提出的SCMS算法是从变量节点消息的更新出发,修正消息传递过程中的置信度. SCMS算法的原理是:在变量节点消息处理过程中,根据变量节点消息的符号波动,有选择的擦除“不可信”的消息,这样可以加快收敛,在一定程度上恢复了MS算法损失的性能.下面为SCMS算法的节点消息在第l次迭代中的更新过程.
1) 变量节点消息更新
| $ {{L^{(l)}}({q_{ij}}) = {L^{(l - 1)}}({q_i}) - {L^{(l - 1)}}({r_{ji}})} $ | (8) |
| $ {e_{ij}^{(l)} = [ \backsim e_{ij}^{(l - 1)}][s_{ij}^{(l)} \oplus s_{ij}^{(l - 1)}]} $ | (9) |
| $ {{L^{(l)}}(q_{ij}^{\rm SC}) = [e_{ij}^{(l)} = 1]?0:{L^{(l)}}({q_{ij}})} $ | (10) |
2) 校验节点消息更新
| $ {L^{(l)}}({r_{ji}}) = \prod\limits_{{i^\prime } \in {R_j}\backslash i} {s_{{i^\prime }j}^{(l)}} \mathop {{\rm{min}}}\limits_{{i^\prime } \in {R_j}\backslash i} [|{L^{(l)}}(q_{{i^\prime }j}^{{\rm{SC}}})|] $ | (11) |
3) 判决量更新
| $ {L^{(l)}}({q_i}) = L({P_i}) + \sum\limits_{j \in {C_i}} {{L^{(l)}}} ({r_{ji}}) $ | (12) |
其中:符号“~”为取反;符号“⊕”为异或;符号“?:”为条件运算符;eij(l)用来指示本次迭代中L(l)(qij)被擦除的位置,避免相邻2次迭代重复擦除同一位置的消息;sij(l)为本次迭代中L(l)(qij)的符号;L(l)(qijSC)为根据擦除规则得到的新的变量节点消息.
SCMS算法沿用了MS算法在校验节点消息处的更新,而在变量节点消息的更新上,增加了一个可靠度的判断,如果变量节点消息的符号在连续2次迭代中发生改变,则视为不可靠消息,将其置为0,等待下一次更新.
在传统SCMS算法的基础上,针对如何更准确地判断出哪些变量节点的信息应该被擦除的问题,约束的SCMS(CSCMS,constrained SCMS)算法[12]中增加了一个判断条件:
| $ {L^{(l)}}(q_{ij}^{{\rm{CSC}}}) = {L^{(l)}}({q_{ij}})I[{L^{(l)}}({q_{ij}}),{L^{(l - 1)}}({q_{ij}})] $ | (13) |
若sij(l)=sij(l-1),或者|L(l-1)(qij)| < |L(l)(qij)|,I[L(l)(qij), L(l-1)(qij)]=1;否则为0. CSCMS算法与SCMS算法不同之处在于:当变量节点消息符号发生反转时,需要考虑|L(l)(qij)|的大小.
3 动态自纠正最小和算法SCMS算法阻止了不可靠信息的传递扩散,提高了算法的性能,但并没有明确说明如何判断消息的可靠性,并且在信噪比较高的情况下,SCMS算法的收敛性有所下降.基于SCMS算法,提出的DSCMS算法在判断变量节点消息的可靠性时,增加了阈值,动态调整擦除消息的范围区间,因此能够更好地适应不同的环境.另外,DSCMS算法在校验节点更新上采用NMS算法,从校验节点处理上保证译码算法的性能. DSCMS算法在变量节点消息更新过程中遵循的规则:如果变量节点消息向相反符号方向变动大于设定的阈值时,则判定为不可靠消息,并在更新中置为0,如图 1所示.
|
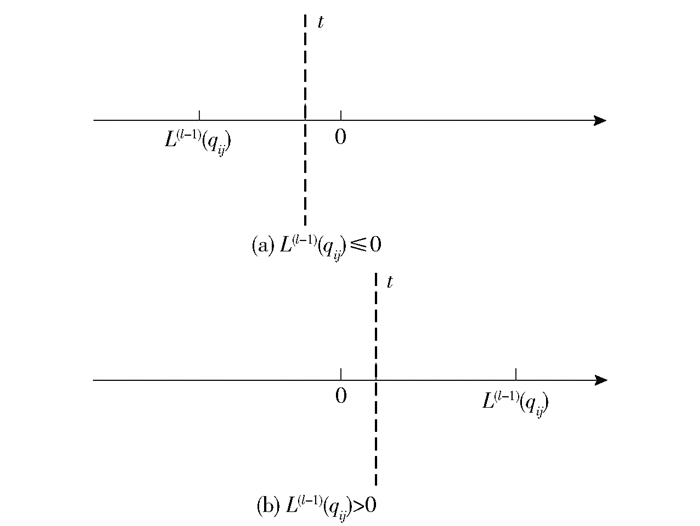
图 1 DSCMS算法可靠消息判定示意图 |
图 1中,L(l-1)(qij)为上一次迭代中的变量节点消息,t为所设的阈值.若L(l-1)(qij)为负值,那么当L(l)(qij)落在t的右侧,则会被擦除;若L(l-1)(qij)为正值,那么当L(l)(qij)落在t的左侧,则会被擦除.
阈值设定的考虑因素:如果t偏离L(l-1)(qij)较远,则只有较少数量的变量节点消息被修改,性能提升有限;另一方面,如果t偏离L(l-1)(qij)较近,则会有大量的变量节点消息被修改,扩大了不可靠消息的范围,引起译码性能下降.在这里,将阈值t定义为
| $ t = \theta {L^{(l - 1)}}({q_{ij}}) $ | (14) |
其中:θ为调节因子,其变化范围可取-0.5≤θ≤0.5,这样得到的t值不会偏离L(l-1)(qij)太近或太远.同时,t是一个关于L(l-1)(qij)的相对值,而L(l-1)(qij)在每次迭代中是变化的,t也会随着迭代更新而改变,因此判断可靠性的标准是自适应更新的.
DSCMS算法的消息更新过程描述如下:
1) 变量节点消息更新
| $ {{L^{(l)}}({q_{ij}}) = {L^{(l - 1)}}({q_i}) - {L^{(l - 1)}}({r_{ji}})} $ | (15) |
| $ {e_{ij}^{(l)} = [\backsim e_{ij}^{(l - 1)}]\{ s_{ij}^{(l - 1)}[{L^{(l)}}({q_{ij}}) - t] < 0\} } $ | (16) |
| $ {L^{(l)}}(q_{ij}^{{\rm{DSC}}}) = [e_{ij}^{(l)} = 1]?0:{L^{(l)}}({q_{ij}}) $ | (17) |
2) 校验节点消息更新
| $ {L^{(l)}}({r_{ji}}) = \prod\limits_{{i^\prime } \in {R_j}\backslash i} {s_{{i^\prime }j}^{(l)}} \mathop {{\rm{min}}}\limits_{{i^\prime } \in {R_j}\backslash i} [|{L^{(l)}}(q_{{i^\prime }j}^{{\rm{DSC}}})|]\frac{1}{\alpha } $ | (18) |
3) 判决量更新
| $ {L^{(l)}}({q_i}) = L({P_i}) + \sum\limits_{j \in {C_i}} {{L^{(l)}}} ({r_{ji}}) $ | (19) |
其中:α为NMS算法中的校正因子,L(l)(qijDSC)为根据新的擦除规则得到的变量节点更新消息.可以看出,当阈值t=0时,DSCMS算法即退变为传统的SCMS算法.
4 仿真结果与比较 4.1 DSCMS算法的性能仿真仿真中选择5G NR标准中的LDPC码,针对码率为1/2、码长为4 224 bit的情况[14],在Matlab平台中模拟加性高斯白噪声(AWGN,additive white Gaussian noise)信道,编码比特采用二进制相移键控(BPSK,binary phase shift keying)调制方式进行传输,基本仿真参数如表 1所示.
|
|
表 1 仿真参数 |
在文献[10, 12]中有其他算法的对比,在此只对SCMS、CSCMS、DSCMS算法进行仿真测试与比较,误比特率(BER, bit error ratio)、误块率(BLER, block error ratio)及平均迭代次数结果如图 2所示.

|
图 2 R=1/2时,SCMS、CSCMS、DSCMS算法的仿真曲线 |
从图 2可以看出,DSCMS算法在误码特性和收敛特性上都优于SCMS算法.而CSCMS算法在低信噪比(SNR,singal noise ratio)区域表现不佳,在SNR较高时,性能要优于SCMS算法.取图 2(c)中SCMS、CSCMS和DSCMS算法在不同信噪比下的平均迭代次数统计如表 2所示.
|
|
表 2 不同信噪比下各算法的平均迭代次数 |
从表 2可以看出,随着信道SNR的增大,LDPC译码的迭代次数在逐渐降低,DSCMS算法的收敛特性要优于SCMS算法,在高SNR区域与CSCMS算法相近.这是因为DSCMS与CSCMS算法都能够抑制不可靠消息的传递,加快了译码的收敛速度.而DSCMS算法对擦除消息的动态判断能够适应更广泛的信道环境.通过计算可得,在收敛特性上,DSCMS算法较SCMS算法最多能降低7.15%的迭代次数,平均降低5.95%.
4.2 译码算法的复杂度分析表 3示出了BP、MS、NMS、SCMS、CSCMS、DSCMS算法单次迭代的计算复杂度,其中N表示编码长度,K表示有效信息长度,W为校验矩阵的列重.
|
|
表 3 译码算法计算量比较 |
以MS算法为基础的改进算法,在BP算法的基础上,减少了大量的乘法和除法运算,在实现中会大大降低计算的复杂度.而DSCMS算法在变量节点消息处理中增加了少量的乘法和除法运算,在实现时,可将阈值调节因子定为1/2、1/4、1/8等,转化为简单的移位和加法运算得到相应的结果[15].总体上来说,DSCMS算法在增加少量计算复杂度的情况下,提高了译码算法的性能,降低了迭代次数.
5 结束语在SCMS算法的基础上提出了一种动态自纠正最小和算法,根据变量节点消息设置阈值,来判断消息是否可靠,并对不可靠消息进行擦除,等待下一次迭代更新.阈值设定为变量节点消息的相对值,会随着迭代的更新而改变,因此判断可靠性的标准是自适应更新的.仿真结果表明,在增加少量计算复杂度的情况下,DSCMS算法在一定SNR范围内都表现出了较好的性能,能够有效提升系统的误码特性与收敛特性,并且提高了系统的灵活性.
| [1] |
Jung Y, Jung Y, Lee S, et al. Low-complexity multi-way and reconfigurable cyclic shift network of QC-LDPC decoder for Wi-Fi/WIMAX applications[J]. IEEE Transactions on Consumer Electronics, 2013, 59(3): 467-475. DOI:10.1109/TCE.2013.6626226 |
| [2] |
Zhang Yishan, Zhang Chun, Yan Zhiyuan, et al. A high-through put multi-rate LDPC decoder for error correction of solid-state drives[C]//2015 IEEE Workshop on Signal Processing Systems(SiPS). Hangzhou: IEEE, 2015: 1-6.
|
| [3] |
Gallager R G. Low-density parity-check code[J]. IRE Transactions on Information Theory, 1962, 8(1): 21-28. DOI:10.1109/TIT.1962.1057683 |
| [4] |
Richardson T, Kudekar S. Design of low-density parity check codes for 5G new radio[J]. IEEE Communications Magazine, 2018, 56(3): 28-34. DOI:10.1109/MCOM.2018.1700839 |
| [5] |
张睿, 朱敏, 张冀, 等. 面向5G的递增冗余HARQ传输方案研究[J]. 北京邮电大学学报, 2018, 41(5): 92-97. Zhang Rui, Zhu Min, Zhang Ji, et al. Study on 5G incremental redundancy HARQ transmission strategy[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(5): 92-97. |
| [6] |
MacKay D J C, Neal R M. Near Shannon limit performance of low density parity check codes[J]. Electronics Letters, 1996, 32(18): 1645-1646. DOI:10.1049/el:19961141 |
| [7] |
Fossorier M P C, Mihaljevic M, Imai H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation[J]. IEEE Transactions on Communications, 1999, 47(5): 673-680. DOI:10.1109/26.768759 |
| [8] |
Chen J, Fossorier M P C. Density evolution for two improved BP-based decoding algorithms of LDPC codes[J]. IEEE Communications Letters, 2002, 6(5): 208-210. DOI:10.1109/4234.1001666 |
| [9] |
Chen J, Fossorier M P C. Near optimum universal belief propagation based decoding of low-density parity check codes[J]. IEEE Transactions on Communications, 2002, 50(3): 406-414. DOI:10.1109/26.990903 |
| [10] |
Savin V. Self-corrected min-sum decoding of LDPC codes[C]//2008 IEEE International Symposium on Information Theory. Toronto: IEEE, 2008: 146-150.
|
| [11] |
Boncalo O, Amaricai A, Mihancea P F, et al. Memory trade-offs in layered self-corrected min-sum LDPC decoders[J]. Analog Integrated Circuits and Signal Processing, 2016, 87(2): 169-180. DOI:10.1007/s10470-015-0639-3 |
| [12] |
韩少聪, 高飞飞, 李云洲, 等. 一种改进的自纠正最小和LDPC码的译码算法[J]. 电信科学, 2013(6): 95-99. Han Shaocong, Gao Feifei, Li Yuzhou, et al. An improved self-correct min-sum decoding algorithm for low-density parity-check code[J]. Telecommunications Science, 2013(6): 95-99. |
| [13] |
袁东风, 张海刚, 马丕明, 等. LDPC码理论与应用[M]. 北京: 人民邮电出版社, 2008: 72-78.
|
| [14] |
3GPP TSG RAN WG1. Multiplexing and channel coding(Release 15): 3GPP TS 38.212 V15.1.1-2018[S]. Valbonne: 3GPP, 2018: 28.
|
| [15] |
Xiang Bo, Shen Rui, Pan An, et al. An area-efficient and low-power multirate decoder for quasi-cyclic low-density parity-check codes[J]. IEEE Transactions on Very Large Scale Integration(VLSI)Systems, 2009, 18(10): 1447-1460. |



