为了对长周期定点轨迹数据进行行程识别,提出了一种基于动态阈值的定点轨迹数据行程识别方法.首先,采用聚类方法确定与阈值相关的时空多粒度参数;其次,根据参数对历史记录进行统计,计算参数对应的阈值;利用时空相关参数获取对应阈值,对轨迹进行分段,进而实现行程识别.基于真实的城市交通卡口数据的实验结果表明,使用时空相关的动态阈值方法对定点轨迹数据进行行程识别在准确率和覆盖率上都要优于传统基于固定和单一阈值的方法.
To satisfy the requirements of long-periodic fixed-point trajectory travel recognition, a dynamic threshold travel recognition method for fixed point trajectory data is proposed. At first, use hierarchical clustering to determine the spatial-temporal multiple granularity parameters which relate to the threshold. Then count historical records according to parameters to calculate the threshold corresponding to each parameter. Last, execute trajectory segmentation process with spatial-temporal threshold to get the precise travel recognition result. Experiment based on fixed-point trajectory data from real world city shows that using spatial-temporal dynamic threshold method to recognize travel in fixed point trajectory data is superior to the traditional stable and single threshold method on accuracy and coverage.
轨迹数据是指通过对移动对象运动过程的采样所形成的具有时空特征的数据信息[1].随着采集技术的不断发展和采集设备的大量部署,产生了越来越多的移动对象轨迹数据.这些轨迹数据可以用来交通规划,城市规划,兴趣推荐等,具有广泛的意义和重要的价值.
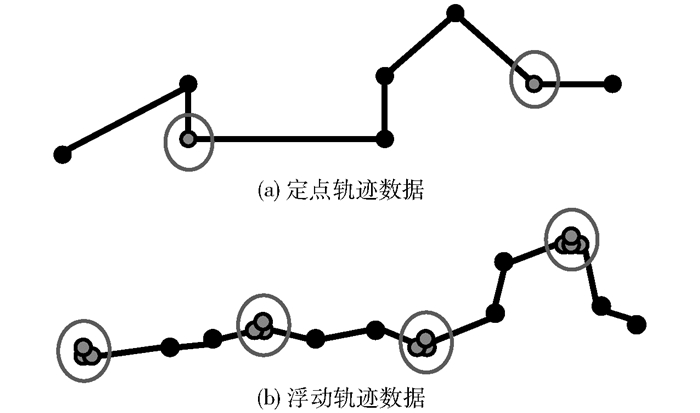
根据轨迹数据采集方式的不同,可把轨迹数据分为两类:基于固定位置设备采集的定点轨迹数据和基于移动设备采集的浮动轨迹数据,2种数据如图 1所示.定点采集意味着数据监测点是固定不变的,当目标物体出现时,记录目标出现的时间即可.这种记录方式数据冗余度较低,但是数据缺失度较高,常见的定点的采集方式有:交通卡口/识别点数据,基于通信基站的手机信令数据,基于车牌/卡的射频识别(RFID,radio frequency identification)数据等等.而浮动点采集是指采集设备伴随目标物体运动,周期性的记录物体的时空信息.这种方式数据冗余度较高,但是缺失度较低,常见的方式有:车载全球定位系统(GPS,global positioning system)定位器,手机位置服务,船舶自动识别系统等.定点轨迹数据,图 1(a)所示,具有轨迹点相对稀疏,轨迹点间时间间隔不等,不存在显式的停留语义等特征.而浮动轨迹数据,图 1(b)所示,数轨迹点密集,存在一定程度的冗余,存在明显的停留特征点.
|
图 1 定点轨迹数据与浮动轨迹数据 |
一般来说,以上2种采集方式获得的数据,按照移动对象整理后得到的往往是长周期的连续轨迹,即可能为对象多次出行累积的数据.而为了方便轨迹数据的存储、查询以及出行分析,需要对移动对象的每次出行进行轨迹数据区分,即进行行程识别.行程识别的含义是对长时段轨迹(例如以天或月为单位)按照每次出行的语义进行合理切分与标注,切分后的子轨迹段代表一次出行的记录[2].因此,行程识别问题可以看作是一类特定的轨迹分段问题.轨迹分段是属于数据概要的一个分支.数据概要是指对数据进行压缩使之成为信息性表示,换句话说,它是保留有用信息,清除冗余,并且保留的信息具有代表性,是对源数据的一种抽象[3].轨迹分段可以定义为:将轨迹分划分成尽可能少的轨迹段,并且在某种意义上,不同轨迹段之间,它们内部的运动特征是不同的[4].高效而准确的轨迹分段,会为轨迹数据的挖掘工作提供了质量保证.同时轨迹分段作为轨迹金字塔基层——轨迹预处理中的一个基本问题,其对后续的轨迹仓库的构建、轨迹查询和时空语义分析有至关重要的意义.
现有主流的轨迹分段方式包括基于时间阈值、几何拓扑和轨迹语义这3种基本策略.与时间阈值策略相关的工作有:张治华[5]提出了两类轨迹段的概念,使用单一速度阈值对轨迹段进行分类,进而对轨迹段进行合并,实现对轨迹的分段. Du等[6]提出使用单一时间阈值对轨迹进行停留点检测从而划分轨迹段.张健钦等[7]提出了利用速度阈值划分,时间阈值与距离阈值进行筛选的多层判别的停留点识别方法,解决了数据的漂移和抖动问题.与几何拓扑策略相关的工作有:Du等[6]结合几何关系分析目标是否脱离路网. Palma[8]对停留和运动轨迹算法(SMoT,stops and moves of trajectories)[9]进行了改进,提出了一种基于密度对噪声鲁棒的空间聚类(DBSCAN,density-based spatial clustering of applications with noise)的停留点识别算法,对于离散度较高的轨迹,可以识别更多未知的停留点.文献[10]提出了基于停留和运动轨迹的时空聚类算法(STC-SMoT,spatio temporal clustering-based stops and moves of trajectories),用于在数据存在缺失和噪声情况下进行轨迹分段. Damiani和Hachem等[4, 11]介绍了一种基于聚类的分段方法,提出了算法SeqScan.该算法可以最大化利用基于密度的规则,以加快基于空间密度规则的轨迹分段计算.与轨迹语义策略相关的工作有:侯颖超等[12]提出了一种速度变量的停留点提取方法,该方法首先进行时间和速度聚类获得备选停留点,再通过速度阈值过滤,得到实际停留点,增强了停留点识别的准确性. Soares Junior Amilcar等[13-14]提出了一种非监督的轨迹分段算法,该算法能够自适应界标,使用基于MDL(minimum description length)原则的评价函数来实现分段结果中的高同质性.该方法无需预先为任何类型的轨迹特征确定标准就可以对样本轨迹进行分割[15].王京[16]提出了一种基于皮尔逊相关系数的轨迹停留点识别算法,缩小了停留点的识别范围,提高了停留点算法的识别效率. Zheng等[17]基于GPS数据,挖掘其中的兴趣点,再通过对历史数据学习得到停留点,用停留点实现对轨迹的分段.综上可以看出,对轨迹进行停留点检测,利用停留点对轨迹进行分段是目前比较主流的方法之一.
然而,以上研究都是对浮动轨迹数据进行轨迹分段,对于定点轨迹数据来说,由于采集方式的局限性,其轨迹不存在显式的停留语义,故停留点检测的方式将不再适用. Du等[6]中还提出了一种针对轨迹点缺失情况下的行程划分方法,该文利用缺失前的速度对缺失时间进行预测,与实际缺失时间进行对比,进而对轨迹进行分段.在一定程度上,定点轨迹与缺失情况下的浮动轨迹有相似之处:连续记录点之间的时间间隔较长,并且缺失运动状态发生变化的记录点.因此,尝试使用速度阈值的方式对定点轨迹进行分段.张治华[5]提出了一种阈值划分的方法,但是该方法没有考虑到阈值的时空差异,不能直接用于定点轨迹的划分.
该针对上述方法的局限性,结合定点轨迹数据的时空特性,提出一种基于动态阈值的定点轨迹数据行程识别方法.该方法细化了轨迹分段工作的针对性,当处理不同特征的轨迹数据时,通用的方法不能达到预期的效果,需要对结合数据特征本身,制定个性化的分段方法.方法根据某路段平均消耗时间作为阈值来判断目标物体在路径上是否存在停留行为,进而进行轨迹分段,对于定点数据等离散度较高的轨迹数据分段有较好的准确率提升.方法的创新点在于对阈值计算时,结合轨迹数据的时空相关性,设置多粒度的时空参数对阈值进行动态调整,而不是采用传统的固定阈值方法.基于深圳市的城市交通卡口车牌识别数据对方法的有效性进行验证.
1 问题定义 1.1 相关定义定义1(监测点) 监测点d(x, y)是采集设备的部署点,其具有空间属性,x代表经度,y代表纬度.所有监测点d(x, y)构成的集合称为监测点集D,可以表示为{D|di(xi, yi)∈D, i=0, 1, 2, …, n}.
定义2(时空点) 形如p=(x, y, t)的点称作时空点,其中x代表经度,y代表纬度,t描述时空点的时间属性,其表示移动对象在t时刻的空间位置.定点采集设备获得的时空点可以表示为p=(d, t),其中d=(x, y),其空间属性构成的空间点(x, y)均属于监测点集合D.
定义3(轨迹) 轨迹T是由移动对象产生的一组有序的时空点组成的集合,T={p0, p1, …, pn},其中pi=(xi, yi, ti), i∈{1, 2, …, n},当i < j时,ti < tj.对于定点轨迹数据,pi=(di, ti), i∈{1, 2, …, n},当i < j时,ti < tj.
定义4(关键点) 对于轨迹上2个连续的时空点pi, pi+1∈T,vthresh为速率阈值,若
定义5(单次出行轨迹) 根据定义3,将缺失关键点的轨迹分为两段子轨迹:T1={p0, p1,…, pi}和T2={pi+1, …, pn},如果对于某一段子轨迹不存在关键点pkey,称这段子轨迹为单次出行轨迹Ttravel.单次出行轨迹用来描述目标一次出行的运动情况.
1.2 问题定义给定移动对象的一条长周期的定点轨迹数据T={p0, p1, …, pn},其中tn-t0>24 h,识别出该轨迹中存在的所有单次出行轨迹Ttravel.
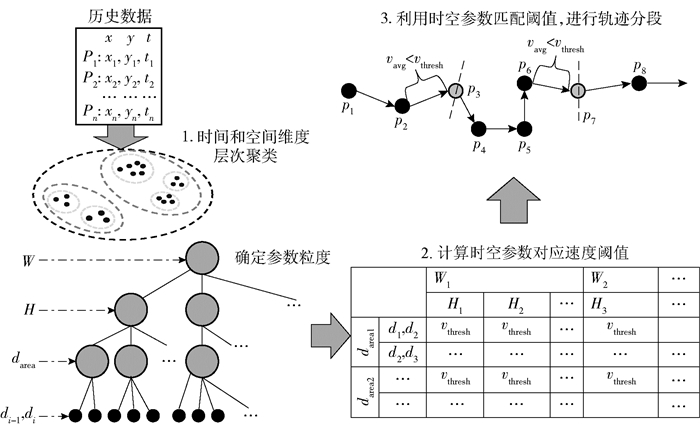
2 基于动态阈值的定点轨迹数据行程识别方法该方法在固定阈值的轨迹分段方法上进行了改进,针对不同时空情况,有不同的判断阈值. 图 2所示为该方法的主要流程,分为3个主要步骤:1)对历史数据进行时空相关分析,确定参数选取的维度,再利用层次聚类的方法,对粒度进行划分,获取时空相关的阈值参数;2)根据时空参数对历史数据进行分组,计算每组对应速度阈值;3)将测试数据的时空参数与历史数据的参数进行匹配,获取速度阈值,作为判断轨迹分段的条件,以此实现轨迹分段,达到行程识别的目的.
|
图 2 动态阈值的定点轨迹数据行程识别方法流程 |
由于轨迹数据是一类特殊的时空数据,其数据都具有时空特性.对轨迹点之间的速度进行了时空相关性的分析.
图 3显示了同一时间下,通过不同监测点的平均速度,图中点越大表示通过该监测点的速度越大.

|
图 3 某日15时车辆通过部分监测点的平均速度示意图 |
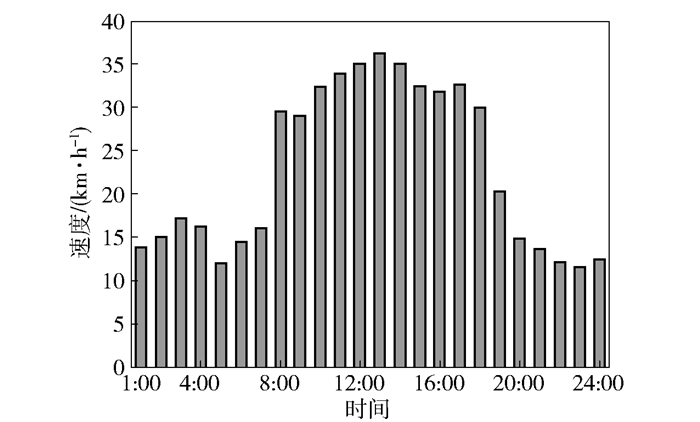
图 4显示了同一个检测点,不同时间段的平均速度.可以看出,空间和时间对于速度都有不同的影响,所以在设置阈值的时候参考时间空间2个属性.
|
图 4 某日车辆通过某路口监测点的平均速度统计 |
确定阈值的参数维度之后,还需要考虑参数的粒度.细粒度参数带来的是高准确率,但同时会出现大量无法根据参数选取阈值的情况.粗粒度参数会为大量的轨迹点提供判断,但准确率会降低.根据数据的时空属性,规定了原子粒度,即不可以再细化分割.基于原子粒度,使用聚类方法自底向上逐渐得到粗粒度参数.
1) 层次聚类获取时间阈值参数粒度
在对时间日期聚类时,要满足以下2个要求:在聚类时需要设置最终结果簇数;所选方法尽可能地减少度量标准对于聚类结果的影响.由于层次聚类不需像DBSCAN等算法要调节聚类参数,产生的结果要比K-means等算法相对稳定[18],并且满足上文提到的2种要求,故选择使用层次聚类的方法来生成粗粒度参数.算法1为参数粒度的层次聚类算法.
算法1 层次聚类算法
输入: G:样本集合; N:聚类数目;
输出:聚类结果
1将G以原子粒度为单位统计车流量;
2将每个原子粒度都当做一个独立的类簇;
3 repeat
4 计算两两类簇之间的车流量之差Edis;
5 找到Edis最小的2个类簇c1和c2;
6合并类簇c1和c2为一个类簇;
7 until达到聚类的数目N
表 1所示为时间参数的粒度设置,粒度等级数字越大,表示粒度越粗,0表示原子粒度.采用的时间原子粒度为以7 d为周期的相同小时.
|
|
表 1 时间参数粒度 |
时间段H由小时聚类获得,工作日W由星期聚类获得.统计每天的车流量和每小时的车流量,用车流量的差值表示2个数据点的距离.
2) 密度聚类获取空间阈值参数粒度
对于空间参数,采用基于密度的聚类方式.该聚类方法的依据是各个监测点的可连接性,对于空间距离较近的监测点之间的移动物体,其运行状态具有相似性.
设置了3个空间参数粒度等级.由于轨迹的监测点是固定的,2个相邻的监测点dm、dn可以构成一个空间参数,表 2所示为空间参数粒度.区域darea由监测点d聚类获得.
|
|
表 2 空间参数粒度 |
根据阈值的选取参数,对训练集的数据进行分组,符合时空参数条件的数据为一组,其中时空参数包括时间参数W、H和空间参数dm、dn.对于给定的一组时空参数,会对应一组含有n行数据的数据组,每行应该包含2个轨迹点.第i行可以表示为pi=(xi, yi, ti), pj=(xj, yj, tj),其中xm=xi, xn=xj, ym=yi, yn=yj,并且ti.W⊂W, ti.H⊂H.
计算第i行两点间的平均速度为
| $ v_{i}=\frac{\sqrt{\left(y_{i}-y_{j}\right)^{2}+\left(x_{i}-x_{j}\right)^{2}}}{t_{j}-t_{i}} $ |
n行记录对应了n个平均速度,求v的期望为
| $ E(v)=\frac{1}{n} \sum\limits_{1}^{n} v_{i} $ |
以此记作该参数下的速度阈值,即
| $ v_{w-H-d_{m}-d_{n}}=E(v) $ |
阈值的选取参数粒度不同,对应的速度阈值也就不同,所以对于每一种粒度的参数,都要进行分组计算其速度阈值.
2.4 长周期轨迹数据分段如图 5所示,根据定义3,对长周期的轨迹T={p0, p1, …, pn}进行遍历,计算每2个时空点之间的平均速度vavg,而每2个空间点pi-1, pi都会根据时空参数匹配一个速度阈值vthresh,通过平均速度vavg与速度阈值vthresh的比较,寻找轨迹中所有的关键点pkey,最后以关键点pkey对轨迹进行分段,提取Ttravel,输出行程轨迹段.算法2为动态阈值轨迹分段算法.

|
图 5 长周期轨迹数据分段 |
算法2 轨迹分段算法
输入: T:移动目标的一段长周期运行轨迹; vthresh:速度阈值;
输出: Ttravel:移动目标的出行轨迹集合;
1 initial i=1;
2 j=1;
3 count=0;
4 Ttravel [count].p[0]=T.p[0];
5 while T.p[i]!=null do
6 varg=Velocity(T.p[i-1], T.p[i]);
7 vthresh=GetThresh(T.p[i-1], T.p[i]);
8 if varg < vthresh then
9 j=0;
10 count++;
11 Ttravel [count].p[j]=T.p[i];
12 else
13 Ttravel [count].p[j]=T.p[i];
14 end if
15 j++;
16 i++;
17 end while
18 return Ttravel
该算法最为关键的部分是阈值的获取.阈值获取合适,判断的关键点就越准确,对划分结果就越接近实际情况.阈值获取策略根据粒度等级来决定,粒度值越小,就表示范围越精确,在进行判断的时候以此为标准.
3 实验评价 3.1 实验环境实验环境基于3台搭建Hadoop环境的Linux虚拟机,Hadoop集群由1个Master节点和2个Slave节点构成,其配置均为主频2.0 GHz的双核CPU、4 GB内存.
3.2 实验数据使用来源于深圳市的车牌识别数据.该数据中记录了1 760 776辆车13 d的出行记录.为了验证提出的方法,将数据集以时间为界分为2段,前7天为训练集,生成阈值数据集,后6天为测试集,用作验证方法的正确性. 表 3列出了实验数据的统计信息.
|
|
表 3 实验数据的统计信息 |
为了方便评价,仅挑选了测试集中,轨迹点记录数量超过100的车辆进行分割.
3.3 评价指标实验评价主要考虑识别结果的准确性和覆盖性.
定义6(查准率和查全率) R表示实际关键点的集合,R′表示算法标注的关键点集合,那么查准率可以表示为
| $ P_{\mathrm{acc}}=\frac{R \cap R^{\prime}}{R^{\prime}} \times 100 \% $ |
查全率可以表示为
| $ P_{\mathrm{rec}}=\frac{R \cap R^{\prime}}{R} \times 100 \% $ |
1) 层次聚类时间阈值参数
在实验中发现,如果匹配的时间和空间参数粒度过细,会出现大量无法判断的轨迹点.为此,考虑降低参数粒度.
根据2.2节中时间阈值参数粒度的划分结果,以记录数量为依据,对训练集和测试集进行了时间维度的层次聚类.
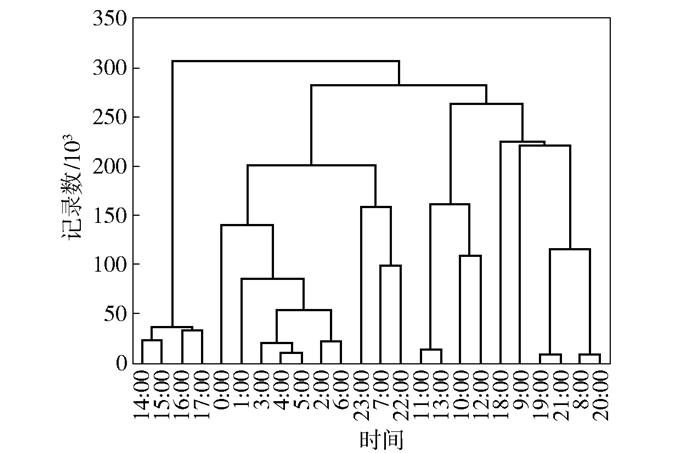
首先是对小时进行聚类,统计每个小时的记录数,将记录数作为距离进行层次聚类.层次聚类有很多种方法,实验使用了“单连接”、“全连接”、“均连接”3种方法进行聚类.聚类的中间结果会出现差异,但最后得到的结果均相同. 图 6、图 7所示分别为训练集和测试集的单连接聚类结果.

|
图 6 训练集单连接小时聚类结果 |
|
图 7 测试集单连接小时聚类结果 |
可以看出,由于记录数不同,不同簇之间的差值可能与训练集相差较大,但是聚类结果与训练集相差无异.最终将聚类簇的数量限制为5个,可以得到如表 4所示的聚类结果.
|
|
表 4 小时层次聚类结果 |
为了方便匹配阈值,对聚类的结果进行了调整,得到如表 5所示的5个时间段.
|
|
表 5 调整后的小时聚类结果 |
对日期的聚类结果如图 8和图 9所示.为了与工作日和非工作日的分类方法作对比,将日期的结果簇数量设置为2.

|
图 8 训练集单连接日期聚类结果 |

|
图 9 测试集单连接日期聚类结果 |
从图 8可以看出,与历史的工作和休假信息相比,通过聚类得到的结果与之偏差较大. 图 9说明了测试集和预测集的聚类结果相似,但与历史的工作和休假趋势不同.最终得到表 6的聚类结果.
|
|
表 6 日期聚类结果 |
将小时和日期的聚类结果整合,最终通过聚类得到的时间阈值划分如表 7所示.
|
|
表 7 层次聚类分段 |
利用聚类得到的时间阈值逐渐调整条件范围,进行4个流程的补充判断.每个阶段所补充判断的记录数和丢失率如表 8所示.
|
|
表 8 基于层次聚类分段的补充判断结果 |
阈值条件的调整方法扩大了可判断的记录范围,能有效地减少无法判断的情况.
2) 密度聚类空间阈值参数
基于密度的聚类方式需要确定2个参数:样本邻域阈值和邻域内的样本个数.
由于监测点附近的监测点可能存在相同的运动状态,在进行聚类时,主要考虑距离对于聚类结果的影响,因此邻域内的样本个数设置了最小值2,用控制变量法选取了最优的样本邻域阈值.
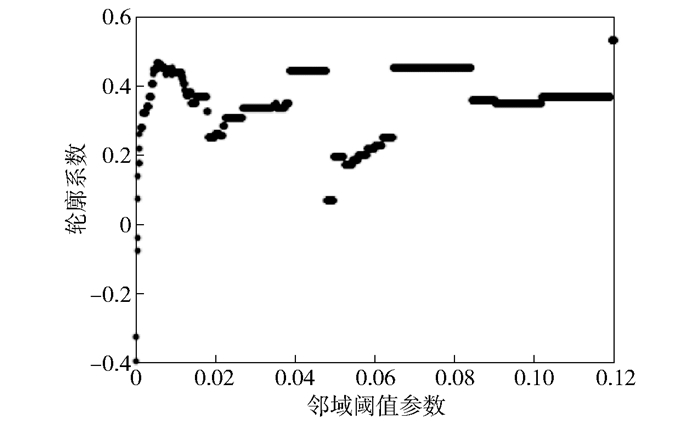
图 10所示为样本邻域阈值与轮廓系数的关系.
|
图 10 样本邻域阈值与轮廓系数的关系 |
轮廓系数是描述聚类效果好坏的一种评价方式,轮廓系数越趋近于1,代表内聚度和分离度都相对较优.可以看出,邻域阈值在0.009 1、0.045、0.066和0.120时获得的轮廓系数较高.
表 9展示了4个轮廓系数最高的邻域阈值的聚类簇数和噪点数.
|
|
表 9 不同邻域阈值的聚类结果 |
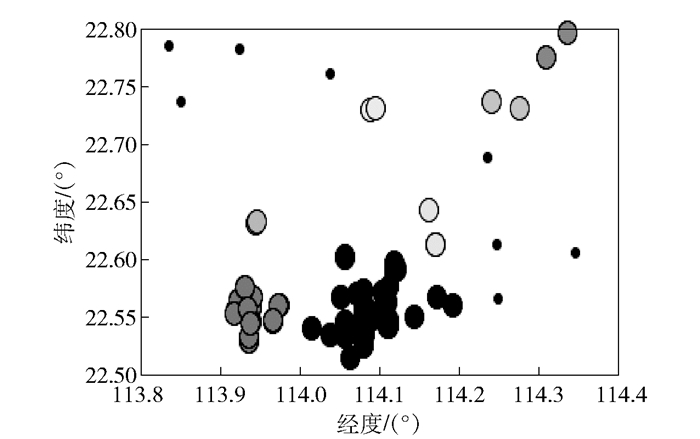
为了使簇数尽可能多,噪点数尽可能少,选择0.045作为邻域阈值参数,最终聚类结果如图 11所示.
|
图 11 监测点基于密度聚类结果 |
3) 轨迹分段方法准确性
在准确率和覆盖率评价时挑选了轨迹点数大于100的记录进行实际分段验证.该记录时间跨度为6天,总共包含16 808条轨迹,3 488 760个轨迹点,平均每条轨迹含有207个轨迹点,最高轨迹点数达到708,保证了所有轨迹都是长周期轨迹.
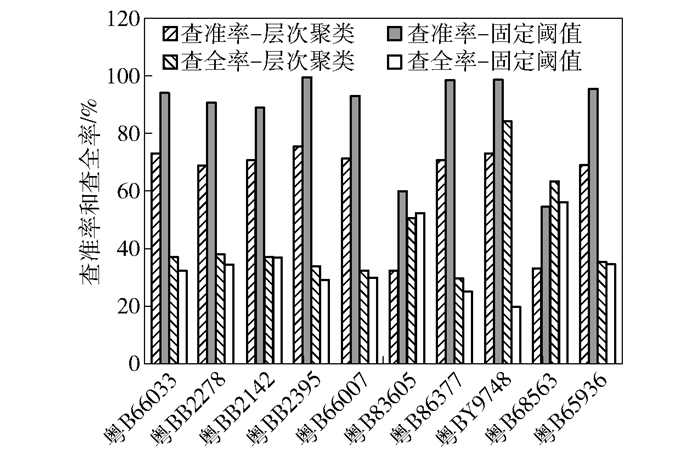
图 12显示了动态阈值与固定阈值方法对轨迹点最多的10条轨迹分段结果.
|
图 12 动态阈值和固定阈值方法对轨迹点数最多的10条轨迹的分段结果对比 |
固定阈值的设置参考了Du等[6]在其行程识别工作中的取值0.51 m/s.可以看出,有80%的情况前者查全率和查准率都要优于后者40%~50%左右.对于有2条轨迹采用固定阈值反而取得了更好的查准率,有1条轨迹采用固定阈值取得了更好的查全率的情况,通过查阅轨迹数据发现,该3条轨迹中出现无法判断的点的情况较多,无法通过时空参数获取对应速度阈值,部分轨迹点无法通过动态阈值方法进行判断,而固定阈值方法却不受此限制,故出现了反常情况.
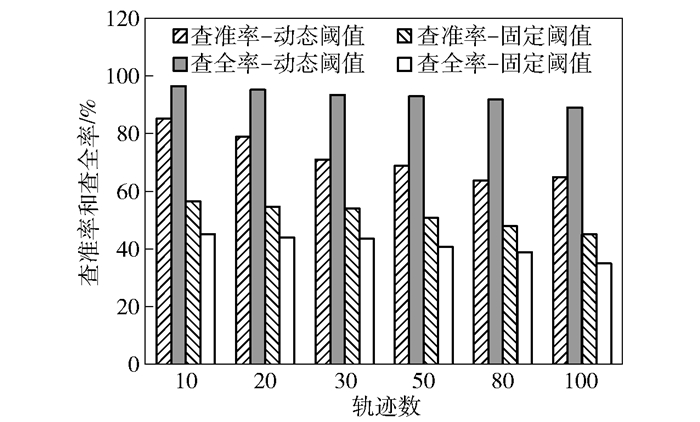
图 13显示了轨迹条数与评价指标的关系,从图中可以看出,随着轨迹条数的增加,查准率和查全率呈下降趋势.但是,动态阈值的分段结果要优于固定阈值的方法.
|
图 13 轨迹数与评价指标的关系 |
表 10显示了聚类动态阈值与固定阈值的轨迹点总体的分段结果.在查准率上,动态阈值的方法要比固定阈值的方法高出20%,在查全率上要高出51%.综合看来,提出的方法在对于定点轨迹数据行程识别比较有效.
|
|
表 10 聚类动态阈值与固定阈值分段部分结果 |
针对定点轨迹数据,提出了一种动态阈值的轨迹行程识别方法.首先将行程识别问题转化为轨迹分段问题.考虑到定点轨迹数据的离散度较高的特性,采用了速度阈值对轨迹进行分段.由于车辆的行驶速度会受到时空化影响,在轨迹分段时速度阈值也应当考虑时空因素.实验结果证明,使用时空相关的速度阈值对定点轨迹数据进行行程识别在准确率和覆盖率上都要优于固定速度阈值.提出的行程识别方法还待完善,比如时空化的阈值也不是固定不变的,需要一种时空阈值的更新策略,使得识别结果更为精确;由于车辆实际的行程起始点并不总是与监测点重合,为了得到行程更加精确的起始点,需要对空间进行语义标注,寻找监测点之外的行程起始点.
| [1] |
高强, 张凤荔, 王瑞锦, 等. 轨迹大数据:数据处理关键技术研究综述[J]. 软件学报, 2017, 28(4): 959-992. Gao Qiang, Zhang Fengli, Wang Ruijin, et al. Trajectory big data:a review of key technologies in data processing[J]. Journal of Software, 2017, 28(4): 959-992. |
| [2] |
许佳捷, 郑凯, 池明旻, 等. 轨迹大数据:数据、应用与技术现状[J]. 通信学报, 2015, 36(12): 97-105. Xu Jiajie, Zheng Kai, Chi Mingmin, et al. Trajectory big data:data, applications and techniques[J]. Journal on Communications, 2015, 36(12): 97-105. |
| [3] |
Damiani M L, Hachem F. Segmentation techniques for the summarization of individual mobility data[J]. Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery, 2017, 7(6): e1214. |
| [4] |
Damiani M L, Hachem F, Issa H, et al. Cluster-based trajectory segmentation with local noise[J]. Data Mining and Knowledge Discovery, 2018, 32: 1017-1055. DOI:10.1007/s10618-018-0561-2 |
| [5] |
张治华.基于GPS轨迹的出行信息提取研究[D].上海: 华东师范大学, 2010.
|
| [6] |
Du J, Aultman-Hall L. Increasing the accuracy of trip rate information from passive multi-day GPS travel datasets:automatic trip end identification issues[J]. Transportation Re-search, Part A(Policy and Practice), 2007, 41(3): 220-232. DOI:10.1016/j.tra.2006.05.001 |
| [7] |
张健钦, 仇培元, 徐志洁, 等. 一种基于手机定位数据的出行行程识别方法[J]. 武汉理工大学学报, 2013(5): 934-938. Zhang Jianqin, Qiu Peiyuan, Xu Zhijie, et al. A method to identify trip based on the mobile phone positioning data[J]. Journal of Wuhan University of Technology, 2013(5): 934-938. |
| [8] |
Palma A T, Bogorny V, Kuijpers B, et al. A clustering-based approach for discovering interesting places in trajectories[C]//ACM Symposium on Applied Computing. Fortaleza: ACM, 2008: 863-868.
|
| [9] |
Alvares L O, Bogorny V, Kuijpers B, et al. A model for enriching trajectories with semantic geographical information[J]. Proceedings of the 15th Annual ACM International Symposium on Advances in Geographic Information Systems, 2007, 22: 1-8. |
| [10] |
Hwang S, Vandemark C, Dhatt N, et al. Segmenting human trajectory data by movement states while addressing signal loss and signal noise[J]. International Journal of Geographical Information Science, 2018(7): 1391-1412. |
| [11] |
Hachem F, Damiani M L. Periodic stops discovery through density-based trajectory segmentation[C]//SIGSPATIAL' 18. New York: ACM Press, 2018: 584-587.
|
| [12] |
侯颖超, 王盼成, 刘兴权, 等. 基于速度的空间轨迹停留点提取算法[J]. 地理与地理信息科学, 2016(6): 63-68. Hou Yingchao, Wang Pancheng, Liu Xingquan, et al. Algorithm study for stay points recognition of spatial trajectory based on velocity[J]. Geography and Geo-Information Science, 2016(6): 63-68. |
| [13] |
Soares Junior Amilcar, Moreno Neiva Moreno, Times Valéria Cesário, et al. GRASP-UTS:an algorithm for unsupervised trajectory segmentation[J]. International Journal of Geographical Information Science, 2015, 29(1): 46-68. |
| [14] |
Soares Junior Amilcar, Times Valéria Cesário, Chiara Renso, et al. A semi-supervised approach for the semantic segmentation of trajectories[C]//Proceedings of the 19th IEEE International Conference on Mobile Data Management. New York: IEEE, 2018(1): 145-154.
|
| [15] |
Wu Ruizhi, Luo Guangchun, Shao Junming, et al. Location prediction on trajectory data:a review[J]. Big Data Mining and Analytics, 2018, 1(2): 108-127. DOI:10.26599/BDMA.2018.9020010 |
| [16] |
王京.基于相关系数的轨迹停留点识别算法[D].武汉: 华中师范大学, 2016.
|
| [17] |
Zheng Yu, Zhang Lizhu, Xie Xing, et al. Mining interesting locations and travel sequences from GPS trajectories[C]//Proceedings of the 18th International Conference on World Wide Web. New York: ACM Press, 2009: 791-800.
|
| [18] |
Bao Jie, He Tianfu, Ruan Sijia, et al. Planning bike lanes based on sharing-bikes' trajectories[C]//Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM Press, 2017: 1377-1386.
|



