由于无线信道存在衰落,射频能量收集(EH)器可将收集到的电磁波能量转化为用于无线通信的电源,其功率具有动态随机特性.为此,研究了Nakagami-m信道衰落下的多时隙"收集-存储-使用"能量收集方案的有效吞吐量以及"收集-使用"能量收集方案的二进制相干和非相干解调平均误比特率性能指标,推导出了精确的理论闭合公式.仿真结果表明,在Nakagami-m信道衰落的无线通信环境下,采用"收集-存储-使用"能量收集方案的无线通信存在最佳时隙数,以实现最大有效的吞吐量,而采用"收集-使用"的能量收集方案时,无线通信会使用少量时隙来平衡误码率和通信迟延.
Due to the fading of the channel, the energy harvester converts the harvested electromagnetic wave energy into a power source for transmitting wireless signals again, and its power has random dynamic characteristics. Aiming at the wireless communication environment with Nakagami-m channel fading, linear radio frequency energy harvesters combining with multi-slot "harvest-storage-use" and "harvest-use" schemes to realize EH are proposed. The effective throughput of the "harvest-storage-use" EH scheme and the average bit error rate of binary digital coherent and incoherent demodulation of the "harvest-use" EH scheme are studied and analyzed. The simulation results show that the wireless communication adopting the "harvest-storage-use" strategy has the optimal number of time slots to achieve the best effective throughput, while the wireless communication adopting the "harvest-use" EH scheme should use a small number of time slots to balance the bit error rate and communication delay.
近年来,一种被称为能量收集(EH,energy harvesting)的技术被研发出来,实现便携式无线通信设备从周围环境或专用电源以非接触的方式收集能量,为自身通信提供所需的持续电力[1].能量可以从周围环境或特定能量源进行收集,例如太阳、风或电磁波.因为电磁波广泛存在并具有易于收集的特点,电磁波的射频能量收集有望成为能量受限无线通信极具前景的解决方案[2-3].
射频EH技术可以分为时间切换、功率分配和理想技术[4].在时间切换EH中,传输时隙的特定部分用于从接收到的射频信号中收集能量,其余部分用于后续信息处理.如基站向远端设备广播能量,远端设备进行能量收集,然后远端设备使用收集到的功率发送它们的数据[5].这种方案也适用于通过EH设备收集周围环境中射频功率,如电视、广播或蜂窝信号[6-7].在功率分配EH中,EH设备将输入信号能量分为2部分:一部分转换为能量; 另一部分用于处理信息,实现射频能量传输和信息传输同时进行,实现利用相同的射频信号进行无线功率和信息传输[8].理想技术则希望远端设备具有同时收集能量并处理信息的能力,每个信息都包含接收信号的总能量,实现较为困难.已有多篇文献研究了以上EH收集技术用于各种形式的无线通信,如中继协作网络、5G、认知无线电和传感器网络等,实现绿色通信[9-13].
对于采用时间切换的射频EH技术,可以分为“收集-存储-使用”和“收集-使用”方案. “收集-存储-使用”方案需要大容量和低泄露的可充电电池,能量先被存储,在累积了足够的能量之后,才会通过使用固定的传输功率来执行数据传输,提供固定速率的服务[14]. “收集-使用”方案是能量在收集后立即使用,该方案的优点是低容量的廉价超级电容器可用于节省存储成本以及简化能量管理策略,缺点是由于EH设备每次传输耗尽收集的能量,传输功率具有随机特性[15].这是因为无线信道具有衰落随机特性,远端的EH设备收获的能量则具有了动态特性,用于再次信息传输的能量也变得随机[16].信道衰落的随机特性如瑞利、Nakagami-m、莱斯信道衰落的严重程度以及莱斯信道衰落中的视距量对EH收集器的效率有着重要影响[17-19].另外,当更多的时隙用于收获时,可以收获更多的能量,从而具有更高的传输概率,但是也增加了迟延.因此,需要研究EH通信系统性能和时隙数量之间的关系,例如Long和Wang等[19-20]针对Rayleigh和Rician衰落信号采用多时隙方案,分析了有效吞吐量以及二进制无线通信的误比特率,得到一些有价值的参考结论.
研究主要贡献总结如下:首先,因为Nakagami-m分布十分适合用来描述城区多径无线信道衰落特性,对观察到的信号的统计特性能够提供更为便利和精确的描述,可以描述Rayleigh信道衰落以及更严重或轻微的信道衰落[24].因此,将EH通信中的通信环境扩展到Nakagami-m无线衰落信道,研究在Nakagami-m衰落信道中采用时间切换多时隙EH方案收集到的随机功率对通信性能的影响.其次,首次推导出了在Nakagami-m衰落信道下时间切换多时隙EH“收集-存储-使用”方案的有效吞吐量和“收集-使用”方案在相干和非相干二进制数字通信的平均误比特率(BER,bit error rate)的精确闭合表达式.最后,通过仿真分析,揭示了在Nakagami-m衰落信道中,上述无线EH通信方案中有效吞吐量和平均误比特率等性能指标和信道衰落条件、EH时隙数和传输延迟、基站发射功率和信号调制解调方式等因素的关系,为实现可靠高效的EH通信系统提供设计依据.
1 EH系统模型考虑一个无线射频EH通信系统,包括一个基站和一个远端设备,以时间切换和半双工模式运行.其中基站首先向远端设备在下行链路传输射频功率,远端设备进行能量收集,然后远端设备仅使用采集到的能量向基站传输数据.假设每一次功率或数据传输都是在一个T s的时隙内完成的.功率传输持续N个时隙,总持续时间为NT s,一个时隙传输功率为Ps.远程设备上的数据传输持续一个时隙,即T s.基于上述假设,EH通信统有2个主要的传输阶段.在第1阶段,基站的功率发射机将射频功率传输到远程设备.远程设备接收的信号可以表示为
| $ {y_i} = {h_i}\sqrt {{P_s}} {x_i} + {n_i} $ | (1) |
其中:i=1, 2, …, I,表明远端设备利用I个时隙进行能量收集;Ps为基站发射功率;xi为基站发送的信号,假设其具有单位功率E{|xi|2}=1;ni为附加复高斯白噪声(AWGN,additive white Gaussian noise),均值为0,方差2β2;hi为基站到远端设备在第i个时隙的信道衰落系数并假设在一个T内平坦,衰落系数hi幅度满足Nakagami-m分布
| $ {f_{{h_i}}}(x) = 2{\left( {\frac{m}{\varOmega }} \right)^m}\frac{{{x^{2m - 1}}}}{{\Gamma (m)}}{\rm{exp}}\left( { - m\frac{{{x^2}}}{\varOmega }} \right),m \ge \frac{1}{2} $ | (2) |
其中:m为Nakagami-m信道衰落参数,m=1时,式(2)变为Rayleigh分布;Ω为信号平均功率;Γ(·)为Gamma函数[21].远端设备接收信号的平均信噪比(SNR,average signal-to-noise ratio)为
| $ \omega = \frac{{\varOmega {P_s}}}{{2{\beta ^2}}} $ | (3) |
采用线性EH收集器对式(1)的信号进行能量收集,则EH收集的总功率为[22]
| $ E = T\sum\limits_{i = 1}^I {{\eta _i}} |{h_i}\sqrt {{P_s}} {x_i}{|^2} = \eta T{P_s}S $ | (4) |
其中:$S=\sum\limits_{i=1}^{I}\left|h_{i} x_{i}\right|^{2}=\sum\limits_{i=1}^{I}\left|h_{i}\right|^{2}$,ηi为EH收集器在第i个时隙的转换效率.如果使用同一个EH收集器,那么ηi=η.
在第2阶段,远程设备使用EH收集的能量将数据传输回基站.基站接收的信号为
| $ y = g\sqrt P x + n $ | (5) |
其中:g为信道衰落,并假设在一个T内为平坦的,同样满足Nakagami-m信道衰落;P为远端设备的发送功率;x为远端设备发送的信号,具有单位功率E{|x|2}=1,n为AWGN,均值为0,方差2β2.远端设备的发送功率来自收集的功率:
| $ P = \frac{E}{T} = \eta {P_s}S $ | (6) |
其中S为一个关于功率的随机变量.因此,整个系统的性能受到信道随机衰落g和随机传输功率P的影响.这是传统通信和EH通信的主要区别.
2 “收集-存储-使用”方案的有效吞吐量吞吐量指标是衡量通信系统性能的重要参数之一,通常是指单位时间内正确传输的信息比特数.在“收集-存储-使用”协议中,远程设备必须等待一定数量的时隙I,用于积累足够的能量,才能执行下一步的信息传输.由于等待时间,EH通信的吞吐量为降为原来的1/(I+1).在实际中为保证一定的服务质量,通常要求发射功率必须大于给定最低传输功率P0,也就是说传输信噪比SNR必须大于门限Λ0=P0/2β2,采用传输概率描述为[19]
| $ {P_{\rm{T}}} = {\rm{Pr}} (P > {P_0}) = {\rm{Pr}} \left( {\frac{P}{{2{\beta ^2}}} = \varLambda > {\varLambda _0}} \right) $ | (7) |
结合传输概率来计算吞吐量的大小,定义EH通信的有效吞吐量为
| $ \tau = \frac{1}{{I + 1}}{P_{\rm{T}}} $ | (8) |
接下来,就需要计算传输概率.这需要Λ的概率密度函数(PDF,probability density function)或累积分布函数(CDF,cumulative density function).若信道衰落hi满足Nakgami-m独立同分布(I.I.D.,independent and identically distributed),那么|hi|2服从Gamma分布
| $ {f_{|{h_i}{|^2}}}(x) = {\left( {\frac{m}{\varOmega }} \right)^m}\frac{{{x^{m - 1}}}}{{\Gamma (m)}}{\rm{exp}}\left( { - m\frac{x}{\varOmega }} \right),m \ge \frac{1}{2} $ | (9) |
已知如果I个独立的Gamma随机变量满足I.I.D.分布,那么它们的和满足参数为Im和IΩ的Gamma分布[23].其PDF为
| $ {f_P}(x) = {\left( {\frac{m}{{\eta {P_s}\varOmega }}} \right)^{Im}}\frac{{{x^{Im - 1}}}}{{\Gamma (Im)}}{\rm{exp}}\left( { - \frac{m}{{\eta {P_s}\varOmega }}x} \right) $ | (10) |
对式(10)进行积分,得其CDF为
| $ {F_P}(x) = \int_0^x {{f_P}} (\alpha ){\rm{d}}\alpha = \gamma ( Im ,\frac{m}{{\eta {P_s}\varOmega }}x){\Gamma ^{ - 1}}(Im) $ | (11) |
其中:γ(a, b)为下不完全Gamma函数[21].最后,结合信噪比门限Λ0=P0/2β2,在Nakagami-m信道衰落环境下“收集-存储-使用”方案的有效吞吐量为
| $ \tau = \frac{1}{{I + 1}}\left\{ {\Gamma \left( {Im,\frac{{m{\varLambda _0}}}{{\eta \omega }}} \right){{[\Gamma (Im)]}^{ - 1}}} \right\} $ | (12) |
其中Γ(a, b)为上不完全Gamma函数[21].
当m=1时,式(11)简化为Rayleigh信道衰落,其PDF和CDF分别为
| $ {{f_P}(x) = \frac{{{x^{I - 1}}}}{{{{(\eta {P_s}\varOmega )}^I}\Gamma (I)}}{\rm{exp}}\left( { - \frac{x}{{\eta {P_s}\varOmega }}} \right)} $ | (13) |
| $ {{F_P}(x) = \gamma (I,x/\eta {P_s}\varOmega ){\Gamma ^{ - 1}}(I)} $ | (14) |
同理,在Rayleigh信道衰落,“收集-存储-使用” EH方案的有效吞吐量为
| $ \tau = \frac{1}{{I + 1}}\left\{ {\Gamma \left( {I,\frac{{{\varLambda _0}}}{{\eta \omega }}} \right){{[\Gamma (I)]}^{ - 1}}} \right\} $ | (15) |
从式(12)和(15)可以看到,系统有效吞吐量τ随着I+1的增加而减小,但是随着上不完全Gamma函数CDF的参数I的增加而增加.因此,一个最佳的I可能存在,在下文的仿真分析中将对此进行详细讨论.
3 “收集-使用”方案的平均误码率在静态AWGN信道中,对于接收信号而言,平均BER取决于所采用的调制和检测方案.对二进制信号而言,如果采用非相干检测方案,BER为
| $ {P_{\rm{e}}}(P,g) = \frac{1}{2}{\rm{exp}}[ - uP(|g{|^2}/2{\beta ^2})] $ | (16) |
而对于相干检测而言,BER为
| $ {P_{\rm{e}}}(P,g) = Q\sqrt {2uP(|g{|^2}/2{\beta ^2})} $ | (17) |
其中:Q(·)为高斯Q函数,u=1为二进制移相键控(BPSK,binary phase shift keying),u=1/2为二进制移频键控(BFSK,binary frequency shift keying)[24].
按照“收集-使用”方案的思想,在I个时隙内远端设备积累的能量需要立即用于传输信息到基站.在“收集-使用”方案中的远端设备到基站的信道衰落|g|2和P都成为随机变量,必须找到两者乘积的分布函数表达式,记为χ=PG,其中G=|g|2/(2β2).在Nakagami-m信道衰落中,G的PDF为
| $ {f_G}(x) = {\left( {\frac{m}{{{\omega _0}}}} \right)^m}\frac{{{x^{m - 1}}}}{{\Gamma (m)}}{\rm{exp}}\left( { - m\frac{x}{{{\omega _0}}}} \right),m \ge \frac{1}{2} $ | (18) |
其中:ω0=Ω0/2β2,因此χ可以计算为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {f_\chi }(z) = \int_0^\infty {{f_p}} (x){f_G}\left( {\frac{z}{x}} \right)\frac{1}{x}{\rm{d}}x = \\ \frac{{2{{\left( {\frac{{{m^2}}}{{\eta {\omega _0}{P_s}\varOmega }}} \right)}^{\frac{{Im + m}}{2}}}}}{{\Gamma (Im)\Gamma (m)}}{z^{\frac{{Im + m - 2}}{2}}}{K_{Im - m}}\left( {2\sqrt {\frac{{{m^2}z}}{{\eta {\omega _0}{P_s}\varOmega }}} } \right) \end{array} $ | (19) |
其中K(I-1)m(·)为(I-1)m阶第二类修正Bessel函数[21],在计算式(19)时使用了文献[21]中的公式3.471.9.
同理,在Rayleigh信道衰落(m=1)环境下,上式可以简化为
| $ {f_\chi }(z) = \frac{{2{{(\eta {\omega _0}{P_s}\varOmega )}^{ - \frac{{I + 1}}{2}}}}}{{\Gamma (I)}}{z^{\frac{{I - 1}}{2}}}{K_{I - 1}}\left( {2\sqrt {\frac{z}{{\eta {\omega _0}{P_s}\varOmega }}} } \right) $ | (20) |
利用式(16)和式(19),得到非相干检测的二进制调制的BER为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_{\rm{e}}} = \int_0^\infty {\frac{1}{2}} {\rm{exp}}( - uz){f_x}(z){\rm{d}}z = \\ \frac{{2{{\left( {\frac{m}{{\sqrt {\eta {\omega _0}{P_s}\varOmega } }}} \right)}^{Im + m}}}}{{\Gamma (Im)\Gamma (m)}}\int_0^\infty {{x^{Im + m - 1}}} {{\rm{e}}^{ - u{x^2}}}{K_{Im - m}}\left( {\frac{{2mx}}{{\sqrt {\eta {\omega _0}{P_s}\varOmega } }}} \right){\rm{d}}x = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left( {\frac{{{m^2}}}{{u\eta {\omega _0}{P_s}\varOmega }}} \right)^{\frac{{Im + m - 1}}{2}}}\frac{{\frac{{{m^2}}}{{{{\rm{e}}^{2u\eta {\omega _0}{P_s}\varOmega }}}}}}{2}{W_{ - \frac{1}{2}(Im + m - 1),\frac{1}{2}(Im - m)}}\left( {\frac{{{m^2}}}{{u\eta {\omega _0}{P_s}\varOmega }}} \right) \end{array} $ | (21) |
其中:Wλ, μ(z)是惠特克(Whittaker)函数[21],在式(21)的推导过程使用了文献[21]中的公式6.631.3.
在Rayleigh信道衰落环境下(m=1),式(21)可以简化为
| $ {P_{\rm{e}}} = \frac{1}{2}\frac{{{{\rm{e}}^{\frac{1}{{2u\eta {\omega _0}{P_s}\varOmega }}}}}}{{{{(u\eta {\omega _0}{P_s}\varOmega )}^{\frac{I}{2}}}}}{W_{ - \frac{I}{2},\frac{I}{2}(I - 1)}}\left( {\frac{1}{{u\eta {\omega _0}{P_s}\varOmega }}} \right) $ | (22) |
对于在Nakagami-m信道衰落环境下的二进制相干检测,平均BER为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_{\rm{e}}} = \int_0^\infty Q (\sqrt {2uz} ){f_\chi }(z){\rm{d}}z = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{2{{\left( {\frac{m}{{\sqrt {\eta {\omega _0}{P_s}\varOmega } }}} \right)}^{Im + m}}}}{{\Gamma (Im)\Gamma (m)}}\left[ {\int_0^\infty {{x^{Im + m - 1}}} {{\rm{K}}_{Im - m}}\left( {\frac{{2mx}}{{\sqrt {\eta {\omega _0}{P_s}\varOmega } }}} \right){\rm{d}}x - } \right.\\ \left. {2\sqrt {\frac{u}{\pi }} \int_0^\infty {{x^{Im + m}}} F\left( {\frac{1}{2},\frac{3}{2}, - u{x^2}} \right){K_{Im - m}}\left( {\frac{{2m}}{{\sqrt {\eta {\omega _0}{P_s}\varOmega } }}x} \right){\rm{d}}x} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} {\frac{1}{2} - \frac{{{{(\eta u{\omega _0}{P_s}\varOmega )}^{\frac{1}{2}}}}}{{\sqrt {\pi m\Gamma (Im)\Gamma (m)} }}\Gamma \left( {Im + \frac{1}{2}} \right)\Gamma \left( {m + \frac{1}{2}} \right) \times }\\ {_3{F_1}\left( {\frac{1}{2},Im + \frac{1}{2},m + \frac{1}{2};\frac{3}{2}; - \frac{{u\eta {\omega _0}{P_s}\varOmega }}{{{m^2}}}} \right)} \end{array} \end{array} $ | (23) |
式(23)在化简过程中,首先,将高斯Q函数进行变量代换改写为补误差函数erfc(·)的形式[21];其次,再进一步进行数学变换为超几何级数pFq(α1, …, αp; β1, …, βq; z)的形式[21];最后结合文献[21]中的公式6.561.16和7.542.4求得平均BER的闭合公式.
同理,在Rayleigh信道衰落(m=1)环境下,式(23)可以简化为
| $ {P_{\rm{e}}} = \frac{1}{2} - \frac{{\Gamma \left( {I + \frac{1}{2}} \right){{\rm{e}}^{\frac{1}{{2u\eta {\omega _0}{P_s}\varOmega }}}}}}{{2{{(u\eta {\omega _0}{P_s}\varOmega )}^{\frac{{I - 1}}{2}}}\Gamma (I)}}{W_{ - \frac{I}{2},\frac{I}{2}}}\left( {\frac{1}{{u\eta {\omega _0}{P_s}\varOmega }}} \right) $ | (24) |
从式(21)~(24)可以看到,通信性能指标BER不但受制于信道条件、发射功率和调制方式,还与所选择的时隙数密切相关,需要针对具体通信中的实际环境,选择最佳时隙实现BER最小.
4 仿真分析根据第3节得到的有效吞吐量和平均BER的理论闭合公式,研究分析典型仿真条件下,对EH通信性能产生重要影响的因素.在以下仿真例子中,设置门限Λ0的取值从0~20 dB,间隔大小为1 dB.时隙数I从1~20,间隔数为1,定义基站接收信噪比ω=ω0PsΩ,能够反映基站发送功率Ps的大小,取值从0~20 dB,间隔1 dB.和实际情况相结合,设置EH收集器在每个时隙的转换效率均为η=0.5.在图 1~图 6中,设置信道的仿真条件为m的Nakagami-m衰落,当m=1时退化为Rayleigh衰落.
|
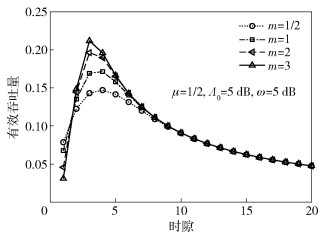
图 1 有效吞吐量和衰落参数之间的关系 |
|
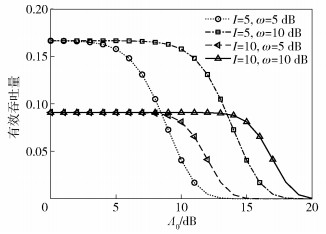
图 2 有效吞吐量和门限信噪比之间的关系 |
|
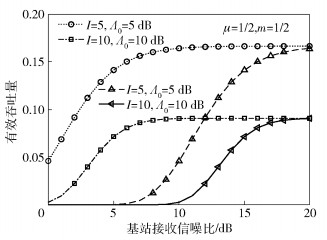
图 3 有效吞吐量和信噪比之间的关系 |

|
图 4 平均误比特率和信道衰落参数之间的关系 |

|
图 5 平均误比特率和EH时隙之间的关系 |
|
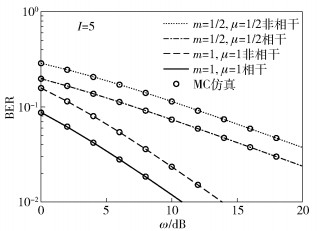
图 6 平均误比特率和信噪比之间的关系 |
图 1~图 3显示了在EH通信采用“收集-存储-使用”方案中Nakagami-m信道衰落系数m、信噪比ω及门限信噪比Λ0对有效吞吐量τ的影响. 图 1显示EH通信有效吞吐量τ和信道衰落参数m之间的关系,在给定条件μ=1/2,Λ0=5 dB及ω=5 dB,存在使得EH通信具有最大有效吞吐量的最佳时隙,如m=1/2和m=1最佳时隙数I=4,当m=2和m=3时的最佳时隙数I=3.在时隙数小于最佳时隙数,有效吞吐量随着时隙数的增加而增加,在时隙数大于最佳时隙数,有效吞吐量随着时隙数的增加而减小.比较不同的衰落参数m,可以发现一般情况下,信道衰落小则有效吞吐量大,可以收集更多的能量和具有更小的传输迟延.需要注意的是,在上述设置的仿真条件下,当取一个时隙进行能量收集,信道衰落小的EH通信的有效吞吐量反而小于信道衰落大的EH通信的有效吞吐量,这可以根据衰落的功率CDF满足Gamma分布进行解释,即相比小衰落条件,在大衰落条件下,EH收集器在一个时隙具有更大的概率收集到相同的功率. 图 1中显示,在时隙数不断增加时,各条有效吞吐量曲线趋于重合,这是因为从式(12)可以得到当I→∞时,τ→1/(I+1),而与其他参数取值无关.
图 2清楚地显示出有效吞吐量和门限信噪比Λ0之间的关系.首先,可以看到起初EH通信的有效吞吐量保持一个常数;然后随着Λ0的增大而急剧降低,说明需要针对“收集-存储-使用”EH通信方案设置合理的Λ0.如在图 2中,对于I=5和ω=5 dB,Λ0不大于4 dB;I=5和ω=10 dB,Λ0不大于9 dB,不一而述.其次,图中显示,在相同的信道衰落和平均接收功率条件下,大的时隙数意味着高迟延,导致有效吞吐量降低,但也和Λ0密切相关,如I=5和ω=5 dB在Λ0不大于8 dB的有效吞吐量高于I=10和ω=5 dB对应的有效吞吐量,但是Λ0一旦高于8 dB,情形刚好相反.
图 3所示为EH有效吞吐量和基站接收信噪比ω之间的关系.随着ω的增加,EH能够急剧地增加有效吞吐量.但同时也应该注意到,随着ω的增加,存在相同的有效吞吐量上限,这里称为“天花板”效应.天花板高度是由时隙数I和信噪比门限Λ0决定,不再随着ω的持续增加而增加,如I=5和Λ0=10 dB,τ=0.175;I=10和Λ0=20 dB,τ=0.085.这就意味着,传统意义上采用增加发射功率的方式增加有效吞吐量的方式在EH通信中不再有效,需要结合信道衰落条件、门限信噪比和恰当的时隙数来使得EH通信实现最佳有效吞吐量.
图 4~图 6所示为EH通信采用“收集-使用”方案中信道衰落程度、时隙数以及基站发射信噪比等参数对平均误比特率的影响.为了保证理论结论和实际EH模型结论能够互相验证,蒙特卡罗(MC,Monte Carlo)仿真结果也同时在图中同时显示.图中显示仿真次数为106时的MC仿真结果和数值仿真结果拟合特性完全一致.
图 4所示为EH通信平均误比特率和Nakagami-m信道衰落参数m之间的关系,m≥1/2.若m=1,Nakagami-m变成Rayleigh衰落.图中标示的参数μ=1/2为BFSK调制,而μ=1为BPSK调制的EH通信. 图 4显示,对于具有相同时隙数、基站发射信噪比和相同转换效率,EH通信的误码率随着信道条件的改善(m增大)而降低,说明良好的信道衰落环境不但有利于EH通信中基站能量信号发送给远端的设备用于能量收集而且有利于远端设备发送信息返回给基站.图中也显示,BPSK调制优于BFSK调制且相干检波优于非相干检波.在相同的工作条件下,EH通信中采用相干检波的BPSK调制具有更好的通信性能.
图 5所示为EH通信平均误比特率和EH时隙数I之间的关系,仿真环境包括典型的Makagami-m衰落和Rayleigh衰落、相干和非相干的BPSK及BFSK解调方式. 图 5中显示的仿真曲线具有下凸特性,说明随着I的增加,平均BER起初下降较快,随后变得平缓,即平均BER性能不能随着I的增加而线性增加,不断地增大I并不能有效改善BER性能,反而使得通信迟延增加.此外,“收集-使用”方案需要使用超级电容作为储能器件,超级电容的优点是具有较大的瞬时容量,缺点是随着时延会产生较大的能量泄露,因此要求EH时隙数尽可能小.对于图中预设参数条件下,非相干解调的时隙数不大于5,而对于相干解调EH时隙数不大于10,则可较好地平衡EH通信中的平均BER和迟延.
图 6显示了EH通信平均误比特率BER和基站接收信噪比ω之间的关系.对于不同的Nakagami-m衰落参数m以及相干或者非相干调制解调方案,平均误比特率BER随着基站接收信噪比ω的增大而减小,这与期望一致.因为在EH时隙数I一定的情况下,基站接收信噪比ω和基站发送功率的大小有关.持续增加基站用于远端设备进行能量收集的信号功率,按照“收集-使用”方案,远端设备能够收集到更多的能量用于数据的发送,降低基站接收到的平均BER.
5 结束语研究了在Nakagmi-m信道衰落下采用多时隙EH结合“收集-存储-使用”和“收集-使用”方案的无线通信性能,研究指标包括有效吞吐量和平均误比特率等,并从数学上理论推导出精确的闭合公式.仿真结果表明,多时隙EH通信的性能受到时隙数、信道条件、基站发射功率和能量转换效率等参数的影响.对于“收集-存储-使用”的EH方案,存在最佳的能量收集时隙数用来平衡传输概率和延迟,以实现最佳有效吞吐量,持续增加基站的发射功率并不能够增加EH无线通信的有效吞吐量,存在“天花板”效应.而在“收集-使用”的EH方案时,应该使用少量时隙来平衡误码率性能和多时隙EH带来的迟延,而持续增加基站的发射功率有利于降低接收到的平均误比特率.
| [1] |
Ku Menglin, Wei Li, Yan Chen, et al. Advances in energy harvesting communications:past, present, and future challenges[J]. IEEE Communications Surveys and Tutorials, 2016, 18(2): 1384-1412. DOI:10.1109/COMST.2015.2497324 |
| [2] |
Hall C, Lau D, Lennon A, et al. Hybrid solar energy harvesting and storage devices:the promises and challenges[J]. Materials Today Energy, 2019, 13(1): 22-44. |
| [3] |
Lu X, Wang P, Niyato D, et al. Wireless networks with RF energy harvesting:a contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 757-789. |
| [4] |
Babaei M, Aygolu U, Basar E. BER analysis of dual-hop relaying with energy harvesting in Nakagami-m fading channel[J]. IEEE Transactions on Wireless Communications, 2018, 17(7): 4352-4361. DOI:10.1109/TWC.2018.2823711 |
| [5] |
Le P N. Throughput analysis of power-beacon assisted energy harvesting wireless systems over non-identical Nakagami-m fading channels[J]. IEEE Communications Letters, 2018, 22(4): 840-843. DOI:10.1109/LCOMM.2017.2756053 |
| [6] |
Huang K, Lau V. Enabling wireless power transfer in cellular networks:architecture, modeling and deployment[J]. IEEE Trans Wireless Communication, 2012, 13(2): 902-912. |
| [7] |
Pinuela M, Mitcheson P D, Lucyszyn S. Ambient RF energy harvesting in urban and semi-urban environments[J]. IEEE Trans Microwave Theory Technology, 2013, 61(7): 2715-2726. DOI:10.1109/TMTT.2013.2262687 |
| [8] |
Huang Jun, Xing Congcong, Wang Chonggang. Simultaneous wireless information and power transfer:technologies, applications, and research challenges[J]. IEEE Communications Magazine, 2017, 55(11): 26-32. DOI:10.1109/MCOM.2017.1600806 |
| [9] |
Hassani S E, Hassani H E, Boutammachte N. RF energy harvesting for 5G: an overview[C]//2017 International Renewable and Sustainable Energy Conference. Tangier: IEEE Press, 2017: 1-6.
|
| [10] |
Ye Jia, Liu Zhedong, Zhao Hui, et al. Relay selections for cooperative underlay CR systems with energy harvesting[J]. IEEE Trans Cognitive Communications and Networking, 2019, 5(2): 358-369. DOI:10.1109/TCCN.2019.2908900 |
| [11] |
Leng S Y, Yener A. Age of information minimization for an energy harvesting cognitive radio[J]. IEEE Trans Cognitive Communications and Networking, 2019, 5(2): 427-439. DOI:10.1109/TCCN.2019.2916097 |
| [12] |
Ercan A, Sunay M, Akyildiz L F. RF energy harvesting and transfer for spectrum sharing cellular iot communications in 5G systems[J]. IEEE Trans Mobile Computing, 2018, 17(7): 1680-1694. DOI:10.1109/TMC.2017.2740378 |
| [13] |
Ye Yinghui, Li Yongzhao, Zhou Fuhui, et al. Power splitting-based SWIPT with dual-hop DF relaying in the presence of a direct link[J]. IEEE Systems Journal, 2019, 13(2): 1316-1319. DOI:10.1109/JSYST.2018.2850944 |
| [14] |
Yuan Fangchao, Zhang Q T, Shi Jin, et al. Optimal harvest-use-store strategy for energy harvesting wireless systems[J]. IEEE Trans Wireless Communications, 2015, 14(2): 698-710. DOI:10.1109/TWC.2014.2358215 |
| [15] |
Siddiqui A M, Musavian L, Ni Q. Energy efficiency optimization with energy harvesting using harvest-use approach[C]//2015 IEEE International Conference on Communication Workshop. London: IEEE Press, 2015: 1982-1987.
|
| [16] |
Chen Y, Zhao N, Alouini M S. Wireless energy harvesting using signals from multiple fading channels[J]. IEEE Trans Communications, 2017, 65(11): 5027-5039. DOI:10.1109/TCOMM.2017.2734665 |
| [17] |
Cao Ning, Hu Yifan, Wu Feng, et al. Analysis of discrete-time energy-harvesting DF relay in Rician fading channel[C]//2017 Progress in Electromagnetics Research Symposium. Petersburg: IEEE Press, 2017: 3006-3011.
|
| [18] |
Bao V N Q, Toan H V, Le K N. Performance of two-way AF relaying with energy harvesting over Nakagami-m fading channels[J]. IET Communications, 2018, 12(20): 2592-2599. DOI:10.1049/iet-com.2018.5090 |
| [19] |
Long Min, Chen Yunfei. Performance analysis of energy harvesting communications using multiple time slots[J]. IET Communications, 2019, 13(3): 289-296. DOI:10.1049/iet-com.2018.5210 |
| [20] |
Wang Mingwei. Comments on "performance analysis of energy harvesting communications using multiple time slots"[J]. IET Communications, 2019, 13(20): 3601. DOI:10.1049/iet-com.2019.0449 |
| [21] |
Gradshteyn I S, Ryzhik I M. Table of integrals, series, and products[M]. 8th ed. San Diego: Academic Press, 2014.
|
| [22] |
Gu Y J, Sonia A. RF-based energy harvesting in decode-and-forward relaying systems:ergodic and outage capacities[J]. IEEE Trans Wireless Communications, 2015, 14(11): 6425-6434. DOI:10.1109/TWC.2015.2453418 |
| [23] |
Nakagami M, GHoffman W. 'The m-distribution:a general formula of intensity distribution of rapid fading' in statistical methods in radio wave propagation[M]. Oxford: Pergamon Press, 1960: 3-36.
|
| [24] |
Proakis J G, Salehi M. Digital communications[M]. New York: McGraw-Hill, 2007: 841-848.
|


