2. 上海霍普建筑设计事务所股份有限公司, 上海 200135
为辅助设计师排布外轮廓形状复杂、面积大、障碍物多的大规模地下车库,针对局部复杂轮廓内同向车位与车道共同优化排布问题,提出了基于图形分割的混合整数线性规划模型.考虑了车位排列角度及位置的优化,能够处理任意轮廓内的车位与车道排布.开发了基于粒子群优化的分解算法,并通过实际的工程图纸验证了模型和算法的有效性.结果表明,该算法能快速有效地排布局部车位,辅助设计者给出最佳优化排布方案.开发的可视化及人机交互功能可大大提高设计者的开发效率.
2. Shanghai HYP-ARCH Architectural Design Consultant Commoney Limited, Shanghai 200135, China
To assist designers in designing large-scale urban underground parking lots characterized by irregular contour, large area and various obstacles, a mixed integer linear program model based on polygon decomposition is proposed to optimize the allocation of parking lots and roads together in the same direction within local irregular contours.This model not only considers the optimization of parking angles and position, but also has the ability to deal with the designing of parking lots and roads in contours of arbitrary shape.A decomposition method based on particle swarm optimization algorithm is presented to solve the model and engineering drawings were used to validate its efficiency.It is shown that the proposed method can arrange local irregular contours efficiently and help designers to find the optimal design of parking lots.Via visualization and human-computer interaction, the designers' development efficiency can be largely improved.
随着我国经济的持续快速发展,城市汽车数量大幅增加,“停车难”成了城市发展的瓶颈[1].优化建设城市地下停车场、在有限空间排出最多车位是解决“停车难”问题的有效途径[2].因此,合理高效地设计地下车库,减少浪费面积,能有效降低地下车库的建设成本,提高停车空间的利用率,这对于我国人口密度大、寸土寸金的大城市如上海、北京等尤其重要.然而,受限于地块形状及地上建筑结构的要求,城市地下车库往往具有外轮廓形状复杂、面积大、障碍物多、车位及车道设计复杂等特点,这些给城市地下车库的优化设计带来了巨大挑战[3].
现有的车位排布问题的研究对象主要为轮廓简单、不带障碍的普通停车场或高密度停车场.针对普通矩形停车场,Abdelfatah等[4]提出了一种考虑了不同车位与车道夹角的停车位设计线性规划模型;Kong等[5]考虑了车位大小可变的情况,通过混合整数非线性模型研究了车位大小改变对停车场车位数量的影响;Huang等[6]设计了一套基于模拟退火算法的矩形停车场排布问题的通用算法;针对普通三角形停车场,Syahrini等[7]同样以车位与车道夹角为决策变量、以最大化车位数为目标建立了线性规划模型;针对平行四边形停车场的排布问题,Ihda等[8]提出了一种线性规划模型;针对矩形高密度停车场,Ferreira等[9]设计了一种车位平行叠放的排车方式;Timpner等[10]提出了停车空间优化模型;Banzhaf等[11]对普通停车场改造为高密度停车场问题构建了混合整数规划模型;Nourinejad[12]等使用排队论构建了混合整数模型,并同时用benders分解算法进行求解.然而,很多学者都没有考虑轮廓复杂、带障碍物的城市地下停车场排布问题,无法自适应地对复杂轮廓进行转化.此外,出于地下车库柱网设计及实用性的要求,其停车位不能倾斜于车道,也不适合密集摆放.因此,不同于传统侧重于研究车位与车道夹角的优化及车位密集摆放方式的停车场设计问题,车位空间排列方式,即排车区域的划分、整排车的排车角度及排车起始位置,才是城市地下停车场车位排布的关键.
为辅助设计师排布大规模地下车库,针对局部复杂轮廓内同向的车位与车道共同优化排布问题,提出了一种基于图形分割的混合整数线性规划模型.该模型具有以下性能:①能够自适应地对任意复杂轮廓进行转化;②能够决策复杂轮廓内部整排车位的排车角度及排车起始位置;③能够通过基于粒子群算法的分解算法高效地求解,并通过可视化直观地给出排布方案.
1 问题描述城市地下车库车位排布问题可归为在给定外轮廓及障碍物情况下,最大化车位排布数量问题.该问题的主要特点及难点可归纳如下.
1) 车库面积大,可排车位数量多,且外轮廓复杂,存在斜边,外轮廓内有形状不一的障碍.
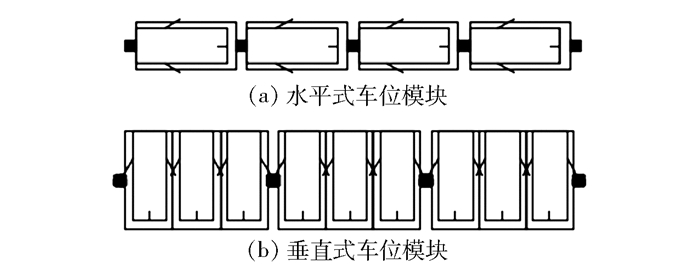
2) 排车方式多样.地下车库出于承重柱设计及后续设施布置的要求,其排车方法分平行式及垂直式,如图 1所示.其中,平行式只用于沿墙排车.
|
图 1 车位模块类型示意图 |
3) 除需要保证车位模块与车位模块、车位模块与车道之间的不重叠之外,还需要保证车道能够构成连通的网络,同时需要考虑不同转角对应的最小转弯半径.
4) 承重柱分布有距离限制,且需要在大范围内保证柱网对齐,以减小建设成本.
针对上述特点及难点,徐等[13]提出了一种三阶段排车方法,如图 2所示.

|
图 2 三阶段排车方法示意图 |
第1阶段:沿外轮廓及障碍对车位模块进行排布;
第2阶段:根据第1阶段形成的车道对剩余空白区域进行最优划分;
第3阶段:在第2阶段给出的区域内部对车位模块进行排布,并可视化结果,与CAD对接.
针对第1阶段问题,徐等[13]构建了基于遗传算法(GA,genetic algorithm)的外圈排布算法,这里主要关注于第3阶段问题的建模与求解.
第3阶段为局部复杂轮廓内同向的车位与车道共同优化排布问题,作为三阶段排车方法中前两阶段的底层,是本问题的核心难点之一.一方面,该问题的轮廓输入由第2阶段给出,具有一定的复杂性及任意性,需进行转化;另一方面,前两阶段的计算依赖于该问题的求解,模型需要被频繁调用,因此必须要有很高的计算效率及求解精度.
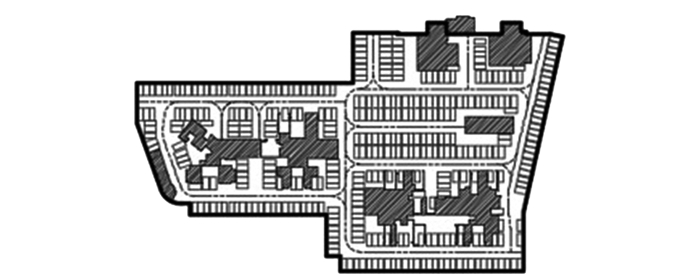
2 模型建立在图 3所示的地下车库中,局部复杂轮廓内同向的车位与车道共同优化排布问题可归纳如下.
|
图 3 地下车库轮廓示意图 |
给定由车道围成的区域外轮廓,其中需要同向紧密排列若干列车位模块.按垂直于车位模块方向建立坐标系,记按顺序记录的车道内轮廓端点集合为{(aw, dw)}w∈ZW,ZW={1, 2, …, W},W为端点个数.其中,首个端点与最后一个端点重合,即a1=aW, d1=dW;记区域内部整列车位模块下标集合为P,每列车位模块中单个车位模块的下标集合为Q.模型的目标是最优化车位模块的排布,使车位模块的总长度最长.
该问题建模的关键在于复杂轮廓的数学表示.在计算机中,复杂轮廓是用轮廓端点集合存储的.然而,这种表示方式无法直接做混合整数线性规划模型的参数,因此需要将其进行转化.图形分割是解决该问题的有效途径.扫描线算法是计算机图形学中的常用算法,广泛应用于图形求交、图形划分等领域[14-15].基于扫描线算法的原理,设计了高效的图形分割算法,将由轮廓端点集合表示的复杂轮廓转化为模型参数, 图形分割算法见附录.所使用的符号如下.
1) 参数
ρ:单个车位的长度,即车位模块的宽度;
σ:道路的宽度;
M:一个足够大的数;
ε:一个足够接近于零的正数;
n:由垂直于x轴的扫描线所构成的横坐标区间数量;
m:2条扫描线之间的最大子区域数量;
ui:扫描线横坐标,i∈In+1, In+1={1, 2, …, n, n+1};
vij:横坐标为ui扫描线所对应的第j个纵坐标区间下边界,i∈In,j∈Jm, Jm={1, 2, …, m};
vij:横坐标为ui的扫描线所对应的第j个纵坐标区间上边界,i∈In,j∈Jm;
kij:横坐标为ui及ui+1扫描线之间第j个子区域下边界所对应的分界线斜率,i∈In,j∈Jm;
bij:横坐标为ui及ui+1扫描线之间第j个子区域下边界所对应的分界线截距,i∈In,j∈Jm;
kij:横坐标为ui及ui+1扫描线之间第j个子区域上边界所对应的分界线斜率,i∈In,j∈Jm;
bij:横坐标为ui及ui+1扫描线之间第j个子区域上边界所对应的分界线截距,i∈In,j∈Jm.
2) 决策变量
xp:第p列车位模块左下角横坐标,xp∈
δp:第p列车位模块左下角横坐标是否超出区域轮廓端点横坐标最小值,δp∈{0, 1},p∈P;
δp:第p列车位模块右下角横坐标是否超出区域轮廓端点横坐标最大值,δp∈{0, 1}, p∈P;
γpi:第p列车位模块左下角横坐标是否在ui右侧,γpi∈{0, 1}, p∈P, i∈In;
γpi:第p列车位模块左下角横坐标是否在ui+1左侧,γpi∈{0, 1}, p∈P, i∈In;
γ′pi:第p列车位模块右下角横坐标是否在ui右侧,γ′pi∈{0, 1}, p∈P, i∈In;
γ′pi:第p列车位模块右下角横坐标是否在ui+1左侧,γ′pi∈{0, 1}, p∈P, i∈In;
γ″pi:ui是否在第p列车位模块左下角横坐标右侧,γ″pi∈{0,1}, p∈P, i∈In;
γ″pi:ui是否在第p列车位模块右下角横坐标左侧,γ″pi∈{0, 1}, p∈P, i∈In;
ypq:第p列第q个车位模块左下角纵坐标,ypq∈
lpq:第p列第q个车位模块长度,lpq∈
βpqij:第p列第q个车位模块左边界线是否在横坐标为ui及ui+1的扫描线之间的第j个子区域内,βpqij∈{0, 1}, p∈P, q∈Q, i∈In, j∈Jm;
β′pqij:第p列第q个车位模块右边界线是否在横坐标为ui及ui+1的扫描线之间的第j个子区域内,β′pqij∈{0, 1}, p∈P, q∈Q, i∈In, j∈Jm;
β″pqij:第p列第q个车位模块上下端点是否在横坐标为ui的扫描线所对应的第j个纵坐标区间内,β″pqij∈{0, 1}, p∈P, q∈Q, i∈In, j∈Jm.
3) 局部轮廓内车位模块排布模型
建立混合整数线性规划模型如下:
| $ {\rm{max}}\sum\limits_{p \in P,q \in Q} {{l_{pq}}} $ | (1) |
| $ {x_p} = {x_1} + (p - 1)\rho + {\rm{ floor }}[0.5(p - 1)]\sigma ,\forall p \in P $ | (2) |
| $ {{y_{pq}} + {l_{pq}} \le {y_{p(q + 1)}},\forall p \in P,q \in Q} $ | (3) |
| $ {{x}_{p}}\ge {{u}_{1}}-M{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\delta }{_{p}}},\forall p\in P $ | (4) |
| $ {{l}_{pq}}\le M(1-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\delta }{_{p}}}),\forall p\in P $ | (5) |
| $ {{x}_{p}}+\rho \le {{u}_{n+1}}+M{{{\bar{\delta }}}_{p}},\forall p\in P $ | (6) |
| $ {{l}_{pq}}\le M(1-{{{\bar{\delta }}}_{p}}),\forall p\in P $ | (7) |
| $ {{x}_{p}}+\varepsilon \le {{u}_{i}}+M{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}}},\forall p\in P,i\in {{I}_{n}} $ | (8) |
| $ {{x}_{p}}-\varepsilon \ge {{u}_{i+1}}-M{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}}},\forall p\in P,i\in {{I}_{n}} $ | (9) |
| $ \begin{matrix} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}{{}_{i*j}}}{{x}_{p}}+{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}{{}_{i*j}}}-M(3-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}}}-{{{\bar{\gamma }}}_{pi}}-{{\beta }_{pqij}})\le {{y}_{pq}}, \\ \forall p\in P,q\in Q,i\in {{I}_{n}},j\in {{J}_{m}} \\ \end{matrix} $ | (10) |
| $ \begin{array}{*{35}{l}} {{y}_{pq}}+{{l}_{pq}}\le {{{\bar{k}}}_{ij}}{{x}_{p}}+{{{\bar{b}}}_{ij}}+M(3-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}}}-{{{\bar{\gamma }}}_{pi}}-{{\beta }_{pqij}}), \\ \ \ \ \ \ \ \ \ \forall p\in P,q\in Q,i\in {{I}_{n}},j\in {{J}_{m}} \\ \end{array} $ | (11) |
| $ \sum\limits_{j\in {{J}_{m}}}{{{\beta }_{pqj}}}=1,\forall p\in P,q\in Q,i\in {{I}_{n}} $ | (12) |
| $ {{x}_{p}}+\rho +\varepsilon \le {{u}_{i}}+M{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}^{\prime }}},\forall p\in P,i\in {{I}_{n}} $ | (13) |
| $ {{x}_{p}}+\rho -\varepsilon \ge {{u}_{i+1}}-M\bar{\gamma }_{pi}^{\prime },\forall p\in P,i\in {{I}_{n}} $ | (14) |
| $ \begin{matrix} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}{{}_{i*j}}}({{x}_{p}}+\rho )+{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}{{}_{i*j}}}-M(3-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}^{\prime }}}-\bar{\gamma }_{pi}^{\prime }-\beta _{pqij}^{\prime })\le {{y}_{pq}}, \\ \forall p\in P,q\in Q,i\in {{I}_{n}},j\in {{J}_{m}} \\ \end{matrix} $ | (15) |
| $ \begin{matrix} {{y}_{pq}}+{{l}_{pq}}\le {{{\bar{k}}}_{ij}}({{x}_{p}}+\rho )+{{{\bar{b}}}_{ij}}+M(3-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}^{\prime }}}-\bar{\gamma }_{pi}^{\prime }-\beta _{pqij}^{\prime }), \\ \forall p\in P,q\in Q,i\in {{I}_{n}},j\in {{J}_{m}} \\ \end{matrix} $ | (16) |
| $ \sum\limits_{j\in {{J}_{m}}}{\beta _{pqij}^{\prime }}=1,\forall p\in P,q\in Q,i\in {{I}_{n}} $ | (17) |
| $ {{u}_{i}}+\varepsilon \le {{x}_{p}}+M{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}^{\prime \prime }}},\forall p\in P,i\in {{I}_{n}} $ | (18) |
| $ \quad {{u}_{i}}-\varepsilon \ge {{x}_{p}}+\rho -M\bar{\gamma }_{pi}^{\prime \prime },\forall p\in P,i\in {{I}_{n}} $ | (19) |
| $ \begin{matrix} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}{{}_{i*j}}}-M(3-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}^{\prime \prime }}}-\bar{\gamma }_{pi}^{\prime \prime }-\beta _{pqij}^{\prime \prime })\le {{y}_{pq}}, \\ \forall p\in P,q\in Q,i\in {{I}_{n}},j\in {{J}_{m}} \\ \end{matrix} $ | (20) |
| $ \begin{matrix} {{y}_{pq}}+{{l}_{pq}}\le {{{\bar{v}}}_{ij}}+M(3-{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma }{_{pi}^{\prime \prime }}}-\beta _{pqij}^{\prime \prime }), \\ \forall p\in P,q\in Q,i\in {{I}_{n}},j\in {{J}_{m}} \\ \end{matrix} $ | (21) |
| $ \sum\limits_{j\in {{J}_{m}}}{\beta _{pqij}^{\prime \prime }}=1,\forall p\in P,q\in Q,i\in {{I}_{n}} $ | (22) |
模型目标为最大化区域内车位模块总长度.约束(2)保证了所有车位模块同向紧密排列,“floor()”为向下取整.约束(3)保证了同一列车位模块之间互不重叠,即第p列第q个车位模块的上边界纵坐标值ypq+lpq小于在第q+1个车位模块下边界纵坐标值yp(q+1).约束(4)~(7)将最左侧及最右侧无法排布进区域内部的车位模块长度置零.其中,约束(4)和(5)保证了当第p列车位模块左下角坐标小于区域轮廓顶点横坐标最小值时,将第p列所有车位模块置零,即当δp为0时,必须满足xp≥u1,当δp为1时,必须满足lpq≤0;类似地,约束(6)和(7)保证了当第p列车位模块右下角坐标大于区域轮廓顶点横坐标最大值时,将第p列所有车位模块长度置零.约束(8)~(22)将有效的车位模块约束在区域内.其中,约束(8)~(12)保证了车位模块左边界在区域轮廓内.当第p列第q个车位模块的左下角横坐标xp不在ui及ui+1之间,即xp≤ui或xp≥ui+1时,γpi及γpi可以不同时等于1,此时约束(10)~(12)不起作用;而当ui < xp < ui+1时,γpi及γpi必须同时为1,此时,约束(10)~(12)保证了车位模块上下边界必须在横坐标为ui及ui+1的扫描线之间的某个子区域内,即βpqij等于1时,必须同时满足kijxp+bij≤ypq及ypq+lpq≤kijxp+bij.类似地,约束(13)~(17)保证了车位模块右边界在区域轮廓内,约束(18)~(22)保证了当车位模块横跨2个不同区域轮廓子轮廓时,分界线与车位模块交点在区域轮廓内.
3 算法设计区域内车位排布问题关键在于车位模块横坐标xp的确定.给定xp∈{z|u1≤z≤un+1-ρ},记车位模块上下边界对应的区间为Bpq={z|ypq≤z≤ypq+lpq},则Bpq的长度即为车位模块长度lpq.记任意一点z∈Bpq,区间集合Dip、D′ip、D″ip,则约束(8)~(12)可写为
| $ \begin{matrix} z\in {{D}_{ip}}=\bigcup\limits_{j\in {{J}_{m}}}{\{z|{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}{{}_{i*j}}}{{x}_{p}}+{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}{{}_{i*j}}}\le z\le {{{\bar{k}}}_{ij}}{{x}_{p}}+{{{\bar{b}}}_{ij}}\}} \\ \forall i\in \{i|{{u}_{i}}\le {{x}_{p}}\le {{u}_{i+1}},i\in {{I}_{n}}\} \\ \end{matrix} $ | (23) |
类似地,约束(13)~(17)及(18)~(22)可写为
| $ \begin{array}{*{35}{l}} z\in D_{ip}^{\prime }=\bigcup\limits_{j\in {{J}_{m}}}{\{z|{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}{{}_{ij}}}({{x}_{p}}+\rho )+{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}{{}_{ij}}}\le z\le {{{\bar{k}}}_{ij}}({{x}_{p}}+\rho )+{{{\bar{b}}}_{ij}}\}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \forall i\in \{i|{{u}_{i}}\le ({{x}_{p}}+\rho )\le {{u}_{i+1}},i\in {{I}_{n}}\} \\ \end{array} $ | (24) |
| $ \begin{matrix} z\in D_{ip}^{\prime \prime }=\bigcup\limits_{j\in {{J}_{m}}}{\{z|{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}{{}_{ij}}}\le z\le {{{\bar{v}}}_{ij}}\}}, \\ \forall i\in \{i|{{x}_{p}}\le {{u}_{i}}\le {{x}_{p}}+\rho ,i\in {{I}_{n}}\} \\ \end{matrix} $ | (25) |
对足够多的每列车位模块数, 第p列车位模块总长度
由约束(2), 车位模块横坐标xp的优化等价于第1列车位模块横坐标x1的优化,是连续非凸优化问题.对于该类问题,在启发式算法中,相比于离散编码的GA[16-17],直接对连续变量进行编码的粒子群优化(PSO,particle swarm optimization)算法[18-19]具有很强的优势.因此,采用PSO算法优化第1列车位模块横坐标x1.
4 实例验证使用10张实际工程图纸中的局部区域轮廓对模型进行验证及可视化.其中,道路宽度设置为5 500 mm,车位长度为5 300 mm,车位宽度为2 400 mm,承重柱宽度为600 mm.实验环境为4核、内存16 GB、处理器主频为3.4 GHz的计算机,基于Matlab编程环境、Yalmip计算平台及Gurobi求解器.设PSO最大迭代次数T为20、30、60,种群数S为20、30、40,冲量权重ω为0.6、0.7、0.8进行正交实验,最终选取最大迭代次数T为30,种群数S为20,冲量权重ω为0.7.加速度常数c1、c2根据经验设置为2,粒子位置极值Lmin、Lmax分别设为u1-2ρ-σ及u1, 速度极值设为2ρ+σ的正负0.6倍.用于对比的GA方面,同样通过正交实验,最终选取最大迭代次数T为30,种群数S为20,交叉率为0.8,变异率为0.2,并使用十位二进制编码将搜索范围等间距离散化.
4.1 算法有效性为验证算法有效性,对比了Gurobi求解器、GA及PSO算法的结果,如表 1所示.可看出,随图纸规模的增大及复杂度的增加,求解器的求解时间增加较快,而GA及PSO算法的求解时间保持在2 s内.求解效果方面,PSO算法与求解器结果基本一致.而GA由于离散编码,计算较大规模图纸时会忽略部分最优解,导致效果不如PSO算法.
|
|
表 1 局部区域轮廓计算结果 |
从三阶段排车方法整体求解角度,由于模型为大量调用的底层函数,使用求解器求解会导致整体算法求解时间上的不稳定,尤其对复杂图纸,整体求解时间过长,无法在合理时间内给出结果;而PSO算法求解结果在排法上与最优解保持一致,求解效果好于GA,效率高而稳定,能很好地服务于整体的求解.
从单独作为一个模块辅助设计师排布的角度,使用Gurobi求解器求解模型会大大延长对复杂轮廓的计算时间,无法适应设计师快速迭代设计方案的需要;而使用PSO算法进行求解能在设计师绘制出局部的任意辅助轮廓后快速排布,满足实用性要求.
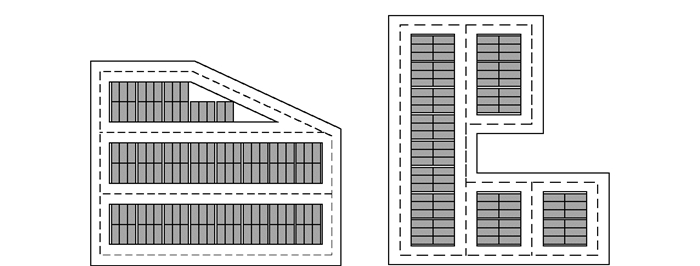
4.2 模型有效性为验证模型的有效性,对图纸的求解结果进行可视化. 图 4展示了典型的五边形及C形轮廓的排布结果.可看到,模型很好地对五边形及C形的轮廓进行了排布,排布结果与设计师的常用排法一致.其中,五边形遍历了4种角度,C形遍历了2种角度.
|
图 4 局部区域排布情况示意图 |
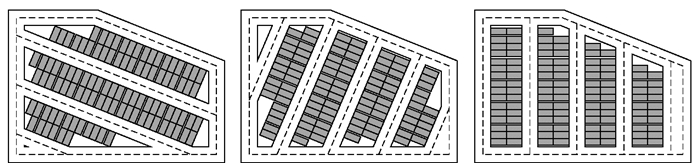
图 5展示了排五边形时另外3种角度对应的最优解.对应有效车位模块总长为276 402 mm、269 525 mm及301 324 mm,对应总车位数分别为102、98及111.其中,第1和第3种也是设计师常用的排布方案,但由于实际工作量的限制,设计师往往无法遍历所有可能的情况,有时会陷入第1或3种排布方案的局部最优解.而使用模型对局部进行排布, 通过算法保证区域内的排法是设计师常用排法中的最优排法,能使设计师集中于区域整体形状的设计,从而提高设计师的设计效率.另外,结合所提出的三阶段排车方法,能够实现对地下车库整体方案的自动排布.
|
图 5 五边形区域排布情况示意图 |
针对城市地下车库车位排布问题,建立了混合整数线性规划模型,开发了基于PSO算法的分解算法对模型进行求解,并使用工程图纸对所提出模型的有效性进行了验证,对排车结果进行了可视化.得到以下结论:①针对局部复杂轮廓内同向的车位与车道共同优化排布问题,创新性地结合扫描线算法对任意复杂轮廓进行分割及转化,建立了数学模型;②提出的基于PSO算法的分解算法能够高效地对模型进行求解,并作为子模块嵌入三阶段排车方法中,从而实现对大型城市地下车库的自动排布;③所提出的模型可单独作为一个功能模块,结合可视化和人机交互功能,辅助设计师快速修改设计方案,大大提高了设计师的工作效率.
附录:模型参数生成算法
算法1 区域车道内轮廓图形分割算法
输入:区域车道内轮廓端点集合{(aw, dw)}w∈ZW
输出:每2条扫描线之间的子区域上下边界线斜率kij, kij及截距bij, bij,每条扫描线对应的纵坐标区间上下边界vij, vij, i∈In, j∈Jm, Jm={1, 2, …, m}
1使用模块1得到扫描线的横坐标集合U={ui}i∈In+1
2 G←Ø,h←0
3 For w=1 to W-1 do
4 For i=1 to n do
5 If aw≤ui < ui+1≤aw+1 or aw+1≤ui < ui+1≤aw
6 h←h+1
7 使用模块2获取端点集合{gh1, gh2, gh3, gh4}
8 G←G∪{gh1, gh2, gh3, gh4}
9 End If
10 End For
11 End For
12 使用模块3获取矩阵G′={g′ij}i∈H, j∈F, H={1, 2, …, h}, F={1, 2, 3, 4}
13计算矩阵G′第1列中重复最多的元素的数量m
14 m←m/2
15初始化kij, kij,bij, bij, vij, vij, i∈In, j∈Jm所有值为0
16 c←0, j←1
17 For i=1 to h/2 do
18 找到g′(2i-1)1在U中对应的元素序号i*
19 如果c=i*,j←j+1;否则,c←i*,j←1
20 使用模块4计算当前区域上下边界线截距和斜率
21 End For
22使用模块5计算每条扫描线对应的纵坐标区间
模块1 对端点横坐标集合{aw}w∈ZW升序排序并去除重复项,得到横坐标集合U={ui}i∈In+1.
模块2 计算第h条线段左右端点横纵坐标值.其中:(gh1, gh2)为线段左端点,(gh3, gh4)为线段右端点. gh1←ui,gh2←(dw+1-dw)(ui-aw)/(aw+1- aw)+dw gh3←ui+1,gh4←(dw+1-dw)(ui+1-aw)/(aw+1-aw)+dw
模块3 对由区域车道内轮廓线段左右端点横纵坐标构成的矩阵G={gij}i∈H, j∈F,以第1列为主要关键字、第2列为次要关键字、第4列为第三关键字按行升序排序,得到G′={g′ij}i∈H, j∈F.
模块4 以G′中的第2i及2i-1条线段为上下边界线,对应扫描线为左右边界线,构成了一个凸多边形.计算其上下边界线斜率及截距如下:
| $ \begin{align} & {{{\bar{k}}}_{i*j}}\leftarrow \frac{g_{(2i)4}^{\prime }-g_{(2i)2}^{\prime }}{g_{(2i)3}^{\prime }-g_{(2i)1}^{\prime }},{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k}{{}_{i*j}}}\leftarrow \frac{g_{(2i-1)4}^{\prime }-g_{(2i-1)2}^{\prime }}{g_{(2i-1)3}^{\prime }-g_{(2i-1)1}^{\prime }} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{{\bar{b}}}_{i*j}}\leftarrow \frac{g_{(2i)3}^{\prime }g_{(2i)2}^{\prime }-g_{(2i)4}^{\prime }g_{(2i)1}^{\prime }}{g_{(2i)3}^{\prime }-g_{(2i)1}^{\prime }} \\ &\ \ \ \ \ \ \ \ \ \ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}{{}_{i*j}}}\leftarrow \frac{g_{(2i-1)3}^{\prime }g_{(2i-1)2}^{\prime }-g_{(2i-1)4}^{\prime }g_{(2i)-11}^{\prime }}{g_{(2i-1)3}^{\prime }-g_{(2i-1)1}^{\prime }} \\ \end{align} $ |
模块5 计算每条扫描线x=ui,i∈In+1与车道内轮廓的交点纵坐标并升序排序,得到集合Ci={cij}j∈Jm′, i∈In+1, Jm′={1, 2, …, m′},m′为交点纵坐标数.初始化空集Vi.将所有端点横坐标为ui、纵坐标分别为cij、ci(j+1),且在车道内轮廓内的线段对应的纵坐标区间[cij, ci(j+1)]加入集合Vi,其中j∈Jm′-1.化简Vi中首尾相接的区间,得到集合V′i.依次将V′i中对应的纵坐标区间上下边界赋值给vij和vij, j∈Jm.
算法2 有序区间求交算法
输入:任意2个有序区间集合
| $ \begin{array}{*{35}{l}} {{A}_{1}}=\bigcup\limits_{j\in {{J}_{{{m}_{1}}}}}{\{z|\lambda _{2j-1}^{1}\le z\le \lambda _{2j}^{1}\}} \\ {{A}_{2}}=\bigcup\limits_{j\in {{J}_{{{m}_{1}}}}}{\{z|\lambda _{2j-1}^{2}\le z\le \lambda _{2j}^{2}\}} \\ \end{array} $ |
输出:有序区间集合A=A1∩A2
1 A←Ø, f1←1, f2←1, j1←1, j2←1
2 While(j1≤2m1 and j2≤2m2)
3 If (λ1j1≤λ2j2)
4 If f1==1 and f2==0), A←A∪{z|λ1j1≤z≤min(λ1j1+1, λ2j2)}
5 j1←j1+1, f1←1-f1
6 Else
7 If f1==0 and f2==1), A←A∪{z|λ2j2≤z≤min(λ2j2+1, λ1j1)}
8 j2←j2+1, f2←1-f2
9 End If
10 End While
| [1] |
许明才. 大城市商圈地区停车规划策略研究——基于上海市三个商业中心停车调查的实证研究[J]. 上海城市规划, 2014(2): 43-50. Xu Mingcai. Study on parking planning strategy of metropolises' commercial center:an empirical study based on parking survey of three business center in Shanghai[J]. Shanghai Urban Planning Review, 2014(2): 43-50. |
| [2] |
谭忠盛, 王梦恕, 王永红, 等. 我国城市地下停车场发展现状及修建技术研究[J]. 中国工程科学, 2017, 19(6): 100-110. Tan Zhongsheng, Wang Mengshu, Wang Yonghong, et al. Present situation and application of urban underground garage[J]. Engineering Science, 2017, 19(6): 100-110. |
| [3] |
陈歌.城市地下公共车库的停车方式与空间设计研究[D].西安: 西安建筑科技大学, 2016.
|
| [4] |
Abdelfatah A S, Taha M A. Parking capacity optimization using linear programming[J]. Journal of Traffic and Logistics Engineering, 2014, 2(3): 176-181. |
| [5] |
Kong Y, Le Vine S, Liu X B. Capacity impacts and optimal geometry of automated cars' surface parking facilities[J]. Journal of Advanced Transportation, 2018, 1-13. |
| [6] |
Huang Junhao, Liao Tianchi, Kang Haining, et al. A general algorithm for rectangular parking optimization design[J]. Journal of Physics Conference Series, 2020, 1486: 032029. DOI:10.1088/1742-6596/1486/3/032029 |
| [7] |
Syahrini I, Sundari T, Iskandar T, et al. Mathematical model of parking space unit for triangular parking area[C]//4th International Conference on Operational Research. Lishon: IOP Publishing Ltd, 2018: 012012.
|
| [8] |
Ihda Hasbiyati, Widiawati Putri, Arisman Adnan, et al. Parking lot optimization in parallelogram using the concept area of rectangular and right triangle[J]. Pure and Applied Mathematics Journal, 2019, 8(4): 77-82. DOI:10.11648/j.pamj.20190804.12 |
| [9] |
Ferreira M, Damas L, Conceiçao H, et al. Self-automated parking lots for autonomous vehicles based on vehicular Ad hoc networking[C]//IEEE Intelligent Vehicles Symposium. Dearborn: IEEE, 2014: 472-479.
|
| [10] |
Timpner J, Friedrichs S, Van Balen J. k-stacks: high-density valet parking for automated vehicles[C]//Intelligent Vehicles Symposium. Seoul: IEEE, 2015: 895-900.
|
| [11] |
Banzhaf H, Quedenfeld F, Nienhuser D. High density valet parking using k-deques in driveways[C]//Intelligent Vehicles Symposium. Redondo Beach: IEEE, 2017: 1413-1420.
|
| [12] |
Nourinejad M, Bahrami S, Roorda M J. Designing parking facilities for autonomous vehicles[J]. Transportation Research Part B Methodological, 2018, 109: 110-127. DOI:10.1016/j.trb.2017.12.017 |
| [13] |
徐涵喆, 黄逸彬, 杨赫, 等. 基于规则的城市地下车库外圈车位排布启发式算法[J]. 北京邮电大学学报, 2019, 42(4): 102-108. Xu Hanzhe, Huang Yibin, Yang He, et al. Rule-based heuristic algorithm for parking spaces allocation in marginal area of urban underground parking lots[J]. Journal of Beijing University of Posts and Telecommunications, 2019, 42(4): 102-108. |
| [14] |
Franzblau D S. Performance guarantees on a sweep-line heuristic for covering rectilinear polygons with rectangles[J]. SIAM Journal on Discrete Mathematics, 1989, 2(3): 307-321. DOI:10.1137/0402027 |
| [15] |
McKenney M, Frye R, Dellamano M, et al. Multi-core parallelism for plane sweep algorithms as a foundation for GIS operations[J]. GeoInformatica, 2017, 21(1): 151-174. DOI:10.1007/s10707-016-0277-7 |
| [16] |
Deng Yong, Liu Yang, Zhou Deyun. An improved genetic algorithm with initial population strategy for symmetric TSP[J]. Mathematical Problems in Engineering, 2015(3): 1-6. |
| [17] |
Ali R, Mounir G, Moncef T. Adaptive probabilities of crossover and mutation in genetic algorithm for solving stochastic vehicle routing problem[J]. International Journal of Advanced Intelligence Paradigms, 2016, 8(3): 318. DOI:10.1504/IJAIP.2016.077498 |
| [18] |
Marini F, Walczak B. Particle swarm optimization(PSO) (A tutorial)[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 153-165. DOI:10.1016/j.chemolab.2015.08.020 |
| [19] |
Zhan Zhihui, Zhang Jun, Li Yun, et al. Adaptive particle swarm optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), 2009, 39(6): 1362-1381. DOI:10.1109/TSMCB.2009.2015956 |



