2. 数学工程与先进计算国家重点实验室 网络密码研究室, 郑州 450002;
3. 解放军信息工程大学 网络空间安全学院, 郑州 450002;
4. 郑州大学 网络管理中心, 郑州 450001
低速拒绝服务攻击对于域间路由系统造成威胁,已有失效恢复算法未能有效解决恢复拓扑计算的时间复杂度高和节点聚合控制等问题,为此,提出一种基于度约束最小生成树的失效恢复算法.通过设计基础迁移子算法和复杂迁移子算法,在满足度约束的条件下根据遭袭路由系统生存拓扑构建新的恢复拓扑,并针对上述两类迁移子算法,分别提出关键点选择子算法,用于判定和计算迁移过程所需的关键节点.理论分析和仿真实验结果证明,该算法生成的恢复拓扑在有效控制节点度的同时,具有较优的性能.
2. Network Cryptography Laboratory, State Key Laboratory of Mathematical Engineering and Advanced Computing, Zhengzhou 450002, China;
3. School of Cyberspace Security, PLA Information Engineering University, Zhengzhou 450002, China;
4. Network Management Center, Zhengzhou University, Zhengzhou 450001, China
In view of the threat of low-rate denial of service attacks on inter-domain routing system, the existing failure recovery methods fail to solve problems including high time complexity and node aggregation control. A failure-recovery algorithm based on degree-constrained minimum spanning tree named degree-constrained minimum spanning tree based failure recovery (DR) is proposed. By designing the Fundamental Transfer sub-algorithm and the complex transfer sub-algorithm, a new recovery topology can be constructed according to the survival topology of the attacked routing system under the condition of given degree constraint. For the above two types of transfer sub-algorithms, two selection sub-algorithms are respectively advanced for the determination and calculation of key nodes. Theoretical analysis and simulation experiments verify that the recovery topology generated by DR has better performance while effectively controlling the node degree.
近年来,域间路由系统面临的安全防护压力逐步加大[1-3],边界网关协议低速拒绝服务(BGP-LDoS,border gateway protocol-low-rate denial of service)攻击的攻击威胁与复杂程度不断攀升[4]. Schuchar和Kan的实验结果均证明,BGP-LDoS攻击能够导致域间路由系统局部乃至整体失效.伴随物联网的发展,以大规模僵尸网络为基础攻击条件的BGP-LDoS将给域间路由系统带来更为深远的影响.
域间路由系统失效恢复,旨在利用多种路由恢复技术保障网络遭袭后生存节点的通信.按照失效自治域和域间链路的数量,可将已有路由失效恢复算法划分为基于单链/单域失效的路由恢复和基于多链/多域失效的路由恢复.前者以路径拼接[5]和混合抗干扰方法[6]为代表,难以应对BGP-LDoS攻击造成的多点无关联区域失效场景.后者指无邻接关系的多个自治域区域近乎同时并发呈现通信中断态势下,针对尚存活自治域实施报文转发路径的动态切换,以IP快速重路由[7]和多级可信传输机制(CETML,credible transmission with multiple levels)[8]为代表.此类算法在预计算备份子图生成方面存在时间复杂度较高的问题,且BGP-LDoS攻击以高度聚合的中心节点为攻击目标,已有CETML等算法未考虑对生成子图中节点度的控制,因此在面对BGP-LDoS攻击时其生成的备份子图大都具有高中心度节点特性,导致其二次抗毁性较差.
综上,借鉴中心化网络控制的设计理念,通过定义BGP-LDoS袭击域间路由系统后生存路由的规划,提出一种基于度约束最小生成树的路由失效恢复算法(DR,degree-constrained minimum spanning tree based failure recovery).笔者的主要贡献为:①基于DR算法实现的域间路由失效恢复方案,在产生最小生成树,即路由系统恢复拓扑的过程中能够有效控制节点的聚合,避免生成具有过高度数节点;②针对已有多链/多域恢复算法在备份子图生成方面存在时间耗费较高的问题,DR算法能够有效降低恢复路由的生成时长.
1 域间路由系统路由失效恢复针对自治域(AS,autonomous system)和域间路由系统拓扑开展研究.应用互联网数据分析中心(CAIDA,center for applied internet data analysis)[9]针对来自多个数据源的AS级拓扑特性的统计表明,平均度值的范围基本落于[4, 6],数据源中的最大度值范围为[2 607,4 386].由CAIDA基于ARK(Archipelago)和基于traceroute的计算节点度值的统计可知,度值大于10的节点概率均为0.09左右,大于1 000的节点概率约为0.005,表明大多数节点的度值小于10.
1.1 度约束最小生成树度约束最小生成树(DCMST,degree-constrained minimum spanning tree),即如果针对最小生成树中各顶点的度数加上一定的数目限制,则满足条件的最小生成树记为度约束最小生成树.对于连通图G=(V, E),其节点集合V={v1, v2, …, vn},节点个数为|V|;边的集合E={e1, e2, …, ek},边的个数为k;每条边对应的权值为wij;假定T表示G中所有满足度约束的生成树集合.
1.2 生成树编码针对域间路由系统中面对的BGP-LDoS攻击,提出一种节点表示法(NR,node representation),便于图中节点编码.对于一个简单无向图G=(V, E),存在一个生成森林F=(V, EF)是G的无环子图,F中的一棵树T=(VT, ET)是F中的一个连接部分,有VT⊆V.对于一个图G及其中一棵树T,GT=(VGT, EGT)是由节点集合VT生成的一个子图,即EGT包含的所有边(x, y)∈E,均满足x∈VT和y∈VT.
对于一棵树T,根为Root,定义节点n的进深为从n到Root的路径长度,记为p(n). NG(n)表示G中毗邻节点n的节点集合. G中一个节点的度表示为dG(x),T中一个节点的度表示为dT(x). G中一棵树T的度记为dG(T),是指对于G的边集E,射入属于VT集合节点的边的总数.与之类似,T中边的个数为dT(T)=|VT|-1.
一棵树T的NR为一个有序列表,其中每个NR涵盖4个元素(n,I,p,d):分别表示节点、索引、节点进深和节点度值.对于一个节点n,I(n)表示其索引值,p(n)和dG(n)分别表示其进深和度值.对于T,考虑到深度优先搜索对于节点的顺序特性,基于深度优先法则实施NR编码时,搜寻到一个未访问过的节点,则可将该节点以及对应的进深、度值加入NR编码序列.
一棵生成树F的NR编码,记为森林表示(FoR,forest representation),是F中每棵树T的NR合并.由于一片森林包含多棵树,则可用一个对偶(hT,dT)表示一棵树,前者表示指向树T的指针,后者表示该树的度值.
1.3 DR算法建立1) 对于代表多个自治域组成的域间路由系统,其对应原始图G.在应对路由失效而生成DCMST时,由于域间路由节点在不断迁移和变化,因此通过创建并逐步完善编码矩阵的方式记录该过程.
子算法1 节点迁移编码TransferNodesEncode()
输入:图G(代表多个自治域组成的域间路由系统). 输出:节点的迁移编码矩阵MN.
① 对于G中一棵树Fi中的某节点n,创建其对应的组数An=[i, Hi, I(n)i],i表示该节点所属树的序号,Hi为指向树Fi对应NR编码的指针,最后的I(n)i为NR中n对应的索引值;②假设F1是来自G的首个森林,在F1的基础上,随着节点或子树的裁剪和迁移,不断生成的森林序列记为L=[F1,F2,…,Fi];③若节点n所在的一棵子树SubTr,从树Fj迁移至树Fk,则节点n将被重新定位,该节点的迁移编码矩阵记为Mn=[A1T, …, AjT, AkT].
2) DR算法通过定义FundamentalTransfer(FT)和ComplexTransfer(CT)以产生新的生成森林,即从已有生成森林F对应的森林表示FoR,产出新生成森林F′的FoR. FT和CT操作的目标是从森林中的Torigin(一组树)里的子树迁移至另一棵树Tdst.
子算法2 基础迁移FundamentalTransfer(),FTFT针对BGP-LDoS攻击后,导致域间路由系统中某一关键节点失效的典型场景,针对该问题构建新的森林,并有效满足度约束值.
输入:森林F的FoR序列中树Torigin和Tdst的索引;被迁移子树Torigin中的根r,此时也称之为修剪节点;新树Tdst中的节点t,t满足在图G中与r相邻;度约束值c. 输出:新生成森林F′的FoR.
① 寻找Torigin中修剪节点r所属子树,其对应的索引范围是[I(r),I(m)],该范围涵盖了节点r及其后继节点m等,且满足p(r)值小于后继节点.考虑到I(r)值已知,通过顺序搜索可发现后继节点的I(m);②临时创建一个中间树Tmid,用于存放迁移过程中的节点及子树;③将Torigin中索引范围[I(r),I(m)]内的NR编码放入临时Tmid,按照p(n)-p(r)+p(t)+1计算Tmid每个n的I(n);④创建一个序列T′dst,包含Tdst和Tmid所有节点.通过生成一棵新树,将以r为根的子树迁移至T′dst.仅当满足d(t)<c+1时,将Tmid插入T′dst的[I(t)+1]索引处,之后修正p(t)=p(t)+1;若不满足则跳转到步骤④,对t之后的下一节点进行判断;如果t已是Tdst中最后节点,则表明c过小,FT结束;⑤创建序列T′origin,包含排除Tmid所含节点以外Torigin中的所有节点,之后修正Torigin中d(r)=d(r)-1;⑥复制F对应的NR,生成一个新的F′.将指向F′中新旧两棵树的指针分别记为h_T′origin和h_T′dst;⑦计算dG(T′origin)和dG(T′dst),并存储于F′;⑧对矩阵MN中T′origin和T′dst的每个节点n修正.
子算法3 复杂迁移ComplexTransfer(),CT
针对域间路由系统在遭受BGP-LDoS攻击后,导致毗邻的多个自治域节点失效场景,设计CT子算法生成度约束最小生成树,予以实施路由恢复.
输入:森林F的FoR序列中树Torigin和Tdst的索引;被迁移树Torigin中的根r;修剪节点f;新树Tdst中的节点t,t满足在图G中与r相邻;度约束值c. 输出:新生成森林F′的FoR.
① 寻找Torigin中根节点r所属子树,其对应索引范围[I(r),I(m)],该范围涵盖节点r及其后继节点m等,且满足p(r)值小于后继节点;②临时创建2个中间树Tmid1和Tmid2,用于存放迁移过程中的节点及子树;③将Torigin中索引范围[I(r),I(m)]内的NR编码,放入临时Tmid1,按照p(x)-p(r)+p(t)+1计算Tmid1每个节点n的I(n);④ Torigin中从r到f的路径中节点,标记为[r1,r2, …,rn],对应于r=r1,以及f=rn;⑤寻找从r到f的路径.初始化Tmid2为空NR,对于每个i(1<i≤n),仅当满足d(i)<c+1时,复制以ri为根的子树(但不包括以ri-1为根的子树)到Tmid2的末端,同时,按照p(n)-p(r)+i+p(t)+1方式修正每个加入Tmid2的节点n的进深值;之外,执行p(r)=p(r)+1和p(f)=p(f)-1以修正节点r和f;若不满足d(i)<c+1,在跳转至步骤⑤,对下一个节点ri+1判断;如果ri已是Tdst中最后节点,则表明c过小,CT结束;⑥将被裁剪子树和Tdst连接组合成新树T′dst,即包含Tdst,Tmid1和Tmid2,以[Tmid1Tmid2]序列方式置于T′dst的(t+1)处,执行d(t)=d(t)+1修正t的度值;⑦利用Torigin中[Ttmp1Ttmp2]之外的节点创建T′origin,将原Torigin中f的前趋节点度值减1;⑧复制F对应的NR生成一个新的森林F′,将指向F′中新旧两棵树的指针分别记为h_T′origin和h_T′dst;计算dG(T′origin)和dG(T′dst)并存于F′;⑨修正矩阵MN中T′origin和T′dst中的每个节点n.
子算法4 单树森林修正算法UpdateForSingleTree()
上述算法在应用CT与FT时,均假设一个森林中至少存在两棵树.为了扩展算法的适用性,可将仅有一棵树的森林予以修正,依照特殊方式实施操作.
输入:森林F的唯一树Torigin. 输出:新生成森林F′的FoR.
① 建立一棵树Tsup进行辅助,假设该树仅包含一个节点n,此时该节点n∉G,且n与Torigin中每个节点均保持连接;②令Tdst为Tsup,执行FT,由此可将Torigin中一棵子树变为Tsup中n的后继;③利用FT或CT操作,将以n为根子树变为原始树,从而生成一个新的森林F′.
子算法5 FT关键节点选择KeyNodeSelectionForFT()
输入:森林F的FoR序列. 输出:FT中新树Tdst中节点t,被迁移子树Torigin中的根r.
① 随机寻找F中一棵树T,需满足dG(T)大于dT(T),令Torigin为T.若无法找到,则说明图G本身即单个森林,停止该过程;②从Torigin中随机确定一个非根节点r,dG(r)大于dT(r);③从NG(r)随机选择一个节点n,若边(n,r)不属于ET,则令t为n,否则跳过本步骤;之后通过搜寻矩阵以确定节点t在森林F中的索引I(t);④若t属于Torigin的节点集合,则执行单树森林操作;否则执行FT.
子算法6 CT关键节点选择KeyNodeSelectionForCT()
输入:森林F的FoR序列. 输出:被迁移树Torigin中的根r;修剪节点f;新树Tdst中的节点t.
① 随机寻找F中一棵树T,需满足dG(T)大于dT(T),令Torigin为T.若无法找到,则说明图G本身即单个森林,停止该过程;②从Torigin中随机确定一个非根节点r,dG(r)大于dT(r);③寻找r至Torigin根的路径,令i为1且ri为r,以向根的方向从Torigin中I(r)开始遍历,步长为1,同时判别遍历过程中的每个节点n,若p(n)小于p(ri),则令ri+1为n.若i>2,则在[2, …, i-1]范围内随机选择j,令f为rj;若整个路径仅包含节点r和根,则令f为r;④从NG(r)中随机选择一个节点n,若边(n, f)不属于ET,则令t为n,否则重复本步骤;之后,通过搜寻矩阵以确定节点t在森林F中的索引I(t);⑤若t属于Torigin的节点集合,则执行单树森林操作;否则执行FT.
1.4 基于DR算法的恢复路由生成流程首先,基于节点表示法NR,对由多个AS组成的路由系统编码,将系统表示为含有多棵树的森林,记为FoR;其次,如果目前FoR代表仅含单树的森林,由于后续的基础迁移FT和复杂迁移CT算法均假设森林中至少存在两棵树,因此为拓展算法的适用性,利用单树森林修正算法UpdateForSingleTree()对该森林修正.反之,则直接进行失效AS节点迁移操作;再次,路由系统遭袭后通常会造成单个失效自治域节点或多个毗邻失效自治域节点,根据2种不同的情况,分别采用FT关键节点选择算法和CT关键节点选择算法,率先计算出2种情况下的关键节点;之后,分别利用FT算法和CT算法,实施失效节点的迁移操作,完成域间路由系统恢复.
2 时间复杂度分析分析度约束最小生成树的时间复杂度.对于多域社团抽象出的连通图G,包含的自治域数目为n.
定义1 s=|Torigin|+|Tdst|,其中|Torigin|和|Tdst|分别表示参与节点交换的两棵树的容量大小,s即代表交换操作的时间复杂度,其平均值为s.
定义2 t=|T|表示G中生成森林中树的个数.
定义3 sop=sFT+sCT,表示FT和CT操作的时间复杂度,其平均值为sop.
定义4 sinit为初始化子树指针h、新树根rnew、备选节点序列等参数的复杂度,其平均值为sinit.
度约束最小生成树的时间复杂度C=sop+sinit.
1) 计算s.如果连通图G中的n个节点均匀分布于t棵树(假定
| $ \overline s = \sum\limits_{|i, j| \in K} {\frac{{|{T_i}| + |{T_j}|}}{{|K|}}} $ |
其中,若固定i不变,则对于|Ti|+|Tj|有t-1组,此时|Ti|+|Tj|之和为
| $ \left( {t - 1} \right)|{T_i}| + \sum\limits_j {|{T_j}| - |{T_i}|} $ |
之后对每种Ti情形累加,求和可得
| $ \overline s = \sum\limits_{\left\{ {i, j} \right\} \in K} {\frac{{|{T_i}| + |{T_j}|}}{{|K|}} = \frac{{2n}}{t} = O\left( {\frac{n}{t}} \right) = O\left( {\sqrt n } \right)} $ |
2) 计算sop.根据FT和CT操作步骤,可知
| $ {s_{{\rm{op}}}} = O\left( {|{T_{{\rm{origin}}}}| + |{T_{{\rm{dst}}}}| + t} \right) = O\left( {s + t} \right) $ |
由上述1)结论,则有
| $ {\overline s _{{\rm{op}}}} = O\left( {\overline s + \overline t } \right) = O\left( {\sqrt n } \right) $ |
3) 计算sinit.根据初始化过程可知
| $ {\overline s _{{\rm{init}}}} = O\left( t \right) + O\left( {3|{T_{{\rm{init}}}}|} \right) + O\left( {\overline s + \frac{n}{s}} \right) $ |
|Tinit|的上限为|Torigin|+|Tdst|,则由1)、2)可知
| $ \begin{array}{c} O\left( {3|{T_{{\rm{init}}}}|} \right) = O\left( {s + t} \right)\\ {\overline s _{{\rm{init}}}} = O\left( {\overline s + t + \frac{n}{{\overline s }}} \right) = O\left( {\sqrt n } \right) \end{array} $ |
4) 度约束最小生成树的时间复杂度C
| $ \overline C = {\overline s _{{\rm{op}}}} + {\overline s _{{\rm{init}}}} = O\left( {\sqrt n } \right) $ |
分析可知,度约束最小生成树的平均时间复杂度为
利用锦标赛选择法挑选子代,操作数选择为2,分别对应FT操作和CT操作.基于精英选择策略,通过对收敛速度的判别,确保仅有最佳解决方案被用于构建下一代生成树.
3.1 基于随机图的仿真利用拓扑产生器,基于广义线性优先(GLP,generalized linear preference)模型生成随机图,代表路由系统AS级拓扑.设置随机图节点个数分别为10、50、100、200、400、600、800、1 000.模拟BGP-LDoS对上述随机图实施袭击,针对存活节点及链路,分别利用DR算法同边集表示(ESR,edge set representation)[10]、基于蚁群的度约束生成树(AB-DCST,ant-based algorithm for degree constrained spanning trees)[11]和混合稳定态遗传算法(HSSGA,hybrid approach combining a steady-state genetic algorithm)[12]3种算法生成DCMST.对生成树节点度值范围限定在[3,6];GLP生成的随机图平均节点度为4.1.
1) DR与ESR算法对比
ESR利用特定交换和变异,由边集操作产生新树.仿真实验同样采用文献[10]中对ESR的设置,交换概率和变异概率均为0.8.
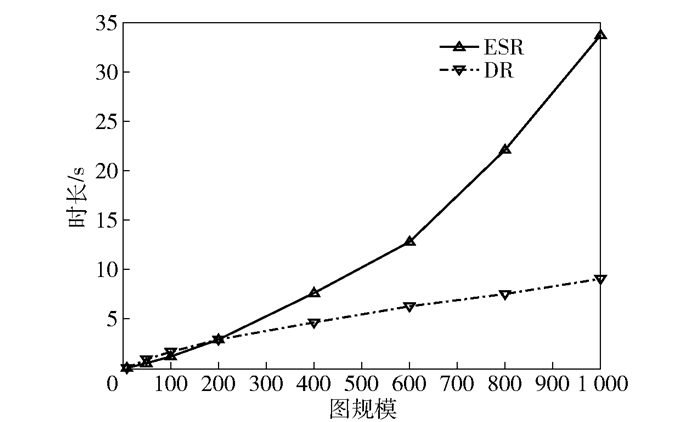
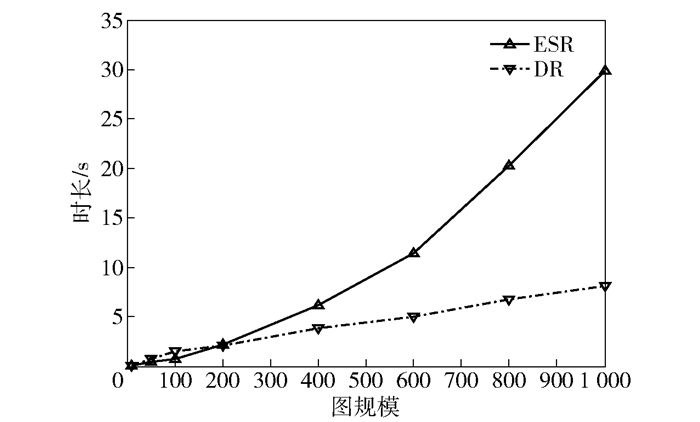
图 1和图 2分别给出了在限制度值分别为3和6的情况下,包含不同节点个数的随机图,利用ESR算法和DR算法分别生成DCMST所花费时间的对比.由图可知,2种算法下,随着度值约束的放松,即在约束值越高的情况下,随机图生成时间相对越短.整体上,同样拓扑规模对应的DCMST生成时间差距较小.
|
图 1 限定度约束为3的不同图规模下DCMST生成时间 |
|
图 2 限定度约束为6的不同图规模下DCMST生成时间 |
DR算法相对于ESR算法具有明显的性能优势,伴随着拓扑规模增大,性能优势越发突出.与时间复杂度理论分析相比,DR算法在随机图仿真条件下性能表现更好,优于平均时间复杂度.
2) DR与AB-DCST算法对比
AB-DCST算法模拟蚁群在图中移动,识别候选边集,从而建立度约束最小生成树. 表 1中|V|代表节点个数,生成所用时长均以s为单位,可知随着度约束值的逐步增大,DR与AB-DCST算法生成度约束最小生成树的时间均在减少.在具备同样度约束值的情况下,对于相同节点个数的随机图,DR算法的生成速度要快于AB-DCST算法.
|
|
表 1 DR与AB-DCST算法性能比较 |
值得注意的是,随着图中节点个数的增加,DR算法相比于AB-DCST算法的性能优势相对在扩大;其他度约束值情况下,也具有相似特征,表明DR算法在面对大规模随机图时,具有更好的生成效率.
3) DR与HSSGA算法对比
HSSGA为混合式的构建算法. 表 2所示为DR与HSSGA在度约束为3、4、5情况下的消耗时间.
|
|
表 2 DR与HSSGA算法性能比较 |
由表 2可知,伴随度约束的宽松,2种算法下生成DCMST的时长都在逐步减少.对于相同节点个数和相同度约束,比较二者消耗时长,发现DR算法优于HSSGA算法.此外,需要注意的是,在相同度约束下,随着节点数的增大,DR算法相比于HSSGA算法的性能优势在逐步降低.
3.2 基于CAIDA的仿真利用来自CAIDA的真实互联网拓扑对DR算法进行仿真,分别从名为BGP_tables和WHOIS的数据集获得样本拓扑,从2个原始数据集中抽取涵盖前3 000个AS节点的拓扑进行仿真.将取自BGP_tables的局部拓扑命名为B_tpl,平均度值为2.51;将取自WHOIS的局部拓扑命名为W_tpl,平均度值为6.53.
模拟BGP-LDoS对B_tpl和W_tpl拓扑实施攻击,针对存活节点及链路,分别利用DR算法同ESR、AB-DCST和HSSGA算法生成DCMST,作为域间路由系统遭袭后的恢复拓扑,对生成树节点度值范围也限定为[3,6].
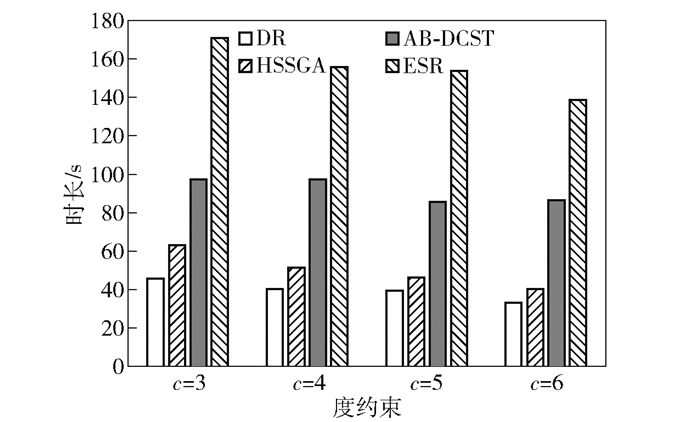
图 3给出了B_tpl样本下,度约束范围在[3,6]内使用DR算法和其他3种算法生成DCMST的时间对比.可知,4种算法下,随着度值约束的放松,DCMST的生成时间整体上均逐步缩减;虽然DR在度约束5和度约束4情形下时间损耗基本持平,但整体趋势仍为缩减.相比于ESR、AB-DCST和HSSGA算法,DR算法具有相对一定的优势,有效降低了DCMST生成时间.
|
图 3 B_tpl样本不同度约束条件下DCMST生成时间对比 |
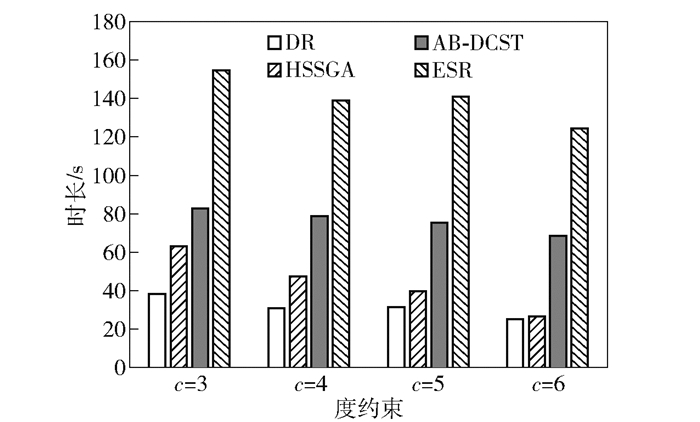
图 4所示为W_tpl样本下,度约束范围在[3,6]内使用4种算法生成DCMST的时间比较.同B_tpl样本仿真结果类似,一方面,随着度值约束条件的放松,DCMST的生成时间也在逐步缩减;另一方面,DR算法对比ESR和AB-DCST算法整体具有显著的性能优势;此外,DR相对于HSSGA算法,在度约束值为[3,5]区间内也有较优表现,在度约束为6时,二者差异较小.
|
图 4 W_tpl样本不同度约束条件下DCMST生成时间对比 |
基于DCMST的域间路由恢复算法DR,在降低生成恢复拓扑时间复杂度的同时,有效控制节点聚合问题.为记录拓扑生成时的节点迁移信息,设计了子算法TransferNodesEncode();为从已有生成森林产出新的生成森林,设计了子算法FundamentalTransfer()/ComplexTransfer();为了判定和计算迁移过程中的关键节点,分别提出KeyNodeSelectionForFT()/KeyNodeSelectionForCT().理论分析结果表明,DR计算DCMST的平均时间复杂度为
| [1] |
Sermpezis P, Kotronis V, Dainotti A, et al. A survey among network operators on BGP prefix hijacking[J]. ACM SIGCOMM Computer Communication Review, 2018, 48(1): 64-69. DOI:10.1145/3211852.3211862 |
| [2] |
Florian S, Franziska L, Robert B, et al. BGP communities: even more worms in the routing can[C]//Internet Measurement Conference. Boston: ACM Press, 2018: 279-292. https://www.researchgate.net/publication/334080715_BGP_Communities_Even_more_Worms_in_the_Routing_Can
|
| [3] |
Brivaldo J, Ronaldo A F, Italo C, et al. High-fidelity interdomain routing experiments[C]//ACM SIGCOMM Conference on Posters and Demos. Budapest: ACM Press, 2018: 36-38. https://dl.acm.org/doi/abs/10.1145/3234200.3241324
|
| [4] |
Li Heshuai, Zhu Junhu, Wang Qingxian, et al. LAAEM:a method to enhance LDoS attack[J]. IEEE Communications Letters, 2016, 20(4): 708-711. DOI:10.1109/LCOMM.2016.2532330 |
| [5] |
Motivala M, Elmore M, Feamster N, et al. Path splicing[J]. ACM SIGCOMM Computer Communication Review, 2008, 38(4): 27-38. DOI:10.1145/1402946.1402963 |
| [6] |
孙子文, 张炎棋, 徐宜敏. 一种采用混合抗干扰方法的路由恢复机制[J]. 系统仿真学报, 2019, 32(5): 874-884. Sun Ziwen, Zhang Yanqi, Xu Yimin. A route recovery mechanism using hybrid anti-interference method[J]. Journal of System Simulation, 2019, 32(5): 874-884. |
| [7] |
Gopalan A, Ramasubramanian S. IP fast rerouting and disjoint multipath routing with three edge-independent spanning trees[J]. IEEE/ACM Transactions on Networking, 2016, 24(3): 1336-1349. DOI:10.1109/TNET.2015.2440179 |
| [8] |
陈文龙, 赵一荣, 肖融, 等. 基于虚拟拓扑的多级可信传输体系及路由计算[J]. 计算机研究与发展, 2018, 55(4): 729-737. Chen Wenlong, Zhao Yirong, Xiao Rong, et al. Packets transmission with multiple levels of credibility and routing calculation based on virtual topologies[J]. Journal of Computer Research and Development, 2018, 55(4): 729-737. |
| [9] |
CAIDA. CAIDA's internet topology data comparison[EB/OL]. 2012(2012-05-15)[2019-08-26]. http://www.caida.org/research/topology/topo_comparison.
|
| [10] |
Raidl G R. Edge sets:an effective evolutionary coding of spanning trees[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(3): 225-239. DOI:10.1109/TEVC.2002.807275 |
| [11] |
Thang N B, Xianghua D, Catherine M Z. An improved ant-based algorithm for the degree-constrained minimum spanning tree problem[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(2): 266-278. DOI:10.1109/TEVC.2011.2125971 |
| [12] |
Singh K, Sundar S. A hybrid genetic algorithm for the degree-constrained minimum spanning tree problem[J]. Soft Computing, 2019, 24: 2169-2186. |


