第5代移动通信系统的3个典型场景是增强移动宽带、大规模机器式通信和超可靠低延迟通信^[1].为了适应这些场景，人们提出了各种新的技术.其中，索引调制(IM, index modulation)^[2]由于其本身具有的高效频谱利用率和高效功率利用率特性引起了人们的极大兴趣. IM不是通过直接改变信号波形来传递信息，而是通过选择不同的索引序号来传递信息.索引资源可以是物理的，例如天线、子载波、时隙、频率载波和扩频码，也可以是虚拟的，例如虚拟并行信道、信号星座、空时矩阵和天线激活顺序.

另外，多址技术是每一代通信系统的关键技术，传统上，可以定义两类多址技术，即正交多址(OMA, orthogonal multiple access)和非正交多址(NOMA, non-orthogonal multiple access)^[3]. NOMA允许多个用户在可用资源上进行并发传输，同时通过控制发射功率(功率域NOMA)^[4]或星座的稀疏编码，即稀疏码多址(SCMA, sparse code multiple access)^[5]来最大程度地减少诱发的干扰.尽管NOMA有了一些改进，但是星座矩阵的复杂设计以及复杂的检测接收机算法阻碍了NOMA的适用性.因此，Mesleh等^[6]提出了索引调制多址接入(IMMA，index modulation multiple access)方案，不仅提高了系统的频谱效率还提高了能量效率.该方案利用IM的优势，以时分多址(TDMA, time division multiple access)中的时隙形式进行操作.然而，IMMA中的每个用户可以单独地选择自己的时隙而不需要任何中央管理或调度，并且时隙可以在2个或更多用户之间共享.通过仿真结果发现，与传统的TDMA和SCMA方案相比，IMMA方案在误码性能上有了明显的提高.最近，在IMMA的基础上，提出了正交索引调制多址接入技术^[7] (QIMMA, quadrature IMMA)，进一步提高了频谱效率和误码率性能.由于QIMMA的最优多用户检测具有较高的计算复杂度，因此，提出了2种基于接收端球形译码的低复杂度检测算法，一种是通过进行深度优先球形译码来减少搜索次数，另外一种通过引入加权因子利用排序算法来增强发射端每种发送时隙组合的检测准确性.这2种低复杂度检测算法在性能达到最优的前提下都能降低1/3以上的复杂度.最后通过仿真结果和理论分析对所提算法进行了验证.

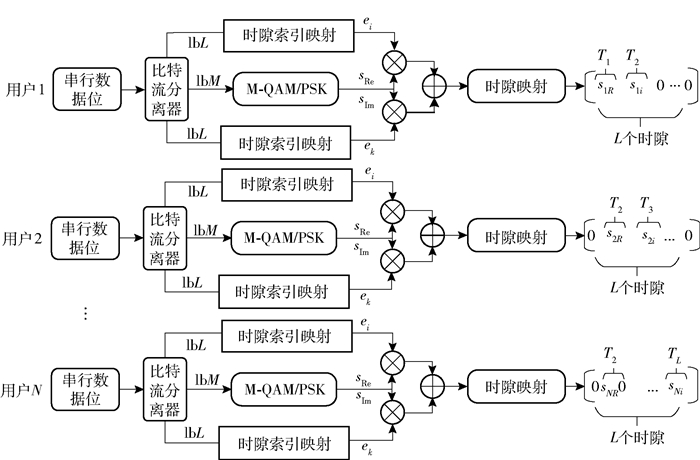
1 正交索引调制多址系统模型

研究了一个由N个用户和一个BS组成的多用户系统, 如图 1所示.上行链路传输的时间帧被划分为L正交时隙.在特定时隙，假设用户和BS之间的信道系数是独立的、同分布的复高斯随机变量，h_ln~CN(0, 1)，1≤n≤N和1≤l≤L，表示在第l个时隙第n个用户和BS之间的信道系数.因此，N个用户与BS之间形成了L×N信道矩阵H.

在所提出的QIMMA方案中，在每个用户的每个时刻发送一个lbML²位块，其中M表示所考虑的是星座图的阶数.输入位被分成3个块：lbM，lbL和lbL；第1块lbM比特流被映射到一个传统的星座符号：s=s_Re+js_Im，比如M-QAM；其余两块lbL和lbL分别用于选择时隙索引向量e_i来传输星座符号的实部s_Re，和时隙索引向量e_k来传输虚部s_Im，其中e_i, e_k∈R^L，i, k∈{1, 2，…, L}，分别表示单位矩阵I_L的第i和k列向量.换句话说, 它们分别用于激活2个时隙来传输所得的星座符号的实部s_Re和虚部s_Im.最后，通过把实部s_Ree_i和虚部s_Ime_k相加，得到一个发射空间向量S：

$ \boldsymbol{S} = {s_{{\rm{Re}}}}{\boldsymbol{e}_i} + {\rm{j}}{s_{{\rm{Im}}}}{\boldsymbol{e}_k} $

(1)

在接收端，在第l个时隙接收到的信号可以表示为

$ {\boldsymbol{y}_l} = \sum\limits_{n = 1}^N {{h_{nl}}{s_{nl}} + {n_l}} $

(2)

其中s_nl是第n个用户在第l个时隙上发送的信号，即s_nl=x_n(l)，x_n表示来自第n个用户的传输矢量. n_l是具有零均值和方差为σ²的加性高斯白噪声.因此，接收的信号向量Y为

$ \boldsymbol{Y} = {\rm{diag}}\left( {\boldsymbol{HX}} \right) + \boldsymbol{N} $

(3)

其中：diag(·)表示对角线算子，且X=[x₁  x₂  …  x_n]^T , N=[n₁  n₂  …  n_L]^T.

在接收端，应用最大似然检测来检测传输矩阵，有

$ \boldsymbol{\hat X} = \arg \;{\min _{\boldsymbol{X} \in \psi }}\parallel \boldsymbol{Y} - {\rm{diag}}\left( {\boldsymbol{HX}} \right)\parallel _{\rm{F}}^2 $

(4)

其中ψ是包含所有可能的传输矩阵的集合，ψ是一个1×(ML²)^N的cell元胞数组，里面的每一个元素是一个N×L的矩阵.‖·‖_F²表示Frobenius范数.

下面给出了所提出的QIMMA方案的示例，假设L=4个时隙和N=4个用户，其中每个用户发送M=4-QAM符号.用户分别由用户1、用户2、用户3和用户4来表示.同样，时隙由T₁、T₂、T₃和T₄表示.对于T₁、T₂、T₃和T₄，每个时隙都有由2 bit指示的唯一索引，分别为00、01、10和11.因此，QIMMA方案中每个用户在每个传输瞬间发送lbML²=6位的比特块.假设所有用户的传输块为{101011, 110110, 011001, 111110}.每个用户将根据其相应块的第1块lbL=2位{10, 11, 01, 11}确定传输符号实部要使用的时隙的索引.每个用户的第2块lbL=2比特{10, 01, 10, 11}将被用于确定传输符号虚部要使用的时隙的索引.每个用户的第3块lbM=2比特{11, 10, 01, 10}将被于调制4QAM符号，根据映射规则得到调制符号，分别表示为s₄、s₃、s₂和s₃.再根据时隙索引的映射规则，最终得到传输矢量可以分别形成为x₁=[0, 0, s_4Re+js_4Im, 0]，x₂=[0, js_3Im, 0, s_3Re]，x₃=[0, s_2Re, js_2Im, 0]，x₄=[0, 0, 0, s_3Re+js_3Im].并且传输矩阵X可以相应地表示如下：

$ \boldsymbol{X} = \left[ {\begin{array}{*{20}{c}} 0&0&{{s_{4{\rm{Re}}}} + {\rm{j}}{s_{{\rm{4Im}}}}}&0\\ 0&{{\rm{j}}{s_{3{\rm{Im}}}}}&0&{{s_{{\rm{3Re}}}}}\\ 0&{{s_{{\rm{2Re}}}}}&{{\rm{j}}{s_{{\rm{2Im}}}}}&0\\ 0&0&0&{{s_{{\rm{3Re}}}} + {\rm{j}}{s_{{\rm{3Im}}}}} \end{array}} \right] $

X矩阵的行代表用户数，列代表时隙数.请注意，在该示例中，T₁未被用于传输任何用户的信息，而T₂同时由用户2和用户3使用，T₃同时由用户1和用户3使用，T₄同时由用户2和用户4使用.因此，2个用户之间都会产生信道间干扰，从而影响误码性能.下面将证明QIMMA方案的性能优于IMMA方案.

2 性能分析 2.1 误码率分析

端到端QIMMA系统的误码率可以通过计算成对错误概率(PEP，pairwise error probability)来表示.假设发送信号是X, 由ML检测得到$ \boldsymbol{\hat X} $，则条件成对错误概率P可以推算为^[6]

$ \begin{array}{c} P\left( {\boldsymbol{X} \to \hat X|\boldsymbol{H}} \right) = \\ P\left( {\parallel \boldsymbol{Y} - {\rm{diag}}\left( {\boldsymbol{HX}} \right)\parallel _{\rm{F}}^2 > \parallel \boldsymbol{Y} - {\rm{diag}}\left( {\boldsymbol{H}\hat X} \right)\parallel _{\rm{F}}^2} \right) = \\ \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {\exp \left( { - \frac{\varphi }{{4{\sigma ^2}{{\sin }^2}\theta }}} \right)} {\rm{d}}\theta \end{array} $

(5)

其中$ \varphi = \parallel {\rm{diag}}\left( {\boldsymbol{H}\left( {\boldsymbol{X} - \hat X} \right)} \right)\parallel _{\rm{F}}^2 $. σ为高斯噪声的方差，一般定义为设$ \phi = \boldsymbol{X} - \boldsymbol{\hat X} $，ϕ_nl是ϕ的第n行，第l列的元素, $ \varphi = \sum\limits_{l = 1}^L {\parallel \sum\limits_{n = 1}^N {{h_{\ln }}{\phi _{nl}}} } \parallel _{\rm{F}}^2 $是L个指数随机变量的累加和，第l个随机变量的均值是$ {\mu _1} = \sum\limits_{n = 1}^N {\parallel {\phi _{nl}}\parallel _{\rm{F}}^2} $.在L个指数随机变量中，有K个均值不为零，其中K≤L.假设存在R个不同的均值记为μ₁, μ₂, …, μ_R，其中R≤K，将拥有同样均值μ_i的个数表示为r_i.因此，有r₁+r₂+…+r_R=K.由文献[6]可知

$ \begin{array}{c} {\rm{P}}\left( {\boldsymbol{X} \to \boldsymbol{\hat X}} \right) = {\sum\limits_{q = 1}^R {\chi _q^{{r_q}}\sum\limits_{\omega = 1}^{{r_q}} A {{\left( { - 1} \right)}^{{r_q} - w}}\left( {\frac{\lambda }{{{\chi _q}}}} \right)} ^\omega } \times \\ \sum\limits_{k = 0}^\omega {\left( {\begin{array}{*{20}{c}} {\omega - 1 + k}\\ k \end{array}} \right)} {\left( {1 - \lambda } \right)^k} \end{array} $

(6)

其中：$ {\chi _x} = \frac{1}{{{\mu _x}}}, \lambda = \frac{1}{2}\left( {1 - \frac{1}{{\sqrt {1 + 4{\sigma ^2}{\chi _q}} }}} \right) $，

$ A = \sum\limits_{\begin{array}{*{20}{c}} {{m_1} + \cdots + {m_R} = {r_q} - w}\\ {{m_{q = 0}}} \end{array}} {\prod\limits_{\begin{array}{*{20}{c}} {{\rm{t}} = 1}\\ {{\rm{t}} \ne q} \end{array}}^R {\left( {\begin{array}{*{20}{l}} {{r_t} + {m_t} - 1}\\ {{m_t}} \end{array}} \right)} } \frac{{\chi _t^{{r_t}}}}{{{{\left( {{\chi _x} - {\chi _q}} \right)}^{{r_t} + {m_t}}}}} $

最后，式(5)中计算的平均PEP将通过上边界技术计算平均误码率(BER, bit error rate)

$ {P_{{\rm{ber}}}} = \frac{1}{{{2^B}}}\sum\limits_X {\sum\limits_{\hat x} {\frac{\delta }{B}} } P\left( {\boldsymbol{X} \to \hat X} \right) $

(7)

其中：B=NlbML²，δ是X和$ {\boldsymbol{\hat X}} $之间的不同位数.

2.2 碰撞概率分析

允许用户在IMMA中共享可用的时隙将导致冲突，因为一个时隙可以由一个以上的用户使用，如前面的示例所示.每个用户的时隙的激活取决于输入的数据位.假设均匀分布的数据位，N个用户中有n个用户具有相同比特的概率可以表示为

$ {P_n} = \left( \begin{array}{l} N\\ n \end{array} \right){\left( {\frac{{2L - 1}}{{{L^2}}}} \right)^n}{\left( {1 - \frac{{2L - 1}}{{{L^2}}}} \right)^{N - n}} $

(8)

因此，如果将碰撞概率P_col定义为一个时隙被2个以上的用户占用的概率，它可以数学地表示为

$ {P_{{\rm{col}}}} = \sum\limits_{n = 2}^N {\left( \begin{array}{l} N\\ n \end{array} \right){{\left( {\frac{{2L - 1}}{{{L^2}}}} \right)}^n}{{\left( {1 - \frac{{2L - 1}}{{{L^2}}}} \right)}^{N - n}}} $

(9)

从式(9)可以看出，QIMMA的碰撞概率比IMMA的碰撞概率要大，因为每个用户激活了个时隙.即使是这样，最终的误码率性能QIMMA相比IMMA还是更好一些，后面通过仿真可以证明.

2.3 ML计算复杂度分析

考虑公式$ \hat X = \arg \;{\min _{X \in \psi }}\parallel \boldsymbol{Y} - {\rm{diag}}\left( {\boldsymbol{HX}} \right)\parallel _{\rm{F}}^2 $，则最大似然检测算法的计算复杂度可表示为^[6]

$ {c_{{\rm{ML}}}} = \left( {4LN + 2L} \right){\left( {{L^2}M} \right)^N} $

(10)

其中，计算diag(HX)需要4NL次实数乘法，而计算公式中的范数需要2L次实数乘法，所以，计算‖Y－diag(HX)‖_F²一共需要(4NL+2L)次实数乘法.考虑到ML检测算法穷尽搜索的特性，其需遍历(L²M)^N次，因此需要计算(L²M)^N次，其中，M表示调制阶数.

3 低复杂度检测方法

针对QIMMA系统的稀疏特殊性，提出2种低复杂度检测算法并且跟已有的最小均方误差(MMSE, minimum mean square error)^[8]检测算法和二元粒子群算法(BPSO, binary particle swarm optimization)^[9]进行比较.首先，提出基于时隙的接收端球形译码检测(RSD, receiver sphere decoding)算法，RSD检测算法将对在球体内部的每个格点按深度优先的思想进行搜索，在搜索过程中，当一个格点路径已经搜索完成但仍在球体内时，就把该格点与接收向量之间的最小欧氏距离作为新的球体半径来进行更新.当L=N时，为了降低QIMMA系统中最大似然检测算法的计算复杂度，提出基于时隙组合排序算法的接收端球形译码检测算法(BS-RSD, based sorting of receiver sphere decoding). BS-RSD检测算法的主要思想就是：在保证搜索格点存在的基础上，通过采用在搜索过程中改变搜索格点的次序，来让最有可能成为最优解的格点先被搜索到，以此来有效地加快搜索半径收敛，减少搜索次数，从而降低复杂度.

3.1 RSD检测算法

RSD的搜索方法的检测器可表示为

$ \boldsymbol{\hat X} = \arg \mathop {\min }\limits_{X \in \psi } \left\{ {\sum\limits_{i = 1}^{{{\left( {M{L^2}} \right)}^N}} {\sum\limits_{r = 1}^{\tilde L} {|\boldsymbol{Y}\left( {\boldsymbol{r}, :} \right) - \left( {\boldsymbol{H}\left( {\boldsymbol{r}, :} \right){\boldsymbol{X}_i}\left( {:, \boldsymbol{r}} \right)} \right){|^2}} } } \right\} $

(11)

其中：X_i(:, r)为ψ中第i个传输矩阵的第r列；$ \tilde L $为计算|Y(r, :)－(H(r, :)X_i(:, r))|²的层数，即搜索深度，其具体表达式可写为

$ \tilde L = \mathop {{\rm{argmax}}}\limits_{\begin{array}{*{20}{c}} {X \in \Omega }\\ {l \in \left\{ {1, 2, \cdots , L} \right\}} \end{array}} \left\{ {l|\sum\limits_{i = 1}^{{{\left( {M{L^2}} \right)}^N}} {\sum\limits_{l = 1}^L {|\boldsymbol{Y}\left( {l, :} \right) - \left( {\boldsymbol{H}\left( {l, :} \right){\boldsymbol{X}_i}\left( {:, l} \right)} \right){|^2}} } } \right\} ＜ {R^2} $

(12)

其中：Y(l, :)为接收矩阵的第l行；H(l, :)为第l时隙信道增益子矩阵，即信道矩阵的第l行；X_i(:, l)为ψ中第i个传输矩阵的第l列.

半径R可以选择为R=2αLσ²，其中α是一个常数，它的选取是为尽可能地保证目标格点在预先设定的球体半径之中.

对RSD接收机的复杂性进行分析. H(l, :)X_i(:, l)需要4N次实数乘法，求欧氏距离|·|²需要2L次计算复杂度，而且时隙为L, 用户数为N，调制阶数为M的QIMMA方案一共有(ML²)^N个可能传输的矩阵，所以，RSD检测算法的计算复杂度可表示为

$ {G_{{\rm{RSD}}}} = \left( {4N + 2L} \right){\left( {\sum\limits_{{l_\Re } = 1}^L {\sum\limits_{{l_\Im } = 1}^L {\sum\limits_{{x_\Re } = 1}^{\sqrt M } {\sum\limits_{{x_\Im } = 1}^{\sqrt M } {\tilde L} } } } } \right)^N} $

(13)

其中搜索次数满足$ 1 \le \tilde L \le L $.很容易证明C_QIMMA-RSD的复杂度为

$ \begin{array}{c} \left( {4N + 2L} \right) + 4{\left( {{L^2}M - 1} \right)^N} \le \\ {C_{{\rm{RSD}}}} \le \left( {4N + 2L} \right){\left( {{L^2}M} \right)^N} \end{array} $

(14)

具体来说，在最佳情况下，假设在对第1个格点进行搜索时，就检测出了最优解向量，则对其余剩下的各个格点的搜索只需要进行一层搜索即可，即当搜索第1个格点时，$ \tilde L = L $，而搜索其余格点时，$ \tilde L = 1 $，因此可得到RSD检测算法计算复杂度的最小值，表示为(4N+2L)+4(L²M－1)^N.在最坏情况下，也就是信噪比较小即噪声干扰较大的情况下，在对格点进行搜索时，每个格点都需要搜索L层，即需要搜索到最后一个格点才能检测出最优解向量，则此时可得到RSD检测算法计算复杂度的最大值，为(4N+2L)(L²M)^N.即使在最坏情况下，RSD检测算法的复杂度也比ML要低.

3.2 BS-RSD检测算法

当L=N时，信道矩阵和发送的X矩阵都为方阵，此时可用BS-RSD算法，首先提出了一种排序算法来对可能的时隙进行排序^[8].更具体地说，计算每个信道行的伪逆以预处理接收的矢量Y.其可用公式表示为

$ {p_k} = {\left( {{h_k}} \right)^† }\boldsymbol{Y} $

(15)

其中：$ {\left( {{h_k}} \right)^† } = \frac{{h_k^{\rm{H}}}}{{h_k^{\rm{H}}{h_k}}}, k \in \left\{ {1, 2, \cdots , L} \right\} $.

由式(15)可得各个发送时隙信道增益向量对接收向量Y预处理过后的矩阵P=[p₁, p₂, …, p_L]^T.由于QIMMA系统中每个用户需要激活2个时隙来发送空间符号的实部和虚部，所以为增强每种发送时隙组合的检测准确性，将引入一个加权因子w_i，其具体定义为

$ {w_i} = p_{i{1_{{l_\Re }}}}^2 + p_{i{1_{{l_\Im }}}}^2 + \cdots + p_{i{N_{{k_\Re }}}}^2 + p_{i{N_{{k_\Im }}}}^2 = \sum\limits_{n = 1}^N {p_{in{l_\Re }}^2 + p_{in{l_\Im }}^2} $

(16)

其中：i∈{1, 2, …, L′}，p_inlℜ表示第n个用户在第i个时隙传输符号实部，p_inlℑ²表示第n个用户在第i个时隙传输符号虚部，L′表示所有可能的发射时隙的组合数，且L′=L×L，l_ℜl_ℑ∈{1, 2, …, L}.

然后可根据上式得出每种发送天线组合经过加权因子w_i处理过的矩阵W=[w₁, w₂, …, w_L′]，接下来对矩阵W进行加权因子排序，可得到发送天线组合排序过后的矩阵K.

$ K = \left[ {{k_1}, {k_2}, \cdots , {k_{L'}}} \right] = \arg \;sort\left( \boldsymbol{W} \right) $

(17)

其中sort()表示对输入矩阵里面的元素以降序的方式进行重新排列的排序函数.

经过排序算法过后，再进行球形译码深度优先的搜索方法来检测，可表示为

$ \boldsymbol{\hat X} = \arg \mathop {\max }\limits_{X \in \Omega } \left\{ {\sum\limits_{i = 1}^{{{\left( {M{L^2}} \right)}^N}} {\sum\limits_{r = 1}^{\tilde L} {|\boldsymbol{Y}\left( {r, :} \right) - \left( {\boldsymbol{H}\left( {r, :} \right){\boldsymbol{X}_i}\left( {:, r} \right)} \right){|^2}} } } \right\} $

(18)

其中：Ω表示经过排序算法后可能的发送矩阵的集合，Ω是一个1×(ML²)^N的cell元胞数组，里面的每一个元素是一个N×L的矩阵，即发送矩阵X.$ \tilde L $表示计算|Y(r, :)－(H(r, :)X_i(:, r))|²的层数，即搜索深度.其具体表达式可写

$ \tilde L = \mathop {{\rm{argmax}}}\limits_{\begin{array}{*{20}{c}} {X \in \Omega }\\ {l \in \left\{ {1, 2, \cdots , L} \right\}} \end{array}} \left\{ {l|\sum\limits_{i = 1}^{{{\left( {M{L^2}} \right)}^N}} {\sum\limits_{l = 1}^L {|\boldsymbol{Y}\left( {l, :} \right) - \left( {\boldsymbol{H}\left( {l, :} \right){\boldsymbol{X}_i}\left( {:, l} \right)} \right){|^2}} } } \right\} ＜ {R^2} $

(19)

其中：Y(l, :)表示接收矩阵的第l行，H(l, :)表示第l时隙信道增益子矩阵，即信道矩阵的第l行. X_i(:, l)表示Ω里面第i个传输矩阵的第l列.

BS-RSD检测算法关键搜索过程如下.

输入:Y, H, 传输矩阵集合Ω，初始半径R；

输出：估计发送符号实部时隙$ {{\hat l}_\Re } $和虚部时隙$ {{\hat l}_\Im } $，估计发送星座符号实部$ {{\hat s}_\Re } $和虚部$ {{\hat s}_\Im } $

1    $ P = {\left[ {{p_1},{p_2}, \cdots ,{p_L}} \right]^{\rm{T}}},{p_k} = {\left( {{h_k}} \right)^† }Y,{\left( {{h_k}} \right)^† } = \frac{{h_k^H}}{{h_k^H{h_k}}} $

2    $ \boldsymbol{W} = \left[ {{w_1}, {w_2}, \cdots , {w_{L'}}} \right], {w_i} = \sum\limits_{n = 1}^N {p_{i{n_{{l_\Re }}}}^2 + p_{i{n_{{l_\Im }}}}^2} , {l_\Re }, {l_\Im } \in \left\{ {1, 2, \cdots , L} \right\} $

3    i=1

4    where i≤(ML²)^N

5        for r≤L

6            δ(i)+=|Y(r, :)－(H(r, :)X_i(:, r))|²

7              if δ(i)≥R²

8                  r=r+1;

9              End if

10                R²=δ(i)

11      $ \hat X = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \left( i \right) $

12      $ \left[ {{{\hat l}_\Re }, {{\hat l}_\Im }, {{\hat s}_\Re }, {{\hat s}_\Im }} \right] = \mathop {\arg \;\min }\limits_{{{\hat l}_\Re }, {{\hat l}_\Im }, {{\hat s}_\Re }, {{\hat s}_\Im } \in \Omega } \left( {\delta \left( i \right)} \right) $

BS-RSD检测算法的计算复杂度可分为对发送时隙组合排序的计算复杂度和球形译码检测的计算复杂度两大部分.发送时隙组合排序部分的计算复杂度：根据式(15)，需要(4N+2N+4N)L次实数乘法，而根据式(16), 在计算$ {w_i} = \sum\limits_{n = 1}^N {p_{in{l_\Re }}^2 + } p_{in{l_\Im }}^2 $时需要4NL次实数乘法.球译码检测部分计算复杂度与RSD检测算法完全相同，这里就不再叙述.最终BS-RSD检测算法的复杂度为这2部分复杂度相加的和，即

$ \begin{array}{*{20}{l}} {{G_{{\rm{BS - RED}}}} = 14NL + \left( {4N + 2L} \right){{\left( {\sum\limits_{{l_\Re }}^L {\sum\limits_{{l_\Im }}^L {\sum\limits_{{x_\Re }}^{\sqrt M } {\sum\limits_{{x_\Im }}^{\sqrt M } {\tilde L} } } } } \right)}^N}} \end{array} $

(20)

3.3 MMSE检测算法

MMSE检测以最小均方误差为目标，即最小化时隙发送信号与检测估计信号之间的均方误差，其最优化问题可以表示为

$ \mathop {\min }\limits_G E\left[ {\parallel \boldsymbol{s} - G\boldsymbol{y}\parallel _{\rm{F}}^2} \right] $

(21)

式(21)的最优解向量可以通过运算得到

$ {G_{{\rm{MMSE}}}} = {\left( {{\boldsymbol{H}^{\rm{H}}}\boldsymbol{H} + {\sigma ^2}{\boldsymbol{I}_L}} \right)^{ - 1}}{\boldsymbol{H}^{\rm{H}}} $

(22)

则该检测算法的计算复杂度为

$ \left( {2{L^3} + 3{L^2} - 5L} \right)/6 + 2N{L^2} + NL + 8L \times 4M $

4 仿真结果

这部分给出了所提出的QIMMA方案在瑞利衰落信道下的蒙特卡洛仿真结果和分析.

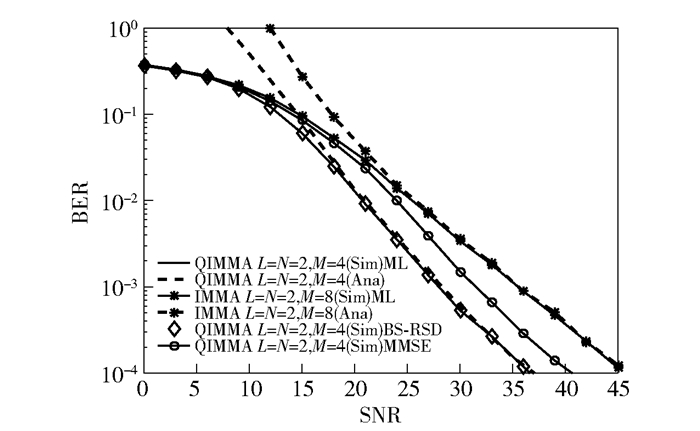
图 2显示了IMMA和QIMMA方案在每个用户的频谱效率为4 bit·s^-1·Hz^-1时的误码率与信噪比之间的关系.可见，QIMMA方案误码率性能远优于IMMA系统的性能，即使在冲突概率增大的情况下.在误码率为10^－3时，QIMMA比IMMA性能好大约8 dB.另外，图中比较了ML和BS-RSD，MMSE的性能，从图中可以看出，BS-RSD可以达到最优性能，而MMSE比最优性能差3 dB左右.

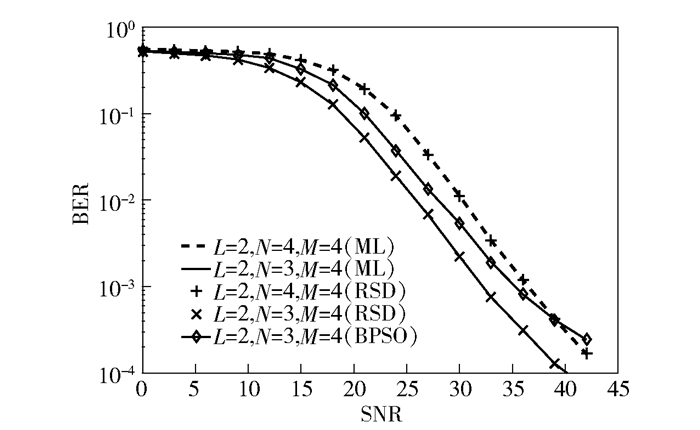
图 3所示为在[L, N]=[2,2]情况下，ML和RSD以及BPSO检测算法的误码率性能.对BPSO检测算法，复杂度可以使用总搜索次数来衡量，即T×K，其中T表示粒子数，K表示最大迭代次数.在计算时，设置T×K=3 000，使BPSO检测算法复杂度相比ML检测算法降低约25%.从图中可以看出，QIMMA系统中，在不同的调制阶数配置下，RSD检测算法基本能够达到ML检测算法的最优误码率性能, 而BPSO算法性能明显差一些.另外，从图中还可以看出，随着用户数N的增多，系统误码性能变差.

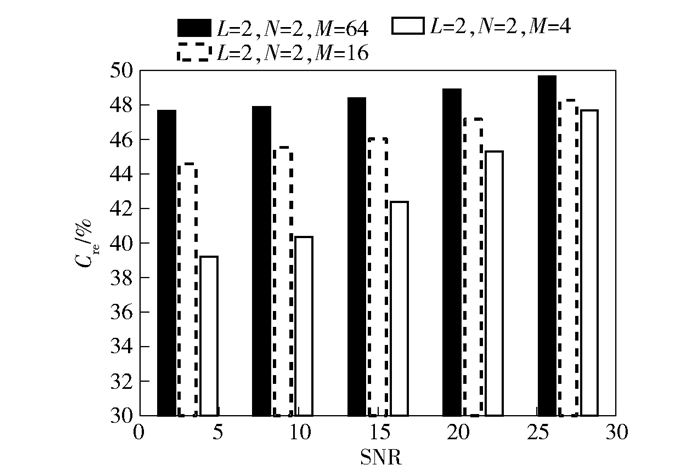
图 4所示为在[L, N]=[2,2]情况下，当调制阶数M=4、16、64时，BS-RSD检测算法相对于ML检测算法降低的复杂度百分比.定义相对计算复杂度减少量为C_re(%)=100×(C_ML-C_BS-RSD)/C_ML.从图 4中可以看出，随着M的增大，BS-RSD降低的复杂度也随之变大.在64QAM时计算复杂度减少量可以达到接近50%.

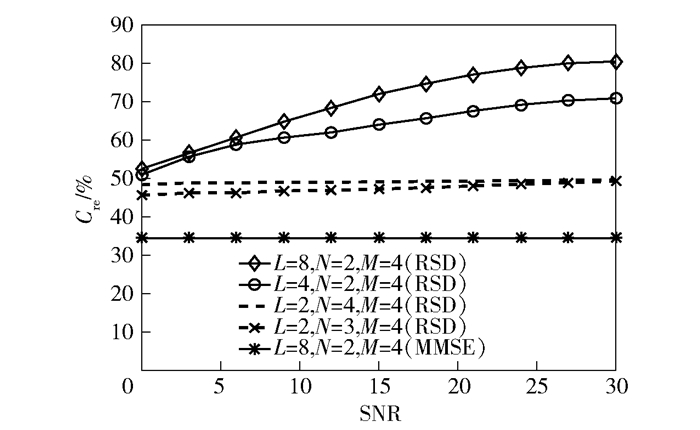
图 5所示为QIMMA系统下，M=4时，随L、N的变化RSD和MMSE算法复杂度的变化.定义纵坐标为C_re(%)=100×(C_ML-C_RSD/MMSE)/C_ML.从图 5可以看出，当N=2时，L越大，RSD复杂度降低的越多，且信噪比越大，复杂度降低的越多，最多能够降低80%以上.这是由于当系统信噪比较高时，RSD算法能够更加准确地检测出发送天线组合，从而加速搜索半径收敛，使得搜索次数显著减少.另外从图中还可以看出，当L=2时，随着N的增大，复杂度降低得越多，逐渐趋近于50%.而MMSE算法在L=8时复杂度只降低30%多.

5 结束语

基于最近提出QIMMA系统，进行了理论性能分析和低复杂度检测.提出了接收端球形译码准则的2种低复杂度检测算法.蒙特卡洛仿真结果表明，提出的RSD和BS-RSD检测算法与经典的ML检测算法相比，在性能达到最优的前提下能降低至少1/3的复杂度，而且随着时隙的增加，甚至可以降低80%以上的复杂度.因此，QIMMA具有极大的潜力，可满足第5代移动通信系统无线用户数量的增长和对高数据率的需求，有效缓解频谱稀缺和能源资源有限的问题.