2. 湖南省铀尾矿库退役治理技术工程技术研究中心, 衡阳 421001;
3. 铀矿冶放射性控制技术湖南省工程研究中心, 衡阳 421001
为了提高启发式定位算法的搜索效率和定位精度,提出了基于罚函数和水波优化的无线传感器网络(WSN)定位算法.首先利用bounding-box方法构造罚函数,提高算法搜索的效率和定位精度;然后利用动态学习策略对传统水波优化算法的传播阶段进行改进,促使个体对周围优秀个体的学习,并通过动态波高提高个体在后期局部搜索的概率,进一步提高搜索效率和求解精度.仿真结果表明,罚函数策略与改进水波优化算法能提高搜索效率和定位精度,所提出的算法在WSN节点定位上有较好的可行性和有效性.
2. Hunan Province Engineering Technology Research Center of Uranium Tailings Treatment Technology, Hengyang 421001, China;
3. Hunan Province Engineering Research Center of Radioactive Control Technology in Uranium Mining and Metallurgy, Hengyang 421001, China
In order to improve the search efficiency and localization accuracy of the heuristic localization algorithm, a localization algorithm base on penalty function and water wave optimization for wireless sensor network (WSN) is proposed. Firstly, the proposed algorithm uses the bounding-box method to construct the penalty function, which improves the water wave optimization algorithm's searching efficiency. Then the dynamic learning strategy is used to improve the propagation stage of the traditional water wave optimization algorithm, which encourages the individual to learn from the surrounding excellent individuals. And the dynamic wave height is introduced to enhance the individual's local search probability in late stage. Simulations show that the penalty function strategy and the improved water wave optimization algorithm can improve the search efficiency and positioning accuracy. The proposed algorithm has good feasibility and effectiveness in WSN node location.
无线传感器网络(WSN, wireless sensor network)是由具有通信能力的传感器节点组成的分布式传感网络,目前在环境监测、农业、智能家居与医疗健康等领域得到广泛应用[1].在WSN系统中定位被认为是一项必不可少的关键技术,位置信息有助于准确感知监测对象状态,并帮助决策者做出正确合理的决策[2].
目前有许多学者提出不同的定位算法,其中根据其是否需要测距分为基于测距和非测距两大类算法.非测距类算法的定位精度较低,且其对网络连通性要求高;而测距类算法对部署环境要求较低,因此其适应性更好.在众多的测距方法中,如基于到达时间测距[3]、基于到达时间差测距[4]等都需要额外的硬件,提高了节点成本,不利于大规模的WSN部署,而基于接收信号强度(RSSI, received signal strength indication, )的测距方法不需要额外硬件就能得到较好的精度,这也使得其成为定位研究的一个热点.基于测距的定位算法目前已经有许多研究成果,如王中元等[5]针对现实中三维空间定位,提出了空间球交会的三维加权质心定位算法;汪晗等[6]针对分布式迭代定位中误差的传播和累积问题,提出了利用几何精度因子来控制权值,从而有效地降低了误差的传递;Wei等[7]将压缩感知应用到节点定位中,减少信号测量的冗余,提高定位的实时性.
近些年,由于启发式算法极强的适应性和高效性,已经应用到了许多领域中,如电力系统调度[8]、应急设施的选址[9]、流水作业的调度等[10].许多学者也将其应用到WSN未知节点求解优化问题中,如Chen等[11]提出了利用改进无迹卡尔曼滤波与粒子群优化(PSO, particle swarm optimization)算法相结合,减小定位误差;Goyal等[12]改进蝙蝠算法对定位问题进行求解,提高定位精度;Cheng等[13]提出了基于布谷鸟搜索的节点定位算法;Bao等[14]提出了基于移动信标节点的定位算法,并利用PSO算法求解最优估计位置.上述启发式算法在求解最优估计位置时,存在搜索效率较低、定位误差较大等缺陷.因此,笔者提出基于罚函数与水波优化(WWO, water wave optimization)的WSN定位算法.首先利用初步的测距信息构造一个罚函数,提高算法前期搜索效率,然后采用改进WWO算法进一步提高搜索效率与求解精度.仿真实验结果表明,所提算法的定位效果更好,罚函数策略与改进WWO算法能进一步提高节点的定位精度.
1 基于罚函数的节点定位模型 1.1 RSSI测距RSSI测距模型利用信号在空间中的衰减特性,构建信号强度与距离之间的数值关系.节点利用信号接收器接收邻居节点的数据包,并得到该数据信号的信号强度值,通过信号强度与距离之间的数值关系得到节点间的距离.常用的对数正态分布模型为
| $ P\left( d \right) = P\left( {{d_0}} \right) - 10\alpha \lg \left( {\frac{d}{{{d_0}}}} \right) + {X_\sigma } $ | (1) |
其中:P(d)代表距离为d时节点接收到的信号强度;d0为参考距离;P(d0)为在参考距离节点接收到的信号强度;α为与环境相关的路径衰减指数;Xσ代表以σ为标准差,均值为0的高斯噪声.
1.2 节点定位模型设节点Si的位置未知,其通信范围内有m个信标节点,坐标为(xj,yj),j=1, 2, ..., m,利用式(1)得到未知节点Si与信标节点j的估计距离
| $ \begin{array}{c} \arg \;\mathop {{\rm{min}}}\limits_{\left( {{{\hat x}_i}, {{\hat y}_i}} \right)} \frac{1}{m}{\left( {\sqrt {{{\left( {{{\hat x}_i}, {x_j}} \right)}^2} + {{\left( {{{\hat y}_i}, {y_j}} \right)}^2}} - {d_{ij}}} \right)^2}\\ j = 1, 2, \cdots , m \end{array} $ | (2) |
许多学者通过群体优化算法对上述问题进行求解,如PSO算法、布谷鸟优化、人工蜂群算法等.但是,这些群体优化算法在前期需要对整个部署区域进行搜索,计算量较大,且收敛的速度较慢,精度低.因此,为了提高前期群体搜索的有效性,加快收敛速度,笔者提出利用bounding-box方法(见图 1)获取待定位节点位置的初步信息,并利用该信息构建一个有效的罚函数,提高群体优化算法群体搜索的有效性.

|
图 1 Bounding-box方法示意图 |
如图 1所示,传统的bounding-box方法通过估计距离
| $ \left. {\begin{array}{*{20}{c}} {{{\hat x}_i} \in \left[ {{x_j} - {d_{ij}}, {x_i} + {d_{ij}}} \right]}\\ {{{\hat y}_i} \in \left[ {{y_j} - {d_{ij}}, {y_i} + {d_{ij}}} \right]} \end{array}, j = 1, 2, \cdots , m} \right\} $ | (3) |
由式(3)得到每个方形区域后,可以计算得到重叠部分边界值.未知节点有较大概率在该区域内部或周边,为了驱使搜索个体搜索bounding-box区域附近,对处于区域外的个体给予惩罚,并且距离边界越远惩罚值越大,对处于区域内的个体惩罚值设置为零.在搜索过程中每个个体的位置代表问题的解,搜索个体i的惩罚值P(i)为
| $ P\left( i \right) = {k_{\rm{p}}}\left[ {{k_x}{\rm{Dist}}\left\langle {{{\hat x}_i}, {L_x}} \right\rangle + {k_y}{\rm{Dist}}\left\langle {{{\hat y}_i}, {L_y}} \right\rangle } \right] $ | (4) |
其中:
| $ \begin{array}{c} {\rm{fit}}\left( i \right) = \\ \frac{1}{m}\left( {\sum\limits_{j = 1}^m {{{\left( {\sqrt {{{\left( {{{\hat x}_i} - {x_j}} \right)}^2} + {{\left( {{{\hat y}_i} - {y_j}} \right)}^2}} - {d_{ij}}} \right)}^2} + P\left( i \right)} } \right), \\ j = 1, 2, \cdots , m \end{array} $ | (5) |
通过求解式(5)的最小值对应的个体位置,即求得未知节点的估计位置.
2 基于WWO的节点定位算法 2.1 WWO算法受浅水波理论的启发,郑宇军教授在2015年提出新型启发式算法——WWO算法[15].该算法具有简单、容易实现和算法参数少等优点.在WWO算法中,问题空间类比为海床,种群中的每个个体类比于一个“水波”对象,每个水波有2种属性:初始波高h和波长λ.WWO算法的核心是为每个解分配与其适应度成反比的波长,并使每个解传播(搜索)范围与其波长成正比:距离海平面越近的点,对应的解越优,相应的水波越高,那么水波的波高越大,波长越小.WWO算法主要通过模拟水波的传播、折射和碎浪3个操作,在问题空间中进行高效搜索.不失一般性,下面以求解最大值为例介绍WWO算法.
1) 传播阶段.每次迭代所有水波个体都需要进入传播阶段,传播过程在每一维的表达式为
| $ s'\left( d \right) = s\left( d \right) + {N_r}\lambda L\left( d \right) $ | (6) |
其中:Nr为区间[-1, 1]的随机数,λ为水波波长,L(d)为解空间在维度d的长度,s(d)为s个体在d维度的位置,s′(d)为传播过程后的水波在d维度的位置.若新个体超出边界,则赋予新个体在该维度搜索空间中的随机位置.传播过程完成后,计算传播产生的新个体适应度值,若fit(s′)>fit(s),则s′替代s,更新波高为初始波高hmax,否则波高h减1.若新个体优于原个体且优于群体最优个体,则进入碎浪阶段.每轮迭代完成后,所有水波按照式(7)更新波长.
| $ \lambda = \lambda {\theta ^{ - \left[ {{\rm{fit}}\left( s \right) - {F_{\min }} + \varepsilon } \right]/\left( {{\rm{fi}}{{\rm{t}}_{\max }} - {\rm{fi}}{{\rm{t}}_{\min }} + \varepsilon } \right)}} $ | (7) |
其中:fitmax与fitmin分别为群体最大适应度值和最小适应度值;θ为波长衰减因子;ε为一个微小的正常数,防止分母为0.
2) 折射阶段.判断水波个体波高h是否为0.若水波波高h减为0,则通过式(8)折射操作产生下一代个体;若波高h不为0,则该个体进入下一轮迭代.
| $ s'\left( d \right) = N\left( {\frac{{{s^*}\left( d \right) + s\left( d \right)}}{2}, \frac{{|{s^*}\left( d \right) - s\left( d \right)|}}{2}} \right) $ | (8) |
式中:s*为种群中最佳个体,N(μ, σ)为均值为μ、标准差为σ的高斯随机数.完成折射过程后将波高更新为hmax,根据式(9)更新该个体的波长λ′;若适应度值为负,则按照式(9)更新波长后取倒数.
| $ \lambda ' = \lambda \frac{{{\rm{fit}}\left( s \right)}}{{{\rm{fit}}\left( {s'} \right)}} $ | (9) |
3) 碎浪阶段.当群体发现有新个体适应度值优于目前群体最佳个体s*时,则进行碎浪.碎浪主要过程为随机选取k个维度在s*个体周边产生k个搜索个体搜索s*附近区域.新水波个体在选取维度上按照式(10)更新得到新个体.
| $ s'\left( d \right) = s\left( d \right) + \beta N\left( {0, 1} \right)L\left( d \right) $ | (10) |
其中:β为碎浪因子,L(d)为d维度的搜索区间长度.若产生的水波个体适应度值没有优于s*个体,则s*保留,否则产生的最优个体替代s*.
2.2 改进WWO定位算法WWO算法作为一种新型的启发式算法,它通过模拟水波的传播过程来求解优化问题,求解过程中主要由传播、折射和碎浪3个步骤来更新个体寻求最优.在传播阶段,水波种群在求解区域中按照式(6)得到下一代位置,该过程主要是通过随机的方式搜索更优位置.水波在传播过程中未搜索到更优个体且波高降为0时进入折射阶段,在折射过程中,水波按照式(8)更新得到新位置,该过程实际是在向最优个体学习,在收敛后期相当于在个体与最优个体周围进行搜索.每当个体找到新的全局最优时则进入碎浪阶段,在碎浪步骤中按照式(10)在全局最优个体周围生成新个体,将其与原最优值进行比较,按照优胜劣汰的方式保留最优个体作为全局最优个体,该过程实际上是在最优个体附近进行局部搜索寻求更优.然而,算法在传播阶段使用搜索效率较低的随机方式更新个体,在后期搜索几乎停滞时对周围区域探索较少,不利于跳出局部最优,因此提出基于动态学习的传播阶段与动态波高策略.
2.2.1 基于动态学习的传播阶段由式(6)可知,传播阶段的步长是在指定范围内均匀分布的随机数,并且有可能超出搜索边界,这种搜索方式虽然简单,但其搜索的有效性较低,算法收敛速度慢.针对上述问题,提出在传播阶段个体更新过程中引入动态学习策略,提高水波个体传播阶段搜索的有效性.动态学习的传播阶段主要由2部分组成,一是向距离自己最近且适应度值优于自身的个体学习;二是随机部分.原水波个体s在该过程每个维度上的更新值s′(d)表示为
| $ \begin{array}{l} s'\left( d \right) = s\left( d \right) + {N_r}\lambda L\left( d \right) + {w_{\rm{L}}} \times \\ \;\left( {\frac{{{\rm{fi}}{{\rm{t}}_s} - {\rm{fi}}{{\rm{t}}_{\max }}}}{{{\rm{fi}}{{\rm{t}}_{\min }} - {\rm{fi}}{{\rm{t}}_{\max }}}}} \right)\left[ {{s_{\rm{L}}}\left( d \right) - s\left( d \right)} \right] \end{array} $ | (11) |
其中:s′为更新得到个体;wL为学习因子,取0~1之间的随机数;sL为距离个体最近且适应度值优于自身的个体;fits为个体s的适应度值;fitmax与fitmin分别为群体中适应度最优与最劣值.从式(11)中可以看到,当原水波个体s的适应度值较差时,则学习部分的权重值较大;当原水波个体s的适应度值较优时,则学习部分的权重值较小;当原水波个体s的适应度值为群体最优时,则学习部分权重为0,这时主要通过随机部分搜索传播后位置.通过上述机制,水波个体在适应度较差时通过向周围优秀个体学习提高搜索效率,同时利用随机部分增加个体多样性,提高算法收敛速度.
2.2.2 动态波高策略当初始波高hmax设置较大时,水波进入折射阶段概率较低;当初始波高hmax设置较小时,水波有更大概率进入折射阶段.算法在求解前期通过传播阶段对求解空间进行探索,在收敛后期,由于求解函数的局部最优集中在实际最优解附近,算法容易陷入局部最优,因此应更多进入折射阶段在个体与全局最优周围探索,寻求更优位置.针对上述分析,提出了动态波高策略,该策略利用迭代次数控制初始波高hmax,使得hmax随着迭代次数的增加逐渐减小.初始波高随着迭代次数的变化为
| $ {h'_{\max }} = {\mathop{\rm int}} \left[ {{h_{\max }} \times \exp \left( { - \frac{t}{{{t_{\max }}}}} \right)} \right] $ | (12) |
其中:h′max为每轮迭代后初始波高的更新值,t为当前迭代次数,tmax为最大迭代次数,int表示取整.改进WWO定位(IWWOP, improved WWO positioning)算法的伪代码如算法1所示.
算法1 IWWOP算法
输入:未知节点与其通信半径内信标节点的估计距离;
输出:未知节点的估计位置.
1 在空间中初始化水波种群Sw,初始化迭代次数t = 0;
2 计算每个水波个体的适应度值fit,保存群体的最优值s*;
3 While t⇐tmax
4 For水波s in Sw Do
5 进入传播阶段,按照式(11)产生s′;
6 If fit(s′)>fit(s)
7 个体s′取代s,更新其波高为初始波高hmax;
8 If fit(s′) > fit(s*)
9 更新s*进入碎浪阶段,按照式(10)产生搜索周围区域,若有更优个体则替换s*为更优个体,更新其波高为初始波高hmax;
10 End
11 Else
12 水波s的波高h减1;
13 End
14 If s的波高h=0
15 进入折射阶段,按照式(8)、式(9)更新个体位置和波长,更新其波高为初始波高hmax;
16 End
17 按照式(7)更新所有个体波长;
18 按照式(12)更新初始波高;
19 t=t+1;
20 End
21 End
22 输出最佳个体所在位置.
3 仿真实验与分析 3.1 基本实验参数设置为了验证提出算法的有效性,在Matlab平台中进行仿真实验,实验主要对比了PSO、WWO、WWOP与IWWOP 4种算法.其中,PSO代表使用PSO求解不含罚函数的节点定位算法,WWO代表求解不含罚函数的传统WWO定位算法,WWOP代表基于罚函数的传统WWO定位算法,IWWOP代表所提出的基于罚函数与WWO的WSN定位算法.仿真实验参数如表 1所示.
|
|
表 1 实验参数设置 |
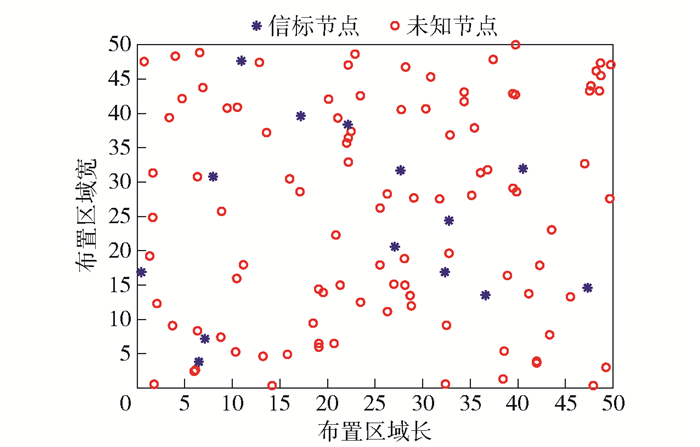
设置信标节点个数为15,未知节点个数为100,节点布置如图 2所示.
|
图 2 节点布置 |
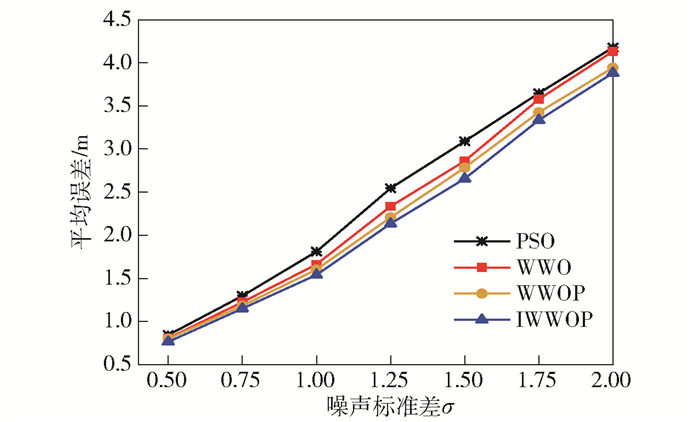
设置通信半径为30 m,RSSI噪声标准差为0.5~2,迭代次数为50.图 3对比了100个未知节点,4种算法在不同噪声条件下的平均误差.
|
图 3 噪声与误差 |
由图 3可以看出,随着噪声的增加,节点定位的平均误差也逐渐增加.当噪声标准差为0.5时,PSO算法与WWO算法的平均误差分别为0.84 m与0.81 m,WWOP算法与IWWOP算法的平均误差分别为0.80 m与0.76 m;当噪声标准差为2时,PSO算法与WWO算法的平均误差分别为4.18 m与4.13 m,WWOP算法与IWWOP算法的平均误差分别为3.94 m与3.88 m.随着噪声增加过程中,误差最大的为PSO算法,其次为WWO算法和WWOP算法,最小的为IWWOP算法,这主要是因为提出的罚函数策略与改进WWO算法能改善定位精度.
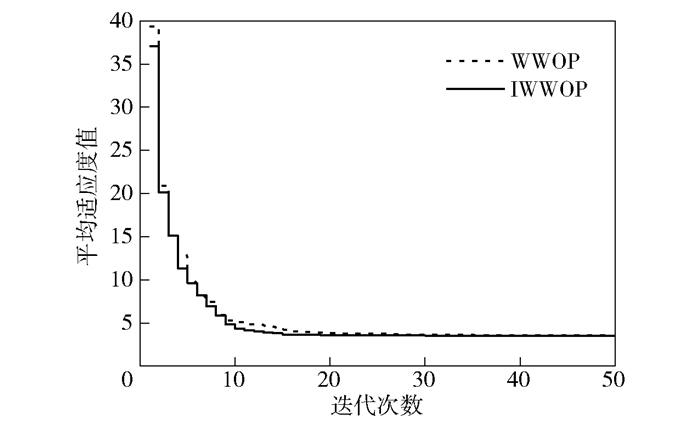
以式(5)为目标函数,设置信号噪声标准差为1,对100个未知节点求解过程中,WWOP与IWWOP两种算法的平均适应度值与迭代次数的关系如图 4所示.
|
图 4 算法优化对比 |
由图 4可以看出,2种算法的适应度值随着迭代次数的增加逐渐降低.其中,IWWOP算法下降得最快,在13次左右收敛,而WWOP算法在20次左右逐渐收敛.当迭代次数为15时,IWWOP算法的平均适应度值为3.67,WWOP算法的平均适应度值为4.22;当迭代次数为30时,IWWOP算法的平均适应度值为3.55,WWOP算法的平均适应度值为3.65;当迭代次数增加到50时,IWWOP算法的平均适应度值为3.51,WWOP算法的平均适应度值为3.55.由上述分析可以得到,加入了学习和动态波高策略的IWWOP算法在求解问题上的收敛速度与求解精度都优于WWOP算法.
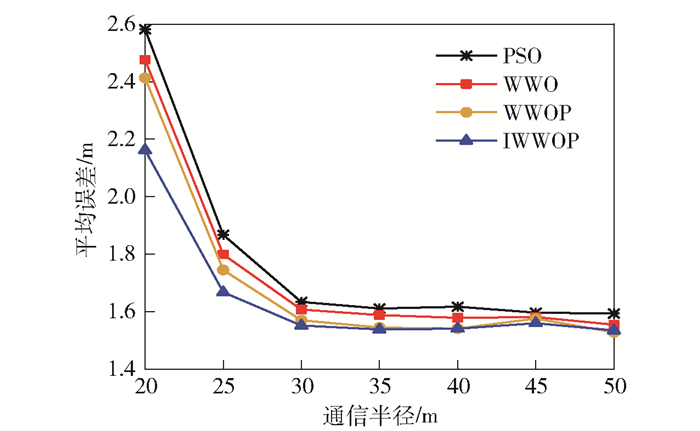
设置信号噪声标准差为1,迭代次数为50,通信半径为15~50 m,通信半径对误差的影响如图 5所示.
|
图 5 通信半径与误差 |
由图 5可以看到,未知节点的平均定位误差随着通信半径的增加逐渐降低,当通信半径下降到30 m时误差降低的速度减缓,这主要是由于通信距离的增加,未知节点有更多的信标节点作为参考,提高了节点的定位精度.整个过程中定位精度最高的为IWWOP算法,其次分别为WWOP算法与WWO算法,最低的为PSO算法.
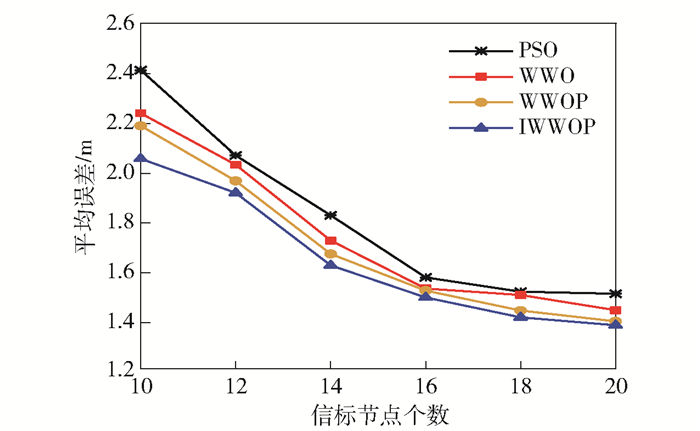
设置噪声标准差为1,迭代次数为50,通信半径为30 m,信标节点个数为10~20,信标节点对定位误差的影响如图 6所示.
|
图 6 信标节点个数与误差 |
由图 6可以看到,节点定位平均误差随着信标节点个数的增加而减少,这说明信标节点的数量越多,有利于降低节点的定位误差.这主要是因为信标节点数量越多,未知节点定位过程中获得关于位置的信息越多,从而提高了定位精度.整个过程中定位误差最小的为IWWOP算法,其次分别为WWOP算法和WWO算法,最大的为PSO算法.因此,提出罚函数策略和改进WWO算法在相同信标节点个数条件下能提高节点的定位精度.
4 结束语目前有许多学者将启发式算法应用到WSN节点定位求解中,但启发式算法在求解定位问题中存在搜索效率低、定位误差较大的问题,对此笔者利用bounding-box方法构造罚函数提高启发式算法的搜索效率,同时引入一种新型的WWO算法并对其改进,提高收敛速度与求解精度,进而提高节点的定位精度.仿真实验结果表明,改进策略能提高算法的定位精度,所提出的定位算法在定位上有较高的有效性.
| [1] |
Mesmoudi A, Feham M, Labraoui N. Wireless sensor networks localization algorithms:a comprehensive survey[J]. International Journal of Computer Networks & Communications, 2013, 5(6): 748-755. |
| [2] |
钱志鸿, 孙大洋, Leung Victor, 等. 无线网络定位综述[J]. 计算机学报, 2016, 39(6): 1237-1256. Qian Zhihong, Sun Dayang, Leung Victor, et al. A survey on localization model in wireless networks[J]. Chinese Journal of Computers, 2016, 39(6): 1237-1256. |
| [3] |
张玺栋, 张平, 康桂霞, 等. 智能天线辅助的WSN节点自定位算法[J]. 北京邮电大学学报, 2014, 37(2): 28-31. Zhang Xidong, Zhang Ping, Kang Guixia, et al. Smart antenna assisted WSN node self locating algorithm[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(2): 28-31. |
| [4] |
Singh P, Agrawal S. TDOA based node localization in WSN using neural networks[C]//International Conference on Communication Systems & Network Technologies.[S.l.]: IEEE, 2013: 400-404. https://www.researchgate.net/publication/261265072_TDOA_based_node_localization_in_WSN_using_Neural_networks
|
| [5] |
王中元, 程少博, 刘春燕, 等. 空间球交会的三维加权质心室内定位算法[J]. 中国矿业大学学报, 2016, 45(5): 944-950. Wang Zhongyuan, Cheng Shaobo, Liu Chunyan, et al. Three-dimensional weighted centroid indoor positioning algorithm based on sphere intersection[J]. Journal of China University of Mining & Technology, 2016, 45(5): 944-950. |
| [6] |
汪晗, 成昂轩, 王坤, 等. 无线传感器网络分布式迭代定位误差控制算法[J]. 电子与信息学报, 2018, 40(1): 72-78. Wang Han, Cheng Angxuan, Wang Kun, et al. Error control algorithm of distributed localization in wireless sensor networks[J]. Journal of Electronics & Information Technology, 2018, 40(1): 72-78. |
| [7] |
Wei Y, Li W, Chen T. Node localization algorithm for wireless sensor networks using compressive sensing theory[J]. Personal and Ubiquitous Computing, 2016, 20(5): 809-819. DOI:10.1007/s00779-016-0951-7 |
| [8] |
梁静, 葛士磊, 瞿博阳, 等. 求解电力系统经济调度问题的改进粒子群优化算法[J]. 控制与决策, 2020, 35(8): 1813-1822. Liang Jing, Ge Shilei, Qu Boyang, et al. Improved particle swarm optimization algorithm for solving power system economic dispatch problem[J]. Control and Decision, 2020, 35(8): 1813-1822. |
| [9] |
于冬梅, 高雷阜, 赵世杰. 可靠性应急设施选址多级覆盖鲁棒优化模型[J]. 中国矿业大学学报, 2019, 48(4): 919-927. Yu Dongmei, Gao Leifu, Zhao Shijie. A robust hierarchical covering optimization model for reliability emergency facility location[J]. Journal of China University of Mining & Technology, 2019, 48(4): 919-927. |
| [10] |
Shao Zhengshi, Pi Dechang, Shao Weishi. A novel discrete water wave optimization algorithm for blocking flow-shop scheduling problem with sequence-dependent setup times[J]. Swarm and Evolutionary Computation, 2018, 40: 53-75. DOI:10.1016/j.swevo.2017.12.005 |
| [11] |
Chen Xiao, Zou Shengnan. Improved wi-fi indoor positioning based on particle swarm optimization[J]. IEEE Sensors Journal, 2017, 17(21): 7143-7148. DOI:10.1109/JSEN.2017.2749762 |
| [12] |
Goyal S, Patterh M S. Modified bat algorithm for localization of wireless sensor network[J]. Wireless Personal Communications, 2015, 86(2): 657-670. |
| [13] |
Cheng Jing, Xia Linyuan. An effective cuckoo search algorithm for node localization in wireless sensor network[J]. Sensors, 2016, 16(9): 1390-1406. DOI:10.3390/s16091390 |
| [14] |
Bao Han, Zhang Baoxian, Li Cheng, et al. Mobile anchor assisted particle swarm optimization (PSO) based localization algorithms for wireless sensor networks[J]. Wireless Communications and Mobile Computing, 2012, 12(15): 1313-1325. DOI:10.1002/wcm.1056 |
| [15] |
Zheng Yujun. Water wave optimization:a new nature-inspired metaheuristic[J]. Computers & Operations Research, 2015, 55: 1-11. |



