2. 广西信息科学实验中心, 桂林 541004;
3. 桂林电子科技大学 计算机与信息安全学院, 桂林 541004
Massive-MIMO多用户系统中,现有能效(EE)和频效(SE)性能折中方法在单个目标优化时无法适应变化场景,进而无法对优化目标进行有效追踪.对此,提出了一种能够适应变化场景需求的能效和频效性能折中方法.通过构建折中优化函数,将非凸的多目标优化问题转化为单目标凸优化问题,并利用拉格朗日乘子法进行求解.理论分析和仿真结果表明,提出的性能折中方法能够在系统电路功耗的限制下,通过设定折中因子改变系统能效值或频效值,并同时获取能效和频效的最佳性能折中.
2. Guangxin Information Science Research Centre, Guilin 541004, China;
3. School of Computer and Information Security, Guilin University of Electronic Technology, Guilin 541004, China
In massive-multiple input multiple output (massive-MIMO) multi-user system, the existing energy efficiency (EE) and spectral efficiency (SE) trade-off performance methods cannot adapt to the changing scenarios for single objective optimization, and thus cannot effectively track the optimization objectives. To solve this problem, a trade-off method of energy efficiency and spectral efficiency is proposed, which can adapt to the changing scenarios. By constructing a trade-off optimization function between them, the non-convex multi-objective optimization problem is transformed into a single-objective convex optimization problem, and solved by Lagrange multiplier method. The theoretical analysis and simulation results show that the proposed trade-off method can change the system energy efficiency or spectral efficiency by setting a trade-off factor under the power consumption limitation of the system circuit, and simultaneously obtain the optimal performance trade-off of energy efficiency and spectral efficiency.
随着智能终端的兴起,高速移动业务的需求迅速增长,现有频谱资源匮乏及移动设备能耗过高的问题日益凸显[1-2].在频谱资源受限情况下,提高系统频效(SE,spectral efficiency)是解决频谱资源匮乏的有效手段.与此同时,降低在移动通信系统的高能耗并提高系统能效(EE,energy efficiency)是满足绿色通信和移动通信规模发展的需求[3-4].然而,在Massive-MIMO(MIMO,multiple input multiple output)系统中,能效和频效是一对相互制约的矛盾指标,优化其中一个指标,必然导致另一个指标的恶化[5].如何适应变化场景需求,在满足其中一个指标(频效或能效)要求的前提下,尽可能地使另一个指标(能效或频效)获得最大值,以获取能效和频效的最佳性能折中,引起了广泛的研究和关注.
Onireti和Héliot等[6-7]研究了能效与频效之间的关系,基于威纳模型提出了二者折中的近似关系闭式. Huang等[8]在实际功耗模型下,导出了多天线随机波束赋型系统能效和频效折中的近似关系式,并通过基站天线优化选择,在确定频效值的情况下得到了系统能效的优化值. Liu等[9]证明了下行正交频分复用(OFDM,orthogonal frequency division multiplexing)系统中,能效-频效的折中性能等价于系统总功耗的最小化及系统信道容量的最大化. Deng等[10]研究了上行多用户MIMO系统的能效和频效的最优的性能折中问题,将原始的非凸多目标优化问题转化为等价凸问题.
上述方法虽然从理论方面刻画了能效和频效的性能折中模型,但在实际变化场景中,针对高铁、动车等移动通信场景,并不能有效获取频效或能效特定需求下的优化指标.
基于此,在Massive-MIMO系统下行链路单小区多用户通信场景下,提出了一种频效和能效折中方法.通过构建能效和频效之间新的折中优化函数,将非凸的多目标问题转化为单目标的凸优化问题.并证明了该目标函数的优化问题的有效性等同于最大化传输速率并最小化系统功耗.仿真结果表明,提出的方法一方面能够在系统电路功耗确定的情况下,根据设定的能效值能够得到系统频效的最优值;另一方面,可以通过选择折中因子的参数值来改变系统能效或频效在系统中的权重,从而适应变化场景的传输需求.
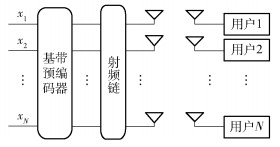
1 系统模型大规模多用户MIMO系统模型如图 1所示.考虑单小区多用户的下行传输场景,单小区基站配置M根天线,服务N个单天线用户,且满足M$\gg$N.
|
图 1 系统模型 |
假设基站发送信号矢量为x,第k个用户的接收信号矢量为
| $ {\mathit{\boldsymbol{y}}_k} = \sum\limits_{k = 1}^N {\sqrt {{p_k}} } \mathit{\boldsymbol{h}}_k^{\rm{H}}{\mathit{\boldsymbol{\omega }}_k}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{n}}_k} $ | (1) |
其中:xk为基站发送给第k个用户的信号矢量,且满足E{|xk|2}=1,其中1≤k≤N,E{·}表示求数学期望;hk为基站到用户k的信道增益矢量;ωk∈CM为用户k的加权矢量,pk为基站对用户k的发射功率;nk表示用户k端的噪声向量,服从复高斯分布,即CN(0, σ2).
若基站能够获取小区内所有用户完全的信道状态信息,并且考虑信道的空间相关性,系统信道矩阵可以表示为
| $ \mathit{\boldsymbol{G}} = {\mathit{\boldsymbol{D}}^{\frac{1}{2}}}\mathit{\boldsymbol{H}} $ | (2) |
其中:D=dig[β1, β2, …, βn]为大尺度衰落矩阵,βn=φε/dnξ表示路径损耗和阴影衰落,φ为包含载波频率和天线增益的常量,ε为服从10logε~N(0,σ2)分布的阴影衰落因子,dn为基站和用户n之间的距离,ξ为路径损耗因子.基站到所有用户的信道衰落矩阵为H=[h1, h2, …, hN]H,其中hk=[hk1, hk2, …, hkM]表示基站到用户k之间的信道增益矢量,且hij服从均值为0,方差为1的正态分布.
为了消除用户间的干扰,基站在信号发送前使用迫零预编码进行预处理,相应的迫零预编码矩阵为W=(G)†P1/2. P=dig(p1,p2, …, pN)为N个用户发射功率构建的对角矩阵.令(G)†=[g1, g2, …, gN],其中gn=[g1n, g2n, …, gMn]H,根据迫零预编码的性质有$\boldsymbol{h}_{i} \boldsymbol{g}_{j}\left\{\begin{array}{ll}=0, & i \neq j \\ \neq 0, & i=j\end{array}\right.$,因此第n个用户的信干噪比为
| $ {\gamma _n} = \frac{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}{p_n}}}{{B{n_0}}} $ | (3) |
其中:B为信号带宽,n0为噪声功率谱密度.因此,系统总的传输速率为
| $ {R_{{\rm{ total }}}} = \sum\limits_{n = 1}^N B {\rm{lb}} (1 + {\gamma _n}) $ | (4) |
相应的频效ηSE可以定义为
| $ {\eta _{{\rm{SE}}}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = \frac{{{R_{{\rm{ total }}}}}}{B} $ | (5) |
其中:ωk∈ω,Pk∈P分别表示用户加权矢量的集合{ωk}和发射功率的集合{pk},k=1, 2, …, N.
Massive MIMO系统的功率消耗主要由基站发射功率消耗和系统电路消耗2部分组成[11],相应可得系统的能效ηEE为
| $ \begin{array}{l} {\eta _{{\rm{EE}}}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = \frac{{{R_{{\rm{ total }}}}}}{{{P_{{\rm{ total }}}} + {P_{\rm{c}}}}} = \frac{{C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}}{{{P_{{\rm{ total }}}} + {P_{\rm{c}}}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{n = 1}^N {{R_n}} }}{{\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{{\rm{cm}}}}}} \end{array} $ | (6) |
其中Ptotal为发射功率,表示为
| $ {P_{{\rm{ total }}}} = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} $ | (7) |
pcm为每根天线的电路功率消耗,通常量化为常数处理,主要包括基带处理、传输滤波器、混频器、频率合成器和模数转换器中的功耗等,Pc为总的电路功率消耗.为了便于描述,这里将Rtotal记为C(ω, P).
2 能效和频效性能折中优化目标函数 2.1 构建优化目标函数为了便于分析能效和频效折中性能优化,受经济学中广泛应用的柯布-道格拉斯生产函数形式的启发[10],并利用加权和的方法引进折中系数δ,可将构建的函数表示为
| $ U = \delta \frac{{{\theta _{{\rm{EE}}}}}}{{{\eta _{{\rm{EE}}}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} + (1 - \delta )\frac{{{\theta _{{\rm{SE}}}}}}{{{\eta _{{\rm{SE}}}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} $ | (8) |
其中δ∈(0,1).将式(5)和式(6)代入式(8)可得
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} U = \delta \frac{{{\theta _{{\rm{EE}}}}}}{{{\eta _{{\rm{EE}}}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} + (1 - \delta )\frac{{{\theta _{{\rm{SE}}}}}}{{{\eta _{{\rm{SE}}}}(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} = \\ \delta \frac{{{\theta _{{\rm{EE}}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right)}}{{C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} + (1 - \delta )\frac{{{\theta _{{\rm{SE}}}}B}}{{C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} \end{array} $ | (9) |
其中θEE和θSE为归一化因子,其作用是使目标函数中的ηEE(ω, P)和ηSE(ω, P)具有相同的范围,取值由系统最大功率预算和平均CSI等参数决定.
由式(9)可知,所建立的函数关系式与用户加权矢量ω和发射功率P均有关,则优化目标函数可以表示为
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})} U(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = \delta \frac{{{\theta _{{\rm{EE}}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right)}}{{C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 - \delta )\frac{{{\theta _{{\rm{SE}}}}B}}{{C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1:\sum\limits_{n = 1}^N | {g_{mn}}{|^2}{p_n} \le \frac{{{p_{\rm{T}}}}}{M}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {2:B{\rm{lb}}\left( {1 + \frac{{{\beta _n}|{h_n}{g_n}{|^2}{p_n}}}{{B{n_0}}}} \right) \ge {R_{{\rm{t}},N}}}\\ {3:{p_n} \ge 0} \end{array} \end{array} $ | (10) |
其中:pT为基站的最大发射功率,Rt, N为满足第k个用户的最小传输速率.
2.2 优化目标函数的形式转换通过观察可以发现,式(10)是具有非凸非线性的分式形式,需要将其转化为满足系统传输速率最大化及功耗最小化的形式,才能进行优化目标的求解分析[12],即对应的形式为
| $ {\rm{min}}\{ {P_{\rm{t}}}, - {R_{{\rm{ total }}}}\} $ | (11) |
其中:Pt是系统总的功耗,包含发射功率消耗和电路功耗.基于此,系统能效和频效的多目标优化函数形式可表示为
| $ {\rm{min}}U = {\varphi _{{\rm{EE}}}}{P_{\rm{t}}} - {\varphi _{{\rm{SE}}}}{R_{{\rm{total}}}} $ | (12) |
其中φEE和φSE分别表示与Pt和Rtotal相关并令其二者在相同范围内的归一化因子.
接下来将对式(10)实施上述形式的转化分析.由于式(10)中对数函数C(ω, P)在(ω, P)上是严格的凸函数,所以,式(10)中的多目标函数可以提供完整的帕累托前沿(PF,pareto front),满足目标函数是拟凸或者其中至少一个函数是严格准凸的条件,即-qC(ω, P)[13].利用Dinkelbach[14]方法可以将式(10)中非凸非线性分式形式的目标函数转换为式(13)的等效凸函数,有
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})} U(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = \delta {\theta _{{\rm{EE}}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 - \delta ){\theta _{{\rm{SE}}}}B - qC(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ s}}{\rm{.t}}{\rm{. 1 \backsim 3}} \end{array} $ | (13) |
其中:q为一个能够使得式(10)在特定的δ下达到最小值的常数[14].
式(13)的资源分配优化问题可以通过Dinkelbach迭代方法在给定的δ下得到最优解[14].当δ=0时,该问题就转化为频效SE的最大化问题,此时,问题转变为常规的功率注水问题,不需要利用Dinkelbach迭代方法.为了更好地刻画该多目标优化问题的PF的曲线,除了在频效达到最大的点之外,必须在每个点上应用Dinkelbach迭代方法,所以必须对式(13)进一步简化.
由于式(13)中δ是给定的,所以(1-δ)θSEB是一个常数,忽略这个部分不会影响优化问题的解,且有δθEE>0,式(13)可以进一步改写为
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{min}}}\limits_{(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})} U(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = }\\ {\delta {\theta _{{\rm{EE}}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } g_{mn}^2{p_n} + M{p_{\rm{c}}}} \right) - qC(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = }\\ {\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right) - \frac{q}{{\delta {\theta _{{\rm{EE}}}}}}C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}\\ {{\rm{ s}}{\rm{.t}}{\rm{. 1 \backsim 3}}} \end{array} $ | (14) |
式(14)中的q/(δθEE)是一个大于零的常数,令(1-αEE)/αEE=q/θEE,0 < α < αEE < 1,将q/δθEE=(1-α)/α代入式(14)可以得到
| $ \begin{array}{*{20}{c}} {\mathop {{\rm{min}}}\limits_{(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})} U(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = }\\ {\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right) - \frac{{1 - \alpha }}{\alpha }C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}}) = }\\ {\alpha \left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right) - (1 - \alpha )C(\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{P}})}\\ {{\rm{ s}}{\rm{.t}}{\rm{. 1 \backsim 3}}} \end{array} $ | (15) |
分析式(15)可知,该优化问题旨在通过折中因子α使总功耗达到最小,同时使传输速率达到最大.式(15)表明,可以通过考虑系统总功率消耗的优化和特定加权因子范围(即0 < α < αEE)的频效来等效地刻画EE-SE优化后的帕累托曲线.
通过对比式(15)与式(12)可以发现,提出的优化目标等同于最大化传输速率,并最小化系统功耗,故而转换后的优化目标函数式(15)能有效地衡量Massive-MIMO系统能效和频效的折中性能.
3 优化目标函数求解 3.1 问题转化考虑多个用户的发射功率,系统的频效可以表示为
| $ C(\mathit{\boldsymbol{P}}) = \sum\limits_{n = 1}^N B {\rm{lb}} (1 + {\gamma _n}) $ | (16) |
此时,EE-SE折中优化目标函数可以表述为
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{P}} \frac{\alpha }{{{\theta _p}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right) - \frac{{(1 - \alpha )}}{{{\theta _{\rm{c}}}}}C(\mathit{\boldsymbol{P}}) $ | (17a) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n = 1}^N | {g_{mn}}{|^2}{p_n} \le \frac{{{p_{\rm{T}}}}}{M} $ | (17b) |
| $ {B{\rm{lb}}\left( {1 + \frac{{{\beta _n}|{h_n}{g_n}{|^2}{p_n}}}{{B{n_0}}}} \right) \ge {R_{{\rm{t}},N}}} $ | (17c) |
| $ {{p_n} \ge 0} $ | (17d) |
其中:θp和θc分别为功耗和传输速率的归一化因子,其大小主要由系统最大功率预算和平均CSI等参数决定.
通过观察,式(17)关于能效-频效折中优化问题转化为当α=0时,频效SE最大化;当α=1时,能耗最小,并且在α=αEE时能效取到有效解.此外,式(17)是一个减式规划问题求解,可以通过引理1进行转换.
通过观察式(17a)中的$\frac{\alpha}{\theta_{\mathrm{p}}}$($\sum\limits_{m=1}^{M} \sum\limits_{n=1}^{N}$|gmn|2pn+Mpc),可以知道其是关于pn的仿射函数,而-$\frac{(1-\alpha)}{\theta_{c}} C(\boldsymbol{P})$部分是关于pn的对数函数,所以其为凹函数.因此式(17a)是凹函数,而式(17b)(17c)(17d)是凸函数,根据文献[15]可知式(17)是凸优化问题.
对式(17)引入拉格朗日(Lagrangian)函数得到
| $ \begin{array}{*{20}{c}} {L(p,\lambda ,\mu ,\omega ) = \frac{\alpha }{{{\theta _p}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right) - }\\ {\frac{{(1 - \alpha )}}{{{\theta _{\rm{c}}}}}B {\rm{lb}} \left( {1 + \frac{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}{p_n}}}{{B{n_0}}}} \right) + }\\ {\sum\limits_{m = 1}^M {{\lambda _m}} \left( {\sum\limits_{n = 1}^N | {g_{mn}}{|^2}{p_n} - \frac{{{p_{\rm{T}}}}}{M}} \right) + }\\ {\sum\limits_{n = 1}^N {{\mu _n}} \left[ {{R_{{\rm{t}},N}} - B {\rm{lb}} \left( {1 + \frac{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}{p_n}}}{{B{n_0}}}} \right)} \right] + \sum\limits_{n = 1}^N {{\omega _n}} {p_n}} \end{array} $ | (18) |
其中:λm、μn和ωn均为引入的拉格朗日算子,且都大于零.令式(18)对Pn进行求导,并令其导数为零,即$\frac{\partial L(p, \mu, \omega, \lambda)}{\partial P_{n}}=0$,可以得到等式
| $ \begin{array}{*{20}{l}} {\left( {\frac{\alpha }{{{\theta _p}}}\sum\limits_{m = 1}^M | {g_{mn}}{|^2} - \frac{{(1 - \alpha )}}{{{\theta _{\rm{c}}}}}\frac{{B{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}}}{{(B{n_0} + {\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}{p_n}){\rm{ln}}2}}} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{m = 1}^M {{\lambda _m}} |{g_{mn}}{|^2} - \frac{{{\mu _n}B{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}}}{{(B{n_0} + {\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}{p_n}){\rm{ln}}2}} + {\omega _n} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\alpha }{{{\theta _p}}}\sum\limits_{m = 1}^M | {g_{mn}}{|^2} + \sum\limits_{m = 1}^M {{\lambda _m}} |{g_{mn}}{|^2} + {\omega _n} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{(1 - \alpha ){\mu _n} + {\theta _{\rm{c}}}}}{{{\theta _{\rm{c}}}}}\frac{{B{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}}}{{(B{n_0} + {\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}{p_n}){\rm{ln}}2}} = 0} \end{array} $ | (19) |
对式(19)进一步简化整理可以得到
| $ \begin{array}{l} {p_n} = \frac{{B(1 - \alpha - {\mu _n}{\theta _{\rm{c}}})}}{{{\theta _c}\left( {\frac{\alpha }{{{\theta _p}\sum\limits_{m = 1}^M | {g_{mn}}{|^2} + \sum\limits_{m = 1}^M {{\lambda _m}} |{g_{mn}}{|^2} + {\omega _n}){\rm{ln}}2}}} \right)}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{B{n_0}}}{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}}} \end{array} $ | (20) |
通过文献[16]可得到式(20)中拉格朗日算子的计算方法.
| $ \lambda _m^{(k + 1)} = {\left[ {\lambda _m^{(k)} - {\sigma _1}\left( {\frac{{{p_{\rm{T}}}}}{M} - \sum\limits_{n = 1}^N | {g_{mn}}{|^2}p_n^{(k)}} \right)} \right]^ + } $ | (21a) |
| $ {\mu _n^{(k + 1)} = {{[\mu _n^{(k)} - {\sigma _2}(r_n^{(k)} - {R_{T,N}})]}^ + }} $ | (21b) |
| $ {\omega _n^{(k + 1)} = {{[\omega _n^{(k)} - {\sigma _3}p_n^{(k)}]}^ + }} $ | (21c) |
其中:[x]+=max {0, x},k表示迭代次数,σ1、σ2以及σ3表示迭代步长,并且都大于零.
至此,式(10)关于能效-频效折中的非凸多目标问题转化为凸优化的单目标问题.目标函数的最优解可以通过pn的迭代方式得到.
3.2 优化算法根据以上分析可以知道,式(17)的优化问题转化为凸优化的问题,观察式(20)的结构,利用拉格朗日乘子法进行变换,并采用功率迭代求解算法进行最优化求解,迭代算法1如下:
步骤1 初始化参数[16]:λm(0),ωn(0),μn(0),pn(0),q(0);
步骤2 计算
| $ \begin{array}{*{20}{c}} {p_n^{(k + 1)} = }\\ {\frac{{B(1 - \alpha - \mu _n^{(k)}{\theta _c})}}{{{\theta _{\rm{c}}}\left( {\frac{\alpha }{{{\theta _{\rm{p}}}}}\sum\limits_{m = 1}^M | {g_{mn}}{|^2} + \sum\limits_{m = 1}^M {\lambda _m^{(k)}} |{g_{mn}}{|^2} + \omega _n^{(k)}} \right){\rm{ln}}2}} - }\\ {\frac{{B{n_0}}}{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}}}} \end{array} $ |
根据式(21a)、式(21b)和式(21c)更新拉格朗日算子λm(k+1),μn(k+1)和ωn(k+1)以及更新功率
| $ \begin{array}{*{20}{c}} {p_n^{(k + 1)} = }\\ {\frac{{B(1 - \alpha - \mu _n^{(k + 1)}{\theta _{\rm{c}}})}}{{{\theta _{\rm{c}}}\left( {\frac{\alpha }{{{\theta _{\rm{p}}}}}\sum\limits_{m = 1}^M | {g_{mn}}{|^2} + \sum\limits_{m = 1}^M {\lambda _m^{(k)}} |{g_{mn}}{|^2} + \omega _n^{(k)}} \right){\rm{ln}}2}} - }\\ {\frac{{B{n_0}}}{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}}}}\\ {k = k + 1} \end{array} $ |
步骤3 若
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {\frac{\alpha }{{{\theta _p}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}p_n^{(k)} + M{p_{\rm{c}}}} \right) - } \right.\\ \left. {\frac{{(1 - \alpha )}}{{{\theta _{\rm{c}}}}}B {\rm{lb}} \left( {1 + \frac{{{\beta _n}|{\mathit{\boldsymbol{h}}_n}{\mathit{\boldsymbol{g}}_n}{|^2}p_n^{(k)}}}{{B{n_0}}}} \right)} \right| \ge \tau \end{array} $ |
停止迭代,输出pn,k;
步骤4 Else跳转到步骤2.
通过迭代算法1,计算到当α=αEE时,能效取得优值,在这种情况下,提出算法2对系统能效的最优值进行迭代求解,并找到其对应的αEE使其满足L(pn, αEE)=0,迭代算法2如下:
步骤1 输入αinitial, ξ;
步骤2 设置αEE=αinitial;
步骤3 While F(PEE, n) < -ξ do
步骤4 通过算法1计算出PEE, n
步骤5 计算
| $ {\alpha _{{\rm{EE}}}} = \frac{{{\theta _{\rm{p}}}C({P_{{\rm{EE}},n}})}}{{{\theta _{\rm{c}}}\left[ {\frac{\alpha }{{{\theta _{\rm{p}}}}}\left( {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N | } {g_{mn}}{|^2}{p_n} + M{p_{\rm{c}}}} \right)} \right] + {\theta _{\rm{p}}}C({P_{{\rm{EE}},n}})}} $ |
然后更新L(PEE, n)
End while
步骤6 输出PEE, n和αEE.
上述算法中,步骤4的复杂度为O[Nlb(Δλ/τ)],所以算法2的复杂度为O[NαEENlb(Δλ/τ)],其中Δλ表示算法1中λ的终止值与初始值之差,NαEE表示计算出αEE时,所需的迭代次数.当折中因子α=αEE时,通过以上所提算法,可以得到能效最优值,从而进一步得到在该能效参数值下频效的参数值.
4 仿真结果分析下面通过仿真来分析所提出的MIMO系统EE-SE折中多目标优化问题.仿真环境设置如下:假设基站与用户都拥有完全的信道状态信息,基站位于小区的中心位置,用户均匀分布在小区内.基站采用ULA发射天线阵列,迭代停止范围参数τ为0.01,基站在发送信号前使用迫零预编码进行预处理.仿真参数的设置如表 1所示.
|
|
表 1 仿真参数设置 |
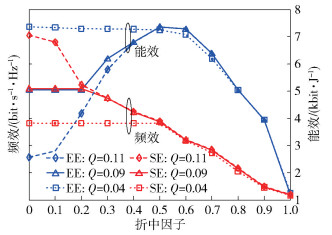
图 2为发射天线128,有效功率预算Q=PT/θp分别为0.04,0.09,0.11时[17],SE和EE在不同权衡因子α下的性能曲线.从图 2可以看出:①当α=0时,该问题转变为最大化系统频效SE,当α=1时,问题转变为最小化传输功率;②当α=αEE=0.5,系统平均能效EE达到了最大,当α从0~αEE变化时,EE在逐渐增大,而SE在逐渐减小,且当α从αEE~1变化时,EE和SE都在减小,故而此时性能折中点为αEE=0.5.在图 2中,可通过改变α来实现预定的EE或SE的性能指标;③对于在较大的发射功率预算(Q=0.11)处,可以观察到SE和EE与α之间存在的折中关系,可以通过设定能效值得到该设定目标下频效所能达到的最优值;反之亦然.此外,足够的传输功率预算限制了SE随着α的减小而改善的趋势,并且对EE的曲线从其所预期的趋势进行了限制.
|
图 2 不同权衡因子下的能效和频效的比较 |
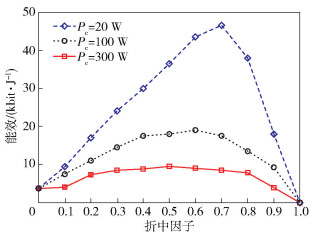
图 3所示为Q=PT/θp=0.11时,不同电路功率消耗对于系统EE的作用曲线.可以看出:①随着电路功耗Pc的降低,系统EE在增大,这是因为传输数据的总功耗成本降低,符合式(6)的变化趋势. ② Pc为20、100、300 W时,系统EE的最大值出现在αEE为0.7、0.6、0.5处,这显示出随着αEE的增加,Pc在降低,说明了传输系统在Pc较大时,会用较大的传输功率去保证数据传输的成功,并提高EE;反之,在Pc较小时,用较小的传输功率提高EE.
|
图 3 不同电路功耗下的系统能效性能 |
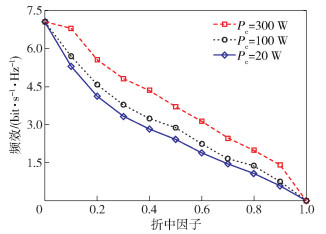
图 4所示为Q=PT/θp=0.11时,不同电路功率消耗对于系统SE的作用曲线.可以看出:①对于α=0时,优化问题转变为最大化系统SE,并且无论Pc的值如何变化,都得到了相等的最大SE,这是因为SE不依赖于电路功耗;②对于α>0时,随着电路功耗Pc的增加,系统SE在增大,这种趋势与系统EE的变化是相反的,符合二者的矛盾关系.综合考虑,所提方案在不同场景要求上,具有良好的适应性和较好的系统性能.
|
图 4 不同电路功耗下的系统频效性能 |
在MIMO系统中,当发射功率远大于电路功率时,能效和频效是相互制约的关系,二者存在性能折中的优化问题.基于此,提出了基于多目标优化的EE-SE折中方案.通过构建能效和频效之间新的折中优化函数关系,将非凸的多目标问题转化为凸优化的单目标问题,进而利用拉格朗日乘子法得到能效的最优解,并根据设定的折中因子值,进一步得到该能效值所对应的频效参数值.仿真结果表明,所提方案能够在设定的不同能效值下实现对频效的优化,并通过改变折中因子的大小对频效和能效在系统中的权重进行实时动态调整,从而适应不同的传输场景需求.
| [1] |
Ribeiro L N, Schwarz S, Rupp M, et al. Energy efficiency of mmWave massive MIMO precoding with low-resolution DACs[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(2): 298-312. DOI:10.1109/JSTSP.2018.2824762 |
| [2] |
Bhatt M K, Sedani B S, Parmar K R. Achievable uplink capacity with linear detectors and tradeoff between spectral efficiency and energy efficiency for massive MIMO system[J]. i-Manager's Journal on Communication Engineering and Systems, 2018, 7(2): 26. DOI:10.26634/jcs.7.2.14440 |
| [3] |
Ding Jupeng, Wang Kun, Xu Zhengyuan. Impact of different LED-spacing in arrayed LED transmitter on VLC channel modeling[C]//2014 Sixth International Conference on Wireless Communications and Signal Processing(WCSP). Hefei: [s.n.], 2014: 1-6.
|
| [4] |
Zhang Rui, Li Yongzhao, Wang Chengxiang, et al. Energy-spectral efficiency trade-off in underlaying mobile D2D communications:an economic efficiency perspective[J]. IEEE Transactions on Wireless Communications, 2018, 7(17): 4288-4301. |
| [5] |
Ngo H Q, Larsson E G, Marzetta T L. Energy and spectral efficiency of very large multiuser MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(4): 1436-1449. DOI:10.1109/TCOMM.2013.020413.110848 |
| [6] |
Onireti O, Héliot F, Imran M A. Closed-form approximation for the trade-off between energy efficiency and spectral efficiency in the uplink of cellular network[C]//17th European Wireless 2011-Sustainable Wireless Technologies.[S.l.]: VDE, 2011: 1-6.
|
| [7] |
Héliot F, Imran M A, Tafazolli R. On the energy efficiency-spectral efficiency trade-off over the MIMO rayleigh fading channel[J]. IEEE Transactions on Communications, 2012, 60(5): 1345-1356. DOI:10.1109/TCOMM.2012.031712.110215 |
| [8] |
Huang Yi, Qiu Ling. On the energy efficiency-spectral efficiency tradeoff in random beamforming[J]. IEEE Wireless Communications Letters, 2014, 3(5): 461-464. DOI:10.1109/LWC.2014.2339219 |
| [9] |
Liu Fei, Yang Qinghai, He Qingsu, et al. Energy efficiency and spectral efficiency tradeoff in downlink OFDMA systems with imperfect CSI[J]. AEU-International Journal of Electronics and Communications, 2017, 85: 54-58. |
| [10] |
Deng Lei, Zhang Wenjie, Rui Yun, et al. Utility maximization for uplink MU-MIMO: combining spectral-energy efficiency and fairness[C]//2016 European Conference on Networks and Communications (EuCNC).[S.l.]: IEEE, 2016: 79-83.
|
| [11] |
Huang Yongming, He Shiwen, Wang Jiaheng, et al. Spectral and energy efficiency tradeoff for massive MIMO[J]. IEEE Transactions on Vehicular Technology, 2018, 67(8): 6991-7002. DOI:10.1109/TVT.2018.2824311 |
| [12] |
Song Zhengyu, Ni Qiang, Sun Xin. Spectrum and energy efficient resource allocation with QoS requirements for hybrid MC-NOMA 5G systems[J]. IEEE Access, 2018, 6: 37055-37069. DOI:10.1109/ACCESS.2018.2851609 |
| [13] |
Branke, Jürgen. Multiobjective optimization:interactive and evolutionary approaches[M]. Berlin: Springer Science & Business Media, 2008.
|
| [14] |
Sun Y, Ng D W K, Ding Z, et al. Optimal joint power and subcarrier allocation for full-duplex multicarrier non-orthogonal multiple access systems[J]. IEEE Transactions on Communications, 2017, 65(3): 1077-1091. DOI:10.1109/TCOMM.2017.2650992 |
| [15] |
Bo yd, Vandenberghe, Faybusovich. Convex optimization[J]. IEEE Transactions on Automatic Control, 2006, 51(11): 1859-1859. DOI:10.1109/TAC.2006.884922 |
| [16] |
Ng D W K, Lo E S, Schober R. Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas[J]. IEEE Transactions on Wireless Communications, 2012, 11(9): 3292-3304. DOI:10.1109/TWC.2012.072512.111850 |
| [17] |
Deruyck M, Tanghe E, Joseph W, et al. Model for power consumption of wireless access networks[J]. IET Science Measurement & Technology, 2011, 5(4): 155-161. |


