We consider the wireless senor network which is equipped with an energy harvesting device and a rechargeable battery, and the aim is to enable the sensor having the ability of adaptively adjusting the data sampling rate according to the available energy. Since the stochastic nature of the harvested energy, we define the energy deficiency probability for equivalently characterizing an information acquisition metric. We formulate the problem of adjusting data sampling rate as a constrained optimization problem, maximizing the data sampling rate while keeping the energy deficiency probability below a threshold. The classic large deviation theory is invoked for estimating the energy deficiency probability. Our experimental results verify that the algorithms proposed have the adaptation capability to accommodate both the energy-dynamics and the channel-dynamics for improving the information acquisition.
针对具有能量捕获装置以及可充电电池的无线传感网,为了使无线传感器具有根据可用能量自适应调整数据采样速率的能力,所获得的能量具有随机性,定义了可等价表示信息获取度量的能量不足概率.将调节数据采样速率的问题定义为约束优化问题,使数据采样速率最大化,同时将能量不足概率保持在阈值以下.利用经典的大偏差理论估计能量不足概率.实验结果表明,所提出的算法具有自适应能力,既能适应能量动态变化,又能适应信道动态变化,提高了信息采集效率.
In recent years, the energy harvesting(EH) technology is leading to significant interests in systems powered by harvested ambient energy. In contrast to traditional systems powered by battery, using energy from nature not only reduces the carbon emission but also sustains device equipped with a rechargeable battery with an infinite lifetime. However, the intermittent and stochastic nature of the harvested energy put forward a fundamental challenge when applying EH technique. Hence, in this paper, we propose an adaptive policy for adjusting data sampling rate to maximize the effective information in wireless sensor application.
The application ofEH technology in wireless sensor network has attracted substantial research attention, especially to seek novel EH scheduling policies for improving the system performance. To mitigate efficiency loss of workload, Ref. [1] proposed an architecture to achieve maximum energy efficiency tracking for the overall sensor node. In Ref. [2], the authors studied the properties of the conditional expected rewards and further presented a sub-optimal threshold-based transmission scheduling policy for EH sensors nodes through maximizing the conditional expected rewards with respect to data storage and energy storage, respectively. By using virtual queues and techniques from Lyapunov optimization, Ref. [3] formulated a long-term time-averaged joint scheduling and sensing allocation problem in wireless sensor networks with finite energy and data buffers. Based on realistic energy and network models, the authors of Ref. [4] incorporated CPU-intensive edge operations with sensing and networking to jointly optimize EH wireless sensor network performance. Further, a MIMO network control system with an EH sensor was considered in Ref. [5], and MIMO precoding was designed at the sensor so as to stabilize the unstable dynamic plant. The work in Ref. [6] proposed a two-stage water filling policy to achieve throughput maximization in EH and power grid coexisting wireless communication systems. In Ref. [7], the power-delay tradeoff is formulated as a stochastic optimization problem, and solved by Lyapunov optimization technique. The scenario that one user harvests energy from an energy access point to power its information transmission to a data access point is investigated in Ref. [8]. It should be noted that the works mentioned above focus on the energy efficiency optimization. But currently the EH technology offers only a small amount of energy storage and is capable of harvesting only a trivial amount of energy. Therefore, new technique for managing the energy associated with sensor node is required.
In this paper, we focus on the estimation of energy deficiency probability (EDP) for characterizing the degree of matching between the energy demand and the harvested energy. We employ thelarge deviation theory(LDT) to formulate a model for estimating the EDP, which is applied to assist the sensor in promptly controlling the data sampling rate. The proposed method relies on online measurements instead of any prior statistical knowledge of the harvested energy and the channel state. The main contributions of this paper are summarized as follows:
1) We transform the requirement of information efficiency into the energy deficiency which is kept lower than a desired level. Accordingly, the problem of adjusting data sampling rate overEH aided wireless sensor system is formulated as maximizing the sampling rate subject to a constraint imposed on the EDP in order to guarantee high information efficiency.
2) An EDP estimation model based onLDT is proposed by monitoring the energy-buffer fullness and its variations in the rechargeable battery. By applying LDT, this model accurately characterizes the probability of the rare events of energy deficiency, which assist the sensor in controlling the data sampling rate.
3) We conduct numerical simulations for demonstrating the effectiveness of the proposeddata sampling rate adjustment algorithm. Q-learning, a greedy algorithm is implemented as our benchmark algorithms. The simulation results show that the proposed method achieves an improved performance.
The rest of this paper is organized as follows. Section1 describes the system model and formulates the data sampling rate adjustment problem. In Section 2, we propose the EDP estimation method based on the LDT. Section 3 derives the online measurement based adaptive data sampling rate adjustment algorithm based on the EDP estimation model. Our simulation results and performance analysis are presented in Section 4. Finally, the conclusions are offered in Section 5.
1 System modelWe consider a wireless sensor equipped with an EH device and a rechargeable battery having a limited capacity, as depicted in Fig. 1. The device can collect natural renewable energy from the ambience and store in the battery. By utilizing the observations of the energy-buffer fullness and its variations in the rechargeable battery, the prediction calculator estimates the EDP for instructing the decision-maker to generate the data sampler commands. The data sampler executes the data sampling and forms a data stream to control panel.
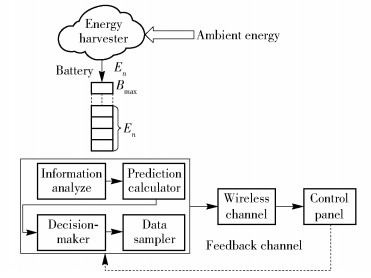
|
Figure 1 System architecture for sensor wireless communication |
We assume that this wireless sensor operates in a time-slotted fashion which means the time is divided into slots of equal duration and normalized to unity. At the beginning of each time slot, the decision-maker makes the data sampling rate command to control the data sampler based on the battery level. Let Rn be the data sampling rate made by decision-maker at time slot n. Rn∈{R0, R1, …, Rmax} characterize the sensor operation level. Higher Rn, implies more precise information will transmit to control panel. Correspondingly, the size of data that should be delivered is given by:
| $ {D_n} = f\left( {{R_n}} \right) $ | (1) |
Where f(·) indicates the relationship between the data sampling rate and data size. The wireless channel is assumed to be constant over a slot duration, but it changes at the slot boundaries. Let N0 be the white Gaussian noise and W the wireless band width, according to Shannon's capacity formula, the amount of transmission power in the th time slot is
| $ {P_n} = \frac{W}{{{N_0}{H_n}}}\left( {{2^{\frac{{{D_n}}}{{dW}} - 1}}} \right) $ | (2) |
where Hn is the channel state and d is the duration of a slot.
Since the channel state Hn and the amount Dn of the data are available for transmission during the time slot n, the amount of energy Ent required to transmit Dn bits is calculated as:
| $ E_n^{\rm{t}} = P\left( {{H_n}, {D_n}} \right)d $ | (3) |
Let Enh∈ε={0, 1, …, emax} denote the amount of energy harvested in the nth time slot. The process Enh is assumed to be an i.i.d random variable. Let Bn represent the energy stored in the battery at the beginning of the nth time slot, and the capacity of the battery is Bmax. The energy Enh harvested in the nth slot, is available until the beginning of the (n+1)th slot. Hence, the dynamics of the energy in the battery are characterized by
| $ {B_{n + 1}} = {B_n} - E_n^{\rm{t}} + E_n^{\rm{h}}, n = \{ 1, 2, \cdots \} $ | (4) |
For sensor operation, the data transmission interruptions substantially reduce the precision of information. Hence, it is desired that the battery always holds sufficient energy for transmitting data of the forthcoming time slots in order to avoid transmission interruptions. Motivated by this, we define a low threshold of Bmin as an indicator of the battery being partially depleted. In order to characterize the energy deficiency, we define the EDP as
| $ {p_{{\rm{ED}}}} = P\left( {B < {B_{\min }}} \right) $ | (5) |
where B is a random variable representing the energy-buffer fullness. Higher EDP, pED, implies a lower energy fullness in the near future, hence energy deficiency is more likely to occur.
In order to achieve a more accurate data service, the EDP should be kept low. Hence, the data transmission problem in wireless sensor system is interpreted as that of choosing the maximumdata sampling rate for maximizing the information precision subject to a given EDP, which can be formulated as
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{_{{R_n} \in \{ 1, 2, \cdots , N\} }} {R_n}}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}P\left( {B < {B_{\min }}} \right){p_{{\rm{SIR}}}}} \end{array} $ | (6) |
where pSIR is a given threshold value of sufferable interrupt rate. In this optimization problem, we transform the transmission interruptions into a probability constraint that the EDP is kept below a certain tolerable level. Different values of pSIR correspond to different SIR levels.
2 Estimation model of energy deficiency probabilityWe assume that the index of the current time slot is n, and the current battery level is Bn, while Rn represents the data sampling rate during the time slot. We predict the EDP at the (n+N)th (N > 0) slot under the condition of supporting the data sampling rate Rn in the future N time slots. Let PESn+N denote the EDP at the (n+N)th slot, which is defined as
| $ P_{{\rm{ES}}}^{n + N} = P\left( {{B_{n + N}} < {B_{\min }}} \right) $ | (7) |
where N is the length of the prediction interval.
2.1 Reinterpretation of energy deficiency probabilityFor a given time slot k, the reduction of the energy available for the transmitter is characterized by
| $ \Delta {E_k} = E_k^{\rm{t}} - E_k^{\rm{h}} $ | (8) |
where ΔEk∈{-emaxh, …, 0, 1, …, etmax}. Let πi=P(ΔEk=i) enote the probability that the energy reduction of the battery is ΔEk=i. Since Etk is the energy consumed in the kth slot and Ekh is the energy collected in the kth slot, the difference ΔEk characterizes the instantaneous energy mismatch between the energy required for keeping Rn data sampling rate and the harvested energy.
The total reduction of the energy in the rechargeable battery during the period spanning from the nth slot to the (n+N)th slot is characterized as
| $ \Delta {E^{n + N}} = \sum\limits_{i = 1}^N \Delta {E_{n + i}} $ | (9) |
Then, the energy-buffer fullness Bn+N in the (n+N)th time slot is given as
| $ {B_{n + N}} = {B_n} - \Delta {E^{n + N}} $ | (10) |
According to Eq.(7), the EDP at the (n+N)th slot is rewritten as
| $ P_{{\rm{ES}}}^{n + N} = P\left( {{B_n} - \Delta {E^{n + N}} < {B_{\min }}} \right) $ | (11) |
We define the maximum tolerable average energy reduction during each of the forthcoming N slots as
| $ {a_{{\rm{ES}}}} = \frac{{{B_n} - {B_{\min }}}}{N} $ | (12) |
and the expected value of the average reduction of the energy fullness in the battery in each slot during the future n slots as
| $ {m_{{\rm{ES}}}} = E\left[ {\frac{{\sum\limits_{i = 1}^N \Delta {E_{n + i}}}}{N}} \right] $ | (13) |
where E[·] denotes the expectation operator. Furthermore, mES≥aES implies while keeping the current data sampling rate, after the forthcoming N slots, transmission interruption will definitely occur.
Let us rewrite Eq.(11) as
| $ \begin{array}{*{20}{c}} {P_{{\rm{ES}}}^{n + N} = P\left( {{B_n} - \Delta {E^{n + N}} < {B_{\min }}} \right) = }\\ {P\left( {\frac{{\Delta {E^{n + N}}}}{N} > \frac{{{B_n} - {B_{\min }}}}{N}} \right) = }\\ {P\left( {\frac{{\sum\limits_{i = 1}^N \Delta {E_{n + i}}}}{N} > {a_{{\rm{ES}}}}} \right)} \end{array} $ | (14) |
The term
Since our objective is to provide an interruption-free data transmission, the occurrences of the transmission interruption are expected to be rare events. According to Ref. [9], the LDT can be employed to estimate the probability of rare or tail events. Hence, Cramér's theorem applied in the context of the LDT constitutes an appropriate method of estimating the EDP in Eq.(7).
According to Cramér's theorem[10], the sequence ΔEi(i=1, 2, …) obeys the LDT which is rewritten as
| $ \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\log P\left( {\frac{1}{N}\sum\limits_{i = 1}^N {{R_i}} > a} \right) = - I(a) $ | (15) |
where the function I(a) is referred to as the "rate function". Therefore, if aES > mES, we have
| $ \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\log P\left( {\frac{1}{N}\sum\limits_{i = 1}^N \Delta {E_{n + i}} > {a_{{\rm{ES}}}}} \right) = - I\left( {{a_{{\rm{ES}}}}} \right) $ | (16) |
where
| $ I\left( {{a_{{\rm{ES}}}}} \right) = \mathop {\sup }\limits_{\theta > 0} \left\{ {{a_{ES}}\theta - \log M(\theta )} \right\} $ | (17) |
and
| $ \log M(\theta ) = \log \left\{ {\sum\limits_{i = - e_{\max }^{\rm{h}}}^{\theta _{\max }^{\rm{t}}} {{\pi _i}} \exp [i\theta ]} \right\} $ | (18) |
The rate function I(aES) is usually referred as the Fenchel-Legendre transform or convex conjugate[9]. Note that both logM(θ) and the rate function I(aES) are convex[9].
Since Eq.(16) is logarithmically asymptotic, for a sufficiently large N, the EDP of the (n+N)th slot can be approximated by
| $ P_{{\rm{ES}}}^{n + N} \approx \exp \left[ { - NI\left( {{a_{{\rm{ES}}}}} \right)} \right] $ | (19) |
Owning to the rapid exponential decay of the EDP estimate with N, a moderate value of N can be used to acquire an accurate EDP estimate.
2.3 Online estimation of energy deficiency probabilityIn order to estimate the EDP according to Eq.(19), aES, mES, πi are required. It is straightforward to calculate aES according to Eq.(12). However, because of the absence of any prior knowledge about the probability distribution of ΔEk, it remains an open challenge to derive analytical expressions for mES and πi. Consequently, we have to utilize historical observations for estimating these parameters by invoking a sliding window-based method.
Let us denote the observed sequence of the energy fullness decrements in the battery by ΔE1, ΔE2, ΔE3, …. The sliding window covers the Ns most recent entries in this sequence, which is slid over this sequence. For the nth window, the observation vector is denoted by Wn=[ΔEn, ΔEn-1, …, ΔEn-Ns+1].
The parameter mES can be approximated by the sample mean of the observation vector Wn, yielding
| $ {{\hat m}_{{\rm{ES}}}} = \frac{{\sum\limits_{i = n - {N_s} + 1}^n \Delta {E_i}}}{{{N_s}}} $ | (20) |
For the parameter πi, i∈{-ehmax, …, 0, 1, …, eTmax}, we propose the following estimation technique.
Let Ni denote the number of ΔEk=i events happening within the sliding window, which is counted by
| $ {N_i} = \sum\limits_{k = n - {N_s} + 1}^n {{I_{\left\{ i \right\}}}} \left( {\Delta {E_k}} \right) $ | (21) |
where
| $ {I_{\left\{ i \right\}}}\left( {\Delta {E_k}} \right) = \left\{ {\begin{array}{*{20}{l}} {1, }&{{\rm{ if }}\Delta {E_k} = i}\\ {0, }&{{\rm{ otherwise }}} \end{array}} \right. $ | (22) |
is an indicator function. Then, the frequency of ΔEk=i can be estimated as
| $ {{\hat q}_i}(n) = \frac{{{N_i}}}{{{N_s}}} $ | (23) |
Having too small an Ns may result in an excessive estimation error of
Although
| $ {{\hat \pi }_i}(n) = \rho {{\hat \pi }_{i - 1}} + (1 - \rho ){{\hat q}_i}(n) $ | (24) |
where the forgetting parameter ρ∈[0, 1] controls the weighting of historical estimates. This smoothening method is especially useful in a non-stationary environment. If ρ approaches 1, the current estimate
In this section, we will discuss the details of our online measurement-based algorithm conceived for data sampling rate adjustment, which invokes the online EDP estimation model of Section2 for finding the highest data sampling rate under our SIR constraint. The problem(6) that maximizes the data sampling rate in the th slot can be solved according to:
| $ \left. {\begin{array}{*{20}{l}} {P\left( {{B_n} - E_n^{\rm{t}}\left( {{R_n}} \right) + E_n^{\rm{h}} < {B_{\min }}} \right){p_{{\rm{SIR}}}}}\\ {P\left( {{B_n} - E_n^{\rm{t}}\left( {{R_n} + 1} \right) + E_n^{\rm{h}} < {B_{\min }}} \right){p_{{\rm{SIF}}}}} \end{array}} \right\} $ | (25) |
where En(Rn) denotes the energy allocated for transmitting the data with Rn data sampling rate. Since the current data sampling rate is Rn, the sequence Etn(Rn+1) is not observable. Hence, the EDP in the second inequality of Eq.(25) cannot be directly calculated according to the steps of Section 2.3. Here, we consider a heuristic iteration policy for solving Eq.(25). The basic idea is to constrain the data sampling rate adjustments to a single level, yielding Rn∈{Rn-1, Rn, Rn+1}.
For the case of
| $ {R_{n + 1}} = \max \left( {{R_n} - 1, {R_0}} \right) $ | (26) |
By contrast, for the case of
According to the estimation model of Section 2, the EDP in the (n+N)th slot can be approximated as
| $ \hat P_{{\rm{ES}}}^{n + N} = \exp \left[ { - NI\left( {{a_{{\rm{ES}}}}} \right)} \right] $ | (27) |
Thus, the EDP
Based on the above discussions, the proposedonline measurement-based adaptive data sampling (OM-ADS) is summarized in Algorithm 1.
Algorithm 1 OM-ADS
Data: the historical observations: Bi, Eit, and Eih
(i={1, 2, …, n}); the data sampling rate in the nth slot: Rn;
the desired SIR level: pSIR; the SIR threshold PT; a given constant KT; a temporary counter K.
While true do
Calculate
if
jn+1←jn-1
else
Calculate
2.3.
if
jn+1←jn-1
else
if
K←K+1
if K≥Kt then
jn+1←jn+1
K←0
end
end
end
end
end
4 Experimental resultsIn this section, we carried out a series of experiments for evaluating the performance of the proposed methods. In order to quantify the attainable performance improvements, we also implemented a heuristic greedy method, an online Q-learning method[12] as benchmark algorithms.
We consider a nondispersive Rayleigh fading channel with bandwidth w=2 MHz and noise spectral density of N0=4×10-9 W/Hz. The amount of the energy harvested is assumed to follow the Poisson distribution. We also consider different data sampling rates for different data transfers. In order to characterize the capability of adaptive data sampling rates, we set the harvest energy, varying expectations from 0.2 to 1.6 with the step size of 0.2. The amount of the energy harvested is assumed to follow the Poisson distribution.
For the proposed OM-ADS, the parameters were set as follows: the length of sliding window was Ns=110, the size of prediction interval was N=50, the forgetting parameter was ρ=0.7, the desired EDP level was PSIR=0.001 and the low threshold value was PT=0.1×PSIR. For the Q-learning method, we follow to set the learning rate and the discount factor to 1 and 0.8, respectively.
Fig. 2(a) characterizes different data sampling rates versus the average energy harvest rate, while Fig. 2(b) characterizes the transmission interruption rates that reflect the integrity of data collection versus the average energy harvest rate. It can be observed that although the greedy method performs better than the other methods in terms of data sampling rates, it suffers from a higher transmission interruption rate, especially in situation of low energy harvest rate. This is because the greedy method maximizes the data sampling rate according to the current available energy in the battery, it frequently suffers from energy scarcity, which lead to the highest transmission interruption rate, thus reducing the integrity of the sampled data. This implies that excessive data collection may result in energy insufficient in the future. Similarly, as the Q-learning method merely aims for maximizing the system's throughput by adjusting the data sampling rate according to the system's state, but without considering energy storage. This implies that excessive data collection may result in energy insufficient in the future. The proposed OM-ADS method achieves a slightly worse data sampling rate, but it gains a much lower transmission interruption rate. The reason for this trend is that the OM-ADS benefits from evaluating the energy shortage probability of the forthcoming slot in each time slot for prudently adjusting data sampling rate for keeping the likelihood of energy shortage under a certain tolerance level.
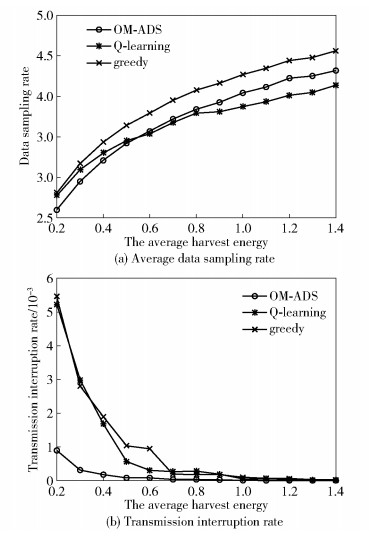
|
Figure 2 Performance comparison for different energy harvesting rates |
We also can see that as the capture energy increases, thedata sampling rate of each algorithm increases and the probability of transmission interruption is reduced, and it meets our expectations.
5 ConclusionsIn this paper, we discussed the SIR-guaranteed adaptive data sampling rate adjustment in wireless sensor network. The SIR constraint is interpreted as keeping the energy deficiency probability below a given threshold, in order to reduce the rate of transmission interruptions that substantially reduce the information efficiency. Large deviation theory was invoked for estimating the EDP via online measurements. A heuristic method, OM-ADS, was proposed based on the EDP estimation to maximize the information efficiency associated with the EDP constraint. The experimental results demonstrated that the proposed adaptive data sampling rate adjustment methods is capable of effectively improving the information efficiency while keeping the energy available for the future.
| [1] |
Sun Yinan, Yuan Zhe, Liu Yongpan, et al. Maximum energy efficiency tracking circuits for converter-less energy harvesting sensor nodes[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2017, 64(6): 670-674. doi: 10.1109/TCSII.2016.2623354 |
| [2] |
Huang Liang, Bi Suzhi, Qian Liping. Optimal threshold-based transmission scheduling policy for energy harvesting sensor nodes[C]//2016 IEEE Global Communications Conference. New York: IEEE Press, 2016: 1-6.
|
| [3] |
Sunny A. Joint scheduling and sensing allocation in energy harvesting sensor networks with fusion centers[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3577-3589. doi: 10.1109/JSAC.2016.2611962 |
| [4] |
Yang Shusen, Tahir Y, Chen P Y, et al. Distributed optimization in energy harvesting sensor networks with dynamic in-network data processing[C]//The 35th Annual IEEE International Conference on Computer Communications. New York: IEEE Press, 2016: 1-9.
|
| [5] |
Cai Songfu, Lau V K N. MIMO precoding for networked control systems with energy harvesting sensors[J]. IEEE Transactions on Signal Processing, 2016, 64(17): 4469-4478. doi: 10.1109/TSP.2016.2568158 |
| [6] |
Gong Jie, Zhou Sheng, Niu Zhisheng. Optimal power allocation for energy harvesting and power grid coexisting wireless communication systems[J]. IEEE Transactions on Communications, 2013, 61(7): 3040-3049. doi: 10.1109/TCOMM.2013.05301313.120705 |
| [7] |
Yang Jian, Yang Qinghai, Kwak K S, et al. Power-delay tradeoff in wireless powered communication networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(4): 3280-3292. doi: 10.1109/TVT.2016.2587101 |
| [8] |
Zhou Xun, Ho C K, Zhang Rui. Wireless power meets energy harvesting:a joint energy allocation approach in OFDM-based system[J]. IEEE Transactions on Wireless Communications, 2016, 15(5): 3481-3491. doi: 10.1109/TWC.2016.2522410 |
| [9] |
Mandjes M. Large deviations for Gaussian queues:modeling communication networks[M]. Hoboken: Wiley, 2007: 25.
|
| [10] |
Gardner E S. Exponential smoothing:the state of the art-Part Ⅱ[J]. International Journal of Forecasting, 2006, 22(4): 637-666. doi: 10.1016/j.ijforecast.2006.03.005 |
| [11] |
Blasco P, Gunduz D, Dohler M. A learning theoretic approach to energy harvesting communication system optimization[J]. IEEE Transactions on Wireless Communications, 2013, 12(4): 1872-1882. doi: 10.1109/TWC.2013.030413.121120 |


