为解决反馈型两级交换结构(FTSA)对调度算法的时间限制问题,提出了一种脉动反馈型两级交换结构(PFTSA).PFTSA将调度算法所需信息以脉动的形式反馈至输入端口,通过预处理机制使调度算法获得目标缓存的准确信息,从而避免信元冲突和信元失序.相对于现有方案,PFTSA简化了交换结构和交换流程,同时提高了时延性能.
To solve the time constraint of scheduling algorithm in the feedback-based two-stage switch architecture (FTSA), a new scheme called pulsating feedback-based two-stage switch architecture (PFTSA) is proposed, which transmits the required information back to the input port in a way of pulsating. The accurate data of target buffers can be obtained by the scheduling algorithm with a preprocessing scheme, so as to avoiding the cell conflicting and disordering. As compared to the existing schemes, PFTSA can not only simplify the switch architecture and procedure, but also improve the delay performance.
在网络视频业务、云计算等新型网络业务和新兴技术的驱动下, 终端处的数据传输压力越来越大.密集波分复用技术使单根光纤的数据传输带宽达到10 TB, 这使交换能力相对较弱的中继系统成为当今Internet的数据传输瓶颈.中继设备交换性能关键取决于其交换结构.在这一领域, 业界的研究重点在于输入缓存(IQ, input queued)[1-2]、输入和交叉点缓存(CICQ, combined input-crosspoint-queued)[3-4]、Clos[5-6]及负载均衡交换结构[7-14].其中, 负载均衡交换结构的多级crossbar能够将到达输入端的突发数据流均匀散布, 因此能够较好地适应Internet自相似数据流. Hu和Yeung [9]提出的反馈型两级交换结构(FTSA, feedback-based two-stage switch architecture)巧妙地利用错列对称的crossbar连接方式, 使输入端口能通过反馈提前获得目标缓存数据, 从而实现精准的信元调度, 获得极为优异的时延性能. FTSA是迄今为止理论性能最优的负载均衡交换结构,FTSA的缺陷在于其输入端口的算法必须在crossbar重配置时间内完成调度. crossbar重配置时间本质上取决于交换芯片元器件的开关速度, 当前芯片频率已达到GHz, 即芯片元器件的工作周期为ns级.另一方面, 现有调度算法如最长队列优先(LQF, longest queue first)、最早离开者优先(EDF, earliest departure first)和轮询算法(RR, round-robin)的算法复杂度均为O(N).在ns级时间之内完成复杂度为O(N)的调度算法是不现实的.实践中因调度耗时超出限定的时间区间而不得不延迟信元传输的开始时间,以等待算法调度的结果, 使FTSA优异的理论性能无法实现.
针对这一问题,利用脉动反馈机制为调度算法提供接近一个时隙的执行时间,有效解决了其对调度算法的时间限制问题,提高了实践可行性.
1 相关工作解决FTSA的时间限制问题有两种思路:前置反馈交换结构(FFTS, front-feedback-based two-stage switch architecture)[13]和使用2-错列对称的改进方案(FTSA-2-SS, FTSA using 2-staggered symmetry connection pattern)[14].
FFTS和FTSA-2-SS的交换结构相同, 如图 1所示, 其两级crossbar分别记为X1和X2, 位于X1之前的缓存记为VOQ1, 任意VOQ1(i, k)用于缓存到达输入端口i且目标端口为k的信元;位于X1和X2之间的缓存记为VOQ2,任意VOQ2(j, k)用于缓存到达中间端口j且目标端口为k的信元, 任意VOQ2(j, k)设置2个信元的缓存空间.输出端口设置重排序缓存来纠正信元离开交换机的顺序.
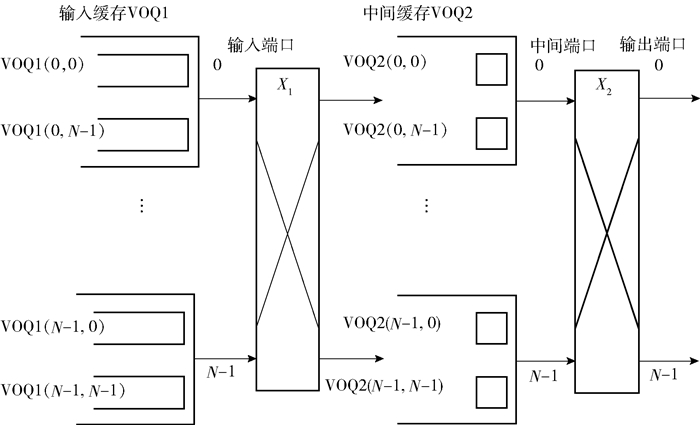
|
图 1 PFTSA交换结构 |
FFTS和FTSA-2-SS均能在一定程度上解决算法执行时间不足的问题, 但付出了巨大的代价.
1) 交换结构复杂化.二者都只能简单地依据不完整的信息进行调度.可能导致“信元冲突”[13-14]问题, 故二者均需为任意VOQ2(j, k)设置“第二信元空间”.第二信元空间虽然可临时缓存发生冲突的信元, 但也丧失了原本的信元保序机制, 故FFTS和FTSA-2-SS均需在输出端设置重排序缓存来纠正信元离开交换机的顺序.
2) 时延性能恶化.信元在第二信元空间和重排序缓存中的等待时间也恶化了时延性能, 仿真实验表明, 在相同的条件下, 二者的时延性能相对于FTSA均有明显的下降.
提出的脉动反馈型两级交换结构(PFTSA, pulsating feedback-based two-stage switch architecture)采用一种前置的脉动反馈机制使得输入端口能够提前获得准确的目标缓存状态数据, 既能扩展算法的执行时间区间, 又能避免信元冲突和信元失序, 无需设置第二信元空间和重排序缓存.
2 脉动反馈型两级交换结构PFTSA采用如图 1所示的交换结构, 其两级crossbar采用错列对称方式[9],其任意VOQ2(j, k)仅设置一个信元的缓存空间.
为便于表述, 做如下约定:
1) 交换结构的输入/输出端口数记为N, 端口号的加减操作实际都要对N取模, 即i-1实质上是(i-1)mod N.
2) 输入端口i记为Ii, 中间端口j记为Mj, 输出端口k记为Ok.
3) Ii与Mj相连记为Ii→Mj, Mj与Ok相连记为Mj→Ok, Ii通过Mj与Ok相连记为Ii→Mj→Ok.
4) Mj在t时隙开始时刻的缓存状态数据记为Qj(tb), Mj在t时隙结束时刻的缓存状态数据记为Qj(te), Qj(tb)和Qj(te)都仅有N bit, 若其第v位为“1”表示VOQ2(j, v)非空, 反之表示VOQ2(j, v)为空.
5) Ii在t时隙之初向中间端口传输N bit的Pi(t), Pi(t)最多只有1 bit为“1”, 其第v位为“1”表示Ii将在t时隙向中间端口传输VOQ1(i, v)中的信元, Pi(t)=0表示Ii在t时隙不向中间端口传输信元.
6) crossbar重配置时间记为TR, 沿X1或X2传送N bit的发送和传播时延之和记为TN;输出端口将N bit的数据反馈至位于同一线卡的输入端口的时间记为TF, 输入端口进行一次预处理的处理时延记为TP;信元在X1或X2上的传输时延和传播时延之和记为TC.因TR、TN、TF、TP等均耗时极短, 故记TSTD=max(TR, TN, TF, TP).
2.1 脉动反馈机制不失一般性, 不妨设t时隙有Ii→Mj→Ok, 则由错列对称连接方式的特性可知:t+1时隙必有Ik→Mj.以t时隙Ik的算法所需信息的传输过程为例,说明脉动反馈机制的工作方法.
1) 0时刻, Ii向Mj传输Pi(t);Mj向Ok传输本地缓存状态数据Qj(tb),如图 2(a)所示.
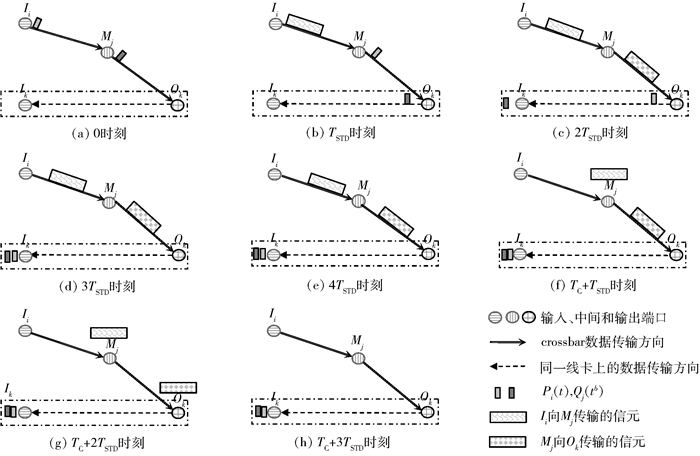
|
图 2 PFTSA的脉动反馈机制 |
2) TSTD时刻, Qj(tb)到达Ok;Pi(t)到达Mj;Ok向Ik反馈Qj(tb);Mj向Ok传输Pi(t);Ii开始向Mj发送信元,如图 2(b)所示.
3) 2TSTD时刻, Qj(tb)到达Ik;Pi(t)到达Ok;Ik对Qj(tb)进行预处理(具体处理方法见2.2节);Ok向Ik传输Pi(t);Mj向Ok发送信元,如图 2(c)所示.
4) 3TSTD时刻, Qj(tb)预处理完成, 结果记为Qj(tbe);Pi(t)到达Ik;Ik开始对Qj(tbe)进行预处理(具体处理方法见2.2节),如图 2(d)所示.
5) 4TSTD时刻, Qj(tbe)预处理完成, 结果即为Qj(te);Ik开始进行调度,如图 2(e)所示.
6) TC+TSTD时刻, 信元到达Mj,如图 2(f)所示.
7) TC+2TSTD时刻, 信元到达Ok,如图 2(g)所示.
8) TC+3TSTD时刻, crossbar重配置完成, 算法调度结束, t+1时隙开始,如图 2(h)所示.
脉动反馈机制的核心在于t时隙之初, Pi(t)依次经Mj和Ok反馈至Ik. Pi(t)是PFTSA能够避免信元冲突和信元失序问题的关键.因为通过Pi(t), PFTSA可得到Mj在t时隙结束时刻其缓存状态的准确数据, 即Qj(te).基于准确的Qj(te)进行“有的放矢”的调度, 不会出现“信元冲突”问题, 自然无需设置第二信元空间, 没有第二信元空间自然不会导致信元失序问题(文献[9]已证明), 因此PFTSA不再需要第二信元空间和重排序缓存.
2.2 信息预处理过程Mj在t时隙开始和结束时刻的缓存状态数据至多只可能有2个bit的不同.
首先考虑t时隙离开Mj的信元, 因t时隙有Mj→Ok, 故若有信元离开, 则必属于VOQ2(j, k).因此预处理方法如下(处理结果记为Qj(tbe)):
| $ {Q_j}\left( {{t^{{\rm{be}}}}} \right) \leftarrow {Q_j}\left( {{t^{\rm{b}}}} \right){\rm{\& }}( \sim (1 \ll (k))) $ |
其次考虑t时隙到达Mj的信元, 因Pi(t)中已经包含了这一信息, 故只需:
| $ {Q_j}\left( {{t^e}} \right) \leftarrow {Q_j}\left( {{t^{{\rm{be}}}}} \right)|{P_i}(t) $ |
处理得到的Qj(te)正是PFTSA中Ik在t时隙的调度算法所需要的准确目标缓存状态数据.
2.3 调度算法PFTSA中调度算法依然采用Hu和Yeung[9]提出的LQF、EDF和RR算法进行调度.
3 相关分析 3.1 算法执行时间的扩展效果基于2.1节分析可知, PFTSA中调度算法的执行时间为TC-TSTD, 运用相同的分析方法, FTSA中调度算法的执行时间不足一个TSTD(TR-TF), FFTS中调度算法的执行时间为TC+TSTD, FTSA-2-SS中调度算法的执行时间为TC+2TSTD.
考虑到TC≫TSTD, 相对于FTSA, PFTSA能够大幅度地改善调度算法的执行时间限制问题.
3.2 交换结构和流程的简化效果相对FFTS和FTSA-2-SS而言, PFTSA无需设置第二信元空间和重排序缓存.
1) PFTSA在每个中间端口节约N个信元空间, 全部N个中间端口共节约N2个信元空间.
2) 申志军等[13]已证明FFTS(FTSA-2-SS类似)需为每个输出端口设置N个信元的重排序缓存, 亦即PFTSA共节约N2个信元空间.
3) 考虑N=32且每时隙转发256 Byte, PFTSA可节约219 Byte的存储空间.
3.3 时延性能因为信元无需在第二信元空间和重排序缓存中等待, PFTSA的时延性能优于FFTS和FTSA-2-SS.但PFTSA的每次调度都是提前进行, 调度开始时尚无法得知本时隙到达本地输入端口的信元信息, 亦即无法转发本时隙到达输入端口的信元, 故相对于FTSA而言, 其时延性能必有所损失.
不失一般性, 以Ik在t时隙的调度算法为例, 当且仅当同时满足下列3个条件时, 对PFTSA的时延性能产生显著负面影响的事件才会发生.
1) t时隙有信元p到达VOQ1(i, v).
2) t时隙p是VOQ1(i, v)中唯一的信元.
3) t时隙p是唯一满足算法需求的信元.
从发生的条件来看, 导致PFTSA时延性能明显损失的概率较低, 故其时延性能损失较为有限.
3.4 代价PFTSA的优势本质上在于以下两方面的折中:
1) PFTSA将调度算法执行时间扩展到TC-TSTD, 大幅度缓解了算法的时间限制问题.
2) 简化了交换流程和结构, 提高了时延性能.
PFTSA的代价在于如下2个方面:
1) PFTSA对调度算法执行时间的扩展效果稍逊于FFTS及FTSA-2-SS.但考虑到TC≫TSTD, 故其对算法执行时间的扩展效果仍然是较为可观的.
2) PFTSA每时隙都会比FTSA多传输N bit, 传输效率会降低.但若以N=32, 每时隙传输256 Byte为例, 效率损失为1.5%, 其代价仍可承受.
4 仿真结果理论上FFTS和FTSA-2-SS在相同的交换环境中具有相同的时延性能,故仅对FTSA、FFTS和PFTSA三种交换结构进行仿真.
基于Opnet14.5,使用32×32的交换模型分别仿真上述3种结构在均匀数据流环境、突发数据流环境和hot-spot数据流环境中的平均时延.
均匀数据流环境预设信元独立且以伯努利分布到达输入端口,信元的目的输出端口服从均匀分布.均匀数据流常用于模拟传统的交换环境.
突发数据流环境预设信元以突发的形式到达输入端口,每个突发块中的信元具有相同的目的输出端口.突发数据流常用于模拟自相似交换环境.
hot-spot数据流环境预设信元独立且以伯努利分布到达输入端口,其中1/3的信元具有相同的目的输出端口,2/3的信元具有相同的另一个目的输出端口. hot-spot数据流常用于模拟不规则的数据流交换环境.
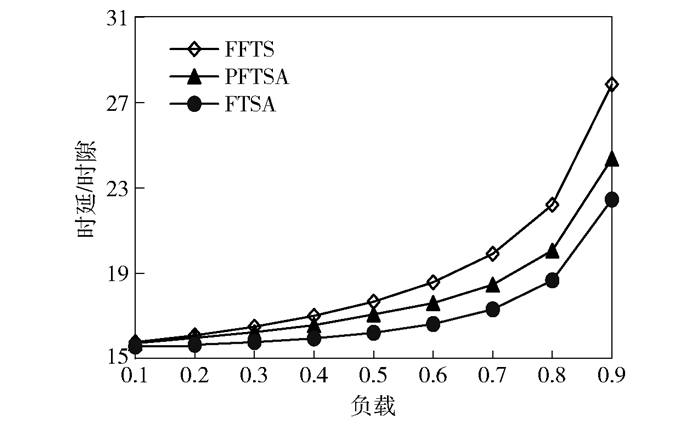
|
图 3 均匀数据流环境中的时延比较 |
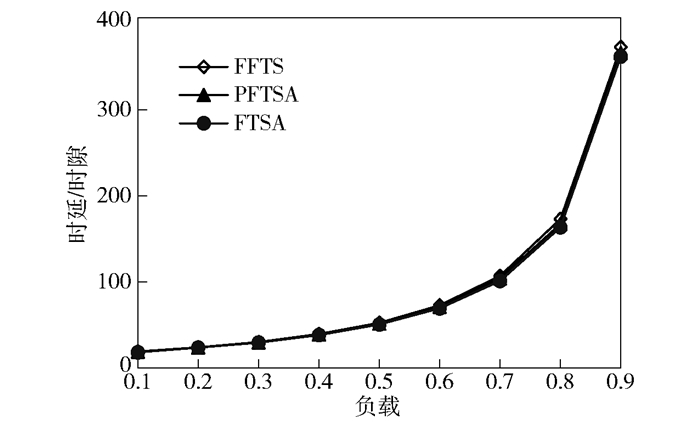
|
图 4 突发数据流环境中的时延比较 |
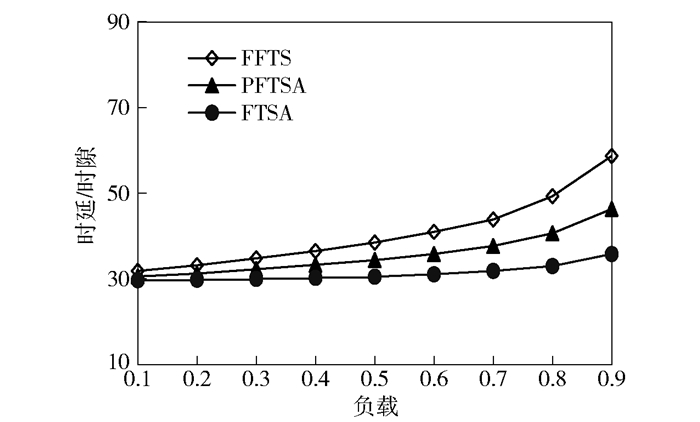
|
图 5 Hot-Spot数据流环境中的时延比较 |
图 3表明,均匀数据流环境下FTSA、FFTS和PFTSA的时延性能均较为优异,其中FTSA的时延性能最好,PFTSA的时延性能优于FFTS,这是因为信元无需第二信元空间和重排序缓存中等待. PFTSA的时延性能略逊于FTSA,原因是其提前调度的策略无法转发当前时隙到达的信元.
图 4表明,在突发数据流环境中,FTSA、FFTS和PFTSA的时延均大幅度上升,但PFTSA的时延性能仍然符合3.3节的性能预期.
图 5表明,3种结构均能较好地适应hot-spot这种不规则的数据流交换环境,PFTSA的平均时延介于FTSA和FFTS之间,依然符合预期.
5 结束语PFTSA通过脉动的形式使得输入端口可提前获得调度算法所必需的准确数据.基于这种机制, PFTSA得以简化交换结构和交换流程, 同时提高了系统的时延性能.下一步研究将从降低算法耗时的角度来进一步缓解反馈型两级交换结构对调度算法的时间限制问题, 使之能够更好地适应未来的高速交换环境.
| [1] |
Xiao Jie, Yeung K L, Jamin S. Pipelined scheduler for unicast and multicast traffic in input-queued switches[C]//2016 IEEE Global Communications Conference. New York: IEEE Press, 2016: 1-6.
|
| [2] |
Hu Bing, Yeung K L, Zhou Qian, et al. On iterative scheduling for input-queued switches with a speedup of 2-1/N[J]. IEEE/ACM Transactions on Networking, 2016, 24(6): 3565-3577. DOI:10.1109/TNET.2016.2541161 |
| [3] |
Jin Hao, Pan Deng, Liu Jason, et al. OpenFlow based flow level bandwidth provisioning for CICQ switches[J]. IEEE Transactions on Computers, 2013, 62(9): 1799-1812. DOI:10.1109/TC.2012.167 |
| [4] |
王斌, 王文鼐. 高性能组合输入交叉点排队交换机[J]. 北京邮电大学学报, 2012, 35(1): 95-98. Wang Bin, Wang Wennai. High performance CICQ fabric[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(1): 95-98. DOI:10.3969/j.issn.1007-5321.2012.01.022 |
| [5] |
高雅, 邱智亮, 张茂森, 等. Clos交换网络中随机化的加权匹配调度算法[J]. 北京邮电大学学报, 2013, 36(4): 90-94. Gao Ya, Qiu Zhiliang, Zhang Maosen, et al. Randomized weight matching dispatching scheme for Clos-network switches[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(4): 90-94. |
| [6] |
Xia Yu, Hamdi M, Chao H J. A practical large capacity three stage buffered Clos network switch architecture[J]. IEEE Transactions on Parallel and Distributed Systems, 2016, 27(2): 317-328. DOI:10.1109/TPDS.2015.2408614 |
| [7] |
Chang C S, Lee D S, Jou Y S. Load balanced Birkhoff-von Neumann switches[C]//2001 IEEE Workshop on High Performance Switching and Routing. New York: IEEE Press, 2001: 276-280.
|
| [8] |
Shen Yanming, Panwar S S, Chao H J. Design and performance analysis of a practical load-balanced switch[J]. IEEE Transactions on Communications, 2009, 57(8): 2420-2429. DOI:10.1109/TCOMM.2009.08.070477 |
| [9] |
Hu Bing, Yeung K L. Feedback-based scheduling for load-balanced two-stage switches[J]. IEEE/ACM Transactions on Networking, 2010, 18(4): 1077-1090. DOI:10.1109/TNET.2009.2037318 |
| [10] |
Cai Yan, Wang Xiaolin, Gong Weibo, et al. A study on the performance of a three-stage load-balancing switch[J]. IEEE/ACM Transactions on Networking, 2014, 22(1): 52-65. DOI:10.1109/TNET.2013.2244906 |
| [11] |
Durkovic S, Cica Z. Birkhoff-von Neumann switch based on greedy scheduling[J]. IEEE Computer Architecture Letters, 2018, 17(1): 13-16. DOI:10.1109/LCA.2017.2707082 |
| [12] |
Huang An, Hu Bing. The optimal joint sequence design in the feedback-based two-stage switch[J]. Journal of Network and Computer Applications, 2014, 45(4): 27-34. |
| [13] |
申志军, 曾华燊, 夏羽. 基于前置反馈的两级交换结构[J]. 通信学报, 2011, 32(5): 56-62. Shen Zhijun, Zeng Huashen, Xia Yu. Front feedback-based two-stage switch architecture[J]. Journal on Communications, 2011, 32(5): 56-62. DOI:10.3969/j.issn.1000-436X.2011.05.008 |
| [14] |
申志军, 曾华燊, 高志江. 一种改进的反馈制两级交换结构FTSA-2-SS[J]. 电子与信息学报, 2011, 33(6): 1319-1325. Shen Zhijun, Zeng Huashen, Gao Zhijiang. An improved feedback-based two-stage switch architecture using 2-staggered symmetry connection pattern[J]. Journal of Electronics & Information Technology, 2011, 33(6): 1319-1325. |


