2. 重庆邮电大学 移动通信技术重点实验室, 重庆 400065
第5代移动通信系统(5G)网络场景下服务功能链的部署是网络功能虚拟化研究中亟待解决的问题,现有部署方法难以在优化时延的同时保证服务功能链部署的可靠性,为此,提出了面向服务质量(QoS)需求的服务功能链部署模型,并设计了一种基于QoS保障的服务功能链动态部署算法.该算法在虚拟网络功能部署阶段通过对网络拓扑和可靠性的感知,采用基于PageRank思想的算法对节点进行评价,以负载均衡和协调链路映射为原则,将虚拟网络功能部署在综合资源能力最大的底层节点上,实现了时延和可靠性的全局优化,并通过选择满足可靠性需求的时延最短路径进行链路映射.仿真结果表明,该算法在降低服务功能链端到端时延的同时保证了部署的可靠性,并且提高了请求接受率和资源利用率.
2. Key Laboratory of Mobile Communication Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
In the fifth generation of mobile communications system (5G), the deployment of service function chaining(SFC) is a critical issue over network function virtualization scenario. A model of SFC deployment forquality of service (QoS) requirements is proposed to solve the problem that the existing methods cannot achieve the optimization of end-to-end delay and reliability of SFC deployment simultaneously. A dynamic deployment algorithm for SFC with QoS guarantee is designed. The method evaluates the nodes based on the approach of PageRank through the perception of network topology and reliability, on the principles of load balancing and coordination with link mapping, the virtual network function(VNF) is mapped onto the substrate node with the highest comprehensive resource capacity which realzes the global optimization of delay and reliability in the VNF mapping phase. The shortest path of delay that meets the reliability requirements is selected for link mapping. The simulation results show that the proposed algorithm can reduce the end-to-end delay and ensure the reliability of SFC, as well as improve the request acceptance rate and resource utilization.
目前,移动网络行业正在迅速向5G演进,移动宽带增强、大规模物联网、低时延高可靠通信三大类新应用领域将发挥重要作用[1]. 5G网络切片是虚拟网络中灵活配置资源的技术,可以快速部署和集中管理[2].在切片网络中,每个业务请求由一些不同的虚拟网络功能(VNF, virtual network function)组成,这些网络功能互联起来称为服务功能链(SFC, service function chaining).每个业务请求的需求不同,会造成每个SFC上的VNF集合不同,如何有效地部署SFC使得在满足切片业务服务质量(QoS, quality of service)的同时最大化虚拟运营商的收益是5G网络中研究的热点问题.
5G移动通信系统低时延场景对通信服务的时延要求较高,需要支持用户毫秒级的端到端网络服务.大多数文献把处理时延和传输时延作为端到端时延进行分析.如Luizelli和Qu[3-4]等把处理时延设为固定值,忽视了节点负载对时延的影响,不符合实际;而Luizelli、Qu和Mijumb[3-5]等没有考虑由网络拓扑以及可靠性造成的时延问题,达不到进一步优化时延的效果.此外,SFC部署过程中,无论是硬件故障还是软件故障,都会破坏整个链路从而导致服务暂停.现有文献多采用基于冗余的VNF部署策略来实现SFC服务的可靠性.如Kanizo等[6]提出了一种规划和部署VNF的备份新方案,应该注意到,这些冗余的VNF将增加SFC的长度,从而增加该服务的端到端时延,降低了资源的利用率.为了减少端到端的时延,可以通过降低VNF冗余的程度实现,以牺牲可靠性为代价.而Qu等[7]提出了一种可重构感知和时延受限服务链(READ)的联合优化框架,该框架保证可靠性的同时权衡了带宽消耗和端到端的时延性能,由于采取了冗余机制,一定程度上增加了端到端时延.
不同于上述文献,为了满足SFC部署的低时延高可靠需求,本文在分析处理时延时考虑节点负载的影响,在此基础上,把链路可靠性作为约束建立模型,并提出了一种基于QoS保障的SFC动态部署算法DDA-QoS.受到Nguyen等[8]提出的节点排序算法的启发,本文采用PageRank思想在VNF部署阶段就考虑到链路的资源容量以及可靠性条件,两阶段协作部署,在不预留资源的情况实现了全局优化时延和可靠性的目标.本文算法有效实现了负载的均衡,最大限度地提高了底层网络的资源利用率,同时保证了端到端的QoS.
1 网络模型与问题描述 1.1 网络场景考虑到5G网络切片的低时延高可靠需求,本文在5G网络场景下研究基于QoS保障的SFC的部署问题.如图 1所示,本文考虑NFV编排和控制架构.图中左方表示系统的编排和管理功能,由管理编排器和SDN控制器组成.其中,管理编排器包括编排器、VNF管理器和基础设施管理器三部分,分别负责图右方SFC业务请求、VNF连接和基础设施全局资源的管理.端到端的SFC业务请求由不同的VNF有序组成,根据它们的资源需求映射到底层网络进行服务.底层网络中,接入网和核心网之间通过SDN网络连接.通过隔离,多个VNF可以在同一个底层节点上运行,互不影响.
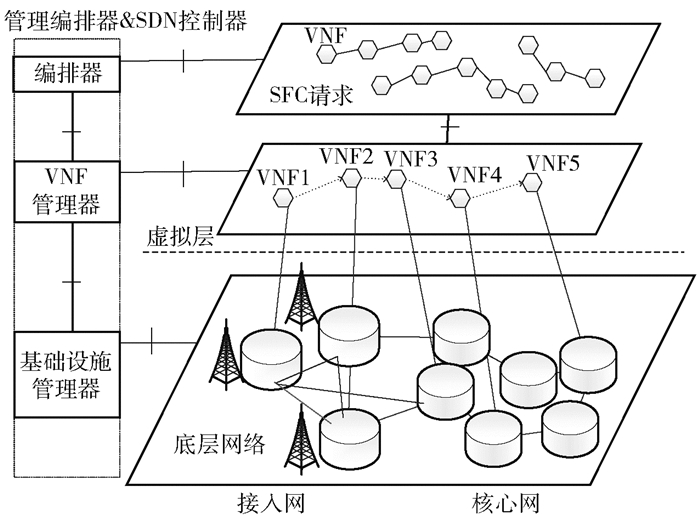
|
图 1 系统场景图 |
本文研究的主要目标就是在该系统场景下,寻找使得SFC部署到底层网络的端到端时延最小的同时能够保障SFC业务请求可靠性的方案.在部署中需要考虑多种因素,如资源容量、节点位置和可靠性等.
1.2 网络模型 1.2.1 底层网络本文把底层网络形式化为一个无向图GS=(NS, LS),NS为底层节点集合,每个节点可以部署一个或多个VNF,LS为所有底层链路的集合.每个底层节点m∈NS的节点CPU容量为CmS,连接节点m和n的链路lmn的带宽为BmnS,可靠性为R(lmn). LmnS是节点m和n之间无环路的路径集合.
1.2.2 SFC请求SFCs链形式化成有向图,表示为GV=(NV, LV),NV为所有的VNF集合,LV为连接VNF的所有虚拟链路的集合.用Q表示单位时间内到达的SFC请求强度,SFC集合表示为S={sq|q=1, 2, …, Q},每个SFC∈Q由VNFs∈NqV⊆NV和连接相邻两个VNF u、v的虚拟链路luv∈LqV⊆LV组成. SFC中每个VNFu的CPU资源需求为CuV,虚拟链路luv带宽需求为BuvV.定义一个二进制变量Amnuv={0, 1}表示虚拟链路luv是否映射到物理链路lmn∈LS上.虚拟链路映射到底层链路后的时延为duv,映射到底层链路后的可靠性不能低于R(luv).
1.3 优化目标要解决的主要问题为:在最大化接入SFC请求数目的前提下最小化端到端时延.同时把5G网络切片业务请求对可靠性需求的差异性作为约束条件.目标函数表示为
| $ \max \left\{ {\sum\limits_{q = 1}^Q q - \sum\limits_{{l_{uv}} \in {L^V}} {{d_{uv}}} } \right\} $ | (1) |
式(1)中第一部分为最大化接入SFC请求的数目,第二部分为最小化端到端时延.约束条件如下:
| $ \left. {\begin{array}{*{20}{l}} {{\rm{Cl}}:\sum\limits_{m \in {N^S}} {x_m^u} = 1, }&{u \in {N^V}}\\ {{\rm{C}}2:\sum\limits_{u \in N_q^V} {x_m^u} \le 1, }&{\forall m \in {N^s}} \end{array}} \right\} $ | (2) |
| $ \left. {\begin{array}{*{20}{l}} {{\rm{C}}3:\sum\limits_{{l_{uv}} \in {L^V}} {\left( {A_{mn}^{uv} + A_{nm}^{uv}} \right)} B_{uv}^V \le B_{mn}^S, \quad \forall {l_{mn}} \in {L^S}}\\ {{\rm{C}}4:\sum\limits_{u \in {N^V}} {x_m^u} C_u^V \le C_m^S, \quad \forall m \in {N^S}} \end{array}} \right\} $ | (3) |
| $ {\rm{C}}5:\sum\limits_{m \in {N^S}} {A_{nm}^{uv}} - \sum\limits_{m \in {N^S}} {A_{mn}^{uv}} = x_n^u - x_n^v, \forall n \in {N^S}, \forall {l_{uv}} \in {L^V} $ | (4) |
| $ {\rm{C}}6:\sum\limits_{{l_{mn}} \in {L^S}} {\left( {A_{mn}^{uv} + A_{nm}^{uv}} \right)} \ge 1, \;\forall {l_{uv}} \in {L^V} $ | (5) |
| $ \prod\limits_{{l_{mn}} \in {L^s}} {\left( {A_{mn}^{uv} + A_{nm}^{uv}} \right)} R\left( {{l_{mn}}} \right) \ge R\left( {{l_{uv}}} \right), \;\forall {l_{uv}} \in {L^V} $ | (6) |
| $ \left. {\begin{array}{*{20}{l}} {{\rm{C8}}:A_{mn}^{uv} = \{ 0, 1\} \;\forall {l_{uv}} \in {L^V}, \;\forall {l_{mn}} \in {L^S}}\\ {{\rm{C}}9:x_m^u = \{ 0, 1\} \;\forall u \in {N^V}, \;\forall m \in {N^S}} \end{array}} \right\} $ | (7) |
C1和C2用于保证SFC请求中的每个VNF只能映射到一个底层节点上,并且一条SFC上的VNF需要部署在不同的底层节点上;C3和C4确保映射到底层节点的SFC的资源需求不能超过底层节点和链路的资源限制;C5和C6表示每条虚拟链路至少映射到一条或多条底层链路上,且必须映射到连续的底层链路上;C7表示必须满足SFC对链路可靠性的最小约束;C8和C9表示节点映射和链路映射的二进制变量约束.
通过SFC中每跳链路的时延叠加来计算端到端时延.每跳链路的时延表示为处理时延dprocuv和传输时延dtranuv的和,即duv=dprocuv+dtranuv.
处理时延与节点需要处理的负载Cmload有关,用式(8)表示,xmu为示VNF u映射到底层节点m上.
| $ C_m^{{\rm{ load }}} = \frac{{\sum\limits_{u \in {N^V}} {x_m^u} C_u^V}}{{C_m^S}} $ | (8) |
当节点的CPU负载增大时,处理时延迅速增加,本文假设处理时延是处理负载的凸函数,使用分段线性化来近似凸时延曲线. αi和βi是用于近似凸时延曲线的线性函数的系数,i∈I是指用于此近似的线性函数的数目.所以,底层节点的处理时延可以表示为
| $ d_{{\rm{proc}}}^m = {\alpha _i} + {\beta _i}C_m^{{\rm{load}}} $ | (9) |
每个物理节点m的处理时延不能超过该节点处理时延最大值dprocm, max .所以每跳链路luv的处理时延表示为
| $ \begin{array}{*{20}{c}} {d_{{\rm{ proc }}}^{uv} = \sum\limits_{m \in {N^S}} {x_m^u} d_{{\rm{ proc }}}^m + \sum\limits_{n \in {N^S}} {x_n^v} d_{{\rm{ proc }}}^n}\\ {\qquad m, n \in {N^S}, m \ne n} \end{array} $ | (10) |
并且满足:
传输时延与需要处理的SFC虚拟链路映射到底层链路的跳数有关,本文假设SFC中每跳链路的传输时延为d′uv,映射到底层链路上的时延可以表示为
| $ d_{{\rm{tran}}}^{uv} = \sum\limits_{{l_{mn}} \in {L^S}} {A_{mn}^{uv}} d_{uv}^\prime $ | (11) |
本文在VNF部署阶段提出了一种基于节点位置和可靠性的节点排序算法,以排序结果作为依据进行VNF的部署.在链路映射阶段提出了一种基于可靠性的链路映射方案.
2.1 节点位置和可靠性本文在对节点重要性进行评价时,引入节点和链路的可靠性以及节点的位置,从而优化SFC的部署.
1) 节点位置.节点位置与节点连接度G(m)、节点的有效性E(m)和适应性T(m)有关.其中,节点的连接度由相邻的链路总数s(m)决定.
| $ \mathit{G}{\rm{(}}\mathit{m}{\rm{) = }}\mathit{s}{\rm{(}}\mathit{m}{\rm{)}} $ | (12) |
节点的有效性用节点效率表示.这里节点效率定义为与其他节点之间的距离的倒数,D(m, n)为节点m和n之间的传输距离.
| $ E(m) = \sum\limits_{n \in {N^S}} {\frac{1}{{D(m, n)}}} $ | (13) |
节点的适应性是指当节点m失效后,所有以最短路径通过m节点相连的其他节点为恢复与m相连的链路所增加通信距离的最小值.
| $ T(m) = \mathop {\min }\limits_{j, h \in {N^S}} D(j, h)j, h \ne m $ | (14) |
2) 节点的可靠性.节点可靠性即节点正常工作概率与节点失效率λm有关.这里节点失效率用平均故障间隔时间(MTBF)和平均修复时间(MTTR)来表示.节点的正常工作概率可以表示为1-λm.
| $ {\lambda _m} = \frac{{{\rm{MTTR}}}}{{{\rm{MTBF}} + {\rm{MTTR}}}} $ | (15) |
3) 链路的可靠性.本文假设链路的失效满足泊松分布,则时间间隔t内,没有发生失效的概率为P=e-λmnt,所以链路的可靠度为R(lmn)=e-λmnt,λmn为链路lmn的失效率,t为链路lmn上的时延.由于本文在进行VNF部署时考虑链路因素,在时延约束下,做出以下转化:
本文采用Google的PageRank算法中的思想,重新定义节点的重要性,表示为
| $ r(m) = (1 - \gamma ){\hat C_m} + \gamma \sum\limits_{n \in J(m)} {\frac{{{{\hat B}_{mn}}}}{{\sum\limits_{x \in J(n)} {{{\hat B}_{xn}}} }}} r(n) $ | (16) |
式中:r(m)为节点m的得分,用于表征节点的重要性;γ为介于0~1之间的阻尼系数;J(m)为与节点m相邻的节点集合;
根据PageRank的思想,本文可以得到最终的节点迭代得分表达式,表示为如下向量形式:
| $ \mathit{\boldsymbol{r}} = (1 - \gamma )\mathit{\boldsymbol{C}} + \gamma \mathit{\boldsymbol{Hr}} $ | (17) |
式中:r=(r(1), r(2), …, r(|NS|))T;C=(C(1), C(2), …, C(|NS|))T;H为维度为|NS|×|NS|的转换矩阵,每个元素为
| $ \mathit{h}{\rm{(}}\mathit{m}{\rm{, }}\mathit{n}{\rm{) = }}\left\{ \begin{array}{l} \frac{{{{\hat B}_{mn}}}}{{\sum\limits_{x \in J(n)} {{{\hat B}_{xn}}} }}\quad (m, n) \in l\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (18) |
通过化简,本文可以得到
| $ \mathit{\boldsymbol{r}} = (1 - \gamma ){(\mathit{\boldsymbol{I}} - \gamma \mathit{\boldsymbol{H}})^{ - 1}}\mathit{\boldsymbol{C}} $ | (19) |
因为要得到式(19),I-γH矩阵必须是可逆的,所以做出以下证明.由于:
| $ \sum\limits_{m \in {N^S}} h (m, n) = \sum\limits_{m \in J(n)} {\frac{{{{\hat B}_{mn}}}}{{\sum\limits_{x \in J(n)} {{{\hat B}_{xn}}} }}} = 1 $ | (20) |
根据矩阵相关理论,得出结论‖H‖≤1.为了证明矩阵I-γH是可逆的,这里采用反证法.如果矩阵I-γH是不可逆的,则(I-γH)x=0肯定有非零解,即x是一个非零向量,从而得到γHx=x,通过转化为向量求解的范数形式,得到:‖x‖=‖γHx‖≤γ‖H‖‖x‖,因为x是一个非零向量,所以可以进一步得出‖H‖≥
基于节点位置和可靠性的节点排序算法步骤如算法1所示.该算法通过不断地迭代,最终得到得分的平稳分布,以此为依据进行VNF的部署.根据文献[9],算法1的时间复杂度为O(|NS|2
算法1 基于节点位置和可靠性的节点排序算法
1 初始化网络拓扑G=(NS, LS), 预先设定一个小的正值σ;
2 计算矩阵H和初始向量C;
3 定义迭代次数k,初始化k=0;
4 定义变量w,初始化w=∞;
5 当w≥σ时,计算r=(1-γ)(I-γH)-1C,计算w=abs(rk+1-rk),令k=k+1,直到w≥σ条件不满足;
6 输出最后结果r.
2.2.2 基于节点排序的VNF部署算法在节点排序算法的基础上进行VNF的部署,具体步骤如算法2所示.第2步执行算法1进行虚拟节点归一化中的资源状态表示为
算法2 基于节点排序的VNF部署算法
1 执行算法1,计算出底层节点的重要程度r(m),然后进行排序,sort(m′, descend′);
2 对SFC按照算法1,计算VNF的重要程度r(u),进行排序,sort(u′, descend′);
3 for SFC中排序过的每个VNF u
for底层网络排序过还未被该SFC中VNF部署的节点m
if CmS>CuV
把该VNF u映射到该底层节点m上,
break;
end
end
end
4 如果步骤3中该SFC的VNF全部成功部署到底层节点,开始进行链路映射,否则拒绝该SFC.
2.3 基于可靠性的链路映射方案在VNF部署成功后,需要进行链路的映射,具体算法步骤如算法3所示.首先根据SFC中每条子链路的可靠性要求进行大小排序,选择可靠性要求较高的链路进行映射,删除所有不满足该SFC相应子链路需求的底层链路,减少搜索空间,提高映射效率.然后执行K-最短路径算法选出K条时延最短的路径,按照时延大小递增排序.最后选择满足该SFC的链路可靠性约束的时延最短路径.这样能够在保证SFC请求映射可靠性的前提下使得时延最小化.链路映射算法的时间复杂度为O(K|LV||LS|log |NS|).
算法3 基于可靠性的链路映射算法
1 对已经完成VNF部署的SFC q的每跳链路按照可靠性需求排序,可靠性要求高的排在前面;
2 for luv∈sq do
3 for lmn∈LS do
if BmnS<BuvV
cut lmn∈LS
end
end
4 执行K最短路径算法找出K条时延最短路径,当k=1时,时延最短,k=K时时延最大;
5 for k=1 to K
if exp
break;
end
end
6 如果步骤5中没有满足可靠性约束的路径,则拒绝该SFC;
7 end
通过上述分析,本文基于QoS保障的SFC动态部署算法总的时间复杂度为
为了评价本文算法的有效性,定义了以下评价标准:接受率、端到端时延、链路利用率、节点CPU利用率以及节点和链路的可靠性.并与基于贪婪的最小负载SFC部署算法(GLL)[5]和基于全局资源排序的SFC部署算法(SFC-GRC)[10]进行了比较.
3.1 仿真设置使用基于GT-ITM工具生成随机的底层网络图和SFC请求.每对底层节点之间等概率生成物理链路.物理节点CPU资源和链路带宽均匀地分布在[50, 100]单元之间.每个物理节点均匀分布在以x和y为坐标轴的[0, 100]之间的随机区域内.假设SFC请求动态到达,且服从单位时间内到达强度为[1, 30]的泊松分布.每个SFC请求由一个或多个VNF组成,数量服从[2, 5]的均匀分布. SFC中的VNF CPU和链路的容量需求均匀地分布在[30, 35]单元之间.式(16)中的γ值设置为0.8.对每次仿真结果重复50次求平均值以提高仿真的准确性.
3.2 性能分析从图 2中可以看出,随着请求强度的增加,算法的接受率逐渐降低.本文算法的降低幅度相对GLL和SFC-GRC两种算法较低.这是因为GLL算法只考虑了底层节点CPU资源的使用情况,没有考虑链路容量以及节点位置的影响.而SFC-GRC算法没有考虑节点位置的影响.本文算法充分考虑了节点和链路的影响因素,使得SFC请求能够相对均匀地部署在底层网络中,实现负载的均衡,可以接受更多的SFC请求.
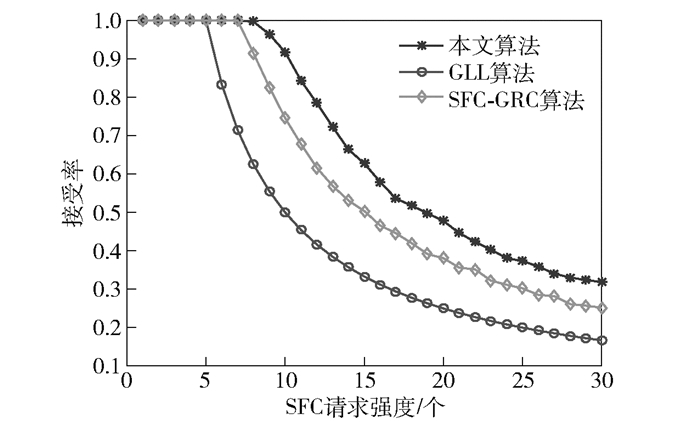
|
图 2 SFC请求接受率对比 |
从图 3可以看出,本文算法明显优于其他两种算法.这是因为本文算法不仅考虑了节点和链路容量的限制,同时考虑了网络拓扑的影响,实现了节点负载的均衡使得处理时延降低,也使得数据流通过底层链路的传输时延降低.而GLL算法只考虑了节点容量的影响,没有考虑底层链路的影响,导致传输时延过长. SFC-GRC算法没有考虑节点位置的影响,也会导致传输时延过长.
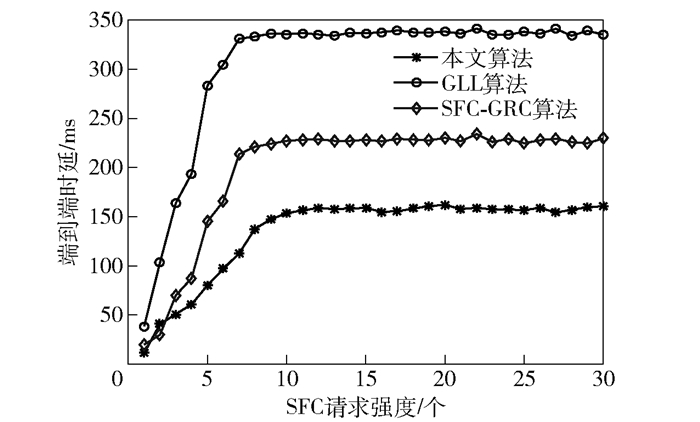
|
图 3 端到端时延对比 |
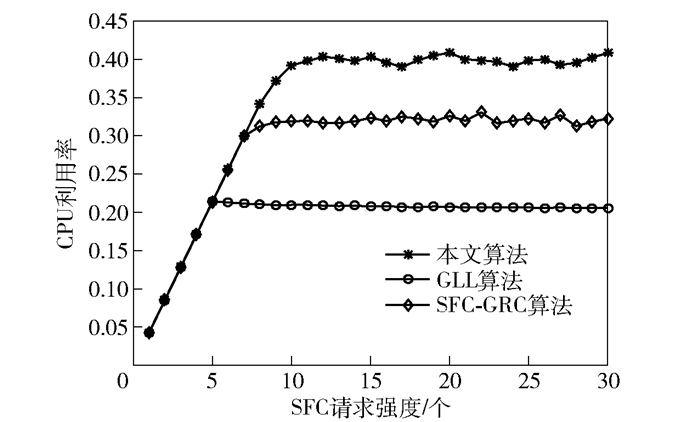
从图 4和图 5可以看出,本文算法相对于其他两种算法节点CPU利用率高,链路利用率少.这是因为本文算法实现了负载的均衡使得接受率较高,所以节点CPU利用率高,与此同时,本文算法消耗较少的链路资源实现较高的接受率,充分提高了资源的利用率.
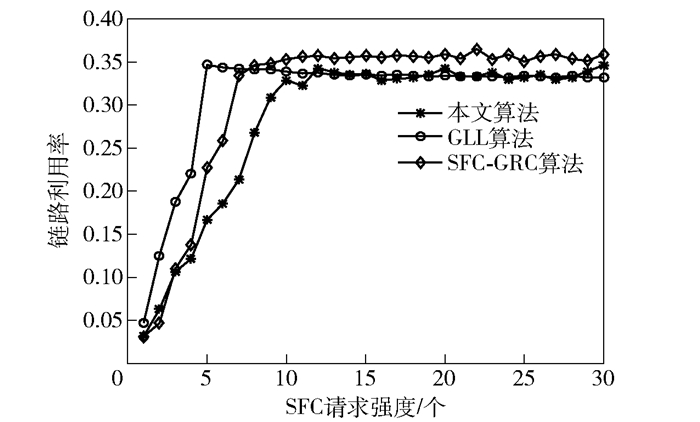
|
图 4 链路利用率对比图 |
|
图 5 节点CPU利用率对比 |
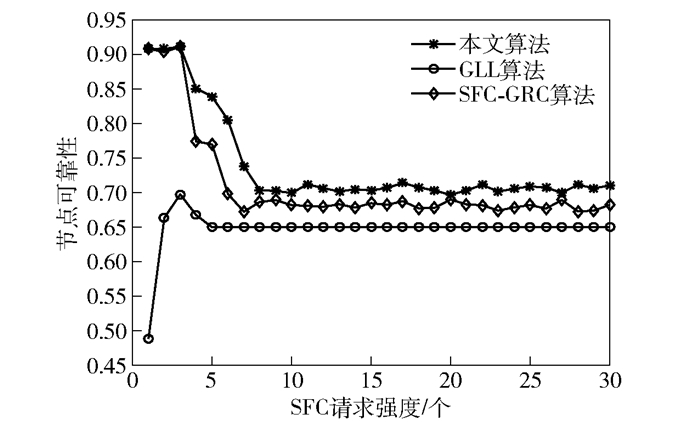
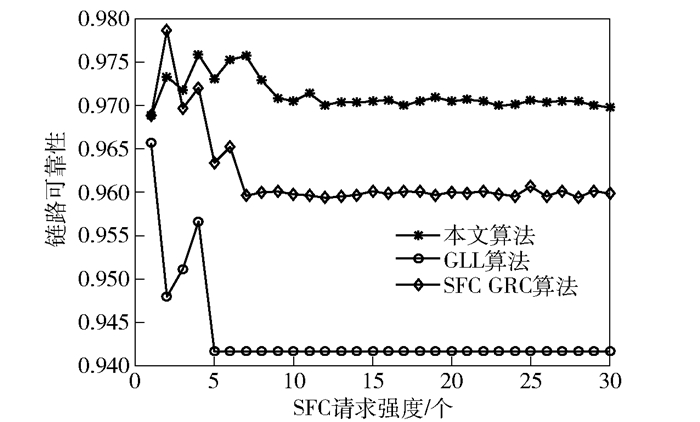
从图 6和图 7可以看出,由于本文算法考虑了节点可靠性和链路可靠性对SFC部署的影响,优先选择可靠性比较高的节点和链路进行SFC的部署,所以本文算法的可靠性明显优于其他两种算法.
|
图 6 节点可靠性对比图 |
|
图 7 链路可靠性对比 |
本文提出了基于QoS保障的服务功能链动态部署算法DDA-QoS.针对5G网络低时延高可靠场景的需求和传统SFC部署方法的不足,本文在研究时延问题的同时把节点和链路的可靠性考虑进来,保证了SFC部署的可靠性,并验证了算法的可行性和有效性.
本文算法根据节点位置和可靠性选择节点进行SFC的部署,实现负载的均衡降低处理时延,同时寻找满足可靠性约束的时延最短路径减少传输时延,体现了全局优化时延和可靠性的性能.仿真结果表明,本文算法在SFC请求接受率、端到端时延、节点和链路利用率以及节点和链路可靠性性能方面有显著的提升.由于5G C-RAN架构的提出,协议层的划分不同,可能会有不同的性能,VNF在接入网的有效部署方案需要提出.所以在后续研究中,将针对接入网中VNF部署进行研究.
| [1] |
Mahmood N H, Lauridsen M, Berardinelli G, et al. Radio resource management techniques for eMBB and mMTC services in 5G dense small cell scenarios[C]//84th IEEE Vehicular Technology Conference. New York: IEEE Press, 2016: 1-5.
|
| [2] |
Rahman M M, Despins C, Affes S. Design optimization of wireless access virtualization based on cost and QoS trade-off utility maximization[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6146-6162. DOI:10.1109/TWC.2016.2580505 |
| [3] |
Luizelli M C, Bays L R, Buriol L S, et al. Piecing together the NFV provisioning puzzle: Efficient placement and chaining of virtual network functions[C]//IFIP/IEEE International Symposium on Integrated Network Management. New York: IEEE Press, 2015: 98-106.
|
| [4] |
Qu Long, Assi C, Shaban K. Delay-aware scheduling and resource optimization with network function virtualization[J]. IEEE Transactions on Communications, 2016, 64(9): 3746-3758. DOI:10.1109/TCOMM.2016.2580150 |
| [5] |
Mijumbi R, Serrat J, Gorricho J L, et al. Design and evaluation of algorithms for mapping and scheduling of virtual network functions[C]//1st IEEE Conference on Network Softwarization. New York: IEEE Press, 2015: 1-9.
|
| [6] |
Kanizo Y, Rottenstreich O, Segall I, et al. Optimizing virtual backup allocation for middleboxes[C]//24th IEEE International Conference on Network Protocols. New York: IEEE Press, 2016: 1-10.
|
| [7] |
Qu Long, Assi C, Shaban K, et al. A reliability-aware network service chain provisioning with delay guarantees in NFV-enabled enterprise datacenter networks[J]. IEEE Transactions on Network and Service Management, 2017, 14(3): 554-568. DOI:10.1109/TNSM.2017.2723090 |
| [8] |
Nguyen T M, Fdida S, Pham T M. A comprehensive resource management and placement for network function virtualization[C]//3rd IEEE Conference on Network Softwarization. New York: IEEE Press, 2017: 1-9.
|
| [9] |
Bianchini M, Gori M, Scarselli F. Inside PageRank[J]. ACM Transactions on Internet Technology, 2005, 5(1): 92-128. DOI:10.1145/1052934 |
| [10] |
Gong Long, Wen Yonggang, Zhu Zuqing, et al. Toward profit-seeking virtual network embedding algorithm via global resource capacity[C]//33rd IEEE Annual Conference on Computer Communications. New York: IEEE Press, 2014: 1-9.
|


