2. 北京工业大学 北京未来网络科技高精尖创新中心, 北京 100124
针对域名系统(DNS)中存在异常查询的问题,提出了一种基于日志信息的DNS查询异常检测算法,以检测异常的互联网协议地址(IP).通过分析DNS正常与异常请求行为的区别,提取了DNS日志中多个维度的信息来表征源IP;其次,利用降维处理将数据映射到三维空间,以便直观地可视化呈现和快速地进行数据分析;最后,利用聚类分析和计算各源IP的可信度,检测出异常的源IP.实验结果表明,所提算法不但能直观观察到多维数据集中的关联特性,而且能从全局和局部2个层面识别网络中异常的源IP.
2. Beijing Advanced Innovation Center for Future Internet Technology, Beijing University of Technology, Beijing 100124, China
Point at the anomaly queries existing in domain name system (DNS), an anomaly detection algorithm based on DNS query logs is proposed to detect suspicious and abnormal internet protocol addresses (IP). First, multiple dimensions of information in the DNS logs are extracted to characterize the source IPs after analyzing the difference between normal DNS query behaviors and the abnormal ones. Secondly, the datasets are mapped to a three-dimensional space through dimensionality reduction, which is beneficial for intuitive visualization and rapid data analysis. Finally, clustering the source IPs and calculating the credibility of them to identify the abnormal ones. The experiment results show that this algorithm can not only observe the correlation characteristics of multi-dimensional datasets directly, but also identify the abnormal source IPs in the global and local aspects.
随着互联网特别是移动网络领域的迅猛发展,网络环境及用户群体日趋复杂,由此带来的网络安全问题也日益严峻.作为互联网中最核心的基础设施之一,域名系统(DNS,domain name system)[1]是大多数网络应用与服务的基础,其实现域名与IP的快速映射与转换,在本质上是规模庞大的分布式数据库系统.
然而,现有的DNS协议未能提供信息保护和认证机制,同时DNS安全扩展(DNSSEC,domain name system security extensions)存在系统效率低下及统一部署困难等问题,这种现状给DNS的安全带来了极大的隐患.因此,一些恶意攻击者利用DNS尚未完善的机制进行攻击,如针对DNS的DDOS(distributed denial of service)攻击,通过受害主机向DNS服务器发送大量伪造的DNS查询请求,导致DNS服务器的缓存资源被耗尽或忙于发送回应包而造成拒绝服务.
目前,在基于DNS查询的网络攻击的检测方面,Shan等提出了利用热力图与树形图结合分析区域和时间特征,以实现DNS的异常检测[2]; 林成虎等提出了一种基于权重的K-means聚类与多特征检测的DNS查询异常检测算法[3];王靖云等提出了基于相对密度的DNS请求异常检测算法[4];马云龙等提出了基于连接数、流量和数据分组等流量特征来实现DNS查询异常检测[5];周昌令等提出了利用自然语言处理与深度向量嵌入的DNS查询异常检测算法[6].然而,大部分这类研究工作都是从DNS流量攻击的角度根据某些异常特征而进行直接检测,缺少对源IP行为特征的深度分析;此外,这些检测算法往往实时性较差,面对多变与未知的DNS查询攻击行为,难以行之有效的适应与应用.针对这种情况,本文提出了一种利用低维可视化与数据点可信度相结合的分析算法.
本文的主要贡献如下.
1) 提出了一种针对源IP的可视化方法,通过提取DNS查询日志信息将源IP表征为多维数据点,再利用核主成分分析(KPCA,kernel principal component analysis)算法[7]将源IP映射到低维特征空间中.通过降维处理,不但避免了因多维空间中数据分布稀疏、重叠度高、距离计算困难从而导致直接计算时间长、分析误差大等问题,而且能最大限度地保留有效信息以及直观地观察到源IP间的关联特性.
2) 提出了一种在低维空间中对异常源IP的检测算法,对低维空间中数据点进行K-means分析, 计算同簇内各点的可信度,将可信度低的作为异常源IP,以各簇的质心点的特征作为其簇的总体特征,对各簇的总体特征分析以标记出异常簇.同时,采用Davies-Bouldin(DB)[8]指标以分析数据点的低维分布特点,并依此寻找出最佳的簇数.
3) 使用真实的主干网的DNS服务器的查询日志作为数据源.经过实验分析,能直观观察到源IP间隐含关联,结合可信度指标及各簇质心点的特征,能精确与快速地检测出异常的源IP.
1 基于DNS查询的异常检测算法本文提出的源IP异常检测算法使用的数据源是DNS服务器的查询日志.首先,通过特征提取与降维处理实现高效提取主要信息.其次,基于DB指标的K-means算法分析低维特征空间中数据分布特点.最后,对异常源IP查找过程可分为两部分:其一,对聚类后各簇的源IP计算其周围密度作为可信度指标,各簇的可信度最低的几个源IP视为异常;其二,将各簇的质心点的特征属性作为该簇的总体特征,通过分析各簇的总体特征可判断出该簇是否为异常簇.综上,本文针对DNS查询的异常源IP检测算法的基本流程如图 1所示.

|
图 1 基于日志信息的DNS查询异常检测算法流程 |
为了实现最大程度地表征DNS查询行为,在分析了DNS查询行为与DNS日志记录属性关联的基础上,本文构建了数据统计特征向量来描述源IP.其中,特征向量的8个属性如下.
1) DNS查询总次数.正常源IP的DNS查询请求一般不会太多,当出现DDOS攻击、僵尸网络时,异常IP的DNS查询次数会急速飙升.
2) DNS查询次数峰值.源IP的单位时间内DNS请求总次数不多,但DNS请求次数峰值过高,该IP也可能存在异常.
3) 源端口的信息熵.为了避免被劫持,一般DNS请求的端口号往往是随机的.引入信息熵则很好地衡量源IP端口号的随机性,端口随机性越高,其信息熵越大.
4) 报文头部ID的信息熵.与源端口类似,报文头部ID通常也是随机产生的,较低的报文头部ID信息熵表明源IP可能存在异常.
5) 域名种类的信息熵.域名种类是指权威域的种类.单位时间内的DNS请求的域名种类的信息熵反映出源IP的行为特征.
6) 非法域名的比例.正常源IP的DNS请求所产生的非法域名的比例通常较低,异常源IP则会有较高的非法域名的比例.
7) 错误报文的比例.与非法域名类似,正常源IP几乎不存在错误的DNS报文.
8) 服务器处理失败的比例.通常,服务器处理失败往往是因为服务器自身的原因、不支持查询类型、因设置的策略拒绝给出应答等.
对于特征的实际最小值和最大值未知的情况,如单位时间内的DNS请求次数、DNS请求次数的峰值进行标准分数标准化处理,具体公式如下:
| $ X_{i, j}^\prime = \frac{{{X_{i, j}} - {\mu _j}}}{{{\delta _j}}} $ | (1) |
其中:Xi, j(i=1, 2, …, n;j=1, 2, …, m)为提取特征后的样本数据, n为数据个数,m为数据的特征属性维度;μj为Xi, j在特征维度j下的均值;δj为Xi, j在特征维度j下的标准差.
1.2 核化主元分析实际上,在高维情形中存在样本分布稀疏、距离计算困难等现象,是所有机器学习算法都面对的重大挑战,被称为“维数灾难”.缓解维数灾难的主要途径就是降维,也称为“维数约简”,即利用某种数学变换将高维数据空间映射为低维特征空间,在低特征空间中样本密度大幅提高,计算距离亦将简化.降维处理,直观上便于数据的计算和可视化,更深层次的意义在于有效信息的提取及信息损失最小化.
以高维空间到低维空间的函数映射是否线性作为划分标准,降维算法分为线性降维和非线性降维两种.线性降维算法主要有主成分分析(PCA,principal component analysis)和线性判别式分析(LDA,linear discriminant analysis). PCA在降低数据集维度的同时,保留对数据集贡献最大的特征.非线性降维算法主要有基于重建权值的局部线性嵌入(LLE,locally linear embedding)算法、基于核的KPCA与核熵成分分析(KECA,kernel entropy component analysis)[9]等.
本文采用KPCA算法对特征提取后的数据集降维处理,为了低维空间下数据可视化的需要,一般把多维数据映射到二维或三维空间.
KPCA的基本思想是将输入的多维数据集通过隐式映射到一个高维Mercer特征空间,在高维Mercer特征空间中再进行主成分分析.假定中心化后数据的协方差矩阵Z为
| $ \mathit{\boldsymbol{Z}} = \sum\limits_{i = 1}^n \mathit{\Phi } \left( {{\mathit{\boldsymbol{x}}_i}} \right)\mathit{\Phi }{\left( {{\mathit{\boldsymbol{x}}_i}} \right)^{\rm{T}}} $ | (2) |
其中:xi为原始属性空间中的样本点,Φ(xi)为xi映射到高维特征空间的像.
设Z的特征值为λ,对应的特征向量为ω,则有
| $ \mathit{\boldsymbol{Z\omega }} = \lambda \mathit{\boldsymbol{\omega }} $ | (3) |
其中
将Φ(xk)(k=1, 2, …, n)与式(3)作内积,则有
| $ \begin{array}{l} \lambda \sum\limits_{i = 1}^n {{a_i}} \left( {\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_i}} \right)\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right) = \\ \frac{1}{n}\sum\limits_{i = 1}^n {{a_i}} \sum\limits_{j = 1}^n {\left( {\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_j}} \right)\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right)} \left( {\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_j}} \right)\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_i}} \right)} \right) \end{array} $ | (4) |
定义核矩阵K为
| $ \mathit{\boldsymbol{K}} = {\left( {k\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right)} \right)_{n \times n}} $ | (5) |
其中
| $ k\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right) = \mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_i}} \right)\mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_j}} \right) $ | (6) |
一般,一个对称函数所对应的矩阵半正定,其就能作为核函数使用.常用的核函数有线性核、多项式核、高斯核、拉普拉斯核等.其中,多项式核与高斯核表达式如式(7)和式(8)所示.
| $ k\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right) = {\left( {\mathit{\boldsymbol{x}}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_j}} \right)^d} $ | (7) |
| $ k\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right) = \exp \left( { - \frac{{{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|}^2}}}{{2{\delta ^2}}}} \right) $ | (8) |
其中δ>0为高斯核的带宽.
将式(5)化简得
| $ \mathit{\boldsymbol{Ka}} = \lambda \mathit{\boldsymbol{a}} $ | (9) |
显然,式(9)是特征值分解问题,取核矩阵K中最大的几个特征值对应的特征向量即可构成映射矩阵.将多维数据投影到选取的特征向量上,即可得到低维空间中的投影.
1.3 K-means聚类通常,降维后的坐标轴并无明确的实际意义,但低维特征空间的数据集分布情况却能表征出原高维数据集中样本的关联特性.因此,对降维后数据集样本的结构进行分析就具有重要意义.这里,采用K-means算法对低维数据集进行聚类分析,以便于对降维的效果进行评估,同时为后续对各样本点可信度的计算作准备.
K-means算法针对聚类所得簇划分最小化平方误差,被广泛应用于各种聚类分析中.相较于其他聚类算法,K-means算法是较为高效的算法,同时较易于应用到如Spark、Hadoop这样的大数据处理平台.
然而,K-means算法却存在k值难以估计的问题,如何恰当地选择k值将直接影响到数据分析与异常检测的结果,故采用基于数据集样本几何结构的DB指标作为确定k值的依据. DB指标描述样本的类内散度与各聚类中心的间距,定义为
| $ {\mathop{\rm DB}\nolimits} (k) = \frac{1}{k}\sum\limits_{i = 1}^k {\mathop {\max }\limits_{_{j = 1 \sim k, j \ne i}} } \left( {\frac{{{W_i} + {W_j}}}{{{C_{ij}}}}} \right) $ | (10) |
其中:k为聚类数目;Wi为簇中的所有样本到其聚类中心Ci的平均距离;Cij为类Ci和Cj中心之间的距离.
由分析可知,DB越小,表示类与类之间的相似度越低,从而对应较佳的聚类结果.
1.4 异常数据点检测低维特征空间中,异常源IP的检测可分为两部分:一部分是对簇内异常数据点的检测;另一部分是对异常簇的检测.
对簇内异常数据点的检测主要是:计算低维特征空间中源IP的周围密度,并将其作为可信度指标.因此,周围密度较低的点其可信度较低,周围密度较高的点其可信度较高.
设点a与点b是簇Ci中的2个点,点a与点b间的距离定义为欧氏距离,即
| $ {\mathop{\rm dis}\nolimits} (a, b) = \sqrt {\sum\limits_{i = 1}^m {{{\left( {x_i^{(a)} - x_i^{(b)}} \right)}^2}} } $ | (11) |
定义a的周围密度为计算点a与其最近的n个点的平均距离的倒数,即
| $ {\mathop{\rm den}\nolimits} (a, n) = {\left( {\frac{{\sum\limits_{b \in N(a, n)} {{\mathop{\rm dis}\nolimits} } (a, b)}}{n}} \right)^{ - 1}} $ | (12) |
通过对可信度的计算,将各簇中可信度较低的几个点作为疑似异常源IP.最终,异常源IP的判定根据较长时间内疑似异常源IP出现频率,即若异常源IP在多个时间段内多次出现则最终判定为异常,反之则判定为正常.
对异常簇的检测主要是:利用k个簇的质心点来代表各簇的DNS查询行为的总体特征.由于大规模DNS查询攻击的存在,如DDOS、僵尸网络入侵等,往往会存在某一簇数据点全部是异常的情况.利用低维可视化呈现及结合质心点的高维行为特征进行分析,能有效地识别各种多变的大型网络入侵行为.
2 实验方法和数据分析本文采用MATLAB平台作为实验平台,其中采用MATLAB Toolbox for Dimensionality Reduction工具箱来实现降维算法.实验对几种不同降维算法的结果进行了对比分析,以验证基于高斯核的主成分分析(GKPCA,Gaussian kernel principal component analysis)在算法复杂度、数据低维分布上拥有较优异的性能.
本文实验的数据来源是某骨干网的DNS服务器的日志信息. DNS日志数据的格式如下:1510303258xxx|183.207.xxx.xxx|18560|111.13.xxx.xxx|34903|www.baidu.com|A||0|.其中,1510303258xxx表示DNS查询的时间戳,183.207.xxx.xxx表示DNS查询的源IP,18560表示DNS查询的端口号,34903表示DNS报文的头部ID,www.baidu.com表示DNS查询的域名,A表示DNS查询类型,0表示DNS查询的应答码.
对DNS查询日志信息提取的过程,考虑到异常检测的实时性,设定提取时长为30 s,故源IP的DNS查询总次数为时长为30 s的DNS查询次数;设定DNS查询次数峰值为源IP选定时段内每5 ms的最大查询次数;域名种类的信息熵指计算该时段内权威域种类的熵值,如www.baidu.com,其权威域为baidu.com;非法域名、错误报文、服务器处理失败的比例是依据应答码以判定源IP每次DNS查询的异常情况,若无异常则应答码为0.对提取完特征的样本数据,分别对DNS查询总次数与DNS查询次数峰值标准化处理.最终,对选定30 s的共740 375条DNS查询日志记录进行处理,得到3 463条源IP的多维数据集.
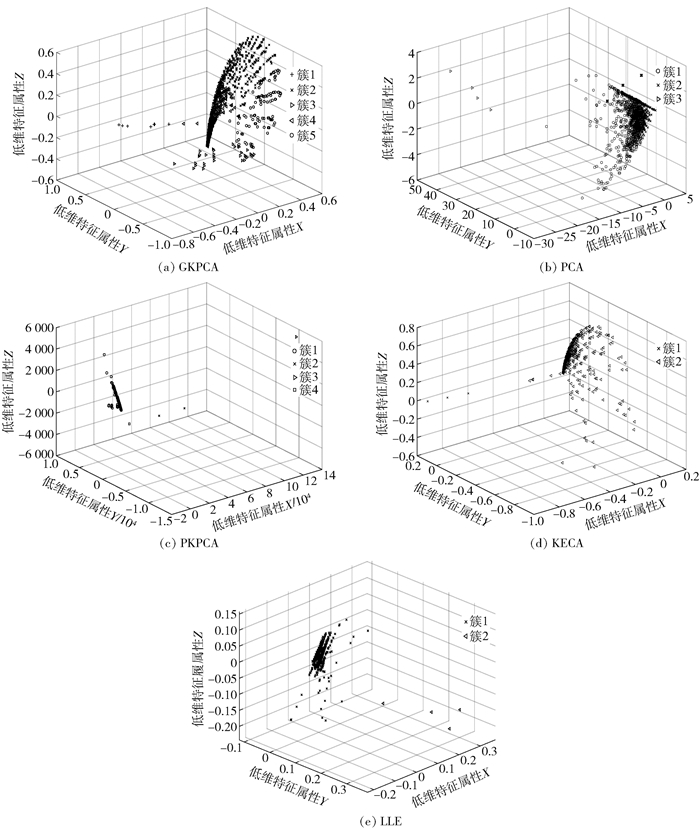
对多维数据集降维处理的过程中,实验将PCA算法、GKPCA算法、基于多项式核的主成分分析(PKPCA,polynomial kernel principal component analysis)算法、KECA算法与LLE算法的结果进行比较.同时,对不同降维算法得到的低维数据集以DB指标确定其最佳聚类结构,再进行K-means处理.各降维算法处理后的低维数据分布情况如图 2所示.
|
图 2 不同降维算法处理后的低维数据分布 |
表 1展示了不同降维算法处理后低维数据的分布情况,其中最佳k值为以DB指标为依据确定的最佳簇数,算法运行时间不包含对日志信息的提取时间.
|
|
表 1 不同降维算法的运行情况 |
通过利用聚类后三维特征空间的分布情况与算法运行时间来判断降维算法效果,其中三维特征空间维度的绝对值并无实际意义.一般认为,最佳簇数越高、簇内数据点数越多、数据分布重叠度越低,则代表着有效信息的提取越充分及信息损失越小,表明降维算法处理结果越优异.
首先,对PCA、PKPCA、GKPCA的降维结果进行比较.由图 2和表 1可知,聚类后三维特征空间中PCA、PKPCA与GKPCA的最佳聚类簇数相似,但相较于GKPCA算法,PCA与PKPCA存在低维空间下数据分布重叠度高且存在部分簇的数据点较少的情况,不利于离群数据点的检测以及观察到各源IP的隐含关联特性.故虽然GKPCA算法的运行时间相对较长,但其有效信息提取更充分,在后续的聚类处理与可信度计算中表现更优异.
然后,对GKPCA、KECA、LLE的降维结果进行比较.这里的KECA算法同样采用高斯核作为核函数,KECA是以其核矩阵特征值与特征向量的Renyi熵来确定映射矩阵,而GKPCA按照其核矩阵特征值的大小来确定映射矩阵, 故GKPCA的算法复杂度要低于KECA.综合考虑最佳簇数、簇内数据点数、数据分布重叠度与运行时间,可以发现GKPCA降维效果更出色.
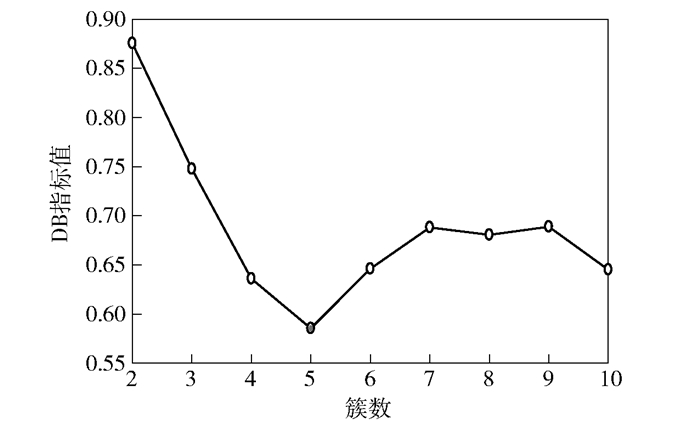
综上所述,采用KPCA作为降维算法,特别是采用GKPCA算法在实际检测中拥有更为优异的表现,其中降维后进行K-means分析的DB指标分布如图 3所示.由图 3可知,GKPCA降维后的数据进行K-means处理的最佳簇数为5.
|
图 3 三维特征空间中数据的DB指标 |
对聚类后各簇数据点分别计算其可信度,设定可信度较低的前1%的源IP作为疑似异常点.最终,截取的部分簇内疑似异常IP如下:序号33的源IP的总访问次数为6,非法域名比例为100%,域名种类熵值为0;序号2996的源IP的总访问次数为8,非法域名比例为100%,域名种类熵值为0;序号1475的源IP的总访问次数为2,服务器处理失败比例为100%等.
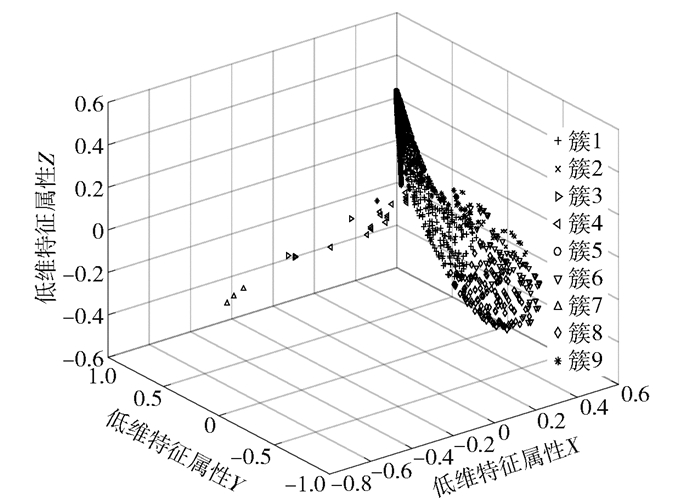
经过对源数据各簇质心点所对应的源IP的多维数据进行分析,并未发现有异常簇.故加入100个源IP作为攻击节点来模拟大规模网络攻击情况,设定其具有较高的DNS查询总次数、DNS查询次数峰值以及非法域名比例,处理后源IP特征三维分布图如图 4所示.
|
图 4 降维处理后模拟攻击的数据分布 |
增加数据点后,因KPCA是保留全局特征的降维算法,故并非简单地在原低维空间中增加数据点,而是所有数据点低维特征空间的分布都会改变.经过计算DB指标可知,数据点在三维特征空间中的最佳聚类数为9.通过对比各簇质心点,发现簇1为拥有高DNS查询总次数、DNS查询次数峰值以及非法域名比例的疑似异常簇.簇9内数据点数为221,这是因为部分正常的源IP多维特征与模拟的攻击源IP相似.
为了避免这种把正常源IP误判为异常情况发生,把连续多个时段出现频率较高的簇内疑似异常源IP与疑似异常簇的源IP作为最终的异常源IP.
最后,将笔者提出的DNS异常检测算法与文献[4-5]中的现有异常检测算法进行对比实验,如表 2所示.其中,文献[4]中的W-Kmeans算法即是对各个特征的初始权重取值,再进行K-means处理,以实现将各源IP分为异常簇与正常簇的目的;文献[5]中的基于相对密度的异常检测算法即是直接计算各源IP的相对密度,将相对密度低的源IP视为异常源IP.
|
|
表 2 不同检测算法运行结果对比 |
由表 2可知,在运行时间上,虽然W-Kmeans算法运行时间最短,但在每次检测时都需要人为调整各个特征的初始权重取值以及检测阈值,故其检测的实际时间成本较高;本文算法与相对密度算法在运行时间中表现相当.在检测异常源IP数上,由于W-Kmeans算法与相对密度算法是直接基于特征数值的检测,故对于特征维数数值明显异常源IP有着较好的检测效果,但无法检测出特征数值与正常值相差较小的异常源IP;而本文算法通过降维处理提取有效信息以及对聚类后簇内异常源IP的检测,故能够检测出隐藏的异常源IP.
综上可知,笔者提出的DNS异常检测算法相较于现有算法有着较为优异的表现.此外,本文算法还可以通过可视化呈现的方式,进一步分析数据分布的特点.
3 结束语提出了一种利用低维可视化与数据点可信度相结合的分析算法.先对DNS查询日志提取统计属性特征,再进行降维及聚类处理,在低维空间下对同簇数据点采取异常点检测的方法与对异簇间数据点的总体特征进行分析以检测出异常的源IP.采用真实的骨干网的DNS查询日志数据来验证异常源IP检测算法.经过实验分析可以发现,低维空间中相邻的节点往往具有显著的关联关系,以此为基础利用周围密度与总体特征相结合可检测出DNS查询中的异常源IP.
| [1] |
Jung J Y, Sit E, Balakrishnan H, et al. DNS performance and the effectiveness of caching[J]. IEEE/ACM Transactions on Networking, 2002, 10(5): 589-603. DOI:10.1109/TNET.2002.803905 |
| [2] |
Shan Guihua, Wang Yang, Xie Maojin, et al. Visual detection of anomalies in DNS query log data[C]//IEEE Pacific Visualization Symposium. New York: IEEE Press, 2014: 258-261.
|
| [3] |
林成虎, 李晓东, 金键, 等. 基于W-Kmeans算法的DNS流量异常检测[J]. 计算机工程与设计, 2013, 34(6): 2104-2108. Lin Chenghu, Li Xiaodong, Jin Jian, et al. DNS traffic anomaly detection based on W-Kmeans algorithm[J]. Computer Engineering and Design, 2013, 34(6): 2104-2108. DOI:10.3969/j.issn.1000-7024.2013.06.039 |
| [4] |
王靖云, 史建焘, 张兆心, 等. 基于相对密度的DNS请求数据流源IP异常检测算法[J]. 高技术通讯, 2016, 26(10-11): 849-856. Wang Jingyun, Shi Jiantao, Zhang Zhaoxin, et al. An algorithm for detection of source IP anomalies in DNS query based on relative density[J]. High Technology Letters, 2016, 26(10-11): 849-856. |
| [5] |
马云龙, 姜彩萍, 张千里, 等. 基于IPFIX的DNS异常行为检测方法[J]. 通信学报, 2014, 35(增刊1): 5-9. Ma Yunlong, Jiang Caiping, Zhang Qianli, et al. DNS abnormal behavior detection based on IPFIX[J]. Journal on Communications, 2014, 35(Sup1): 5-9. |
| [6] |
周昌令, 栾兴龙, 肖建国. 基于深度学习的域名查询行为向量空间嵌入[J]. 通信学报, 2016, 37(3): 165-174. Zhou Changling, Luan Xinglong, Xiao Jianguo. Vector space embedding of DNS query behaviors by deep learning[J]. Journal on Communications, 2016, 37(3): 165-174. |
| [7] |
Schölkopf B, Smola A J, Müller K R. Kernel principal component analysis[C]//7th International Conference on Artificial Neural Networks (ICANN). Berlin: Springer, 1997: 583-588.
|
| [8] |
Davies D L, Bouldin D W. A cluster separation measure[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 224-227. |
| [9] |
Jenssen R. Kernel entropy component analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 847-860. DOI:10.1109/TPAMI.2009.100 |


