2. 重庆邮电大学 移动通信技术重点实验室, 重庆 400065
针对第5代移动通信系统(5G)网络切片映射过程中,在满足系统时延要求的情况下,使资源调度最优化的问题,提出了一种基于时延感知的5G网络切片节点和链路映射成本最小化算法.该算法在网络功能虚拟化管理和编排器及各网络功能服务器处建立两级队列动态调度模型,感知系统中当前队列积压状态并进行动态调度,使系统队列积压始终维持在稳定的较小值,采用Lyapunov随机优化方法,实现对映射成本与系统时延的平衡控制.仿真结果表明,所提算法可在满足系统时延要求的同时,最优化资源调度,进而使得5G网络切片映射成本最小.
2. Key Laboratory of Mobile Communication Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
To optimize the resource scheduling while meeting the system delay requirement, the article proposes a delay-aware the fifth generation of mobile communications system (5G) network slicing node and link embedding algorithm in the process of 5G network slice embedding. The algorithm establishes a two-level queue dynamic scheduling model at the network functions virtualization management and orchestration and network functions virtualization servers. It realizes a current queue backlog in the system and carries on the dynamic scheduling, so that the system queue backlog is always maintained at the stable smaller value. The algorithm achieves the balance control between the embedding cost and the system delay by Lyapunov stochastic optimization method. The simulation results show that the algorithm can optimize the resource scheduling while satisfying the system delay requirement, and minimize 5G network slice embedding cost as well.
移动通信技术自20世纪80年代起发展十分迅速.为了第5代移动通信(5G,the fifth generation of mobile communications system)系统的部署,必然需要全新的相关技术实现无线网络资源的统一调度及管理[1],网络切片技术的提出可以有效地满足5G系统的需求,是实现5G网络的关键技术之一[2].虚拟网络映射(VNE,virtual network embedding)问题是5G网络切片中的关键问题. VNE问题是指在不改变底层物理网络的前提下,如何从物理资源中选择满足虚拟网络请求(VNR,virtual network request)的物理节点和链路,以使整个系统的映射成本最低,从而最大化网络运营商的收益[3].目前,已有不少学者针对VNE算法进行了研究[4-7],Wen等[7]基于长期演进(LTE, long term evolution)网络针对无线接入网中的层二提出了软件定义协议栈的概念,将层二中协议栈的每一个协议层进行模块化,并且认为每一个协议层模块可以单独作为一个虚拟化网络功能模块组件(VNFC,virtualized network function component)进行映射,同时将VNE问题转化为软件定义协议栈请求映射(SDPM,software defined protocol request mapping)问题,并提出了一种SDPM算法.
现有映射算法均没有考虑不同VNR在短时间内大量达到时,如何满足系统时延要求.因此,为了满足系统时延要求,保证系统性能,提出了基于时延感知的5G网络切片节点和链路映射(DANSNLE,delay-aware 5G network slicing node and link embedding)算法.
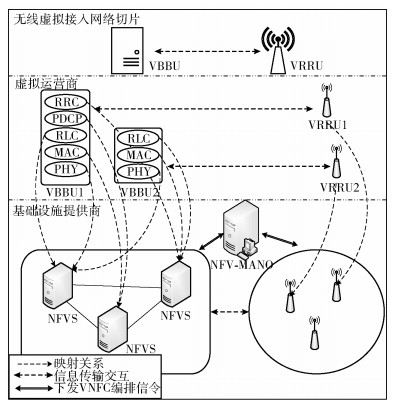
1 系统模型与问题描述 1.1 网络切片系统架构根据文献[7-8]提出了一种适合5G网络切片接入侧的系统架构,如图 1所示.
|
图 1 5G网络切片接入侧系统架构 |
整个架构分成3层,即无线虚拟接入网络切片层、虚拟运营商层和基础设施提供商层.其中,虚拟运营商提出VNR,且下发至网络功能虚拟化管理和编排器(NFV-MANO,network functions virtualization management and orchestration),基础设施提供商则通过NFV-MANO的控制根据不同的VNR实现不同VNFC的编排部署,进而形成不同的虚拟化室内基带处理单元(VBBU,birtual building baseband unit),并接入合适的虚拟化远端射频单元(VRRU,virtual remote radio unit),从而根据虚拟运营商的VNR构建完成不同需求的无线虚拟接入网络切片.
网络中网络功能虚拟化服务器(NFVS,network functions virtualization server)的集合为N={1, 2, …, f, …, j, …, n},不同VNFC种类的集合为M={1, 2, …, d, …, g, …, m},不同VNR类型的集合为I={1, 2, …, i},每台NFVS仅可支持运行有限的同一种VNFC,即
| $\sum\limits_{i \in \mathit{\boldsymbol{I}}} {{\beta _{idf}}} (t) \le Z,\forall d \in \mathit{\boldsymbol{M}},f \in \mathit{\boldsymbol{N}} $ | (1) |
其中:βidf(t)∈{0, 1},当且仅当VNRi中需要VNFCd,且该VNFCd映射至NFVSf时βidf(t)=1;Z为每台NFVS可支持运行同一种VNFC的最大数量.当VNFCd映射至NFVSf且VNFCg映射至NFVSj时,即实现虚拟链路到物理链路的映射,此时βidf(t)βigj(t)=1,同时针对任意一种VNR,其所需要的物理链路带宽不能超过任意两台NFVS间所提供的最大可用带宽上限,即
| $\sum\limits_{1 \le d < g \le \left| M \right|} {{\beta _{idf}}} (t){\beta _{igj}}(t){b_{dg}}(t) \le K, \forall i \in I, f, j \in \mathit{\boldsymbol{N}} $ | (2) |
其中:bdg(t)为2个VNFC之间虚拟链路所需要的带宽资源,K为任意两台NFVS间所提供的最大可用带宽上限.另外对于每一种VNR,应保证其所需要的VNFC均能够映射到NFVS上,即
| $\sum\limits_{f \in \mathit{\boldsymbol{N}}} {{\beta _{idf}}} (t) = \varepsilon _d^i(t), \forall i \in I, d \in M $ | (3) |
其中:εdi(t)为第i种VNR是否需要第d种VNFC,若需要则εdi(t)=1;否则εdi(t)=0.
1.2 两级队列调度模型结合排队论,在网络切片系统中NFV-MANO处及各NFVS处建立两级队列动态调度模型,使得NFV-MANO处及各NFVS处的VNR积压始终稳定在一个稳定范围内,保证用户的体验.
第1级队列动态调度发生在NFV-MANO处,该处队列状态转移方程为
| $\begin{array}{l} Q_{im}^M(t + 1) = \max \left[ {Q_{im}^M(t) + {\phi _i}(t)\varepsilon _m^i(t) - {\gamma _{im}}(t), 0} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall i \in I, m \in M \end{array} $ | (4) |
其中:QimM(t)为某一时隙内,NFV-MANO队列中来自虚拟运营商不同的VNRi中需要VNFCm的个数;ϕi(t)为某一时隙内到达NFV-MANO中类型为i的VNR个数,服从泊松分布,均值为λi,并假设存在达到峰值$\hat \phi $,使得$0 \le {\phi _i}(t) \le \hat \phi $, $\forall i \in I, \forall t \in T$成立;${\gamma _{im}}(t) = \sum\limits_{n \in N} {{\gamma _{imn}}} (t)$为第i种VNR中所需要的第m种VNFC映射请求路由的总个数,γimn(t)为系统中NFV-MANO处第i种VNR中所需要的第m种VNFC的映射请求路由至NFVSn,为了防止路由过程中的突发性,笔者认为$\sum\limits_{n \in N} {{\gamma _{imn}}} (t) < \hat N$.
第2级队列动态调度发生在每一台NFVS处,该处队列状态转移方程为
| $\begin{array}{*{20}{c}} {Q_{imn}^P(t + 1) = }\\ {\max \left[ {Q_{imn}^P(t) + {\gamma _{imn}}(t) - {\beta _{imn}}(t){S_{imn}}(t), 0} \right]}\\ {\forall i \in I, m \in M, n \in \mathit{\boldsymbol{N}}} \end{array} $ | (5) |
其中:QimnP(t)为某一时隙内NFVSn的队列中待映射的来自虚拟运营商的不同VNRi中的VNFCm个数;Simn(t)为系统中VNFCm在NFVSn中的服务速率,服从泊松分布,均值为κs.
根据式(4)、式(5)可得时隙t起始时刻队列为
| $Q(t) = \sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{m \in \mathit{\boldsymbol{M}}} {\left[ {Q_{im}^M(t) + \sum\limits_{n \in \mathit{\boldsymbol{N}}} {Q_{imn}^P} (t)} \right]} } $ | (6) |
对式(6)两端取期望可得时间平均队列积压为
| $\bar Q = \mathop {\lim\; \sup }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t \in \mathit{\boldsymbol{T}}} E [Q(t)] $ | (7) |
其中T为系统网络运行时间.时间平均队列积压是与系统时延相关的时间平均性能指标,因此,为了满足系统时延要求,保证系统稳定性,需满足
| $\bar Q < \infty $ | (8) |
结合上述分析与讨论,可以进一步得到5G网络切片架构中的映射成本模型,表示为
| $\begin{array}{*{20}{c}} {c(t) = \sum\limits_{i \in \mathit{\boldsymbol{I}}} {\left( {\sum\limits_{f, j \in \mathit{\boldsymbol{N}}} {\frac{1}{{N(M - 1)}}} \sum\limits_{1 \le d < g \le 1\left| \mathit{\boldsymbol{M}} \right|} {\left( {{\beta _{idf}}(t)c_f^d(t) + } \right.} } \right.} }\\ {{\beta _{igj}}(t)c_j^g(t)) + \sum\limits_{1 \le d < g \le |\mathit{\boldsymbol{M}}|} {{\beta _{idf}}} (t){\beta _{igj}}(t){c_{fj}}(t){b_{dg}}(t))} \end{array} $ | (9) |
其中:cfd(t)为某一时隙内VNFCd映射到NFVSf上时,NFVSf的租用价格,cfj(t)为某一时隙内物理链路单位带宽的租用价格;rc(t)为NFVS的剩余计算资源,为反映网络负载情况,定义cfd(t)与NFVS中的剩余计算资源成反比,记cfd(t)=σ/rc(t),σ为非零常数,rb(t)为物理链路中的剩余带宽资源,同样定义cfj(t)与物理链路中剩余的带宽资源成反比,记cfj(t)=ζ/rb(t),ζ为非零常数;每完成一次VNR的映射,均需要更新cfd(t)与cfg(t);1/N(M-1)仅为了消除物理节点重复计算.
进一步,对式(9)两端取期望,可得时间平均映射成本c为
| $\bar c = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t \in \mathit{\boldsymbol{T}}} E [c(t)] $ | (10) |
控制目标为最小化时间平均映射成本,因此将节点和链路映射与系统时延问题描述为一个时延约束下的映射成本最小化问题:
| $\begin{array}{l} \mathop {\min }\limits_{{\gamma _{imn}}, {\beta _{imn}}} \bar c\\ {\rm{s}}{\rm{.t}}.{\rm{C1}}:\bar Q < \infty \\ \;\;\;\;\;\;{\rm{C}}2:\sum\limits_{i \in I} {{\beta _{idf}}} (t) \le Z, \forall d \in \mathit{\boldsymbol{M}}, f \in \mathit{\boldsymbol{N}}\\ \;\;\;\;\;\;{\rm{C}}3:\sum\limits_{i \in \mathit{\boldsymbol{I}}} {{\beta _{igj}}} (t) \le Z, \forall g \in \mathit{\boldsymbol{M}}, j \in \mathit{\boldsymbol{N}}\\ \;\;\;\;\;\;{\rm{C4}}:\sum\limits_{1 \le d < g \le 1\left| \mathit{\boldsymbol{M}} \right|} {{\beta _{idf}}} (t){\beta _{igj}}(t){b_{dg}}(t)K, \forall i \in \mathit{\boldsymbol{I}}, f, j \in \mathit{\boldsymbol{N}}\\ \;\;\;\;\;\;{\rm{C}}5:\sum\limits_{f \in \mathit{\boldsymbol{N}}} {{\beta _{idf}}} (t) = \varepsilon _d^i(t), \forall i \in \mathit{\boldsymbol{I}}, d \in \mathit{\boldsymbol{M}}\\ \;\;\;\;\;\;{\rm{C}}6:\sum\limits_{j \in \mathit{\boldsymbol{N}}} {{\beta _{igj}}} (t) = \varepsilon _g^i(t), \forall i \in \mathit{\boldsymbol{I}}, g \in \mathit{\boldsymbol{M}}\\ \;\;\;\;\;\;{\rm{C}}7:{\beta _{igj}}(t), {\beta _{idf}}(t) \in \{ 0, 1\} , \forall i \in \mathit{\boldsymbol{I}}, g, d \in \mathit{\boldsymbol{M}}, j, f \in \mathit{\boldsymbol{N}} \end{array} $ | (11) |
该问题的目标是在满足系统队列稳定的前提下最小化映射成本,属于离散时间的随机动态规划问题.式(11)中约束条件分别根据式(1)~(3)、式(8)得出,其中限制条件C7保证了决策变量的二元性.
2 Lyapunov优化与DANSNLE算法流程 2.1 Lyapunov优化模型转化定义QM(t)=QimM(t)、QP(t)=QimnP(t)分别表示时隙t的起始时刻,NFV-MANO以及NFVS中的VNR队列长度;定义${\mathit{\mathbb{Q}}}(t) \buildrel \Delta \over = \left[{{\mathit{\boldsymbol{Q}}^{M}}(t); {\mathit{\boldsymbol{Q}}^p}(t)} \right]$,且定义Lyapunov函数以衡量系统在时隙t起始时刻的积压状况为
| $\begin{array}{*{20}{c}} {L(\mathbb{Q}(t)) = }\\ {\frac{1}{2}\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{m \in \mathit{\boldsymbol{M}}} {\left[ {{{\left( {Q_{im}^M(t)} \right)}^2} + \sum\limits_{n \in \mathit{\boldsymbol{N}}} {{{\left( {Q_{imn}^P(t)} \right)}^2}} } \right]} } } \end{array} $ | (12) |
可以发现,当L($\mathbb{Q}$(t))取值越小,则系统中队列积压越少.不失一般性,这里假设L($\mathbb{Q}$(0))=0.
定义Lyapunov漂移为相邻2个时隙Lyapunov函数之差的条件期望:
| $\Delta (\mathbb{Q}(t)) = E\{ L(\mathbb{Q}(t + 1)) - L(\mathbb{Q}(t))|\mathbb{Q}(t)\} $ | (13) |
根据Lyapunov随机优化理论的算法设计原则,NFV-MANO需要在每个时隙t的起始时刻决定VNR的路由行为γimn(t)和VNR的映射行为βimn(t).优化如下Lyapunov漂移与加权代价函数之和(DPP,drift-plus-penalty)的上界
| $\Delta (\mathbb{Q}(t)) = VE\{ c(t)|\mathbb{Q}(t)\} $ | (14) |
其中:V>0称为Lyapunov控制参数,用于控制Lyapunov漂移与即时代价函数之间的平衡关系.
定理1(漂移与加权代价函数之和的定界)在任意算法控制下,∀$\mathbb{Q}$(t), ∀t∈T,DPP具有如下上界:
| $\begin{array}{l} \begin{array}{*{20}{c}} {\Delta (\mathbb{Q}(t)) + VE\{ c(t)|\mathbb{Q}(t)\} \le B + VE\{ c(t)|\mathbb{Q}(t)\} + }\\ {\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{m \in \mathit{\boldsymbol{M}}} E } \left\{ {Q_{im}^M(t)\left[ {{\phi _i}(t)\varepsilon _m^i(t) - {\gamma _{im}}(t)} \right]|\mathbb{Q}(t)} \right\} + }\\ {\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{m \in \mathit{\boldsymbol{M}}} {\sum\limits_{n \in \mathit{\boldsymbol{N}}} E } } \left\{ {Q_{imn}^P(t)\left[ {{\gamma _{imn}}(t) - } \right.} \right.}\\ {\left( {{\beta _{imn}}(t){S_{imn}}(t)} \right)]|\mathbb{Q}(t)\} } \end{array}\\ \end{array} $ | (15) |
具体证明过程参见文献[9],其中
| $\begin{array}{*{20}{c}} {B = \frac{1}{2}\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{m \in \mathit{\boldsymbol{M}}} E } \left\{ {\left[ {{{\left( {{\phi _i}(t)\varepsilon _m^i(t)} \right)}^2} + } \right.} \right.}\\ {{\gamma _{im}}{{(t)}^2} - 2{\phi _i}(t)\varepsilon _m^i(t){\gamma _{im}}(t)]|\mathbb{Q}(t)\} + }\\ {\frac{1}{2}\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{m \in \mathit{\boldsymbol{M}}} {\sum\limits_{n \in \mathit{\boldsymbol{N}}} E } } \left\{ {\left[ {{\gamma _{imn}}{{(t)}^2} + {{\left( {{\beta _{imn}}(t){S_{imn}}(t)} \right)}^2} - } \right.} \right.}\\ {2{\gamma _{imn}}(t)\left( {{\beta _{imn}}(t){S_{imn}}(t)} \right)]|\mathbb{Q}(t)\} } \end{array} $ |
由于c(t)包含链路映射花费,且两节点确定一条链路,所以需成对考虑节点,将式(15)重新写为如下形式
| $\begin{array}{*{20}{c}} {\mathop{\rm sum}\nolimits} (t) = \\ V\left( {\sum\limits_{i \in I} {\left( {\sum\limits_{f, j \in N} {\frac{1}{{N(M - 1)}}} } \right.} } \right.\sum\limits_{1 \le d < g \le |\boldsymbol{M}|} {\left( {{\beta _{idf}}(t)c_f^d(t) + } \right.} \\ {\beta _{igj}}(t)c_j^g(t)) + \\ \sum\limits_{1 \le d < g \le \left| \mathit{\boldsymbol{M}} \right|} {{\beta _{idf}}(t){\beta _{igj}}(t){c_{fj}}(t){b_{dg}}(t))) + } \\ \sum\limits_{i \in I} {\frac{1}{{M - 1}}} \sum\limits_{1 \le d < g \le |\boldsymbol{M}|} {\left\{ {Q_{id}^M(t)\left[ {{\phi _i}(t)\varepsilon _d^i(t) - {\gamma _{id}}(t)} \right] + } \right.} \\ Q_{ig}^M(t)\left[ {{\phi _i}(t)\varepsilon _g^i(t) - {\gamma _{ig}}(t)} \right]\} + \\ \sum\limits_{i \in I} {\frac{1}{{N(M - 1)}}} \sum\limits_{f, j \in \mathit{\boldsymbol{N}}} {\sum\limits_{1 \le d < g \le \left| {\boldsymbol{M}} \right|} {\left\{ {Q_{idf}^P(t)\left[ {{\gamma _{idf}}(t) - } \right.} \right.} } \\ \left( {{\beta _{{{idf}}}}(t){S_{idf}}(t)} \right)] + Q_{igj}^P(t)\left[ {{\gamma _{igj}}(t) - } \right.\\ \left( {{\beta _{igj}}(t){S_{igj}}(t)} \right)]\} ) \end{array} $ | (16) |
其中:1/M-1与1/N(M-1)为消除重复计算.
经过转化后的最小化映射成本模型为
| $\begin{array}{l} \mathop {\min }\limits_{\gamma imn, \beta imn} {\mathop{\rm sum}\nolimits} (t)\\ {\rm{s.t.}}{\rm{C1}}:0 \le \sum\limits_{f \in \mathit{\boldsymbol{N}}} {{\gamma _{idf}}} (t) < \hat N, \forall i \in I, d \in M\\ \;\;\;\;\;{\rm{C}}2:0 \le \sum\limits_{g \in \mathit{\boldsymbol{N}}} {{\gamma _{igj}}} (t) < \hat N, \forall i \in I, j \in M\\ \;\;\;\;\;{\rm{C}}3:\sum\limits_{i \in \mathit{\boldsymbol{I}}} {{\beta _{idf}}} (t) \le Z, \forall d \in M, f \in N\\ \;\;\;\;\;{\rm{C}}4:\sum\limits_{i \in \mathit{\boldsymbol{I}}} {{\beta _{igj}}} (t) \le Z, \forall g \in M, j \in N\\ \;\;\;\;\;{\rm{C}}5:\sum\limits_{1 \le d < g \le \left| M \right|} {{\beta _{idf}}} (t){\beta _{igj}}(t){b_{dg}}(t) \le K, \\ \;\;\;\;\;\;\;\;\;\;\forall i \in I, f, j \in N\\ \;\;\;\;\;{\rm{C}}6:\sum\limits_{f \in \mathit{\boldsymbol{N}}} {{\beta _{idf}}} (t) = \varepsilon _d^i(t), \forall i \in I, d \in M\\ \;\;\;\;\;{\rm{C}}7:\sum\limits_{j \in \mathit{\boldsymbol{N}}} {{\beta _{igj}}} (t) = \varepsilon _g^i(t), \forall i \in I, g \in M\\ \;\;\;\;\;{\rm{C}}8:{\gamma _{idf}}(t), {\gamma _{igj}}(t), {\beta _{idf}}(t), {\beta _{igj}}(t) \in \{ 0, 1\} , \\ \;\;\;\;\;\;\;\;\;\;\forall i \in I, g, d \in M, j, f \in N \end{array} $ | (17) |
其中:限制条件C1与C2是为了限制VNR转移至NFVS的突发性,C8为了保证决策变量的二元性,其他限制条件与式(11)中限制条件物理意义相同.
忽略无关常量,对目标函数进行整理可得
| $\begin{array}{*{20}{c}} {{\mathop{\rm sum}\nolimits} (t) = }\\ {\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{1 \le d \le g \le \left| \mathit{\boldsymbol{M}} \right|} {\sum\limits_{f, j \in \mathit{\boldsymbol{N}}} {\left( {\frac{1}{N}\frac{1}{{(M - 1)}}\left( {V{\beta _{idf}}(t)c_f^d(t) + } \right.} \right.} } } }\\ {V{\beta _{igj}}(t)c_j^g(t) - Q_{idf}^P(t)\left( {{\beta _{idf}}(t){S_{idf}}(t)} \right) - }\\ {\begin{array}{*{20}{c}} {Q_{igj}^P(t)\left( {{\beta _{igj}}(t){S_{igj}}(t)} \right)) + V{\beta _{idf}}(t){\beta _{igj}}(t){c_{fj}}(t){b_{dj}}(t)) - }\\ {\sum\limits_{i \in \mathit{\boldsymbol{I}}} {\sum\limits_{1 \le d \le g \le \left| \mathit{\boldsymbol{M}} \right|} {\left( {\frac{1}{{(M - 1)}}\left( {Q_{id}^M(t){\gamma _{id}}(t) + Q_{ig}^M(t){\gamma _{ig}}(t)} \right) + } \right.} } }\\ {\sum\limits_{f, j \in \mathit{\boldsymbol{N}}} {\frac{1}{N}\frac{1}{{(M - 1)}}\left( {Q_{idf}^P(t){\gamma _{idf}}(t) + Q_{igj}^P(t){\gamma _{igj}}(t)} \right))} }\\ {} \end{array}} \end{array} $ | (18) |
不难看出,上述问题属于三维0-1二次规划问题,无法直接进行求解,因此根据决策变量γimn(t)及βimn(t)对最小化问题进行分解,将式(18)转化为如下两类|I|个二维0-1二次规划子问题.
1) NFV-MANO处VNR路由问题
| $\begin{array}{*{20}{c}} {\mathop {\min }\limits_{\gamma imn} \sum\limits_{1 \le d \le g \le M} {\left( {\sum\limits_{f, j \in N} {\frac{1}{N}} \frac{1}{{(M - 1)}}\left( {Q_{idf}^P(t){\gamma _{idf}}(t) + } \right.} \right.} }\\ {Q_{igj}^P(t){\gamma _{igj}}(t)) - \frac{1}{{(M - 1)}}\left( {Q_{id}^M(t){\gamma _{id}}(t) + } \right.}\\ {Q_{ig}^M(t){\gamma _{ig}}(t)))}\\ {} \end{array} $ | (19) |
2) NFVS处VNR映射问题
| $\begin{array}{*{20}{c}} {\mathop {\max }\limits_{{\beta _{imn}}} \sum\limits_{1 \le d \le g \le M} {\sum\limits_{f, j \in \mathit{\boldsymbol{N}}} {\left( {\frac{1}{N}\frac{1}{{(M - 1)}}\left( {Q_{idf}^P(t)\left( {{\beta _{idf}}(t){S_{idf}}(t)} \right) + } \right.} \right.} } }\\ {Q_{igj}^P(t)\left( {{\beta _{igj}}(t){S_{igj}}(t)} \right) - V{\beta _{idf}}(t)c_f^d(t) - }\\ {V{\beta _{igj}}(t)c_j^g(t)) - V{\beta _{idf}}(t){\beta _{igj}}(t){c_{fj}}(t){b_{dj}}(t))} \end{array} $ | (20) |
基于上述分析,提出了满足系统时延要求的DANSNLE算法,具体算法流程如算法1所示.
算法1 基于时延感知的5G网络切片节点和链路映射算法
输入:M,N,I,T,V.
输出:γimn(t),βimn(t),c(t)
1 初始化:t←0,QimM(t)←0,QimnP(t)←0,rc(t),rb(t),σ,ζ.
2 while t≤T do
3 for i∈I do
4 cfd(t)=σ*./rc(t).
5 cfj(t)=ζ*./rb(t).
6 根据式(19)采用分支定界法得到γimn(t).
7 根据式(20)采用分支定界法得到βimn(t).
8 根据βimn(t)更新rc(t)及rb(t).
9 for m∈M do
10 根据式(4)更新QimM(t).
11 for n∈N do
12 根据式(5)更新QimnP(t).
13 end for
14 end for
15 end for
16 根据式(9)计算得到c(t).
17 t++.
18 end while
定理2(基于时延感知的5G网络切片节点和链路映射算法的理论性能)所提算法控制下的时间平均队列满足
| $\bar Q \le \frac{{B + V\hat c}}{{\rm{e}}} $ | (21) |
其中e为非零常数.与此同时,最优映射成本c*与所提算法控制下的成本c满足
| ${\bar c^{{\rm{ our }}}} \buildrel \Delta \over = \mathop {\lim \sup }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t \in T} E [c(t)] \le {\bar c^*} + \frac{B}{V} $ | (22) |
证明 运用文献[9]中的随机优化理论的标准结果得证.
3 仿真与分析利用matlab仿真工具对本文所提算法进行仿真验证.假设基础设施提供商拥有5台NFVS,每台NFVS均可运行4种不同类型的VNFC,且运行每种VNFC的最大数量服从均匀分布U(5, 10),每台NFVS通过物理链路两两互联,每条物理链路的最大容量服从均匀分布U(3, 8),设置σ=30,ζ=20,$\hat N = \hat \phi = 6$;假设虚拟运营商持续下发3种不同类型的VNR.每种类型VNR单位时隙内的到达率均服从参数为λi=2的泊松分布,而系统中不同NFVS针对每种VNFC的服务率则服从κs=4的泊松分布.为了验证本文算法的有效性和优越性,与文献[7]中的SDPM算法进行了比较分析;仿真持续200个时隙,每时隙长度为5 min.
1) 有效性评估
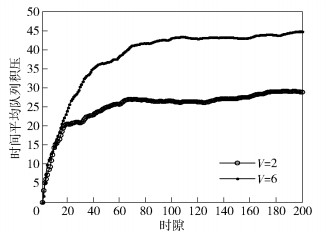
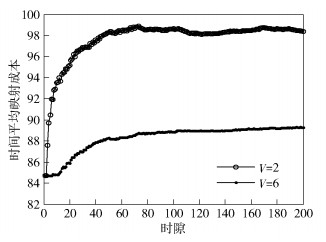
如图 2所示,随着仿真时隙的增加,时间平均队列积压起初迅速增加,随后趋于稳定,这也说明笔者所提的DANSNLE算法可以有效保证系统队列稳定性,满足系统时延要求,这一趋于稳定的趋势也与定理2中的式(21)的表述一致.如图 3所示,随着仿真时隙的增加,时间平均映射成本起初也会迅速增加,但最终仍会趋于一个稳定值,与定理2中的式(22)表述一致.
|
图 2 时间平均队列积压与时隙的关系 |
|
图 3 时间平均映射成本与时隙的关系 |
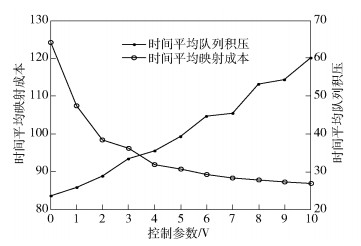
如图 4所示,当控制参数V的取值从0增大到10时,系统的平均队列积压Q由23.58增大到60.18,增幅达155.22%;同时,系统的平均映射成本c由124. 23降低到86. 81,降幅达30.12%,与定理2的表述相吻合,进而验证了c和Q之间存在[B(1/V), B(V)]平衡关系.
|
图 4 时间平均队列积压及时间平均映射成本与控制参数V的关系 |
2) 性能对比分析
所提DANSNLE算法与SDPM算法主要从时间平均队列积压与时间平均映射成本两方面进行性能对比分析.
如图 5所示,当VNR的到达率λi大于部分NFVS的服务速率Simn(t)时,DANSNLE算法相比于SDPM算法可以明显控制时间平均队列积压.这是因为DANSNLE算法在进行映射时,综合考虑了系统的队列状态以及NFVS服务速率的差异性,尽可能地将VNR转移至队列状态较短的队列,或将VNFC优先映射至服务速率较大的NFVS,并在综合考虑以上因素的前提下,选择使得映射花费最小的NFVS完成最终映射;而SDPM算法忽略了队列状态与NFVS服务速率的差异性,仅考虑如何使得映射花费最小,因此当选择服务速率较小的NFVS进行映射时,其服务能力显然无法满足短时间内VNR的大量达到,且系统无法动态地调整映射结果,因此必然会使队列积压严重,从而增大系统时延,影响用户体验.
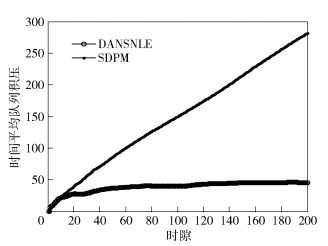
|
图 5 不同映射算法的时间平均队列积压比较 |
如图 6所示,DANSNLE算法因为综合考虑了队列状态与NFVS服务速率的差异性,所以在进行映射时,较SDPM算法相比,在映射成本最小化方面并不一定是最优结果,正与定理2的式(22)表述形式相吻合.通过图 5与图 6的对比分析,当系统队列趋于稳定时,SDPM算法下系统的时间平均映射成本为84.70,DANSNLE算法下系统的时间平均映射成本为88.25,DANSNLE算法较SDPM算法仅需增大4.19%的映射成本便可显著减少系统队列积压,进而满足系统时延要求.
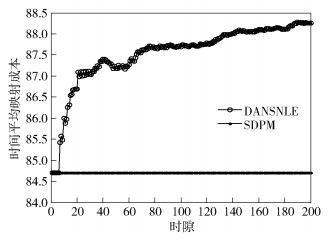
|
图 6 不同映射算法的时间平均映射成本比较 |
结合5G网络的最新需求,从资源调度最优化,进而最小化映射成本的角度,对5G网络切片中VNFC到NFVS的映射问题进行了研究,提出了基于时延感知的5G网络切片节点和链路映射算法;同时从理论上证明了该算法可以在时间平均映射成本以及时间平均队列积压之间实现可控平衡.仿真结果证明,本文算法可以显著减少系统队列积压,满足系统时延要求,进而虚拟运营商通过本文算法实现映射成本以及系统时延之间的灵活控制.
| [1] |
Benchaabene Y, Boujnah N, Zarai F. 5G Cellular: survey on some challenging techniques[C]//International Conference on Parallel and Distributed Computing, Applications and Technologies (PDCAT). New York: IEEE Press, 2017: 348-353.
|
| [2] |
Foukas X, Patounas G, Elmokashfil A, et al. Network slicing in 5G:survey and challenges[J]. IEEE Communications Magazine, 2017, 55(5): 94-100. DOI:10.1109/MCOM.2017.1600951 |
| [3] |
Cai Zhiping, Liu Fang, Xiao Nong, et al. Virtual network embedding for evolving networks[C]//2010 IEEE Global Telecommunications Conference. New York: IEEE Press, 2010: 1-5.
|
| [4] |
Gong Xiaoxue, Guo Lei, Shen Gangxiang, et al. Virtual network embedding for collaborative edge computing in optical-wireless networks[J]. Journal of Lightwave Technology, 2017, 35(18): 3980-3990. DOI:10.1109/JLT.2017.2703311 |
| [5] |
Riggio R, Bradai A, Harutyunyan D, et al. Scheduling wireless virtual networks functions[J]. IEEE Transactions on Network and Service Management, 2016, 13(2): 240-252. DOI:10.1109/TNSM.4275028 |
| [6] |
Zhu Lei, Zhang Zhi Zhong, Feng Lin Lin. Wireless virtual network embedding algorithm through topology awareness[C]//16th International Conference on Optical Communications and Networks (ICOCN). New York: IEEE Press, 2017: 7-10.
|
| [7] |
Wen Ruihan, Feng Gang, Tan Wei, et al. Protocol function block mapping of software defined protocol for 5G mobile networks[J]. IEEE Transactions on Mobile Computing, 2018, 17(97): 1651-1665. |
| [8] |
Herrera J G, Botero J F. Resource allocation in NFV:a comprehensive survey[J]. IEEE Transactions on Network and Service Management, 2016, 13(3): 518-532. DOI:10.1109/TNSM.2016.2598420 |
| [9] |
NEELY M J. Stochastic network optimization with application to communication and queueing systems[M]. Williston: Morgan and Claypool, 2010.
|


