2. 华侨大学 厦门市移动多媒体通信重点实验室, 福建 厦门 361021
为适应动态信道条件,提高传输可靠性,基于增量冗余混合自动重传请求和码率兼容低密度奇偶校验码(RC-LDPC),研究了多中继选择的速率自适应中继协作传输体制.针对中继节点的随机分布和特定分布,提出2种不同的中继选择协作方案,并给出了系统中断概率和吞吐量性能的表达式.数值分析和仿真结果表明,在中继节点的特定分布下引入中继之间的相互协作,可同时显著提高系统的中断概率和吞吐量性能.
2. Xiamen Key Laboratory of Mobile Multimedia Communications, Huaqiao University, Fujian Xiamen 361021, China
In order to adapt to dynamical channel conditions and improve the transmission reliability, rate-adaptive cooperative relay transmission schemes are investigated under multi-relay selection in combination with incremental redundancy hybrid automatic repeat request and rate-compatible low density parity check code (RC-LDPC). With respect to random and specific distributions of relay nodes, two different multi-relay selection protocols are proposed with deriving the expressions for the outage probability and throughput performances of the system. Both numerical and simulation results show that introducing a cooperation between the relays can significantly improve the system performance in both outage probability and throughput under the considered specific relay distribution.
协作中继通信的主要目的在于对抗无线信道的多径衰落,改善信息传输可靠性[1-2].中继选择是其性能改善的一个重要途径,机会式中继选择[3](ORS, opportunistic relay selection)方案基于R→D链路的信道状态信息(CSI, channel state information)选择1个最佳中继进行协作传输. Jiang等[4]对ORS方案做了改进:从译码集中选择N个最优中继进行协作转发.仿真结果表明,该改进的机会式多中继选择方案可显著降低系统的中断概率.引入中继之间(记为R→R)的协作传输也能增强信息传输可靠性,如完全分布式空时码(DSTC, distributed space-time code)协议充分利用中继间的协作传输,通过提高中继利用率来改善系统的分集增益[5];Wang等[6]证实了进一步考虑R→R链路的信道条件,在改善平均传输速率的同时还可降低系统的中断概率.总之,在多中继网络中,只要某个中继对源节点信息正确译码,通过引入中继之间的相互协作可提高目的节点处重构信号的保真度[7].
在实际通信中,采用固定码率传输很难取得预期设计效果.为了自适应信道变化,提高信息传输的有效性,可考虑采用码率兼容低密度奇偶校验(RC-LDPC, rate-compatible low density parity check)码[8-9].针对多中继网络提出一种基于机会式多中继选择的自适应中继协作体制.该体制在文献[4]的多中继选择方案基础上,增加了中继之间的相互协作,并联合应用混合自动重传请求(HARQ,hybrid automatic repeat request)技术和RC-LDPC码编码技术,实现不同码率的自适应传输.最后,针对所提体制推导系统的中断概率和吞吐量的表达式,分析信道衰落分布、最大重传次数等参数对中断概率、吞吐量性能的影响.
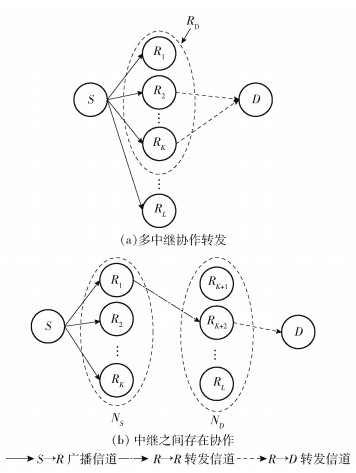
1 系统模型考虑图 1所示的中继协作模型,其中直传链路S→D由于距离过大而不予考虑. 2个传输阶段均采用基于RC-LDPC码的增量冗余HARQ方式,在不同信道条件下达到速率自适应传输的目的.根据图 1中继节点2种不同的位置分布,考虑2种中继选择协作方案.
|
图 1 多中继选择系统模型 |
方案1如图 1(a)所示,中继节点位置随机分布.令RD表示所有成功译码的中继节点构成的译码集.在第2阶段,从RD中选择K个中继节点进行协作传输,K=min{KT, |RD|},KT为上限阈值.
令M1和M2分别表示第1阶段和第2阶段的最大重传次数,则系统最大重传次数为M=M1+M2.在每次传输中,首先由源节点生成一个长度为N的母码码字,然后根据非贪婪打孔算法[10],按照码率递增次序依次生成M个序列xM, xM-1, …, x1, x0.各个序列的长度Nk表示删除的校验符号数,则
| ${N_k} = \frac{{N{r_M}\left( {{r_{k - 1}} - {r_k}} \right)}}{{{r_{k - 1}}{r_k}}}, 1 \le k \le M $ | (1) |
其中r为码率.最高码率r0的子码长为
| ${N_0} = N - \sum\limits_{k = 1}^M {{N_k}} $ | (2) |
方案1的协作传输过程如下:首先,由源节点向中继节点广播x0消息块,若无中继成功译码,则进行增量冗余重传,直至至少有1个中继成功译码或达到最大重传次数M1.在第k(0≤k≤M1)次重传中,各中继节点对k+1个接收消息块x0, x1, …, xk进行等效码率为rk的联合译码,若中继译码成功,则向S反馈以更新译码集RD.假定第1阶段的累计重传次数为q1,若q1=M1且|RD|=0,则系统发生中断;否则进入第2阶段.
在阶段2,分情况讨论:当1≤|RD|≤KT时,RD内所有中继均参与转发;当|RD|>KT时,根据最大信噪比的中继选择准则,选择KT个最优中继${\widetilde R_n}$,
| ${\widetilde R_n} = \left\{ \begin{array}{l} \mathop {\arg\max }\limits_{{R_i} \in {{\bf{R}}_D}}, \;\;\;\;n = 1\\ \mathop {\arg\max }\limits_{{R_i} \in {{\bf{R}}_D}\backslash \left\{ {{{\widetilde R}_1}, {{\widetilde R}_2}, \ldots , {{\widetilde R}_{n - 1}}} \right\}} {\gamma _{{R_i}D}}, \;\;\;\;2 \le n \le {K_T} \end{array} \right. $ | (3) |
中继转发链路以初始码率rq1进行HARQ传输,假定第2阶段的累计重传次数为q2,当q2=M2时,若D仍然译码失败,则系统发生中断.
1.2 特定分布的多中继选择协作协议方案2如图 1(b)所示,不失一般性,将靠近源节点的中继集记为NS={R1, R2, …, RK},而将靠近目的节点的中继集记为ND={RK+1, RK+2, …, RL}.在该分布下,引入中继之间的协作机制以增加中继利用率.因此,方案2与方案1的区别在于第2阶段.
在阶段2,首先从ND中选择1个最优中继Rb,
| ${R_b} = \mathop {\arg \max }\limits_{{R_i} \in {{\bf{N}}_D}} {\gamma _{{R_i}D}} $ | (4) |
然后,从RD中选择1~Rb的最优中继Ra,
| ${R_a} = \mathop {\arg \max }\limits_{{R_i} \in {{\bf{R}}_D}} {\gamma _{{R_i}{R_b}}} $ | (5) |
Ra以初始码率rq1向Rb进行HARQ传输,记Ra累计重传了q2(0≤q2≤M2)次,Rb累计重传了q3(0≤q3≤M2-q2)次,则当q2=M2,且Rb译码失败,或当q3=M2-q2,且D译码失败时,系统发生中断.
2 容量性能分析 2.1 中断概率的分析 2.1.1 中继随机分布的中断概率分析假设第1阶段源节点向中继节点广播传输了(q1+1)块数据(0≤q1≤M1),则中继Rn(n=1, 2, …, L)接收的每个符号的平均互信息为
| ${I_{{R_n}}}\left( {{q_1}} \right) = \frac{{\sum\limits_{k = 0}^{{q_1}} {{N_k}} {\mathop{\rm lb}\nolimits} \left( {1 + \gamma _{S{R_n}}^{(k)}} \right)}}{{\sum\limits_{k = 0}^{{q_1}} {{N_k}} }} $ | (6) |
同理,当第2阶段有K个中继参与协作转发时,目的节点D共接收(q2+1)K块数据(0≤q2≤M2),则D接收的每个符号的平均互信息
| ${I_D}\left( {{q_1},{q_2}} \right) = \frac{{\sum\limits_{k = 0}^{{q_2}} {\sum\limits_{n = 1}^K {{N_{{q_1} + k}}} } {\rm{lb}}\left( {1 + \gamma _{{R_n}^D}^{\left( {{q_1} + k} \right)}} \right)}}{{\sum\limits_{k = 0}^{{q_2}} {\left( {K{N_{{q_1} + k}}} \right)} }} $ | (7) |
式(6)和式(7)中的Nk表示系统第k次重传的码长,γij(k)=P|hij(k)|2/N0表示节点i、j间的瞬时信噪比,其中N0表示噪声功率谱密度,信道系数hij(k)服从均值为0、方差为Ωij的复高斯随机分布.
如果中继节点处的累积互信息量小于当前传输速率,则信息传输失败.记S→Rn链路通信成功的事件为An(n=1, 2, …, L),An(n=1, 2, …, L)为An(n=1, 2, …, L)的逆事件,则
| $P\left( {{{\bar A}_n}} \right) = P\left( {{I_{{R_n}}}\left( {{q_1}} \right) < {r_{{q_1}}}} \right) = {F_\gamma }\left( {\left\{ {\gamma _{S{R_n}}^{(k)}} \right\}_{k = 0}^{{q_1}}} \right) $ | (8) |
式(8)中的Fγ({γSRn(k)}k=0q1)表示多维随机变量(γSRn(0), γSRn(1), …, γSRn(q1))的联合概率分布函数.假设S→Rn每次传输经历的信道都是独立同分布准静态瑞利衰落信道,接收端采用最大比合并(MRC,maximal ratio combining)的方式,则根据文献[11],中继Rn处总的接收信噪比$\gamma _{{R_n}}^{{\rm{tot}}} = \sum\limits_{k = 0}^{{q_1}} {\gamma _{S{R_n}}^{(k)}} $服从Erlang分布,其分布函数为
| ${F_\gamma }(x) = 1 - \sum\limits_{m = 1}^{{q_1} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{x}{{\overline \gamma }}}}{\left( {\frac{x}{{\bar \gamma }}} \right)^{m - 1}} $ | (9) |
因此,
| $P\left(\overline{A}_{n}\right)=F_{\gamma}\left(\gamma_{\mathrm{th} 1}\right)=1-\sum\limits_{m=1}^{q_{1}+1} \frac{1}{(m-1) !} \mathrm{e}^{-\frac{\gamma_{\mathrm{thl}}}{\gamma_{S R_{n}}}}\left(\frac{\gamma_{\mathrm{th1}}}{\overline{\gamma}_{S R_{n}}}\right)^{m-1} $ | (10) |
| $P\left( {{A_n}} \right) = 1 - P\left( {{{\bar A}_n}} \right) $ | (11) |
其中γth1=2rq1-1.由于各链路经历的信道都是独立同分布的,所以P(A1)=…=P(AK)=P(A).
假设译码集的中继数为|RD|=K,则
| $P\left( {\left| {{R_D}} \right| = K} \right) = \sum\limits_{K = 0}^L {\left( {\begin{array}{*{20}{l}} L\\ K \end{array}} \right)} {(P(A))^K}{(P(\bar A))^{L - K}} $ | (12) |
根据K值的不同,系统的中断概率分情况讨论.
1) 当K>KT时,根据式(3)选择较优的KT个中继.由于中继选择的非线性,D处的Fγ(x)的闭合表达式不易直接求解.文献[12]中指出,当D端采用MRC合并时,γDtot的分布函数可由它的矩母函数(MGF, moment generating function)映射得到,且
| $\begin{array}{l} {P_{{\rm{ out }}}} = \frac{{{2^{ - W}}{{\rm{e}}^{A/2}}}}{{{\gamma _{{\rm{ th }}}}}}\sum\limits_{q = 0}^W {\left( {\begin{array}{*{20}{c}} W\\ q \end{array}} \right)} \sum\limits_{p = 0}^{P + q} {\frac{{{{( - 1)}^p}}}{{{\xi _p}}}} \times \\ \Re \left\{ {\frac{{{\mathscr{M}_{\gamma _D^{{\rm{ tot }}}}}\left( {\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}}}}}} \right)}}{{\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}}}}}}}} \right\} + E(A, P, W) \end{array} $ | (13) |
其中:$\Re \{ \cdot \} $表示实部,$\mathscr{M}_{\gamma_{D}^{\text { tot }}}\{\cdot\}$是D端合信噪比$\gamma _D^{{\rm{tot}}} = \sum\limits_{k = 0}^{{M_2}} {\gamma _D^{(k)}} $的MGF,$\gamma _D^{(k)} = \sum\limits_{n = 1}^{{K_T}} {\gamma _{{{\tilde R}_n}D}^{(k)}} $表示D端第k次接收信号的信噪比.当A=10ln10,P=21,W=15时,E(A, P, W) < 10-10,且
| ${\xi _p} = \left\{ {\begin{array}{*{20}{l}} {2, }&{p = 0}\\ {1, }&{p = 1, 2, \cdots } \end{array}} \right. $ |
| ${\mathscr{M}_{\gamma _D^{{\rm{tot}}}}}(s) = \prod\limits_{k = 0}^{{M_2}} {{\mathscr{M}_{\gamma _D^{(k)}}}} \left( {{s_k}} \right) $ | (14) |
| $\begin{array}{*{20}{c}} {{\mathscr{M}_{\gamma _D^{(k)}}}\left( {{s_k}} \right) = K\left( {K - {K_T}} \right)!\left( {\begin{array}{*{20}{c}} {K - 1}\\ {{K_T} - 1} \end{array}} \right){{\left( {\frac{1}{{1 + {s_k}{{\bar \gamma }_{{D_1}}}}}} \right)}^{{K_{{T^{ - 1}}}}}} \times }\\ {\sum\limits_{n = 0}^{K - {K_T}} {\frac{{{{( - 1)}^n}}}{{n!\left( {K - {K_T} - n} \right)!}}} \frac{1}{{\eta \left( {{s_k}} \right)}}} \end{array} $ | (15) |
且
| $\eta \left( {{s_k}} \right) = {K_T}\left( {1 + {s_k}{{\bar \gamma }_{{D_1}}}} \right) + n $ | (16) |
其中:sk=(A+2πjp)/2γth(k),γth(k)=2rq1+k-1,${\bar \gamma _{{D_1}}} = \sum\limits_{n = 1}^{{K_T}} {{{\bar \gamma }_{{{\tilde R}_n}D}}} /{K_T}$.
将式(14)~(16)代入式(13)可得
| $\begin{array}{*{20}{c}} {P\left( {{\rm{ outage }}|K > {K_T}} \right) = \frac{{{2^{ - W}}{{\rm{e}}^{A/2}}}}{{{\gamma _{{\rm{th2}}}}}}\sum\limits_{q = 0}^W {\left( {\begin{array}{*{20}{l}} W\\ q \end{array}} \right)} \sum\limits_{p = 0}^{P + q} {\frac{{{{( - 1)}^p}}}{{{\xi _p}}}} \times }\\ {\Re \left\{ {\frac{{{\mathscr{M}_{{\bf{ \pmb\gamma }}_D^{{\rm{ tot }}}}}\left( {\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}2}}}}} \right)}}{{\frac{{A + 2{\rm{ \mathsf{ π} j}}p}}{{2{\gamma _{{\rm{th2}}}}}}}}} \right\}} \end{array} $ | (17) |
其中γth2=2rq1+M2-1.
2) 当1≤K≤KT时,RD集里的所有中继均参与协作传输,此时$\gamma _D^{{\rm{tot}}} = \sum\limits_{k = 0}^{{M_2}} {\gamma _D^{(k)}} $服从Erlang分布.因此,
| $\begin{array}{*{20}{c}} {P\left( {{\rm{ outage }}|1 \le K \le {K_T}} \right) = }\\ {1 - \sum\limits_{m = 1}^{\left( {{M_2} + 1} \right)K} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th2}}}}}}{{\bar\gamma {D_2}}}}}{{\left( {\frac{{{\gamma _{{\rm{th}}2}}}}{{{{\bar \gamma }_{{D_2}}}}}} \right)}^{m - 1}}} \end{array} $ | (18) |
其中${\bar \gamma _{{D_2}}} = \sum\limits_{n = 1}^K {{{\bar \gamma }_{{R_n}D}}} /K$.
3) 当K=0时,系统发生中断是个必然事件,则
| $P({\rm{ outage }}|K = 0) = 1 $ | (19) |
综上,可求得系统中断概率为式(20)所示.
| $\begin{array}{*{20}{c}} {{P_{{\rm{ out }}}} = P\left( {K > {K_T}} \right)P\left( {{\rm{ outage }}|K > {K_T}} \right) + }\\ {P\left( {1 \le K \le {K_T}} \right)P\left( {{\rm{ outage }}|1 \le K \le {K_T}} \right) + }\\ {P(K = 0)P({\rm{ outage }}|K = 0) = }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\left\{ {\sum\limits_{K = {K_{{T^{ + 1}}}}}^L {\left( {\begin{array}{*{20}{l}} L\\ K \end{array}} \right)} {{\left[ {\sum\limits_{m = 1}^{{q_1} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\bar\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}}}{{\left( {\frac{{{\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}} \right)}^{m - 1}}} \right]}^K} \times } \right.} }\\ {{{\left[ {1 - \sum\limits_{m = 1}^{{q_1} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th1}}}}}}{{{\bar\gamma _{SR}}}}}}{{\left( {\frac{{{\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}} \right)}^{m - 1}}} \right]}^{\left( {L - K} \right)}} \times }\\ {(\frac{{{2^{ - W}}{{\rm{e}}^{A/2}}}}{{{\gamma _{{\rm{th}}2}}}}\sum\limits_{q = 0}^W {\left( {\begin{array}{*{20}{l}} W\\ q \end{array}} \right)} \sum\limits_{p = 0}^{P + q} {\frac{{{{( - 1)}^p}}}{{{\xi _p}}}} \times }\\ {\Re \left\{ {\frac{{{\mathscr{M}_{\gamma _D^{{\mathop{\rm tot}\nolimits} }}}\left( {\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}2}}}}} \right)}}{{\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}2}}}}}}} \right\}) + }\\ {\sum\limits_{K = 1}^{{K_T}} {\left( {\begin{array}{*{20}{l}} L\\ K \end{array}} \right)} {{\left[ {\sum\limits_{m = 1}^{{q_1} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}}}{{\left( {\frac{{{\gamma _{{\rm{th}}1}}}}{{{{\bar \gamma }_{SR}}}}} \right)}^{m - 1}}} \right]}^K} \times }\\ {{{\left[ {1 - \sum\limits_{m = 1}^{{q_1} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th1}}}}}}{{{\bar\gamma _{sR}}}}}}{{\left( {\frac{{{\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}} \right)}^{m - 1}}} \right]}^{\left( {L - K} \right)}} \times }\\ {\left[ {1 - \sum\limits_{m = 1}^{\left( {{M_2} + 1} \right)K} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th}}2}}}}{{{\bar\gamma {D_2}}}}}}{{\left( {\frac{{{\gamma _{{\rm{th}}2}}}}{{{{\bar \gamma }_{{D_2}}}}}} \right)}^{m - 1}}} \right]) \times }\\ {{{\left[ {1 - \sum\limits_{m = 1}^{{M_1} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}}}{{\left( {\frac{{{\gamma _{{\rm{th1}}}}}}{{{{\bar \gamma }_{SR}}}}} \right)}^{m - 1}}} \right]}^L}} \end{array} $ | (20) |
当中继节点满足特定分布时,引入中继间协作传输(对应图 1(b)).记Rb能正确译码的事件为Bq2事件,Bq2为Bq2的逆事件.
1) 当|RD|>1时,易求得
| $P\left( {\left| {{R_D}} \right| > 1} \right) = \sum\limits_{K = 2}^{\left| {{N_{\rm{S}}}} \right|} {\left( {\begin{array}{*{20}{c}} {\left| {{N_{\rm{S}}}} \right|}\\ K \end{array}} \right)} {(P(A))^K}{(P(\bar A))^{\left| {{N_{\rm{S}}}} \right| - K}} $ | (21) |
| $\begin{array}{*{20}{c}} {P\left( {{{\bar B}_{{q_2}}}||{R_D}| > 1} \right) = \frac{{{2^{ - W}}{{\rm{e}}^{A/2}}}}{{{\gamma _{{\rm{th}}3}}}}\sum\limits_{q = 0}^W {\left( {\begin{array}{*{20}{l}} W\\ q \end{array}} \right)} \sum\limits_{p = 0}^{P + q} {\frac{{{{( - 1)}^p}}}{{{\xi _p}}}} \times }\\ {\Re\left\{ {\frac{{{\mathscr{M}_{\gamma _{Rb}^{{\rm{tot}}}}}\left( {\frac{{A + 2{\rm{ \mathsf{ π} j}}p}}{{2{\gamma _{{\rm{th3}}}}}}} \right)}}{{\frac{{A + 2{\rm{ \mathsf{ π} j}}p}}{{2{\gamma _{{\rm{th3}}}}}}}}} \right\}} \end{array} $ | (22) |
其中:γth3=2rq1+q2-1,${{\mathscr M}_{\gamma _{{R_b}}^{{\rm{tot}}}}}(s) = \prod\limits_{k = 0}^{{q_2}} {{{\mathscr M}_{\gamma _{{{ R}_a}{R_b}}^{(k)}}}} \left({{s_k}} \right)$且${{\mathscr M}_{\gamma _{_{{R_a}{R_b}}}^{(k)}}}\left({{s_k}} \right) = {{\mathscr M}_{\gamma _D^{(k)}}}{\left. {\left({{s_k}} \right)} \right|_{K = \left| {{R_D}} \right|, {K_T} = 1}}$.
由重传规则可知,事件Bq2发生等价于联合事件Bq2-1Bq2发生,且P(B-1)=1.因此,
| $\begin{array}{*{20}{c}} {P\left( {{B_{{q_2}}}||{R_D}| > 1} \right) = }\\ {P\left( {{{\bar B}_{{q_2} - 1}}||{R_D}| > 1} \right) - P\left( {{{\bar B}_{{q_2}}}||{R_D}| > 1} \right)} \end{array} $ | (23) |
2) 同理,当|RD|=1时,易求得
| $P\left( {\left| {{R_D}} \right| = 1} \right) = \left( {\begin{array}{*{20}{c}} {\left| {{N_S}} \right|}\\ 1 \end{array}} \right)P(A){(P(\bar A))^{\left| {{N_s}} \right| - 1}} $ | (24) |
| $\begin{array}{*{20}{c}} {P\left( {{{\bar B}_{{q_2}}}||{R_D}| = 1} \right) = }\\ {1 - \sum\limits_{m = 1}^{{q_2} + 1} {\frac{1}{{(m - 1)!}}} {{\rm{e}}^{ - \frac{{{\gamma _{{\rm{th}}3}}}}{{{{\bar \gamma }_{{R_a}}}{R_b}}}}}{{\left( {\frac{{{\gamma _{{\rm{th}}3}}}}{{{{\bar \gamma }_{{R_a}{R_b}}}}}} \right)}^{m - 1}}} \end{array} $ | (25) |
最佳协作中继Rb累计重传(M2-q2)次后,目的节点仍然译码失败的概率为
| $\begin{array}{*{20}{c}} {P\left( {{\rm{ outage }}|{B_{{q_2}}}} \right) = \frac{{{2^{ - W}}{{\rm{e}}^{A/2}}}}{{{\gamma _{{\rm{th}}2}}}}\sum\limits_{q = 0}^W {\left( {\begin{array}{*{20}{l}} W\\ q \end{array}} \right)} \sum\limits_{p = 0}^{P + q} {\frac{{{{( - 1)}^p}}}{{{\xi _p}}}} \times }\\ {\Re \left\{ {\frac{{{\mathscr{M}_{{\gamma _{{D_1}}}}}\left( {\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}2}}}}} \right)}}{{\frac{{A + 2\pi {\rm{j}}p}}{{2{\gamma _{{\rm{th}}2}}}}}}} \right\}} \end{array} $ | (26) |
其中,${{\mathscr M}_{{\gamma _{{D_1}}}}}(s) = \prod\limits_{k = 0}^{{M_2} - {q_2}} {{{\mathscr M}_{\gamma _{{R_b}D}^{(k)}}}} \left({{s_k}} \right)$且${{\mathscr M}_{\gamma _{{R_b}D}^{\left(k \right)}}}\left({{s_k}} \right) = {{\mathscr M}_{\gamma _D^{\left(k \right)}}}{\left. {\left({{s_k}} \right)} \right|_{K = \left| {{N_D}} \right|, {K_T} = 1}}$.
将式(10)(11)、式(21)~(26)代入式(27)即可求出中断概率的理论值.
| $\begin{array}{*{20}{c}} {{P_{{\rm{out}}}} = P\left( {\left| {{R_D}} \right| > 1} \right)P\left( {{B_{{q_2}}}||{R_D}| > 1} \right)P\left( {{\rm{outage}}|{B_{{q_2}}}} \right) + }\\ {P\left( {\left| {{R_D}} \right| = 1} \right)P\left( {{B_{{q_2}}}||{R_D}| = 1} \right)P\left( {{\rm{outage}}|{B_{{q_2}}}} \right) + }\\ {P\left( {\left| {{R_D}} \right| > 1} \right)P\left( {{{\bar B}_{{M_2}}}||{R_D}| > 1} \right) + }\\ {P\left( {\left| {{R_D}} \right| = 1} \right)P\left( {{{\bar B}_{{M_2}}}||{R_D}| = 1} \right) + }\\ {P\left( {\left| {{R_D}} \right| = 0} \right)P\left( {{\rm{outage}}||{R_D}| = 0} \right) = }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\sum\limits_{{q_2} = 0}^{{M_2}} {\left[ {\sum\limits_{K = 2}^{|{N_S}|} {\left( {\begin{array}{*{20}{c}} {\left| {{N_S}} \right|}\\ K \end{array}} \right)} {{(P(A))}^K}{{(P(\bar A))}^{\left| {{N_S}} \right| - K}} \times } \right.} } }\\ {P\left( {{B_{{q_2}}}||{R_D}| > 1} \right)P\left( {{\rm{outage}}|{B_{{q_2}}}} \right) + }\\ {\left( {\begin{array}{*{20}{c}} {\left| {{N_S}} \right|}\\ 1 \end{array}} \right)P(A){{(P(\bar A))}^{\left| {{N_S}} \right| - 1}} \times }\\ {P\left( {{B_{{q_2}}}||{R_D}| = 1} \right)P\left( {{\rm{outage}}|{B_{{q_2}}}} \right)] + }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\left[ {\sum\limits_{K = 2}^{|{N_s}|} {\left( {\begin{array}{*{20}{c}} {\left| {{N_S}} \right|}\\ K \end{array}} \right)} {{(P(A))}^K}{{(P(\bar A))}^{\left| {{N_S}} \right| - K}} \times } \right.} }\\ {P\left( {{{\bar B}_{{M_2}}}||{R_D}| > 1} \right) + }\\ {\left( {\begin{array}{*{20}{c}} {\left| {{N_S}} \right|}\\ 1 \end{array}} \right)P(A){{(P(\bar A))}^{\left| {{N_s}} \right| - 1}}P\left( {{{\bar B}_{{M_2}}}||{R_D}| = 1} \right)] + }\\ {{{\left. {{{(P(\bar A))}^{\left| {{N_S}} \right|}}} \right|}_{{q_1} = {M_1}}}} \end{array} $ | (27) |
吞吐量定义为目的节点在整个信息传输过程当中成功接收的信息序列长度b与累计接收的平均序列长度N之比,单位为bit·s-1·Hz-1,其理论值为
| $\eta = b\left[ {1 - {P_{{\rm{ out }}}}} \right]/\bar N $ | (28) |
在中继随机分布下,令Ck表示源节点累计重传k次后译码集非空的事件,Dk表示目的节点第k次接收后正确译码的事件,Ck、Dk分别表示事件Ck、Dk的逆事件,Ntot1、Ntot2分别表示与事件Dk、Dk对应的接收序列长度.假设源节点累计重传了q1次,中继节点累计重传了q2次,则根据重传规则可得,D处累计接收的统计平均序列长度为
| $\bar N = P\left( {{C_{{q_1}}}} \right)P\left( {{D_{{q_2}}}|{C_{{q_1}}}} \right){N_{{\rm{tot1}}}} + P\left( {{C_{{q_1}}}} \right)P\left( {{{\bar D}_{{M_2}}}|{C_{{q_1}}}} \right){N_{{\rm{tot}}2}} $ | (29) |
| $P\left( {{D_{{q_2}}}|{C_{{q_1}}}} \right) = P\left( {{{\bar D}_{{q_2} - 1}}|{C_{{q_1}}}} \right) - P\left( {{{\bar D}_{{q_2}}}|{C_{{q_1}}}} \right) $ | (30) |
因此,式(29)可改写为式(31)所示.将式(10)~(12)、式(17)(18)、式(20)、式(31)代入式(28)即可求出方案1的吞吐量理论值.
同理,在中继特定分布下,可求得目的节点累计接收的平均序列长度N,如式(32)所示.将式(10)~(12)、式(21)~(27)、式(32)代入式(28)即可求出方案2的吞吐量的理论值.
| $\begin{array}{*{20}{c}} {\bar N = P\left( {{C_{{q_1}}}} \right)P\left( {{D_{{q_2}}}|{C_{{q_1}}}} \right){N_{{\rm{tot1}}}} + P\left( {{C_{{q_1}}}} \right)P\left( {{{\bar D}_{{M_2}}}|{C_{{q_1}}}} \right){N_{{\rm{tot}}2}} = }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\sum\limits_{{q_2} = 0}^{{M_2}} P } \left( {K > {K_T}} \right)\left[ {P{{\left. {\left( {{\rm{ outage }}|K > {K_T}} \right)} \right|}_{{M_2} = {q_2} - 1}} \times } \right.}\\ {\sum\limits_{k = 0}^{{q_2} - 1} {{N_{{q_1} + k}}} {K_T} - P{{\left. {\left( {{\rm{ outage }}|K > {K_T}} \right)} \right|}_{{M_2} = {q_2}}}\sum\limits_{k = 0}^{{q_2}} {{N_{{q_1} + k}}} {K_T}] + }\\ {P\left( {1 \le K \le {K_T}} \right)\left[ {P{{\left. {\left( {{\rm{ outage }}|1 \le K \le {K_T}} \right)} \right|}_{{M_2} = {q_2} - 1}} \times } \right.}\\ {\sum\limits_{k = 0}^{{q_2} - 1} {{N_{{q_1} + k}}} K - P{{\left. {\left( {{\rm{ outage }}|1 \le K \le {K_T}} \right)} \right|}_{{M_2} = {q_2}}}\sum\limits_{k = 0}^{{q_2}} {{N_{{q_1} + k}}} K] + }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\left[ {P\left( {K > {K_T}} \right)P\left( {{\rm{ outage }}|K > {K_T}} \right)\sum\limits_{k = 0}^{{M_2}} {{N_{{q_1} + k}}} {K_T} + } \right.} }\\ {P\left( {1 \le K \le {K_T}} \right)P\left( {{\rm{ outage }}|1 \le K \le {K_T}} \right)\sum\limits_{k = 0}^{{M_2}} {{N_{{q_1} + k}}} K]} \end{array} $ | (31) |
| $\begin{array}{*{20}{c}} {\bar N = P\left( {{C_{{q_1}}}} \right)P\left( {{B_{{q_1}}}|{C_{{q_1}}}} \right)P\left( {{D_{{q_3}}}|\left( {{B_{{q_2}}}, {C_{{q_1}}}} \right)} \right){N_{{\rm{tot1}}}}}\\ {P\left( {{C_{{q_1}}}} \right)P\left( {{B_{{q_2}}}|{C_{{q_1}}}} \right)P\left( {{{\bar D}_{{M_2} - {q_2}}}|\left( {{B_{{q_2}}}, {C_{{q_1}}}} \right)} \right){N_{{\rm{tot2}}}} = }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\sum\limits_{{q_2} = 0}^{{M_2}} {\sum\limits_{{q_3} = 0}^{{M_2} - {q_2}} {\left[ {P\left( {\left| {{R_D}} \right| > 1} \right)P\left( {{B_{{q_2}}}||{R_D}| > 1} \right) + } \right.} } } }\\ {P\left( {\left| {{R_D}} \right| = 1} \right)P\left( {{B_{{q_2}}}||{R_D}| = 1} \right)] \times }\\ {\left[ {P{{\left. {\left( {{\rm{ outage }}|{B_{{q_2}}}} \right)} \right|}_{{M_2} - {q_2} = {q_3} - 1}}\sum\limits_{k = 0}^{{q_3} - 1} {{N_{{q_1} + {q_2} + k}}} - } \right.}\\ {P{{\left. {\left( {{\rm{ outage }}|{B_{{q_2}}}} \right)} \right|}_{{M_2} - {q_2} = {q_3}}}\sum\limits_{k = 0}^{{q_3}} {{N_{{q_1} + {q_2} + k}}} ] + }\\ {\sum\limits_{{q_1} = 0}^{{M_1}} {\sum\limits_{{q_2} = 0}^{{M_2}} {\left[ {P\left( {\left| {{R_D}} \right| > 1} \right)P\left( {{B_{{q_2}}}||{R_D}| > 1} \right) + } \right.} } }\\ {P\left( {\left| {{R_D}} \right| = 1} \right)P\left( {{B_{{q_2}}}||{R_D}| = 1} \right)] \times }\\ {P\left( {{{\bar D}_{{M_2} - {q_2}}}|{B_{{q_2}}}} \right)\sum\limits_{k = 0}^{{M_2} - {q_2}} {{N_{{q_1} + {q_2} + k}}} } \end{array} $ | (32) |
仿真条件设置为:LDPC母码的码长和码率分别为N=1 008和rmin=0.5,L=5和KT=2,M=2(M1=1, M2=1)和M=4(M1=2, M2=2)对应的兼容码率分别为r={0.8, 0.75, 0.5}和r={0.8, 0.75, 0.7, 0.65, 0.5},仿真次数均为100万次.
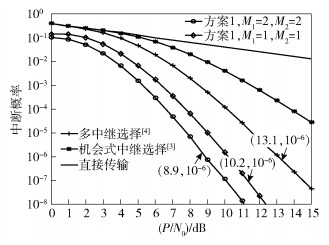
图 2所示为方案1与其他方案的中断概率性能,其中ΩSRn=1、ΩRnD=0.5.由图 2可知,方案1优于其他3种方案,且通过重传可以进一步降低系统的中断概率,在中断概率为10-6时,M=4相比于M=2与文献[4]方案分别有1.3 dB、4.2 dB的增益.
|
图 2 中继随机分布下的系统中断概率理论性能比较 |
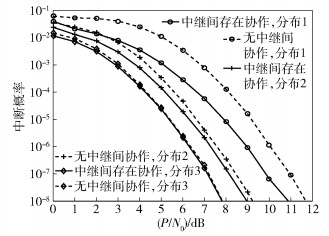
图 3所示为3种中继特定分布下的系统中断概率性能.其中,NS集、ND集的信道系数差异满足分布1>分布2>分布3.从图可知,引入中继间协作传输可以有效改善系统的中断概率性能,且当NS集、ND集的中继分布差异越大时,引入中继间协作传输改善的性能越明显.
|
图 3 不同中继特定分布下系统中断概率理论性能比较 |
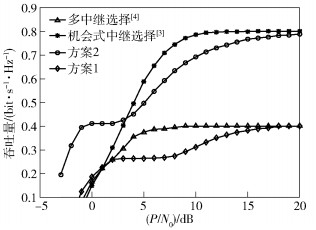
图 4所示为在图 3第2种中继特定分布下,本文2种方案与文献[3-4]方案的吞吐量理论性能比较.综合图 2~图 4的结果可知,2种方案在低信噪比区域同时具有中断概率、吞吐量的性能优势;在中等信噪比区域则分别以牺牲一定吞吐量性能为代价,获得中断概率性能优势;在高信噪比区域,保持中断概率性能优势的同时,各自逼近其理论极限性能.
|
图 4 吞吐量理论性能比较 |
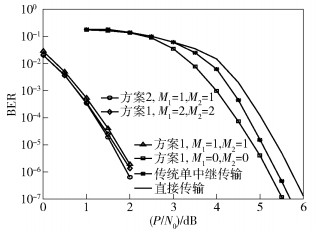
图 5所示为采用RC-LDPC编码传输时各方案的误比特率(BER,bit error ratio)性能比较,所提方案的BER性能明显优于其他2种方案,而且,通过重传可以进一步降低系统的BER.方案2由于引入中继间协作传输,BER性能提升更明显。
|
图 5 RC-LDPC编码传输的BER性能比较 |
提出一种基于RC-LDPC码的多中继选择算法,通过引入HARQ机制和中继间的协作传输,增加了中继协作的机会.在相同的条件下,与其他方案相比,本文方案可以有效降低系统的中断概率,在一定程度上提高系统吞吐量.
| [1] |
Hunter T E, Nosratinia A. Diversity through coded cooperation[J]. IEEE Transactions on Wireless Communications, 2006, 5(2): 283-289. DOI:10.1109/TWC.2006.1611050 |
| [2] |
Rossetto F, Zorzi M. Mixing network coding and cooperation for reliable wireless communications[J]. IEEE Wireless Communications, 2011, 18(1): 15-21. |
| [3] |
Bletsas A, Shin H, Win M Z. Cooperative communications with outage-optimal opportunistic relaying[J]. IEEE Transactions Wireless Communications, 2007, 6(9): 3450-3460. DOI:10.1109/TWC.2007.06020050 |
| [4] |
Jiang W, Kaiser T, Han Vinck A J. A robust opportunistic relaying strategy for cooperative wireless communications[J]. IEEE Transactions Wireless Communications, 2016, 15(4): 2642-2655. DOI:10.1109/TWC.2015.2506574 |
| [5] |
Tran L Q V, Berder O, Sentieys O. On the performance of distributed space-time coded cooperative relay networks based on inter-relay communications[EB/OL]. Lannion, France: Eurasip Joural on Wireless Communications and Networking, 2013(2013-10-03)[2018-04-05]. https://link.springer.com/article/10.1186%2F1687-1499-2013-239.
|
| [6] |
Wang H, Xu G S, Li M. A selection cooperation scheme with feedback and effective utilization of inter-relay links[J]. IEEE Wireless Communications Letters, 2016, 5(4): 428-431. DOI:10.1109/LWC.2016.2576449 |
| [7] |
Abou-Rjeily C, Haddad S. Inter-relay cooperation:a new paradigm for enhanced relay-assisted FSO communications[J]. IEEE Transactions on Communications, 2014, 62(6): 1970-1982. DOI:10.1109/TCOMM.2014.2316262 |
| [8] |
Ha J, Kim J, Klinc D, et al. Rate-compatible punctured low-density parity-check codes with short block lengths[J]. IEEE Transactions Information Theory, 2006, 52(2): 728-738. DOI:10.1109/TIT.2005.862118 |
| [9] |
Vellambi B N, Fekri F. Finite-length rate-compatible LDPC codes:a novel puncturing scheme[J]. IEEE Transactions on Communications, 2009, 57(2): 297-301. DOI:10.1109/TCOMM.2009.02.060098 |
| [10] |
Zhou L, Huang W C, Zhao R, et al. A non-greedy puncturing method for rate-compatible LDPC codes[J]. Journal of Communications and Networks, 2017, 19(1): 32-40. |
| [11] |
Ibe O. Fundamentals of applied probability and random processes[M]. Amsterdam, The Netherlands: Elsevier, 2005: 137.
|
| [12] |
Ko Y C, Alouini M S, Simon M K. Outage probability of diversity systems over generalized fading channels[J]. IEEE Transactions on Communications, 2000, 48(11): 1783-1787. DOI:10.1109/26.886467 |
| [13] |
Yilmaz F, Alouini M S. A unified MGF-based capacity analysis of diversity combiners over generalized fading channels[J]. IEEE Transactions on Communications, 2012, 60(3): 862-875. DOI:10.1109/TCOMM.2012.020912.100766 |
| [14] |
Xiao L, Dong X D. Unified analysis of generalized selection combining with normalized threshold test per branch[J]. IEEE Transactions Wireless Communications, 2006, 5(8): 2153-2163. DOI:10.1109/TWC.2006.1687731 |


