2. 北京理工大学 光电学院, 北京 100081
针对GM(1,1)算法求解发展系数和灰色作用量时受背景值影响的问题,提出一种回避背景值的辨识参数求解方法,避开背景值试算选取的步骤或选取不当造成预测精度低的问题;针对GM(1,1)模型预测时初始条件为固定值影响预测精度的问题,提出一种构建变权初始值的方法,避免预测精度受固定初始值的影响;针对传统灰色神经网络样本类型单一的问题,提出一种新的组合预测模型结构,突破了传统模型只依靠单一浸润线历史数据预测的局限,建立了基于改进灰色神经网络的浸润线预测模型.通过工程验证,该模型短期内对浸润线高度的变化预测效果较好.
2. College of Optoelectronics, Beijing Institute of Technology, Beijing 100081, China
During the process of calculation, the problem of GM(1, 1) algorithm that used to solve the development factor and the gray affections can be influenced by the background value. The identifying parameters method of avoiding background value was proposed for calculation. The problem of low prediction accuracy caused by the background value of the selected steps or improper selection was solved. The problem of initial condition with fixed value can affect the prediction accuracy when using the GM(1, 1) model predicts. The method of constructing the initial value with the variable weight was proposed. The impacts of the fixed initial value to the prediction accuracy was avoided. Aiming at the problem of single sample type of traditional grey neural network, a new combination forecasting model was proposed. To tackle the limitation of the traditional model to predict saturation line only rely on the data of history single sample type, and the prediction model of saturation line based on improving grey neural network is established. Through engineering verification, it is shown that the model effectively predict the change of the saturation line height in the short term.
尾矿库是存储固液混合态矿产废渣、具有高势能的人造泥石流危险源,其安全程度严重影响社会经济与生态环境[1].而浸润线作为尾矿库的生命线,其位置高低与尾矿库安全密切相关.准确掌握浸润线高度,对确保尾矿库正常运行至关重要.然而浸润线高度受多种因素影响,致使其高度呈非线性变化,为准确、有效预测浸润线高度及变化趋势带来困难[2].鉴于此,李全明等[3]利用模糊理论分析尾矿库失事概率,开发风险评估软件预测浸润线高度变化,有效决策坝体安全稳定性,但预测精度尚待提高.李刚[4]用灰色理论的方法研究坝体变形数据,建立坝体位移预测模型,预测坝体形变趋势,效果良好,但只是基于仿真,并未经过工程验证,而且预测精度有待提高.利用灰度模型GM(grey mode)针对小样本、贫信息数据的优势,结合BP网络非线性处理能力强的特点,建立了尾矿库浸润线预测模型,该模型仿真相对传统方法预测精度较高.
1 GM(1, 1)模型算法局限及优化灰色系统理论是由我国学者邓聚龙教授于1982年提出的[5],是将离散随机数变为较有规律的生成数,该生成数随机性被显著衰弱,建立起的微分方程形式的模型,这样便于对其变化过程进行研究和描述.
1.1 GM(1, 1)模型算法GM(1, 1)模型由一个单变量的一阶微分方程构成,用于复杂系统内某一主导因素特征值拟合和预测. GM(1, 1)模型为最基本GM,推导过程见文献[6].
设X(0)为原始正数据序列:
| ${X^{(0)}} = \left( {{x^{(0)}}(1), {x^{(0)}}(2), {x^{(0)}}(3), \cdots , {x^{(0)}}(n)} \right) $ | (1) |
设X(1)为X(0)的1-AGO序列:
| ${X^{(1)}} = \left( {{x^{(1)}}(1), {x^{(1)}}(2), {x^{(1)}}(3), \cdots , {x^{(1)}}(n)} \right) $ | (2) |
其中
设Z(1)是X(1)的紧邻均值序列:
| ${Z^{(1)}} = \left( {{z^{(1)}}(2), {z^{(1)}}(3), {z^{(1)}}(4), \cdots , {z^{(1)}}(n)} \right) $ | (3) |
其中
定义GM(1, 1)的基本形式为
| ${x^{(0)}}(k) + a{z^{(1)}}(k) = b $ | (4) |
其中:a、b为辨识参数,a为发展系数,反映待预测量
设
| $B\hat a = {Y_n} $ |
由最小二乘估计法求
| $\hat a = {\left( {{B^{\rm{T}}}B} \right)^{ - 1}}{B^{\rm{T}}}{Y_n} $ | (5) |
其中:
白化GM(1, 1)模型,其形式为
| $\frac{{{\rm{d}}{x^{(1)}}(t)}}{{{\rm{d}}t}} + a{x^{(1)}}(t) = b $ | (6) |
式(4)的时间响应序列为
| ${\hat x^{(1)}}(k + 1) = \left( {{x^{(0)}}(1) - \frac{b}{a}} \right){{\rm{e}}^{ - ak}} + \frac{b}{a} $ | (7) |
对式(7)做一次累减(1-IAGO),得到原始序列的预测值为
| $\begin{array}{*{20}{c}} {{{\hat x}^{(0)}}(k + 1) = {{\hat x}^{(1)}}(k + 1) - {{\hat x}^{(1)}}(k) = }\\ {\left( {1 - {{\rm{e}}^a}} \right)\left( {{x^{(0)}}(1) - \frac{b}{a}} \right){{\rm{e}}^{ - ak}}} \end{array} $ | (8) |
其中:
实践发现,GM(1, 1)模型的拟合或预测效果参差不齐,通过分析GM(1, 1)模型发现: 1)灰色预测模型的预测精度与被预测对象的递变规律以及数据序列的光滑度有关;2)灰色微分拟合法建立的离散拟合方程是一个近似差分方程,很难保证拟合方程与待拟合系统的微分方程严格近似.
由式(5)知,辨识参数的求解与背景值Z(1)密切相关.而原始定义中的背景值由紧邻均值得到,也可以采用权系数的方式求背景值.所以Z(1)求取方式不同时,辨识参数a、b值的大小就会有所变化.准确合理地a、b值能够提高模型序列的预测精度[6],因此,提出一种回避背景值的辨识参数求解方法,避免求解a、b时对背景值试算选取的步骤以及选取不当造成模型预测精度低的问题.
除此之外,由式(8)可知,原始序列预测值是在初始条件为
GM(1, 1)模型的优化过程主要分为以下2步:首先采用改进的欧拉公式回避背景值的求解,以得到辨识参数;再采用自适应构造法构造初始值,克服初始条件为原序列初始值时为模型预测带来预测偏差大的问题.
1) 结合改进的欧拉公式回避背景值求解辨识参数,过程如下.
先用欧拉公式求初步预测值
| ${\bar y_{n + 1}} = {y_n} + hf\left( {{x_n}, {y_n}} \right) $ | (9) |
其中: h为步长,h=xn+1-xn;yn+1的精度可能不够,采用梯形公式加以校正,梯形公式为
| ${y_{n + 1}} = {y_n} + \frac{h}{2}\left[ {f\left( {{x_n}, {y_n}} \right) + f\left( {{x_{n + 1}}, {y_{n + 1}}} \right)} \right] $ | (10) |
将式(10)代入式(11),
| $\left. \begin{array}{l} y_{n + 1}^{(0)} = {y_n} + hf\left( {{x_n}, {y_n}} \right)\\ y_{n + 1}^{(k + 1)} = {y_n} + \frac{h}{2}\left[ {f\left( {{x_n}, {y_n}} \right) + f\left( {{x_{n + 1}}, y_{n + 1}^{(k)}} \right)} \right], \\ \;\;\;\;\;\;\;k = 0, 1, 2, \cdots \end{array} \right\} $ | (11) |
得到校正值,即
| ${y_{n + 1}} = {y_n} + \frac{h}{2}\left[ {f\left( {{x_n}, {y_n}} \right) + f\left( {{x_{n + 1}}, {{\bar y}_{n + 1}}} \right)} \right] $ | (12) |
此时建立具有预测-校正功能的改进欧拉公式:
| $\left. \begin{array}{l} 预测:{y_{n + 1}} = {y_n} + hf\left( {{x_n}, {y_n}} \right)\\ 校正:{y_{n + 1}} = {y_n} + \frac{h}{2}\left[ {f\left( {{x_n}, {y_n}} \right) + f\left( {{x_{n + 1}}, {{\bar y}_{n + 1}}} \right)} \right] \end{array} \right\} $ | (13) |
将其改写为平均化形式:
| $\left. \begin{array}{l} {y_p} = {y_n} + hf\left( {{x_n}, {y_n}} \right)\\ {y_c} = {y_n} + hf\left( {{x_{n + 1}}, {y_p}} \right)\\ {y_{n + 1}} = \frac{1}{2}\left( {{y_p} + {y_c}} \right) \end{array} \right\} $ | (14) |
变换式(6),即
| $\frac{{{\rm{d}}{x^{(1)}}(t)}}{{{\rm{d}}t}} = b - a{x^{(1)}}(t) $ | (15) |
令
| $f\left( {t, {x^{(1)}}(t)} \right) = \frac{{{\rm{d}}{x^{(1)}}(t)}}{{{\rm{d}}t}} = b - a{x^{(1)}}(t) $ | (16) |
将(16)代入(14),得
| $\begin{array}{*{20}{c}} {{x^{(1)}}(t + 1) + \left( {2 - {a^2}{h^2} + ah} \right) = }\\ {{x^{(1)}}(t)(2 - ah) + 2bh - ab{h^2}} \end{array} $ | (17) |
因为x(1)(t+1)=x(1)(t)+x(0)(t+1),则
| ${x^{(0)}}(t + 1) = - {x^{(1)}}(t)\frac{{ah}}{{1 + ah}} + \frac{{bh}}{{1 + ah}} $ | (18) |
令
| $M = - \frac{{ah}}{{1 + ah}}, N = \frac{{bh}}{{1 + ah}} $ | (19) |
取h=1,所以只要求出M、N的值,就能求出a、b.将式(18)表示为
| $C\hat b = Y $ | (20) |
令
| $C = \left[ {\begin{array}{*{20}{c}} {{x^{(1)}}(1)}&1\\ {{x^{(1)}}(2)}&1\\ \vdots & \vdots \\ {{x^{(1)}}(n - 1)}&1 \end{array}} \right], \quad Y = \left[ {\begin{array}{*{20}{c}} {{x^{(0)}}(2)}\\ {{x^{(0)}}(3)}\\ \vdots \\ {{x^{(0)}}(n)} \end{array}} \right] $ |
通过最小二乘法得到M,N,即
| $\hat b = {\left( {{C^{\rm{T}}}C} \right)^{ - 1}}{C^{\rm{T}}}Y $ | (21) |
由于C中只涉及X(1),Y只涉及原始序列,只要求出M、N,再将M、N代入式(19),就可以得到a、b.此过程避开了背景值的求解得到了辨识参数.至此,回避背景值求解辨识参数的过程介绍完毕.
2) 提出构造自适应初始值
提出用λx(0)(1)代替x(0)(1),将初始条件设为
| $ \hat{x}^{(1)}(1)=x^{(1)}(1)=\lambda x^{(0)}(1) $ | (22) |
将式(22)代入式(7),得
| $ \hat{x}^{(1)}(1)=x^{(1)}(1)=\lambda x^{(0)}(1) $ | (23) |
将指标函数定义为
| $\begin{array}{*{20}{c}} {W = \sum\limits_{k = 1}^n {{{\left[ {{{\hat x}^{(1)}}(k) - {x^{(1)}}(k)} \right]}^2}} = }\\ {\sum\limits_{k = 1}^n {{{\left\{ {\left[ {\lambda {x^{(0)}}(1) - \frac{b}{a}} \right]{{\rm{e}}^{ - a(k - 1)}} + \frac{b}{a} - {x^{(1)}}(k)} \right\}}^2}} } \end{array} $ | (24) |
求取λ值时,将式(24)看作是W关于λ的函数.由于W为预测序列误差平方和,只要求得使W取最小值时的λ值,就能满足误差最小的目标,得到较小误差的预测值,过程如下:
| $\begin{array}{*{20}{c}} {\frac{{{\rm{d}}W}}{{{\rm{d}}\lambda }} = 2\sum\limits_{k = 1}^n {\left\{ {\left[ {\lambda {x^{(0)}}(1) - \frac{b}{a}} \right]{{\rm{e}}^{ - a(k - 1)}} + } \right.} }\\ {\frac{b}{a} - {x^{(1)}}(k)\} {x^{(0)}}(1){{\rm{e}}^{ - a(k - 1)}} = }\\ {2\left\{ {\lambda {{\left[ {{x^{(0)}}(1)} \right]}^2}\sum\limits_{k = 1}^n {{{\rm{e}}^{ - 2a(k - 1)}}} + } \right.}\\ {\begin{array}{*{20}{c}} {\frac{b}{a}{x^{(0)}}(1)\sum\limits_{k = 1}^n {{{\rm{e}}^{ - a(k - 1)}}} - }\\ {{x^{(0)}}(1)\sum\limits_{k = 1}^n {{x^{(1)}}} (k){{\rm{e}}^{ - a(k - 1)}} - }\\ {\frac{b}{a}{x^{(0)}}(1)\sum\limits_{k = 1}^n {{{\rm{e}}^{ - 2a(k - 1)}}} \} }\\ {} \end{array}} \end{array} $ | (25) |
设
令
| $\lambda A{x^{(0)}}(1) + \frac{b}{a}(B - A) - C = 0 $ | (26) |
解之,得
| $\lambda = \frac{{\frac{b}{a}(A - B) + C}}{{A{x^{(0)}}(1)}} $ | (27) |
W对λ的二阶导数为
| $\frac{{{{\rm{d}}^2}W}}{{{\rm{d}}{\lambda ^2}}} = 2{\left[ {{x^{(0)}}(1)} \right]^2}\sum\limits_{k = 1}^n {{{\rm{e}}^{ - 2a(k - 1)}}} > 0 $ | (28) |
由于式(28)恒大于0,式(26)成立时,W在式(27)下取得极小值,此时的λ值即为所求值,λx(0)(1)就可作式(8)中的初始值.
此时,将a、b及λ值代入式(8)中,得
| $\begin{array}{*{20}{c}} {{{\hat x}^{(0)}}(k + 1) = {{\hat x}^{(1)}}(k + 1) - {{\hat x}^{(1)}}(k) = }\\ {\left( {1 - {e^a}} \right)\left( {\lambda {x^{(0)}}(1) - \frac{b}{a}} \right){{\rm{e}}^{ - ak}}} \end{array} $ | (29) |
求解式(29),当k≤n,
将山东某尾矿库2号剖面3号监测点2015-06-15—2015-06-24每天10:00的浸润线高度作为样本数据(共10个)(见表 1),可以看出,采用振弦式渗压计自动监测的浸润线高度数据与人工监测数据较接近,可作为安全评价的样本数据.
|
|
表 1 某尾矿库主坝2号剖面3号监测点浸润线监测数据对比 |
1) 将表 1中前8组数据作为训练数据,后两组数据作为测试数据进行计算
| $\begin{array}{*{20}{c}} {{X^{(0)}} = (8.15, 8.35, 8.52, 8.85, 9.13, }\\ {9.22, 9.14, 8.95)}\\ {{X^{(1)}} = (8.15, 16.5, 25.02, 33.87, 43, 52.22, }\\ {61.36, 70.31)}\\ {{Z^{(1) = }}(12.325, 20.76, 29.445, 38.435, 47.61, }\\ {56.79, 65.835)} \end{array} $ |
由式(5)求得传统GM(1, 1)的a≈-0.013 5,b≈8.357 7.
2) 优化辨识参数a、b时,由式(22)可得M≈0.013 5,N≈8.416 4,将M,N代入式(20),得a≈-0.013 3,b≈8.304 2,将a、b和x(0)(1)代入式(9),求得优化辨识参数GM(1, 1)算法浸润线预测值,如表 2所示.此时的预测值仍以x(0)(1)作为初始值时得到的,并未涉及对初始值的优化,所以对比的只是优化辨识参数前后的效果.
|
|
表 2 GM(1, 1)模型优化前后预测值与原始值对比 |
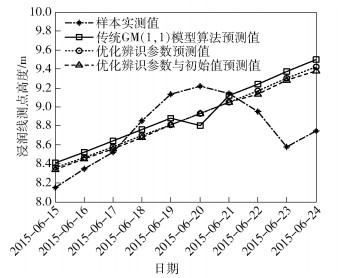
3) 初始值优化时,由第②步可知a≈-0.013 3,b≈8.304 2,所以A=8.80,B=8.38,C=330.65,将A、B、C代入式(28)得λ≈0.94,这时将a≈-0.013 3,b≈8.304 2,λ≈0.94代入式(30),计算得到新的初始值,求得优化辨识参数和初始值的GM(1, 1)模型预测值,如表 2所示. 图 1所示为GM(1, 1)优化前后浸润线预测值对比. 图 2所示为误差对比.
|
图 1 GM(1, 1)模型优化前后浸润线预测值对比 |
|
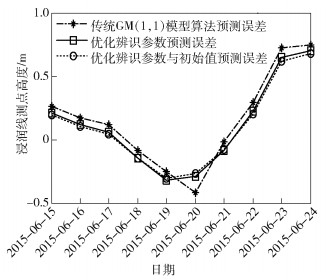
图 2 GM(1, 1)模型优化前后浸润线预测误差对比 |
由表 2可知,优化辨识参数的GM(1, 1)算法比传统GM(1, 1)算法有更好的预测效果,预测值的相对误差有所减小,平均相对误差有所降低,能更加逼近浸润线实测值,说明优化后求解的a、b值更准确;优化辨识参数和初始值GM(1, 1)模型的平均相对误差值最小,并且23、24日的预测值平均相对误差较前两者明显减小,说明优化初始值和辨识参数的GM(1, 1)模型有较好的预测能力.
由图 1可知,优化辨识参数和初始值GM(1, 1)模型预测值最接近原始值,说明优化方法得当,对传统算法性能有所改善.由图 2可以看出,经优化辨识参数和初始值的模型预测误差相比其他两者更小,更接近0值,在0值上下波动幅度小,说明辨识参数的求解以及初始值的设置更加合理,从而得到了较好的预测效果.
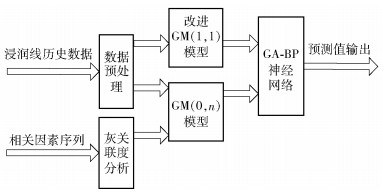
2 构建改进灰色神经网络尾矿库浸润线预测模型传统灰色神经网络模型,即GM(1, 1)模型浸润线预测时只使用了浸润线历史样本数据,采用了单变量主因素的主导思想预测因变量变化,导致样本数据种类较局限,不能准确反映相关因素所带来的变化[8-11].为了考虑不同因素对浸润线高度变化造成的影响,克服GM(1, 1)模型只依靠单一信息样本,即只采用历史浸润线数据变化来预测未来浸润线高度变化的时间序列模型所带来的预测精度低的问题,提出加入GM(0, N)模型. 图 3所示为改进的灰色神经网络组合模型结构图.
|
图 3 改进灰色神经网络模型结构 |
为了分析构建的浸润线预测模型是否合理,采用2015年6月山东某金矿尾矿库主坝2号剖面3号监测点实际浸润线历史数据及对应时间的其他监测量,如表 3所示.采用传统GM(1, 1)模型、传统BP神经网络模型、传统灰色神经网络模型以及尾矿库浸润线预测模型4种模型预测浸润线高度.
|
|
表 3 某尾矿库在线监测数据 |
表 4所示为4种模型对6月26~30日浸润线预测值.从表中可知,尾矿库浸润线预测模型的浸润线预测值与实际值较接近,其平均相对误差为1.55%,与各传统模型的相比浸润线预测值平均相对误差降低明显,满足了预期平均相对误差保持在3%以内的目标;浸润线预测值相对误差和传统模型的相比也有所降低,保证了浸润线预测值相对误差在5%以内的预期目标.
|
|
表 4 不同模型浸润线预测值对比 |
选择后验差对尾矿库浸润线模型精度等级进行检验,经计算,其均方差比值为0.324小于一级精度检验标准的0.35,在精度等级上达到了一级,满足精度要求.综上所述,所建立的尾矿库浸润线预测模型短期预测误差较小,精度等级较高,能较好预测短期内浸润线高度趋势.
4 结束语建立了改进灰色神经网络的尾矿库浸润线预测模型.该模型在尾矿库浸润线高度短期预测时精度较高,在短期预测中,尾矿库浸润线预测模型的浸润线预测值与实际值较接近,其平均相对误差为1.55%.与各传统模型相比,采用笔者提出的预测方法进行浸润线预测时,浸润线预测值平均相对误差降低明显,并且浸润线预测值平均相对误差能保持在3%以内,浸润线预测模型预测值相对误差能保持在5%以内,预测精度达到了一级标准,取得了较好的效果.
| [1] |
Ozcan N T, Ulusay R, Isik N S. A study on geotechnical characterization and stability of downstream slope of a tailings dam to improve its storage capacity (Turkey)[J]. Environmental Earth Sciences, 2013, 69(6): 1871-1890. DOI:10.1007/s12665-012-2016-1 |
| [2] |
Johari A, Javadi A A, Habibagahi G. Modelling the mechanical behaviour of unsaturated soils using a genetic algorithm-based neural network[J]. Computers and Geotechnics, 2011, 38(1): 2-13. DOI:10.1016/j.compgeo.2010.08.011 |
| [3] |
李全明, 张兴凯, 王云海, 等. 尾矿库溃坝风险指标体系及风险评价模型研究[J]. 水利学报, 2009, 40(8): 989-994. LI Quanming, Zhang Xingkai, Wang Yunhai, et al. Risk index system and evaluation model for failure of tailings dams[J]. Journal of Hydraulic Engineering, 2009, 40(8): 989-994. DOI:10.3321/j.issn:0559-9350.2009.08.014 |
| [4] |
李钢. 基于灰色系统理论的尾矿库坝体形变位移预测方法[J]. 中国安全生产科学技术, 2012, 8(4): 107-110. LI Gang. Research on the displacement forecasting methods of tailings dam deformation based on the gray system theory[J]. Journal of Safety Science and Technology, 2012, 8(4): 107-110. |
| [5] |
邓聚龙. 灰色控制系统[J]. 华中科技大学学报自然科学版, 1982(3): 11-20. Deng Julong. Grey control system[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 1982(3): 11-20. |
| [6] |
Farrokhzad F, Barari A, Choobbasti A J, et al. Neural network-based model for landslide suscepti-bility and soil longitudinal profile analyses:two case studies[J]. Journal of African Earth Sciences, 2011, 61(5): 349-357. DOI:10.1016/j.jafrearsci.2011.09.004 |
| [7] |
Hashemi M R, Hatam F. Unsteady seepage analysis using local radial basis function-based differential quadrature method[J]. Applied Mathematical Modelling, 2011, 35(10): 4934-4950. DOI:10.1016/j.apm.2011.04.002 |
| [8] |
Chemachema M. Output feedback direct adaptive neural network control for uncertain SISO nonlinear systems using a fuzzy estimator of the control error[J]. Neural Networks the Official Journal of the International Neural Network Society, 2012, 36(3): 25-34. |
| [9] |
Srinivasan K, Ng K C, Velasco S, et al. A corre-sponding states treatment of the liquid-vapor saturation line[J]. Journal of Chemical Thermodynamics, 2012, 44(1): 97-101. |
| [10] |
Xu Tongle, Wang Yingbo, Chen Kang. Tailings saturation line prediction based on genetic algorithm and BP neural network[J]. Journal of Intelligent & Fuzzy Systems, 2016, 30(4): 1947-1955. |
| [11] |
Qiao Jianyong. On the preimages of parabolic periodic points[J]. Nonlinearity, 2000, 13(3): 813-818. DOI:10.1088/0951-7715/13/3/316 |


