2. 重庆邮电大学 宽带接入网络研究所, 重庆 400065
提出了一种大规模机器类通信(mMTC)中基于功率控制的高可靠低迟延(URLL)上行无线资源优化方案.考虑时分双工蜂窝网络,设计了上行链路传输的反向功率控制方案,并导出了基于距离的链路可靠性函数;在此基础上,建立了上行无线资源优化模型,分析了链路可靠性函数的特性,并提出了一种基于黄金分割搜索最优的传输错误概率算法;给出了一种最小化系统所需的总带宽算法,可为每个用户分配多个子信道,用户通过判断信道增益是否超过门限值来选择子信道.仿真实验结果表明,新方案在迟延和可靠性的改进以及总带宽、功耗等方面的优势显著.
2. Institute of Broadband Access Networks, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
An optimal scheme of uplink resource allocation for ultra-reliable and low-latency (URLL) in massive machine type communications (mMTC) with power control is proposed. Considering time division duplexing (TDD) cellular networks, the reverse power control scheme of uplink transmission by using the distance measurement capability of multi-antenna TDD base station is designed and the link-based reliability function based on distance is derived. Further, the optimization model of uplink radio resources is built. Then the characteristic of the link reliability function is analyzed and an optimal transmission error probability algorithm based on golden section is proposed. Furthermore, an algorithm to minimize the total bandwidth required by the system is given. Multiple sub-channels may be assigned to each user, and the user selects the sub-channel by judging whether the channel gain exceeds the threshold. Finally, simulation experiments show the improvement of latency and reliability, as well as the performance advantages of total bandwidth, power consumption and so on.
面向2020年及未来,机器类通信(MTC, machine type communications)将会推动移动互联网应用爆发式增长[1],数以千亿的设备将接入网络,实现“万物互联”,也给下一代移动通信(5G)带来新的技术挑战[2]. MTC并发性地产生大量的短数据包类业务请求,而且部分应用场景还要求在支持大连接数的同时,进一步降低迟延、提高可靠性[3].超高可靠超低迟延通信(URLLC, ultra-reliable and low-latency communications)是许多MTC应用的一个重要特征,如工业自动化、公共安全、接触互联网、远程医疗、交通和车辆等[4].
在MTC中,相邻设备可能会长时间沉默,不需要为每个设备保留带宽;此外,在海量设备的情况下,也无法为每个设备保留带宽[5].针对5G中的MTC业务特征,一些学者开始探讨MTC的资源分配[6-11]等. Aijaz[6]针对触觉通信应用中的无线资源分配提出了一种低复杂度的联合上\下行链路调度算法,可满足触觉通信的实用需求,并优于经典算法. Chen等[7]研究了蜂窝中继网络的上行链路资源分配问题,有效地减少了能量的消耗,但未考虑公平分配问题. Aijaz等[8-9]提出LTE网络中用于M2M (machine-to-machine) /H2H(human-to-human)共存情景的无线资源分配模型,所提算法实现了总传输功率的最小化,并满足LTE用户(UE)和MTC设备(MTCD)的服务质量要求,并在服务质量(QoS,quality of service)的保证下上行链路资源分配设计. She等[10-11]在触觉网络中提出一种大规模机器类设备的上行传输设计,每个用户均采用最大发射功率来进行带宽分配.
但是,上述研究均未考虑在极低时延约束下,由于信道编码的有限块长,Shannon容量无法实现.而此时无线资源(发射功率和带宽)的最大可达率问题既非凸也非凹[12].如果用Shannon容量设计资源分配,则不能保证排队时延和时延违例率[13],从而不能满足高可靠性.笔者考虑高可靠低迟延要求下面向大规模MTC(mMTC)的无线资源管理问题,正如文献[4]指出,寻求低时延高可靠mMTC的最优资源分配策略更具挑战性.
基于以上分析,探讨了基于功率控制的mMTC中高可靠低迟延的上行无线资源优化问题,虽然She等[10-11]作了类似研究,但没有考虑功率控制[11],并且功率分配不够有效[10],在同样带宽资源传输功率较高,吞吐量反而较低.考虑时分双工(TDD,time division duplex)蜂窝网络,在超低时延性能约束下(1 ms)和每个MTC用户在最大传输功率限制下,首先,利用多天线TDD基站的测距(用户到基站的距离)能力,设计上行链路传输的反向功率控制方案,并导出了基于距离的链路可靠性函数;在此基础上,建立了上行无线资源优化模型,在确保总带宽达到了可靠性和迟延的性能前提下,通过优化子信道的数量、带宽以及每个用户的信道增益的门限值来最小化系统所需的总带宽;然后,分析了链路可靠性函数的特性,并提出了一种基于黄金分割的搜索最优的传输错误概率算法;进一步,给出了一种最小化系统所需的总带宽算法,可为每个用户分配多个子信道,用户通过判断信道增益是否超过门限值来选择子信道;最后,仿真实验结果显示,与文献[10-11]比较,本文方案和算法在迟延和可靠性的改进以及在功耗、能量效率、总带宽、吞吐量等性能上具有优势.
1 系统模型考虑一个基站的蜂窝系统,蜂窝基站天线的数目为Nt,K个单天线用户(UE和MTCD),所有用户在同一小区.假设用户在发送传输请求前都需要接入到基站中,用户产生的数据发送给基站,基站成功接收数据后发送给接收端.当用户设备有数据包传输时才分配带宽,基站给第k个用户分配Nk个子信道,每个子信道具有独立的信道增益.由于设备之间的干扰会导致QoS的严重恶化,所以假设并发传输的用户设备使用不同的子信道.
方案设计采用TDD方式.针对mMTC的上行链路传输优化设计,上行链路传输的步骤为:1)用户设备生成数据包;2)用户设备发出上行链路传输请求;3)传输授权和信道侦测(含测距);4)基站分配带宽;5)用户设备选择子道和数据包传输.
考虑频率—平坦衰落信道,用Bk表示分配给第k个用户设备的每个子信道的带宽,Wc表示信道相干带宽,当分配给每个用户的带宽小于信道相干带宽时它是有效的,即Bk < Wc能满足此要求.因为用户的数量很大,而所需的数据率很低(短数据包传输),在实际系统中可把频率离散成基本的带宽单元,例如正交频分复用系统中的子载波,每个子信道由多个带宽单元组成.通过调整子信道上的带宽单元数,可以改变每个子信道的带宽.为了实现频率分集增益,给第k个用户分配的Nk个子信道的瞬时信道增益是相互独立的,因此相邻子信道的频率间隔应大于信道相干带宽Wc.
第k个用户的平均信道增益表示为μk,第k个用户在第i个子信道上的瞬时信道增益表示为gk, i,对应的信道系数为hk~CN(0, 1)∈瘙綇Nt×1,即信道服从独立同分布的高斯分布,其均值为0,方差为1.
2 QoS约束分析QoS需求和约束反映每个用户的传输功率、每个数据包的上行传输延迟、系统总体可靠性.
2.1 传输功率控制为了降低传输功率,提高能量效率,在上行链路进行反向功率控制.设最大的发射功率为Pmax,给定用户k设备到基站的距离为rk,则用户设备的发射功率Pk表示为
| $ {P_k} = \left\{ {\begin{array}{*{20}{l}} {{\rho _0}r_k^\alpha , \;\;\;若{\rho _0}r_k^\alpha < {P_{\max }}}\\ {{P_{\max }}, \;\;\;其他} \end{array}} \right. $ | (1) |
其中:α>2为路径损耗指数,ρ0为基站所需的平均接收功率.
在TDD上行传输中采用反向功率控制,即当距离r满足
经过式(1)的反向功率控制,设每个数据包的大小为u bit,根据香农容量公式的无限长度编码,当基站完全知道μk和hk的信息时,第k个用户到基站在一帧内能传输的最大比特数为[15]
| $ s_{k} \approx \frac{T_{f} B_{k}}{\ln 2}\left\{\ln \left(1+\frac{\mu_{k} P_{k} g_{k}}{N_{0} B_{k}}\right)-\sqrt{\frac{V}{T_{f} B_{k}}} f_{Q}^{-1}\left(\varepsilon_{k}\right)\right\} $ | (2) |
其中:Pk表示第k个用户的发射功率,gk=hkHhk,[·]H表示共轭转置,N0表示单边信号噪声谱密度,fQ-1(x)表示Q函数的逆函数,V=1-
一帧中传输的符号数(也称为块长)是由带宽和传输持续时间根据lk=TfBk确定的,所以,对于充分大的lk,根据香农容量可以将式(2)近似为
| $ s_{k}^{\infty} \approx \frac{T_{f} B_{k}}{\ln 2} \ln \left(1+\frac{\mu_{k} P_{k} g_{k}}{N_{0} B_{k}}\right) $ | (3) |
为了满足系统的低迟延需求,不采用重传机制,所以每个数据包的上行链路数据传输应该在一帧内完成,且信道编码在每帧内完成.设信道相干时间表示为Tc,每个帧的持续时间为Tf,Dmax表示可允许的最大端到端迟延.由于传输数据包短和迟延低,所需的Dmax 和Tf都非常短,所以可以合理地假设Tc>Dmax ,Tf < Dmax .
第k个用户设备的QoS需求可定义为第k个用户上行传输时延Dk、第k个用户的传输错误率εk,其中k=1, 2, …, K,εmax 表示可允许最大的传输错误率.为了满足QoS需求,第k个用户设备必须满足Dk < Dmax 和εk < εmax .设每个TDD帧的持续时间为Tf,等同于系统的传输时间间隔.当忽略处理延迟时,控制信号和数据传输引起的延迟为Dk=3Tf每个数据包的传输时间应该小于一个帧的持续时间,这意味着在出现错误数据包的情况下,不允许在后续帧中重新传输.
2.3 可靠性约束为了满足系统的迟延需求,由于不能采用重传机制,考虑一个基于可实现速率的传输模型.该模型基于有限块长度信道编码,如果接收到的信噪比高于门限值,则可以成功地传输u bit的数据包,即sk∞≥u;否则,传输则不能成功.因此,如果瞬时信道增益gk高于门限值gkth,即sk≥u,则该数据包可以以1-εk的概率成功传输.否则,系统就丢掉数据包.在很高的信噪比下V≈1,把sk=u,V=1代入式(3)中得到信道增益门限的近似值为
| $ g_{k}^{\mathrm{th}} \approx \frac{N_{0} B_{k}}{\mu_{k} P_{k}}\left\{\exp \left[\frac{u \ln 2}{T_{f} B_{k}}+\sqrt{\frac{1}{T_{f} B_{k}}} f_{Q}^{-1}\left(\varepsilon_{k}\right)\right]-1\right\} $ | (4) |
把发射功率Pk代入式(4)中得到
| $ \begin{array}{c} g_k^{{\rm{th}}} = \\ \left\{ {\begin{array}{*{20}{l}} {\frac{{{N_0}{B_k}}}{{{\mu _k}{\rho _0}r_k^\alpha }}\left\{ {\exp \left[ {\frac{{u\ln 2}}{{{T_f}{B_k}}} + \sqrt {\frac{1}{{{T_f}{B_k}}}} f_Q^{ - 1}\left( {{\varepsilon _k}} \right)} \right] - 1} \right\}, 若{\rho _0}r_k^\alpha < {P_{\max }}}\\ {\frac{{{N_0}{B_k}}}{{{\mu _k}{P_{\max }}}}\left\{ {\exp \left[ {\frac{{u\ln 2}}{{{T_f}{B_k}}} + \sqrt {\frac{1}{{{T_f}{B_k}}}} f_Q^{ - 1}\left( {{\varepsilon _k}} \right)} \right] - 1}, 其他 \right\}, } \end{array}} \right. \end{array} $ | (5) |
考虑了传输模型考虑了当gk≥gkth时的传输错误概率,因此适用于在超高可靠性约束下设计的传输策略.第k个用户能成功传输的概率是至少有1个子信道的瞬时信道增益大于或等于gkth即
| $ \begin{array}{c} \Pr \left\{ {\bigcup\limits_{i = 1}^{{N_k}} {\left\{ {{g_{k, i}} \ge g_k^{{\rm{th}}}} \right\}} } \right\} = 1 - \prod\limits_{i = 1}^{{N_k}} {\Pr } \left\{ {{g_{k, i}} < g_k^{{\rm{th}}}} \right\} = \\ 1 - {\left[ {\int_0^{g_k^{{\rm{th}}}} {{f_g}} (x){d_x}} \right]^{{N_k}}} \end{array} $ | (6) |
其中:
用lk=1表示数据包能成功传输,lk=0表示不能成功传输,所以,数据包能成功传输的概率为
| $ \begin{array}{l} \Pr \left\{ {{l_k} = 1} \right\} = \Pr \left\{ {\bigcup\limits_{i = 1}^{{N_k}} {\left\{ {{g_{k, i}} \ge g_k^{{\rm{th}}}} \right\}} } \right\}\left( {1 - {\varepsilon _k}} \right) \approx \\ 1 - {\left[ {\int_0^{g_k^{{\rm{th}}}} {{f_g}} (x){d_x}} \right]^{{N_k}}} - {\varepsilon _k} \end{array} $ | (7) |
其中,εk和
| $ \operatorname{Pr}\left\{l_{k}=1\right\} \approx 1-f_{u}\left(r_{k}, N_{k}, B_{k}, \varepsilon_{k}\right) $ | (8) |
从而满足上行链路的可靠性可表示为fu(rk, Nk, Bk, εk)≤εmax .
3 无线资源优化方案在确保总带宽达到了迟延和可靠性的性能前提下,通过优化子信道的数量(Nk,k=1, 2, …, Ka)、每个子信道的带宽(Bk, k=1, 2, …, Ka)和每个用户的信道增益的门限值来最小化系统所需的总带宽
| $ \mathop {\min }\limits_{{N_k}, {B_k}, {\varepsilon _k}\atop k = 1, \cdots , {K_a}} \sum\limits_{k = 1}^{{K_a}} {{N_k}} {B_k} $ | (9) |
| $ {\rm s.t.}~~ 0<B_{k} \leqslant W_{c} $ | (9a) |
| $ 0<N_{k} \leqslant N_{\max } $ | (9b) |
| $ 0<\varepsilon_{k} \leqslant \varepsilon_{\max } $ | (9c) |
| $ 0<D_{k} \leqslant D_{\max } $ | (9d) |
| $ f_{u}\left(r_{k}, N_{k}, B_{k}, \varepsilon_{k}\right) \leqslant \varepsilon_{\max } $ | (9e) |
其中:Ka表示用户设备在一帧内传输的数据包数,设置每个帧的持续时间Tf=0.1 ms.
由于每个用户的约束条件不受其他用户影响,式(9)中的问题可以等价的分解为单用户设备问题,即
| $ \min\limits_{N_{k}, B_{k}, \varepsilon_{k}} N_{k} B_{k} $ | (10) |
s.t. (9a)(9b)(9c)(9d)(9e)
为了解决该优化问题,根据文献[11]给出定理,可以对基于距离的可靠性函数fu(rk, Nk, Bk, εk)进行分析,由于篇幅原因,详细证明过程省略.
定理1 给定Nk、εk、rk,fu(rk, Nk, Bk, εk)在Bk上是递减的.
定理2 给定Nk、rk,fu(rk, Nk, Bk, εk*(Bk))随着Bk的增加而减少,εk*(Bk)是使得fu(rk, Nk, Bk, εk*(Bk))最小的最优值.
定理3 给定Nk、Bk、rk,当gkth < Nt-1时,fu(rk, Nk, Bk, εk)在εk上是凸的.
根据定理2和3,给定Nk、rk,可以得到最优的Bk、εk,从而得到满足式(11)的最优解{Nk*,Bk*,εk*},考虑到εk的求解区间很小,采用精确线性搜索方法求最优解较为合理,因此提出一种基于黄金分割法的εopt搜索算法来求解优化问题,具体过程见算法1.
算法1 基于黄金分割的εopt搜索算法
步骤1 确定初始搜索区间(a0, b0)和算法精度ξ,令
步骤2 若fu(rk, Nk, Bi, εi)≤fu(rk, Nk, Bi*, εi*),转步骤3,否则转步骤4.
步骤3 计算左分割点.若|εi*-ai|≤ξ,令εopt=εi,转步骤5;否则,令ai+1=ai, bi+1=εi*, fu(rk, Nk, Bi+1*, εi+1*)=fu(rk, Nk, Bi, εi), εi+1*=εi, εi+1=ai+1+(1-t)(bi+1-ai+1).计算fu(rk, Nk, Bi+1, εi+1), i=i+1,转步骤2.
步骤4 计算右分割点.若|bi-εi|≤ξ,令εopt=εi*,转步骤5;否则,令ai+1=εi, bi+1=bi, fu(rk, Nk, Bi+1*, εi+1*)=fu(rk, Nk, Bi, εi), εi+1=εi*, εi+1*=ai+1+t(bi+1-ai+1).计算fu(rk, Nk, Bi+1*, εi+1*), i=i+1,转步骤2.
步骤5 输出最优解εopt,fu(rk, Nk, Bopt, εopt).
该算法中,搜索区间的搜索率t≈0.618,该算法每次迭代只需计算1次fu(rk, Nk, Bk, εk)的值.
为了得到式(9)中的最优解,可以将式(11)中的优化问题进行Ka次求解.具体的过程见算法2.
算法2 最小化系统所需的总带宽算法
步骤1 输入Nk、rk,当Nk≤Nmax 时,初始值
步骤2 若fu(rk, Nk, Bopt, εopt)>εmax,转步骤1,更新初始值
步骤3 若fu(rk, Nk, Bopt, εopt) < εmax,Bk(Nk)=Bopt,εk(Nk)=εopt或者Bk(Nk)=NaN,εk(Nk)=NaN.
步骤4 求出
步骤5 重复步骤1-4Ka次,输出最优解{Nk*,Bk*,εk*}.
4 仿真分析利用Matlab软件仿真验证所提出算法的性能,并与文献[10-11]进行比较.系统包括一个蜂窝基站、MTC用户数为K=1 000,用户设备在离基站[50, 250]之间均匀分布,路径损耗模型为-10lg (μk)=35.3+37.6lg (rk),用户设备的最大发射功率Pmax=23 dBm,基站所需的平均接收功率ρ0=-40 dBm,路径损耗指数α=3,包长20 byte,N0=-174 dBm/Hz,Wc=0.5 MHz,Tf=0.1 ms,给用户设备分配的最大子信道数Nmax=10.
4.1 不同参数对信道分配的影响分析仿真分析不同参数(重点是距离、天线数、用户数、可靠性等)对信道分配(子信道、带宽)的影响.在不同的MTC设备应用场景中,对QoS需求中可靠性要求可能不相同,因此,图 1给出了εmax =10-6和εmax =10-7时(需要说明的是,若加上信道编码的纠错功能,可靠性或丢包率可以达到10-8~10-9,能够满足实际应用需求)每个用户在离基站不同距离下分配的子信道的最优数.如果基站只有2根天线,即使当Bk=Wc,Nk=Nmax,在小区的边缘一些用户的QoS需求也得不到满足,不能解决式(9)中的优化问题;当Nt≥16时,用户分配得到的子信道数为1,也就是说,当基站的天线数量相对较大时,频率多样性就显得不太重要.从图 1(a)(b)对比得出,当对可靠性的要求提高时,用户分配到的子信道数会有所增加,这是因为系统的QoS性能提高时,对传输信道质量要求更高.
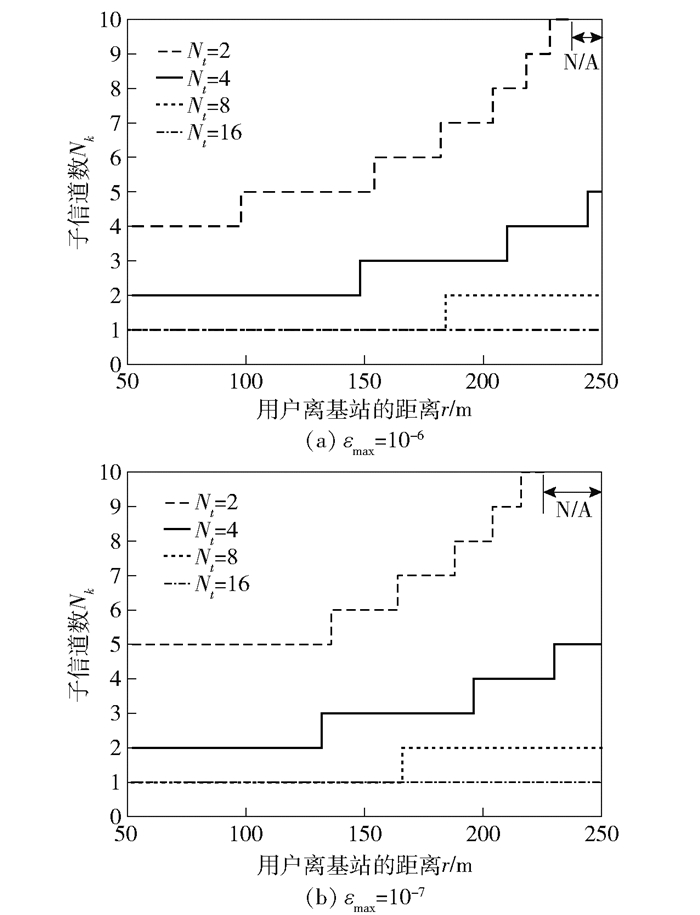
|
图 1 距离和子信道数关系 |
图 2给出了系统需要的总带宽与天线数的关系曲线,仿真参数设置为:Ka=1 000,Nt=8,Nt=16和Nt=32,εmax=10-7,与文献[11]中发射功率为最大发射功率不同的是本文方案的发射功率采用反向功率控制机制.从图 4中可以看出,随着天线数的增加,系统所需带宽随之减少,当天线数为32时,所需要的带宽大约为155 MHz;而当天线数为8时,所需要的带宽大约为286 MHz.这是因为随着天线数的增加,增加了空域的多样性,用户分配得到的子信道数会减少,这使得系统占用的总带宽减少.对比文献[11]中的最大功率发射方案,两者在相同天线数下,所需的带宽相差不大,2种方案中所需的总带宽曲线基本重合,在总带宽性能方面差异不是很明显.
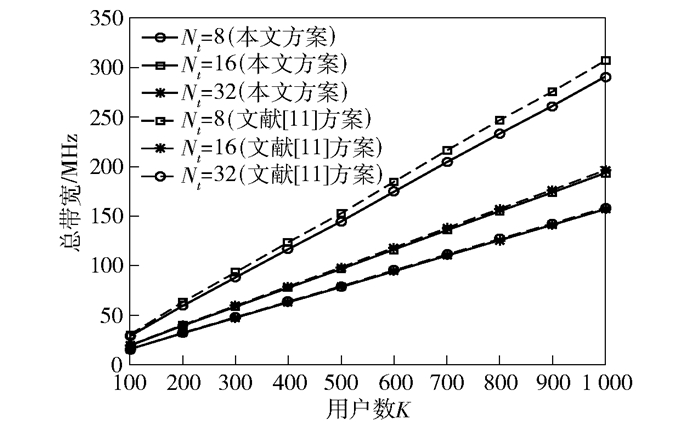
|
图 2 用户数与总带宽关系曲线 |
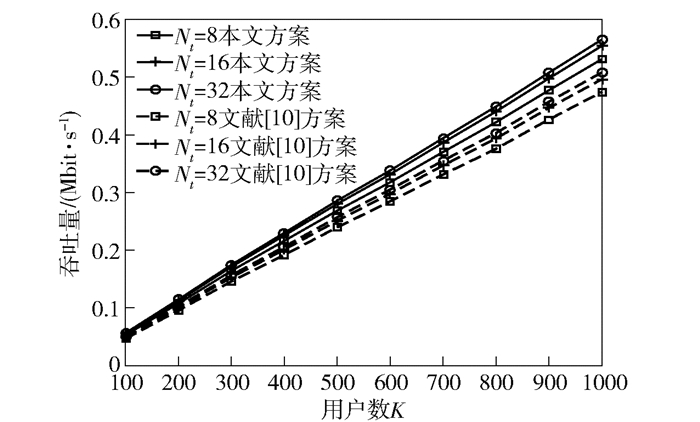
|
图 4 用户数与吞吐量关系曲线 |
以下重点仿真分析用户数对功耗、吞吐量和能量效率等性能的影响.从图 3的用户数与总功率的关系曲线可以看出,对发射功率进行了控制,系统所需的功率比文献[11]中所提的最大功率发送要小很多,这是因为在距离基站较近的地方,当ρ0rkα < Pmax时,用户不以最大功率发送,用户的发射功率为ρ0rkα,只有在离基站很远的地方,当ρ0rkα≥Pmax时,发射功率为Pmax,考虑了距离因素后,该功率控制方案的效果将更好.由图 2可知,仿真结果证明了所需总带宽基本差不多,但是在功率方面,笔者所采用的方案比文献[11]中的方案更具有性能优势.
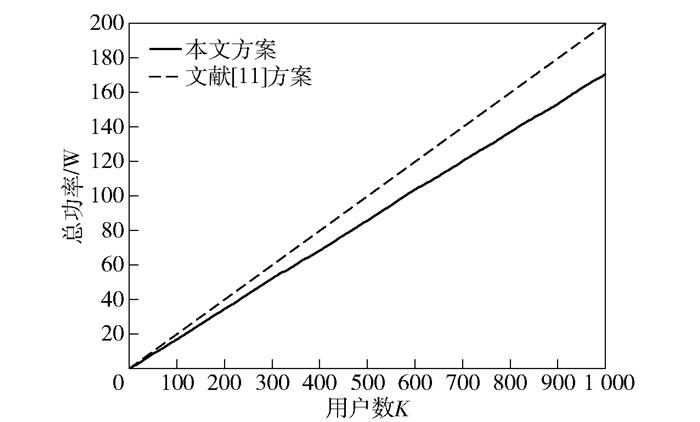
|
图 3 用户数与总功率关系曲线 |
图 4所示为不同功率分配算法方案下系统吞吐量随用户数变化的关系曲线,由图可知,当天线数增加时,2个方案下的总吞吐量都会增加,这是因为当天线数增加时,增加了空域的多样性,从而增加了总吞吐量;另外,与文献[10]中所提的功率分配算法方案相比较,本文方案的吞吐量性能明显优于文献[10]方案,这得益本文信道反向功率控制算法的有效性,因此得到的吞吐量性能比文献[10]方案中的吞吐量性能好.
图 5所示为不同功率分配算法方案下能量有效性随用户数变化的关系曲线.能量有效性定义为系统的吞吐量与总功率之间的比值,为了降低传输功率提高能量效率,在上行链路进行反向功率控制.由图可知,当天线数增加时,系统的吞吐量会增大,而用户的发射功率与天线数无关,所以天线数多的能量有效性性能比同方案下天线数少的性能要好.另外,与文献[10]中所提的功率分配算法方案相比较,本文方案的能量有效性性能明显优于文献[10]中的方案,这是因为文献[10]的功率分配不够有效,导致在同样带宽资源传输功率较高,吞吐量反而较低.
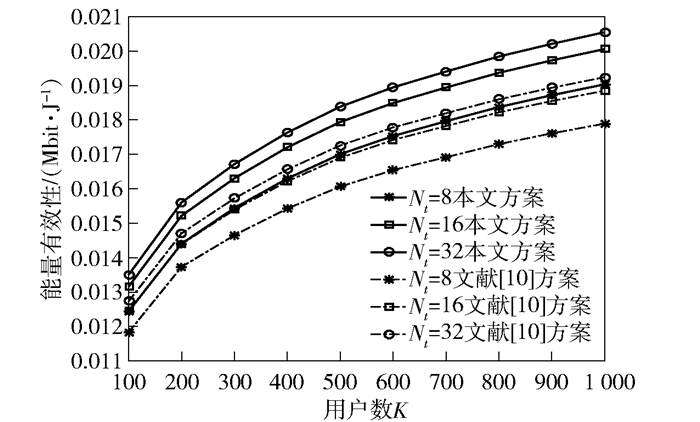
|
图 5 用户数与能量有效性关系曲线 |
研究了mMTC中TDD上行传输的无线资源优化,提出了一种mMTC中基于功率控制的高可靠低迟延上行无线资源管理方案.为了满足系统的QoS需求,没有采用重传机制.考虑一个基于可实现速率的传输模型,设计上行链路传输的反向功率控制方案,分析了链路可靠性函数的特性,建立了上行无线资源优化公式,并提出了一种基于黄金分割的搜索最优的传输错误概率算法以及一种最小化系统所需的总带宽算法,为每个用户分配多个子信道,从而优化系统所需的总带宽.仿真结果显示,与对比方案相比,本文方案和算法在迟延和可靠性的改进以及在功耗、能量效率、总带宽、吞吐量等性能具有优势.下一步,将考虑点对点通信和中继传输的高可靠低迟延资源分配.
| [1] |
Soltanmohammadi E, Ghavami K, Naraghi-Pour M. A survey of traffic issues in machine-to-machine communications over LTE[J]. IEEE Internet of Things Journal, 2016, 3(6): 865-884. DOI:10.1109/JIOT.2016.2533541 |
| [2] |
Alberto Rico-Alvari, Madhavan Vajapeyam, Hao Xu, et al. An overview of 3GPP enhancements on machine to machine communications[J]. IEEE Communications Magazine, 2016, 54(6): 14-21. DOI:10.1109/MCOM.2016.7497761 |
| [3] |
Osseiran A, Boccardi F, Braun V, et al. Scenarios for 5G mobile and wireless communications:the vision of the METIS project[J]. IEEE Communications Magazine, 2014, 52(5): 26-35. DOI:10.1109/MCOM.2014.6815890 |
| [4] |
Meryem Simsek, Adnan Aijaz, Mischa Dohler, et al. 5G-enabled tactile internet[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(3): 460-473. DOI:10.1109/JSAC.2016.2525398 |
| [5] |
3GPP R1-120056, Analysis on traffic model and characteristics for MTC and text proposal[S]. TSG-RAN Meeting WG1#68, Dresden: [s.n.], 2012.
|
| [6] |
Aijaz A. Towards 5G-enabled tactile internet: radio resource allocation for haptic communications[C]//IEEE Wireless Communications and Networking Conference (WCNC). 2016: 145-150. https://ieeexplore.ieee.org/document/7564661
|
| [7] |
Chen J J, Liang J M, Chen Z Y. Energy-efficient uplink radio resource management in LTE-advanced relay networks for internet of things[C]//IEEE Wireless Communications and Mobile Computing Conference (IWCMC). 2014: 745-750. https://ieeexplore.ieee.org/document/6906449
|
| [8] |
Aijaz A, Aghvami A H. On radio resource allocation in LTE networks with machine-to-machine communications[C]//IEEE 77th Vehicular Technology Conference (VTC Spring). 2013: 1-5. https://ieeexplore.ieee.org/document/6692664
|
| [9] |
Aijaz A, Tshangini M, Nakhai M R, et al. Energy-efficient uplink resource allocation in LTE networks with M2M/H2H co-existence under statistical QoS guarantees[J]. Communications IEEE Transactions on, 2014, 62(7): 2353-2365. DOI:10.1109/TCOMM.2014.2328338 |
| [10] |
She C, Yang C, Quek T Q S. Cross-layer optimization for ultra-reliable and low-latency radio access networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(1): 127-141. DOI:10.1109/TWC.2017.2762684 |
| [11] |
She C, Yang C, Quek T Q S. Uplink transmission design with massive machine type devices in tactile internet[C]//Proceeding of IEEE Globecom Workshops.[s.l.]: IEEE, 2016: 1-6. https://ieeexplore.ieee.org/document/7849072
|
| [12] |
Yang W, Durisi G, Koch T, et al. Quasi-static multiple-antenna fading channels at finite blocklength[J]. IEEE Transactions on Information Theory, 2013, 60(7): 4232-4265. |
| [13] |
Liu L, Yi Y, C. J. -F, et al. Energy-efficient power allocation for delay-sensitive multimedia traffic over wireless systems[J]. Vehicular Technology, 2014, 63(5): 2038-2047. DOI:10.1109/TVT.2014.2313864 |
| [14] |
Chen S, Sun S, Wang Y, et al. A comprehensive survey of TDD-based mobile communication systems from TD-SCDMA 3G to TD-LTE(A) 4G and 5G directions[J]. China Communications, 2015, 12(2): 40-60. DOI:10.1109/CC.2015.7084401 |


