能量检测算法应用于无线通信场景中时存在信噪比(SNR)墙和噪声不确定性问题,对此,在认知无线电非同分布高斯信号背景下,提出了基于增强能量检测的协作感知算法.在低SNR条件下,给出了采用增强能量检测算法的次用户检测概率和虚警概率,并推导出达到最小总错误率的最优协作用户数表达式.理论分析和仿真实验结果表明,相对其他克服噪声不确定性的能量检测算法,所提出的算法具有更优的检测性能.
In wireless communication scenarios, energy detection has disadvantage in signal-to-noise ratio (SNR) wall and noise uncertainty. The article presents enhanced energy detection with cooperative spectrum sensing under non-identical Gaussian background noise in cognitive radio. Furthermore, the probability of detection and the probability of false alarm have been derived for enhanced energy detection under low SNR condition in cooperative spectrum sensing, and the number of optimized collaboration users has been deduced for the minimum total error rate. Theoretical analysis and numerical results show that proposed schemes have better detection performance than other energy detection plans for solving noise uncertainty problem.
随着无线通信技术的发展,认知无线电技术能提高频谱资源的利用率,广泛应用于物联网,而频谱感知技术的开发更进一步推广了基于认知无线电的物联网发展与应用[1-2].非相关信号检测技术——能量检测具有低复杂性和检测无需先验信号等优点[1-4],广泛应用于认知无线电和超宽带系统中,以解决无线通信中频带稀缺的问题.由于能量检测算法的单门限变化会产生噪声不确定性的问题,且当信噪比(SNR, signal-to-noise ratio)低于一定阈值时,能量检测算法几乎完全失效(能量检测的SNR墙的缺点)[3].因此,如何在实际的通信场景中克服能量检测算法的噪声不确定性和SNR墙缺点是当前信号检测待解决的关键问题.
针对这2个问题,Farag等[3]提出了考虑噪声不确定性的双门限能量检测算法,但变化的双门限无法保证算法在低虚警概率条件下达到高检测概率. Yu等[5]研究了动态门限的能量检测,以提高在低SNR条件下的信号检测概率,但是噪声的微小变化会大幅改变算法的门限,从而导致算法的检测性能产生巨大改变. Martínez等[6]研究了在低SNR条件下的能量检测问题,提出了基于协方差矩阵的特征值化简算法,但当此算法的检测概率接近1时,虚警概率也接近1,因而算法在检测概率要求很高的场景中失效.综上所述,如何在低SNR场景中克服能量检测算法的噪声不确定性问题,并保证算法具有高检测概率和低虚警概率且复杂度适中,是一个待解决的关键问题.
笔者提出了2种增强的能量检测算法,第1种采用2次自适应门限判决,第2种采用1次凸优化门限判决,前者相对后者具有更优的检测概率但是复杂度相对较高.所提算法能在非同分布高斯信号背景下,解决低SNR条件下的检测最优化问题,达到最小总错误率.仿真实验结果表明,所提算法和其他能量检测算法相比具有更低的总错误率.
1 系统模型未知随机信号的检测定义为二元假设检验[6]:
| $ H_{0} : y(t)=n(t) \\ H_{1} : y(t) =h s(t)+n(t) $ | (1) |
其中:H0表示信号存在,H1表示信号不存在,y(t)为次用户接收端接收信号,h为无线信道增益,s(t)为待检测主用户信号且其噪声为σs2,n(t)为噪声是σc2的加性白高斯噪声.传统的能量检测算法表示为
| $ Y = \frac{1}{k}\sum\limits_{i = 1}^k {\frac{{{y^2}(i)}}{{\sigma _c^2}}} $ | (2) |
其中:k为接收信号分量的计算样本数,Y为接收端计算的总信号能量.假设能量检测的门限定义为λ,如果Y≥λ,则判定信号存在,否则判定信号不存在. y(t)的概率密度函数(p, d, f)表示为[7]
| $ \begin{array}{l} {f_Y}(y) = \\ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{2^{\frac{k}{2}}}\mathit{\Gamma }(k)}}{y^{\frac{k}{2} - 1}}{{\rm{e}}^{ - \frac{x}{2}}}, \quad {H_0}}\\ {\frac{1}{2}{{\left( {\frac{y}{{2\gamma }}} \right)}^{\frac{k}{4} - \frac{1}{2}}}{{\rm{e}}^{ - \frac{y}{2} - \gamma }}{{\rm{I}}_{\frac{k}{2} - 1}}(\sqrt {2y\gamma } ), \quad {H_1}} \end{array}} \right\} \end{array} $ | (3) |
其中:γ表示信噪比,Iu-1表示阶数为u-1的第一类修正贝塞尔函数,Г(·)表示Gamma函数,Г(·, ·)表示不完全Gamma函数.检测概率Pd和虚警概率Pf表示为[7]
| $ P_{d}=P_{r}\left(y>\lambda | H_{1}\right)=Q_{u}(\sqrt{2 \gamma}, \sqrt{\lambda}) $ | (4) |
| $ P_{f}=P_{r}\left(y>\lambda | H_{0}\right)=\frac{\Gamma\left(u, \frac{\lambda}{2}\right)}{\Gamma(u)} $ | (5) |
其中:Pr(·)表示概率分布函数,u为时间带宽积,Qu(a, b)表示u阶广义Marcum-Q函数.
在协作感知场景中,每个次用户同时对融合中心发送对主用户状态的二元判断Di(Di=1或者0,1代表H1,0代表H0),融合中心将收到的总数据和设定整数v相比,判决如下:
| $ \sum\limits_{i = 1}^M {{D_i}} \left\{ {\begin{array}{*{20}{l}} { \ge v, }&{{H_1}}\\ { < v, }&{{H_0}} \end{array}} \right. $ | (6) |
其中正整数M为次用户数.当v=1时,式(6)表示“或”协作方式;当v=M时,式(6)表示“和”协作方式.
2 增强的能量检测算法 2.1 两次自适应判决γ和γ′基于增强能量检测的协作感知框架如图 1所示,假设在协作感知中有m(1≤q≤m)个独立的认知用户分别进行信号检测,此时协作感知的二元假设检验问题表示为

|
图 1 高斯信号噪声不确定性背景下基于增强能量检测的协作感知框架 |
| $ \left. \begin{array}{l} {H_0}:{y_{q\tau }}(t) = {n_{q\tau }}(t)\\ {H_1}:{y_{q\tau }}(t) = h{s_\tau }(t) + {n_{q\tau }}(t) \end{array} \right\} $ | (7) |
类似于式(1),其中τ表示能量检测信号第τ(τ=1, 2, …, k)个分量数,yqτ(t)表示第q个次用户的第τ个接收信号,nqτ(t)表示第q个次用户的第τ个噪声分量且方差为σc2,h表示无线信道增益,sτ(t)表示噪声为στ2的接收信号.
假设每个次用户都有独立的能量检测器,结合实际化简的高斯信号噪声值,根据接收噪声设定增强能量检测算法的动态门限最小值和最大值(最小值和最大值分别定义为γmin和γmax,其中1≤q≤m)
| $ \left. {\begin{array}{*{20}{l}} {{\gamma _{\min }} = \min \sum\limits_{\tau = 1}^k {\frac{{y_{m\tau }^2}}{{\sum\limits_{\tau = 1}^k {\frac{{\sigma _{m\tau }^4}}{{\sigma _{q\tau }^2}}} }}} }\\ {{\gamma _{\max }} = \max \sum\limits_{\tau = 1}^k {\frac{{y_{m\tau }^2}}{{\sigma _{q\tau }^2}}} } \end{array}} \right\} $ | (8) |
根据式(8),若实际的能量接收值大于γmax,则判定H1;否则,若实际的能量接收值小于γmin,则判定H0.这里采用分段判决法对动态门限进行判决,能降低算法的复杂度.当实际接收能量值介于[γmin, γmax]之间时,进行再次判决,门限值γ′定义为
| $ {\gamma ^\prime } = \sum\limits_{\tau = 1}^k {\frac{{y_{m\tau }^2}}{{\sum\limits_{\tau = 1}^k {\frac{{\sigma _{m\tau }^4}}{{E\left( {\sigma _{m\tau }^2} \right)}}} }}} $ | (9) |
不同于2.1节考虑多噪声不确定性的两次自适应判决,从低复杂度的角度考虑,提出一次凸优化判决算法γ″(提出算法的复杂度在第3节讨论).此时,根据第3节化简得到的多高斯信号噪声动态调整判决门限γ″,其表示为(由于要求更优的检测概率,故设定更低的门限[8])
| $ {\gamma ^{\prime \prime }} = \sum\limits_{\tau = 1}^k {\frac{{y_{m\tau }^2}}{{\sum\limits_{\tau = 1}^k {\frac{{\sigma _{m\tau }^4}}{{\min \frac{{\sum\limits_{i = 1, 1 \le e \le \tau }^\tau {{\mu _i}} E\left( {\sigma _{me}^2} \right)}}{{\sum\limits_{\tau = 1}^\tau {{\mu _i}} }}}}} }}} $ | (10) |
其中μi=σme2 /σm(τ-e)2,且σme2(1≤e≤τ)从小到大进行排列.值得注意的是,当μτ-i=1时,式(10)的凸优化判决门限将化简为式(9).
3 非同分布高斯信号噪声背景下的化简假设图 1中的非同分布高斯信号定义为xi~N(μi, σi2),根据文献[6, 9],定义信号向量矩阵X=[x1, x2, …, xk]及其厄米特共轭矩阵XH=[x1, x2, , xk]H,则协方差矩阵表示为
| $ \mathit{\boldsymbol{N}} = \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{H}}} $ | (11) |
将高斯信号期望化简为0,得到
| $ E\left( {\sigma _{i\mu }^2} \right) = E\left( {{x_{im}}x_{i\mu }^{\rm{H}}} \right) - E\left( {{x_{i\mu }}} \right)E\left( {x_{i\mu }^{\rm{H}}} \right) $ | (12) |
化简式(11)中向量矩阵,有
| $ \begin{array}{c} E\left( {\sigma _{\tau k}^2} \right) = {\mathop{\rm Var}\nolimits} \left( {\sum\limits_{i = 1}^k {\frac{{(\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{U}}){{(\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{U}})}^{\rm{H}}}}}{{\sigma _i^2}}} } \right) = \\ {\mathop{\rm Var}\nolimits} \left( {\sum\limits_{i = 1}^k {\frac{{\sum\limits_{\tau = 1}^k E \left( {{x_{tk}}x_{\tau k}^{\rm{H}} - {x_{\tau k}}u_{\tau k}^{\rm{H}} - {u_{\tau k}}x_{\tau k}^{\rm{H}} + {u_{\tau k}}u_{\tau k}^{\rm{H}}} \right)}}{{\sigma _i^2}}} } \right) \end{array} $ | (13) |
其中:Var(·)表示方差,uτkH~N(μτk, 0),U=[u1, u2, …, uk],UH=[u1, u2, …, uk]H.对式(13)中的矩阵噪声做列均值化(可达到减小噪声间方差的目的,并降低代入式(8)~式(10)之后的复杂度):
| $ E\left(\sigma_{\tau}^{2}\right)=\frac{1}{k} \operatorname{Var}\left(\sum\limits_{i=1}^{k} \frac{\boldsymbol{X} \boldsymbol{X}^{\mathrm{H}}+\boldsymbol{U} \boldsymbol{U}^{\mathrm{H}}}{\sigma_{i}^{2}}\right) $ | (14) |
进一步地,假设在不同时刻采用能量检测算法对高斯信号(正态分布)进行离散抽样,且抽样值汇聚于正态分布的中间区域且置信度为1-α,则化简后的置信区间满足
| $ \begin{array}{c}\left\{\mu_{i} | \sigma_{k}^{2}\right\} \subset &\left[\overline{\mu}-z_{\frac{\alpha}{2}} \frac{\sigma_{k}}{2}, \overline{\mu}+z_{\frac{\alpha}{2}} \frac{\sigma_{k}}{\sqrt{k}}\right], \\ z_{\frac{\alpha}{2}}=\frac{\overline{\mu}-E\left(\mu_{i}\right)}{\sqrt{\sigma_{k}^{2} / k}} & \end{array} $ | (15) |
其中:
| $ \left\{ {{\mu _i}|\sigma _k^2} \right\} \subset \left[ {\left( {\bar \mu - {z_{\frac{{0.01}}{2}}}{\sigma _k}} \right)\frac{{{z_{\frac{{0.2}}{2}}}}}{{{z_{\frac{{0.01}}{2}}}}}, \left( {\bar \mu + {z_{\frac{{0.01}}{2}}}{\sigma _k}} \right)\frac{{{z_{\frac{{0.2}}{2}}}}}{{{z_{\frac{{0.01}}{2}}}}}} \right] $ | (16) |
由式(2)、式(8)~式(10)、式(14)和式(16)可知,传统的能量检测算法复杂度为m(τ-1),提出的两次自适应判决算法复杂度为α1m(τ-1)2+α2m(τ-1)2+O(mτ)(其中α1和α2表示和为1的2个正常数),提出的一次凸优化判决算法复杂度为m(τ-1)2+O(mτ2).因此,与传统能量检测算法相比,提出算法并没有显著增大复杂度.
4 融合中心总错误率最优化在图 1中,当增强的能量检测算法在非同分布高斯信号背景下经过噪声化简后,根据式(8)~式(10)动态调整增强能量检测算法的判决,并根据式(1)和式(2),基于二元假设检验的能量检测算法的虚警概率和误检概率分布函数表示为[10]
| $ P_{f, \tau}=P_{r}\left(H_{1} | H_{0}\right)=1-\int_{0}^{\gamma} f_{y | H_{0}}(y) \mathrm{d} y $ | (17) |
| $ P_{m, \tau}=P_{r}\left(H_{0} | H_{1}\right)=1-\int_{0}^{\gamma} f_{y | H_{1}}(y) \mathrm{d} y $ | (18) |
其中:Pr(·)表示概率分布函数,f(·)表示概率密度函数.根据文献[10]中的式(6),结合式(8)~式(10),采用数学归纳法推导采用增强能量检测算法的独立次用户虚警概率函数为
| $ {P_r}\left( {\frac{{y_i^2}}{{{{\left( {{w^{\frac{1}{2}}}} \right)}^p}}} \le y} \right) = \frac{2}{p}{y^{\frac{2}{p} - 1}}{f_{\frac{{y_i ^2}}{{\left( {w\frac{1}{2}} \right)p}}}}\left( {{y^{\frac{2}{p}}}} \right) $ | (19) |
其中w为噪声期望值.结合式(9),当p=2时,虚警概率的分布函数和概率密度函数为
| $ {P_r}\left( {\frac{{y_i^2}}{w} \le y} \right) = {f_{\frac{{y_i^2}}{w}}}(y) $ | (20) |
| $ f_{w | H_{0}}(y)=\frac{\partial P_{r}\left(\frac{y_{i}^{2}}{w} \leqslant y\right)}{\partial y}=\frac{\exp \left(-\frac{y}{w}\right)}{w} $ | (21) |
类似于式(19)~式(21),采用数学归纳法,检测概率的概率密度函数为
| $ f_{w | H_{1}}(y)=\frac{\exp \left(-\frac{y}{w(1+\overline{\gamma})}\right)}{w(1+\overline{\gamma})} $ | (22) |
其中γ为平均SNR.
当协作用户数为m时,采用“或”判决的单个次用户的误检概率、协作感知的虚警概率和误检概率分别表示为[10]
| $ P_{m}=1-P_{d} $ | (23) |
| $ Q_{f}=1-\left(1-P_{f}\right)^{m} $ | (24) |
| $ Q_{m}=\left(1-P_{d}\right)^{m} $ | (25) |
其中:Pm为单个次用户的误检概率,Qf为协作感知的虚警概率,Qm为协作感知的误检概率.由文献[8]得到总错误率的表达式为
| $ Q_{e}=P_{r}\left(H_{0}\right) Q_{f}+P_{r}\left(H_{1}\right) Q_{m} $ | (26) |
其中:Pr(H0)为关于假设检验H0的常数,Pr(H1)为关于假设检验H1的常数且Pr(H0)+Pr(H1)=1.在式(26)中假设Pr(H0)=α,结合式(8)~式(10)和式(16),在非同分布高斯信号的多噪声条件下的总错误率为
| $ \begin{array}{*{20}{c}} {{Q_e} = \sum\limits_{\sigma _t^2} {{P_r}} \left( {{H_0}} \right){P_r}\left( {\sigma _i^2|{H_0}} \right){Q_f} + }\\ {{P_r}\left( {{H_1}} \right){P_r}\left( {\sigma _i^2|{H_1}} \right){Q_m}} \end{array} $ | (27) |
进一步地,在信号判决状态条件下结合多噪声推导总错误率得到
| $ \begin{array}{c} Q_e^\prime = \sum\limits_{\sigma _i^2( \cdot ), {P_r}\left( {{H_0}, \sigma _i^2\left( {{Q_f}} \right)} \right){Q_f} = {P_r}\left( {{H_1}, \sigma _i^2\left( {{Q_m}} \right)} \right){Q_m}} {{P_r}} \left( {{H_0}} \right) \times \\ {P_r}\left( {\sigma _i^2\left( {{Q_f}} \right)|{H_0}} \right){Q_f} + {P_r}\left( {{H_1}} \right){P_r}\left( {\sigma _i^2\left( {{Q_m}} \right)|{H_1}} \right){Q_m} \end{array} $ | (28) |
对式(28)中在信号判决条件的限制Pr(H0, σi2(Qf))Qf=Pr(H0, σi2(Qm))Qm下,当噪声数大于2时,σi2(·)一定有解.另一方面,将式(17)~式(27)代入式(28),类似于文献[8]求解达到最小总错误率的最小协作用户数M*,结合式(26),最小协作用户数的求解表示为
| $ \begin{array}{*{20}{c}} {{M^*} = \arg \mathop {\min}\limits_M \left( {\alpha \frac{{\partial {Q_f}}}{{\partial M}} + (1 - \alpha )\frac{{\partial {Q_m}}}{{\partial M}}} \right) = }\\ {\quad \arg \mathop {\min}\limits_M \left( {\alpha \frac{{\partial {Q_f}}}{{\partial M}} - (1 - \alpha )\frac{{\partial {Q_d}}}{{\partial M}}} \right)} \end{array} $ | (29) |
由于式(29)中Qf(u, M, σi2)和Qd(u, γ, M, σi2)的自变量不完全相同,对式(29)进一步求解最小协作用户数:
| $ \begin{array}{C} {M^*} = \left\lceil {\mathop {\arg }\limits_M \frac{{\min \alpha \frac{{\partial {Q_f}}}{{\partial M}}}}{{\max (1 - \alpha )\frac{{\partial {Q_d}}}{{\partial M}}}}} \right\rceil = \\ \left\lceil {\arg \mathop {\min }\limits_M \frac{{\alpha \frac{{\partial {Q_f}}}{{\partial M}}}}{{(1 - \alpha )\frac{{\partial {Q_d}}}{{\partial M}}}}} \right\rceil \end{array} $ | (30) |
其中⌈·⌉表示取上整函数.
5 仿真实验结果所提算法解决能量检测算法在非同分布高斯信号背景下的噪声不确定性问题和SNR墙问题,因此与应用于不同场景中解决噪声不确定问题和SNR墙问题的其他能量检测算法进行对比[7-13].由于提出算法主要针对高检测要求的场景,所以从误检概率、低SNR条件下的最优检测以及最小协作用户数条件下的最优检测3个方面进行提出算法性能对比分析.由文献[8]的图 2得到传统的能量检测算法在协作场景中最优检测门限λ=30,最优协作用户数M*=5;由文献[10]得到应用于非完美信道的低SNR能量检测错误率q=0.001,应用于多跳场景中在低SNR条件下的检测跳数为10,类似于文献[13]假设噪声σmτ2在区间[0, 2]范围内变化且采用式(2)、式(8)~式(10)进行能量检测值的抽样计算,另一方面,在式(15)中的置信度假设为α=0.2,式(21)和式(22)中w=E(σmτ2).
|
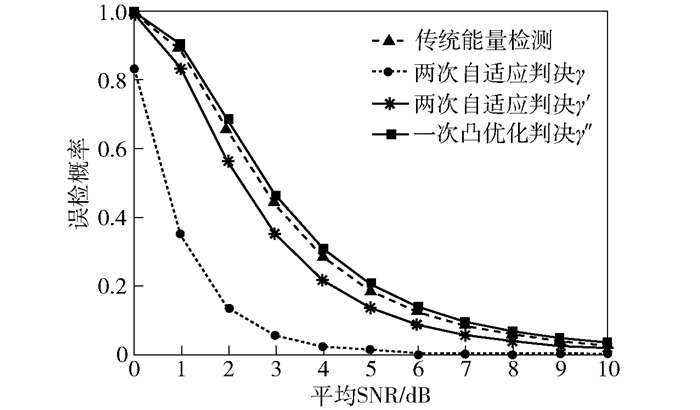
图 2 误检概率和平均SNR的关系 |
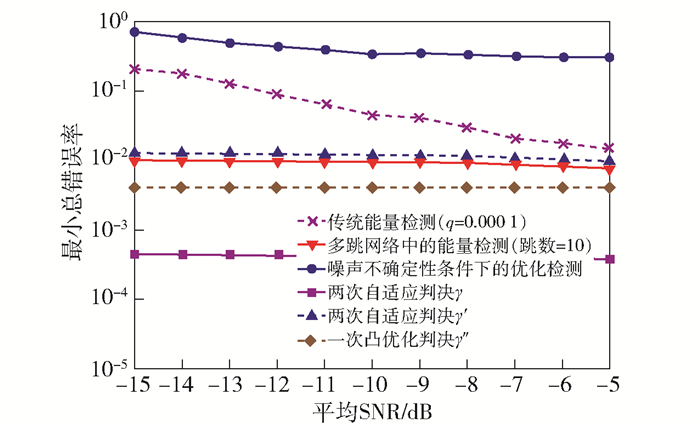
图 2所示为提出算法与传统的能量检测算法在平均SNR增大的条件下,误检概率的变化. 图 3所示为增强的能量检测算法和传统的能量检测算法在平均SNR很低且变化的条件下,最小总错误率的变化[11-13]. 图 2和图 3都采用式(27)的计算模型,并在融合中心采用“或”模型的硬判决.
|
图 3 最小总错误率和平均SNR的关系 |
图 2和图 3表明,随着平均SNR的升高,提出算法相对传统算法具有更优的误检概率和更小的总错误率,能在低SNR条件下更好地克服噪声不确定的缺点.尽管两次自适应判决算法具有更低的误检概率和更小的总错误率,但其需要两次判决,因而复杂度相对较高;而一次凸优化判决算法的检测性能虽然比不上两次自适应判决算法,但其仅需要一次判决,因而复杂度相对较低.
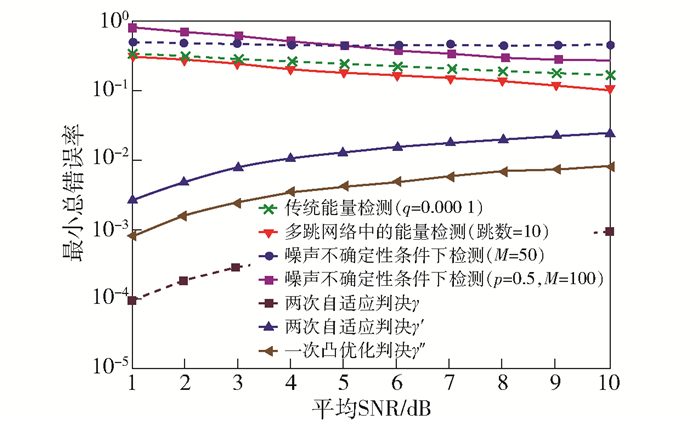
另一方面,假设在-10 dB的低SNR条件下,对比分析最小总错误率和平均SNR的关系. 图 4表明,随着最小协作用户数的增加,尽管提出算法的最小总错误率在一定程度上会增大(因为在低SNR条件下,随着协作用户数的增加,误检概率的降低小于虚警概率的升高,因此二者之和使最小总错误率升高),但总的来说,提出算法在有效克服多噪声不确定性的同时,相对其他算法能达到更低的最小总错误率,且与文献[10]中的认知无线区域网络标准下的最小总错误率0.1相比,提出算法的最小总错误率远低于这个值.由此可见,提出算法与其他算法相比,不但能在低SNR条件下更有效地进行信号检测,还能更好地解决能量检测的噪声不确定性问题.
|
图 4 最小总错误率和最优协作用户数的关系 |
笔者提出了非同分布高斯信号背景下基于增强能量检测的协作感知算法,以解决传统的能量检测算法在检测中出现的SNR墙和噪声不确定性问题.提出算法能在低SNR条件下达到更小的总错误率,有效克服了高斯信号的噪声不确定性缺点,且复杂度相对适中.仿真实验结果表明,与其他场景中的能量检测算法相比,提出算法不但在低SNR条件下具有更优的检测性能,还能更好地解决能量检测算法的噪声不确定性问题.
| [1] |
Khan A A, Rehmani M H, Rachedi A. Cognitive-radio-based internet of things:applications, architectures, spectrum related functionalities, and future research directions[J]. IEEE Wireless Communications, 2017, 24(3): 17-25. DOI:10.1109/MWC.2017.1600404 |
| [2] |
Ali A, Hamouda W. Advances on spectrum sensing for cognitive radio networks:theory and applications[J]. IEEE Communications Surveys and Tutorials, 2017, 19(2): 1277-1304. DOI:10.1109/COMST.2016.2631080 |
| [3] |
Farag H M, Mohamed E M. Improved cognitive radio energy detection algorithm based upon noise uncertainty estimation[C]//2014 31st National Radio Science Conference (NRSC).[S. l.]: IEEE, 2014: 107-115.
|
| [4] |
Tandra R, Sahai A. SNR walls for signal detection[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1): 4-17. DOI:10.1109/JSTSP.2007.914879 |
| [5] |
Yu G, Shao Y, Long H, et al. Dynamic threshold based spectrum detection in cognitive radio systems[C]//2009 5th International Conference on Wireless Communications, Networking and Mobile Computing.[S. l.]: IEEE, 2009: 1-4. https://www.researchgate.net/publication/224609127_Dynamic_Threshold_Based_Spectrum_Detection_in_Cognitive_Radio_Systems
|
| [6] |
Martínez D M, Andrade Á G. On the reduction of the noise uncertainty effects in energy detection for spectrum sensing in cognitive radios[C]//2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC).[S. l.]: IEEE, 2014: 1975-1979. https://ieeexplore.ieee.org/document/7136495
|
| [7] |
Digham F F, Alouini M S, Simon M K. On the energy detection of unknown signals over fading channels[J]. IEEE Transactions on Communications, 2007, 55(1): 21-24. DOI:10.1109/TCOMM.2006.887483 |
| [8] |
Zhang W, Mallik R K, Letaief K B. Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2009, 8(12): 5761-5766. DOI:10.1109/TWC.2009.12.081710 |
| [9] |
Chen Y. Improved energy detector for random signals in gaussian noise[J]. IEEE Transactions on Wireless Communications, 2010, 9(2): 558-563. DOI:10.1109/TWC.2010.5403535 |
| [10] |
Singh A, Bhatnagar M R, Mallik R K. Performance of an improved energy detector in multihop cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(2): 732-743. DOI:10.1109/TVT.2015.2401332 |
| [11] |
Wang H, Xu Y, Su X, et al. Cooperative spectrum sensing in cognitive radio under noise uncertainty[C]//2010 IEEE 71st Vehicular Technology Conference (VTC 2010-Spring).[S. l.]: IEEE, 2010: 1-5. https://ieeexplore.ieee.org/document/5494009
|
| [12] |
Zhang R, Zhan Y, Pei Y, et al. Optimization of cooperative spectrum sensing under noise uncertainty[C]//2013 19th Asia-Pacific Conference on Communications (APCC).[S. l.]: IEEE, 2013: 393-397. https://ieeexplore.ieee.org/document/6765977
|
| [13] |
Ma Y, Gao Y, Zhang X, et al. Optimization of collaborating secondary users in a cooperative sensing under noise uncertainty[C]//2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC).[S. l.]: IEEE, 2013: 2502-2506. https://ieeexplore.ieee.org/document/6666567
|


