2. 上海电机学院 电子信息学院, 上海 201306;
3. 广西信息科学实验中心, 广西 桂林 541004
分析了多小区远程接入单元(RAU)个数、用户天线数、小区个数及发射功率等参数与系统下行链路能效(EE)最优时的关系.根据RAU与用户之间的距离,推导出系统吞吐量的解析式;根据具有路径损耗、阴影衰落、多径衰落特征的复合信道与多个实际功耗参数间的关系,建立了系统下行链路EE的优化模型;推导出系统EE与小区RAU个数、用户天线数、小区个数及发射功率的变化关系,并用算法得到了系统EE最优的理论值.理论分析和仿真结果验证了系统EE与影响其取值的多参数间关系的正确性,提出的系统EE优化算法具有迭代次数低的优点.
2. School of Electronic Information Engineering, Shanghai Dianji University, Shanghai 201306, China;
3. Guangxi Information Science Research Centre, Guangxi Guilin 541004, China
In multi-cell massive distributed wireless communication system, the relationship between the optimal downlink energy efficiency (EE) and the number of remote access units (RAUs), the number of user antennas, the number of cells and the transmitting power of multiple cells is studied. First, according to the distance between RAU and user, the analytic formula of system throughput is derived. Then, the downlink EE optimization model is established based on the relationship between the actual power consumption parameters and the composite channel, which includes path loss, shadow fading and multipath fading. Finally, based on this, the relationship between the EE and some impact factors including the number of RAUs, the number of user antennas, the number of cells and the transmitting power is deduced, meanwhile the corresponding algorithm is proposed to maximize the EE. Theoretical analysis and simulation results verify that the correctness of the relationship between system EE and multiple related parameters, and the proposed system EE optimization algorithm also has the advantage of low iteration times.
能源危机和环境污染使绿色通信成为下一代通信的关键,大规模多入多出(MIMO,multiple-input multiple-output)通信系统能显著提高能效(EE,energy efficiency),已成为移动通信领域的研究热点[1].但主要问题是大量天线部署在同一个基站上,信道相关性较强.大规模MIMO通信系统和分布式天线系统(DAS, distributed antenna systems)的结合能有效提高系统能效、频效,并显著减小信道相关性[2-3],成为新一代通信网络的关键技术.
DAS可以通过缩短发射机和用户之间的平均距离提高EE和覆盖范围[4],从而降低发射功率.与集中式天线系统(CAS, co-located antenna systems)相比,DAS能明显提高系统EE[5]. Joung等[6]通过设计预编码矩阵、天线选择矩阵和功率控制矩阵,最优化单小区大规模DAS的下行EE. Zuo等[7]研究了下行多小区大规模DAS的EE,在实际功耗模型下分别探讨了射频拉远头(RRH, remote radio head)个数、RRH天线数以及用户数对最大系统EE的影响. Wang等[8]在研究多小区DAS的EE时,通过连续的泰勒展开,将原问题转换成准凹分数形式的子问题,并提出算法使EE最优,但是在建立信道模型时仅考虑了大尺度信道衰落而忽略了小尺度衰落. Wu等[9]在研究多小区DAS功率分配的功耗模型时,仅考虑了发射功率和静态功率,没有考虑远程接入单元(RAU,remote access unit)的动态功率消耗. Gan等[10]证明了总发射功率和单个用户的速率会随着天线数目和用户数目趋于无穷时逐渐收敛,同时证明了EE与总发射功率和用户速率也呈现一种渐进关系.然而,实际上总发射功率并不仅仅是发射机的功率消耗,还包括静态功率消耗、电路动态功率消耗和回程功率消耗,所以在实际功耗模型中这种渐进关系并不可用. Castanheira和Gameiro[11]虽然在单小区DAS中讨论了处理额外分布式天线的开销,但其DAS的EE和发射功率的变化关系仍然不明确,难以在多小区DAS中推广.
就多小区大规模DAS而言,由于影响多小区大规模DAS系统EE的因素较多(包括用户天线数、小区RAU个数、最大发射功率等),目前在此方面进行研究的文献还较少[7].此外,一些文献在研究DAS的EE时,仅考虑理想化的功耗模型[9-10],虽能最大化系统EE,但却难以应用到实际场景中.
基于多小区大规模DAS下行链路系统EE的研究现状,针对文献[9-10]只考虑理想功耗模型的缺陷,构建了包含多个实际功耗参数的系统EE优化模型.同时基于提出的优化模型,研究分析了多小区RAU个数、用户天线数、小区个数及发射功率等参数与系统EE最优时的关系.还提出了低复杂度的优化算法,得到了系统EE的最优值.
1 系统能效优化模型 1.1 多小区大规模DAS模型主要考虑包含K个非协作小区下行大规模DAS,每个小区部署L个RAU,其中,第k个小区的第l个RAU表示为RAUlk,l∈{1, 2, …, L},k∈{1, 2, …, K},每个RAUlk配置M根天线. RAUlk是低功率和低消耗的基站,假设接收端信道状态信息完全已知,而发射端信道状态信息未知.假设RAU1k为当前小区的基带处理单元(BPU, baseband processing unit),主要功能是数据处理和进程管理,其他RAUlk(l≠1)通过光纤与其相连.为了简化分析,假设每个小区仅有一个用户(MS, mobile station),配置N根天线,可以同时接收多个RAUlk的发射信号.系统框图如图 1所示.
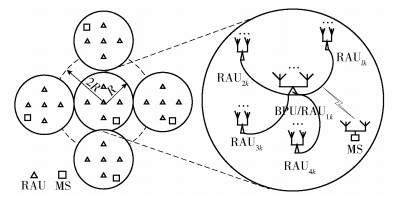
|
图 1 多小区大规模DAS系统框图 |
假设Xi=[xi1, xi2, …, xi(LM)]T为小区i中所有RAUlk对小区用户MSk的发送信号,则MSk接收信号为
| $ \boldsymbol{Y}_{k}=\boldsymbol{H}_{k k}\left(\boldsymbol{d}_{k k}\right) \boldsymbol{X}_{k}+\sum\limits_{i=1, i+k}^{K} \boldsymbol{H}_{i k}\left(\boldsymbol{d}_{i k}\right) \boldsymbol{X}_{i}+\boldsymbol{n} $ | (1) |
其中:第1项为MSk接收到的有用信号;第2项为其他小区对MSk的干扰信号;第3项n为加性高斯白噪声,满足E(nnH)=σnIN,σn为噪声功率;Hik(dik)=[Hlik(dlik), H2ik(d2ik), …, HLik(dLik)]为小区i中所有RAUlk到MSk的信道响应矩阵,dik=[d1,ik, d2,ik, …, dL,ik]T为小区i中所有RAUlk到MSk的距离向量.衰落信道矩阵Hlik(dlik)又可表示为[12]
| $ \boldsymbol{H}_{l i k}\left(d_{l i k}\right)=h_{s h, l i k} \boldsymbol{H}_{w, l i k} $ | (2) |
其中:Hw, lik为一个N×M维的小尺度衰落矩阵,其每个元素都服从复高斯分布;
假设小区形状是一个半径为R的圆,所有RAUlk的位置为沿圆环光纤回程均匀分布的DAS模型[12]. (qlk, θlk)为RAUlk相对于小区中心点的极坐标.考虑非本小区RAUli(i≠k)对MSk的干扰时,L个RAUli(i≠k)在半径为2R的圆中(以MSk小区中心为圆心),(qli, θli)为RAUli(i≠k)在2R圆中相对于中心点的极坐标. MSk均匀分布在小区中,MSk的极坐标为(ρ, θ).为分析方便,将(qlk, θlk)、(qli, θli)统一表示为(qlik, θlik),即表示小区i中第l个RAU相对小区k中心点的极坐标形式,从而可得第i个小区中的第l个RAU相对于MSk之间的距离为[13]
| $ {d_{lik}} = \sqrt {{\rho ^2} + q_{lik}^2 - 2\rho {q_{lik}}\cos \left( {\theta - {\theta _{lik}}} \right)} $ |
当i=k时,p(ρ)=2ρ/R2, p(θ)=1/2π,(qlik, θlik)=((3-
多小区DAS的功率消耗模型主要由静态功率消耗、电路动态功率消耗、传输功率消耗和回程功率消耗四部分组成,可以表示为[14-15]
| $ P_{\text { total }}=P_{\mathrm{FIX}}+M L P_{\mathrm{RAU}}+P_{\mathrm{t}} / \tau+P_{\mathrm{BH}} $ | (3) |
其中:PFIX为静态功率消耗部分;PRAU为每个RAU天线的动态功率要求;Pt为用户要求的发射功率;τ为功放因子;PBH为回程链路的功率消耗.
2 系统吞吐量及能效分析 2.1 基于互信息的系统吞吐量假设信道状态信息在发射端未知,而在接收端完全已知,采用等功率发送策略,则多小区大规模DAS中的小区用户MSk信道互信息可以表示为如下形式[13]:
| $ {I_k} = {\mathop{\rm lbdet}\nolimits} \left[ {{\mathit{\boldsymbol{I}}_M} + \gamma /N\mathit{\boldsymbol{H}}_{\rm{W}}^{\rm{H}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \oplus {\mathit{\boldsymbol{I}}_N}} \right){{{\mathit{\boldsymbol{H}}}}_W}} \right] $ | (4) |
其中:⊕表示克罗内克积,(*)H表示复共轭转置运算,γ=cPt/(Rασn2)表示信噪比.
| $ {{{\mathit{\boldsymbol{H}}}}_W} = \left[ {\begin{array}{*{20}{c}} {{{{\mathit{\boldsymbol{H}}}}_{W, 1}}}\\ {{{{\mathit{\boldsymbol{H}}}}_{W, 2}}}\\ \vdots \\ {{{{\mathit{\boldsymbol{H}}}}_{W, L}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\mathit{\boldsymbol{H}}}}_{w, 1kk}} + \sum\limits_{i = 1, i \ne k}^K {{{{\mathit{\boldsymbol{H}}}}_{w, 1ik}}} }\\ {{{{\mathit{\boldsymbol{H}}}}_{w, 2kk}} + \sum\limits_{i = 1, i \ne k}^K {{{{\mathit{\boldsymbol{H}}}}_{w, 2ik}}} }\\ \vdots \\ {{{{\mathit{\boldsymbol{H}}}}_{w, lkk}} + \sum\limits_{i = 1, i \ne k}^K {{{{\mathit{\boldsymbol{H}}}}_{w, Lik}}} }\\ {} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = \left[ {\begin{array}{*{20}{c}} {{{\left( {r/{d_{1kk}}} \right)}^\alpha }{S_{1kk}} + \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^\alpha }} {S_{lik}}}&0\\ \ddots &{}\\ 0&{{{\left( {r/{d_{Lkk}}} \right)}^\alpha }{S_{Lkk}} + \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{Lik}}} \right)}^\alpha }} {S_{Lik}}} \end{array}} \right] $ |
其中:r=R, D=2R.考虑大信噪比且N<ML,则式(4)可以表示为[13]
| $ \begin{array}{l} {I_k} = {\mathop{\rm lb}\nolimits} \;\det \left[ {{{{\mathit{\boldsymbol{I}}}}_M} + \gamma /N{{\mathit{\boldsymbol{H}}}}_W^{\rm{H}}\left( {{{\mathit{\boldsymbol{\Lambda }}}} \oplus {{{\mathit{\boldsymbol{I}}}}_N}} \right){{{\mathit{\boldsymbol{H}}}}_W}} \right] = \\ N{\rm{b}}\det \left[ {\gamma /N{{\mathit{\boldsymbol{H}}}}_W^{\rm{H}}\left( {{{\mathit{\boldsymbol{\Lambda }}}} \oplus {{{\mathit{\boldsymbol{I}}}}_N}} \right){{{\mathit{\boldsymbol{H}}}}_W}} \right] = N{\rm{b}}\gamma /N + \\ N\sum\limits_{l = 1}^L {{\rm{lb}}} \left[ {{{\left( {r/{d_{{\rm{l}}kk}}} \right)}^\alpha } + \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^\alpha }} } \right] + \\ N\sum\limits_{l = 1}^L {{\rm{lb}}{{\rm{S}}_{lik}}} + N{\rm{b}}\det {\left( {{{\mathit{\boldsymbol{H}}}}_{W, l}^{\rm{H}}{{{\mathit{\boldsymbol{H}}}}_{W, l}}} \right)^{\frac{1}{N}}} \end{array} $ | (5) |
其中
| $ \begin{array}{l} \;\;\;\;\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } \left[ {{{\left( {r/{d_{1kk}}} \right)}^\alpha } + \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^\alpha }} } \right] = \\ \sum\limits_{l = 1}^L {{\rm{lb}}} \left[ {{{\left( {\sqrt {{{\left( {r/{d_{1kk}}} \right)}^\alpha }} } \right)}^2} + {{\left( {\sqrt {\sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{ik}}} \right)}^\alpha }} } } \right)}^2}} \right] \ge \\ \;\;\;\;\;\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } \left[ {2{{\left( {r/{d_{1kk}}} \right)}^{\alpha /2}}\sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^{\alpha /2}}} } \right] = \\ L + \frac{1}{2}\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } {\left( {r/{d_{1kk}}} \right)^\alpha } + \frac{1}{2}\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^\alpha }} \end{array} $ |
| $ \begin{array}{l} {C_k} = E\left[ {{I_k}} \right] = N{\rm{lb}}\gamma /N + NL + \\ \;\;\;E\left[ {\frac{N}{2}\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } {{\left( {r/V{d_{1kk}}} \right)}^\alpha } + } \right.\\ \;\;\;\frac{N}{2}\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^\alpha }} ] + \\ E\left[ {N\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } {S_{lik}}} \right] + \prod\limits_{i = 1}^M {\frac{{\Gamma \left( {M - i + 1 + \frac{1}{N}} \right)}}{{\Gamma (M - i + 1)}}} \end{array} $ | (6) |
其中
| $ \begin{array}{l} \begin{array}{*{20}{c}} {E\left[ {\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } {{\left( {r/{d_{1kk}}} \right)}^\alpha }} \right] = }\\ {\frac{\alpha }{{2\ln 2}} + {\mathop{\rm lb}\nolimits} \sum\limits_{l = 1}^L {\exp } \left( { - \frac{{\alpha q_{lkk}^2}}{{2{r^2}}}} \right) = } \end{array}\\ \begin{array}{*{20}{c}} {\frac{\alpha }{{2\ln 2}} + {\mathop{\rm lb}\nolimits} L + {\mathop{\rm lb}\nolimits} \exp \left( { - \frac{{6 - 3\sqrt 3 }}{4}} \right)}\\ {E\left[ {\sum\limits_{l = 1}^L {{\mathop{\rm lb}\nolimits} } \sum\limits_{i = 1, i \ne k}^K {{{\left( {D/{d_{lik}}} \right)}^\alpha }} } \right] = } \end{array}\\ \begin{array}{*{20}{c}} {(K - 1)\left( {\frac{\alpha }{{2\ln 2}} + {\rm{lb}}L + {\rm{ lbexp }}( - (6 - 3\sqrt 3 ))} \right)}\\ {\qquad E\left[ {{S_{lik}}} \right] = \exp \left( {\frac{1}{2}{\lambda ^2}\sigma _{sh}^2} \right)} \end{array} \end{array} $ |
综上,在大信噪比且N < ML下,小区用户MSk平均信息量为[13]
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{C_k} = N\left[ {{\rm{ lb }}\gamma /N + L + \frac{{K\alpha }}{{4\ln 2}} + \frac{K}{2}{\mathop{\rm lb}\nolimits} L + } \right.}\\ {\qquad \frac{{{\lambda ^2}\sigma _{sh}^2}}{{2\ln 2}} + {\mathop{\rm lb}\nolimits} \exp \left( { - \frac{{6 - 3\sqrt 3 }}{8}} \right) + } \end{array}\\ \begin{array}{*{20}{c}} {(K - 1){\rm{ lbexp }}\left( { - \frac{{6 - 3\sqrt 3 }}{2}} \right) + }\\ {\sum\limits_{i = 1}^M \Gamma \left( {M - i + 1 + \frac{1}{N}} \right) - \sum\limits_{i = 1}^M \Gamma (M - i + 1)]} \end{array} \end{array} $ | (7) |
其中Γ(·)表示伽马函数.
2.2 系统能效解析式由式(3)和式(7)可得多小区大规模DAS系统小区用户MSk下行链路的EE式为[17]
| $ \begin{array}{l} {\xi _{{\rm{EE}}}} = \frac{{{C_k}}}{{{P_{{\rm{ total }}}}}} = \frac{N}{{{P_{{\rm{FIX}}}} + ML{P_{{\rm{RAU}}}} + {P_t}/\tau + {P_{{\rm{BH}}}}}} \times \\ \left[ {{\mathop{\rm lb}\nolimits} \gamma /N + L + \frac{{K\alpha }}{{4\ln 2}} + \frac{K}{2}{\mathop{\rm lb}\nolimits} L + \frac{{{\lambda ^2}\sigma _{sh}^2}}{{2\ln 2}} + } \right.\\ \begin{array}{*{20}{c}} {{\rm{ lb}}\;{\rm{exp }}\left( { - \frac{{6 - 3\sqrt 3 }}{8}} \right) + }\\ {(K - 1){\rm{lb}}\;\exp \left( { - \frac{{6 - 3\sqrt 3 }}{2}} \right) + } \end{array}\\ \sum\limits_{i = 1}^M \Gamma \left( {M - i + 1 + \frac{1}{N}} \right) - \sum\limits_{i = 1}^M \Gamma (M - i + 1)] \end{array} $ | (8) |
式(8)中多小区大规模DAS系统中,小区用户下行链路的EE与RAU个数、用户天线数、小区个数及发射功率等多种因素相关,下面将研究分析其中单个参数对EE的影响.
3.1 能效与RAU个数的关系引理1 在RAU个数L的取值范围内EE优解.
证明 根据式(8),有
| $ \frac{{\partial {\xi _{{\rm{EE}}}}}}{{\partial L}} = \frac{{\frac{{NK{P_{{\rm{total}}}}}}{{2L\ln 2}} - {C_k}M{P_{{\rm{RAU}}}} + 1}}{{P_{{\rm{total}}}^2}} $ | (9) |
其中:分母为正数,所以式(9)的正负完全由分子决定.
令
| $ \begin{array}{l} \frac{{\partial \zeta (L)}}{{\partial L}} = \frac{{2L\ln 2NKM{P_{{\rm{RAU}}}} - 2\ln 2N{P_{{\rm{total}}}}K}}{{{{(2L\ln 2)}^2}}} - \frac{{NMK{P_{{\rm{RAU}}}}}}{{2L\ln 2}} = \\ - \frac{{NK}}{{2{L^2}\ln 2}}\left( {{P_{{\rm{FXX}}}} + {P_{\rm{t}}}/\tau + {P_{{\rm{BH}}}}} \right) - \frac{{MNK{P_{{\rm{RAU}}}}}}{{2L\ln 2}} < 0 \end{array} $ | (10) |
式(10)表明,ζ(L)取值随L增加而递减,且满足
由引理1可知,小区用户MSk下行链路EEARAU个数L的增加满足先增后减的关系,即RAU取适当值时会使EE最优.这是由于虽然功耗会随RAU个数递增,但是当RAU较少时,系统和速率随RAU增加的速度大于功耗增加的速度使EE增加;当RAU个数增加到大于使EE最优的RAU个数时,此时系统和速率的增加不足以弥补因过多RAU开销而造成的功率消耗使EE降低.
3.2 能效与用户天线数的关系用户天线数也是影响EE的关键因素,通过式(8)能得到如下引理.
引理2 EE在用户天线数N的取值范围内存在最优解.
证明 由式(8),对ξEE关于N求导得
| $ \frac{{\partial {\xi _{{\rm{EE}}}}}}{{\partial N}} = \frac{1}{{{P_{{\rm{ total }}}}}}\left( {\frac{{{C_k}}}{N} - \frac{1}{{\ln \;2}} - \sum\limits_{i = 1}^M {\int_0^\infty {\frac{{{t^{\frac{1}{N} + M - i}}\ln t}}{{\exp (t)}}} } {\rm{d}}t} \right) $ |
令
由引理2可知,接收端的天线数目并非越多越好,其和EE存在折中关系,通过寻找最优用户天线数,可使EE达到最优值,当天线数目超过或小于这个最优天线数时,EE降低.
3.3 能效与小区个数的关系多小区大规模DAS系统中,小区用户MSk下行链路的EE,在不考虑覆盖范围的情况下,与小区个数存在线性关系.结论如引理3.
引理3 当RAU个数L>exp (
证明 由式(8),对ξEE关于K求导并令其小于0得L>exp (
引理3表明,在不考虑覆盖范围的情况下,EE会随着小区个数递增(大规模DAS系统的RAU个数L一定会大于exp (
从式(8)可以看出,EE解析式的分子和分母均与发射功率有关,相关结论如引理4所示.
引理4 EE在发射功率Pt的取值范围内存在最优解.
证明式(8)对Pt求导得
| $ \frac{{\partial {\xi _{{\rm{EE}}}}}}{{\partial {P_{\rm{t}}}}} = \frac{{\frac{{N{P_{{\rm{total}}}}}}{{{P_{\rm{t}}}\ln 2}} - \frac{{{C_k}}}{\tau }}}{{P_{{\rm{total}}}^2}} $ |
令
| $ \frac{{\partial \mathit{\Psi} \left( {{P_{\rm{t}}}} \right)}}{{\partial {P_{\rm{t}}}}} = - \frac{{Nln2\left( {{P_{{\rm{FIX}}}} + ML{P_{{\rm{RAU}}}} + {P_{{\rm{BH}}}}} \right)}}{{{{\left( {{P_{\rm{t}}}\ln 2} \right)}^2}}} - \frac{{N{P_{{\rm{total}}}}}}{{\tau {P_{\rm{t}}}\ln 2}} < 0 $ |
可见Ψ(Pt)关于变量Pt递减,并满足
引理4表明,发射功率增加可提高EE,但增加到一定值时EE会下降.这是由于当发射功率较小时,系统容量增长的速率大于发射功率的增长速率,此时容量的增加足以补偿实际功耗的增加,使EE增大.当发射功率继续增加到一个特定值时,容量的增加刚好可以满足实际功耗的增加,使EE最大.之后,继续增加最大发射功率,系统容量的增加不足以补偿实际功耗的增加而导致EE降低.
4 能效优化法设计由引理1、引理2、引理4可知,大规模DAS系统中小区用户MSk下行链路的EE与RAU个数、用户天线数以及最大发射功率等多个参数有关,单个参数下EE最大值并非是系统整体EE的最大值,这些参数只有满足一定的均衡关系才能使EE最优.因此,本节分别通过算法1、算法2、算法3的分析设计寻求EE最优时,RAU个数、用户天线数以及最大发射功率的值.
在寻求最优RAU个数时,RAU的个数不能超过可利用射频链的个数[18],所以可以利用射频链的个数作为寻求RAU个数的终止条件.同时,因为RAU的个数只能为整数,所以在设置迭代步长时可以把步长设置为1.综上,寻求最优RAU个数的算法1描述如下:
步骤1 初始化l=1,ξEE(l)=0,同时设射频链的个数为SL;
步骤2 当l<SL,则l′=l+1,根据公式(8)计算ξEE(l′);
步骤3 如果ξEE(l′)≤ξEE(l),则此时的l和ξEE(l)为最优值,直接输出;
步骤4 否则更新l=l′, ξEE(l)=ξEE(l′),然后跳转到步骤2.
类似上述分析,在寻求EE最优下用户天线数目时,把系统可连接的最大用户天线数作为终止条件,且设置步长为1,寻求EE最优时用户天线数的算法2描述如下.
步骤1 初始化n=1,ξEE(n)=0,同时设系统可连接的最大用户天线个数为SN;
步骤2 当n<SN,则n′=n+1,并根据式(8)计算ξEE(n′);
步骤3 如果ξEE(n′)≤ξEE(n),则此时的n和ξEE(n)为最优值,直接输出;
步骤4 否则更新n=n′,ξEE(n)=ξEE(n′),然后跳转到步骤2.
发射功率设置过大不仅不能提高系统EE,反而造成资源浪费,导致更坏的系统表现,因此系统通常会设置一个最大发射功率的阈值,可以把阈值作为EE最优时寻求最优发射功率终止条件,并设置适当的步长,可得到算法3:
步骤1 初始化p=1,ξEE(p)=0,同时设系统最大发射功率的阈值为SPt;
步骤2 当p<SPt,则p′=p+ν,并根据式(8)计算ξEE(p′);
步骤3 如果ξEE(p′)≤ξEE(p),则此时的p和ξEE(p)为最优值,直接输出;
步骤4 否则更新p=p′,ξEE(p)=ξEE(p′),然后跳转到步骤2.
算法1、算法2设置步长为1,且RAU个数和用户天线数并非无限增加,因此算法1、算法2能以较少的迭代次数寻求出最优结果.算法3通过合理设置步长ν也能快速找到最优解.因此,上述算法在实际应用中不会额外增加过多开销,且易于实现.
假设以上算法中步骤2的最大截止条件为κ(κ为SL、SN或者SPt),如果算法迭代在最大截止条件处结束,则复杂度为ο(κ).但若算法满足步骤3中的条件,迭代就会提前结束而输出最优值,此时的迭代次数用Φ表示,则实际算法的复杂度ο(Φ)≤ο(κ).
5 仿真结果与分析系统仿真环境参数设置为[7, 19]:小区半径为1 km,噪声功率为-104 dBm,发射功率Pt为46 dBm,路径损耗因子为3.7,功放因子τ为0.4.静态功率消耗PFIX=9 W,回程链路的功率消耗PBH=0.2 W,每个RAU天线的动态功率要求PRAU=2 W,平均路径增益的中值c=1,阴影衰落因子的功率σsh2=10.
图 2为不同RAU个数下EE的值.由图 2可以看出,随RAU个数L的增加,EE先递增后递减,即在RAU个数L取值范围内EE存在最优解,与引理1相符.从图 2中还可以看出:①当RAU个数L与用户天线数N确定时,EE随小区个数K的增加逐渐增大;②当RAU天线数M与小区个数K一定时,EE随用户天线数N的增加而提高.
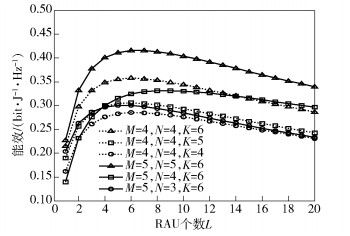
|
图 2 不同RAU个数下EE值 |
图 3为不同用户天线数下EE的值.由图 3可以看出,EE随用户天线数N的总体变化趋势先增后减,即在用户天线数N的取值范围内EE存在最优解.从图 3中还可以看出:当小区个数K及发射功率Pt确定时,EE会随着RAU个数L的增加而递增.
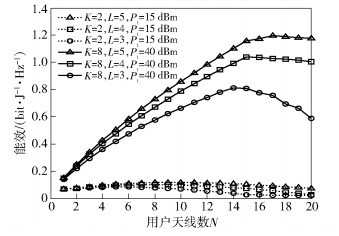
|
图 3 不同用户天线数下EE |
图 4(a)为EE与不同用户天线数和RAU个数的关系.可以看出,在用户天线数为15,RAU个数为7时,EE达到了最优.图 4(b)为EE与不同RAU个数和发射功率Pt的关系.可以看出,EE在RAU个数为4,发射功率为6 dBm时达到最大.
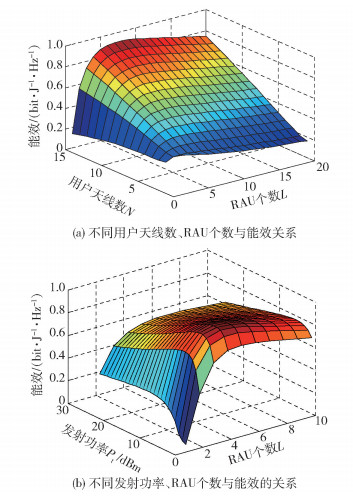
|
图 4 系统EE与多参数的关系 |
图 5为小区个数K和EE之间的仿真关系.由图 5可以看出,EE随小区个数K成线性递增关系.但是,在实际设计中,考虑到小区覆盖范围以及控制成本,小区个数K并不能设置过大,要结合RAU个数、用户天线数N以及发射功率Pt合理的折中.
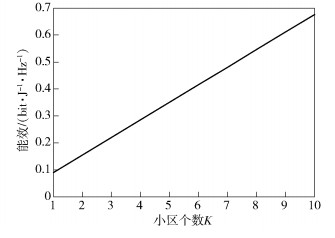
|
图 5 小区个数和能效之间的关系 |
图 6为不同发射功率Pt下EE的值.由图 6可以看出,EE随发射功率Pt先增后减,即EE在发射功率Pt的取值范围内存在最优解.从图 6中还可以看出:①当RAU个数为固定不变(L=6)时,EE随用户天线数N的递增而增加;②当用户天线数固定不变(N=4)时,EE随RAU个数L的递增而下降.
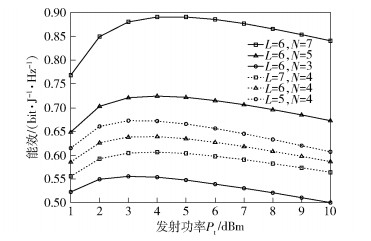
|
图 6 不同发射功率下EE值 |
从上述仿真图中还可以看出,多小区大规模DAS系统下行链路系统EE较小,这主要是因为仿真中参数选取限定在较小范围内.此外,为简化分析,EE在理论分析和仿真时也仅考虑了单个用户而非多用户时的场景.
6 结束语在实际信道模型和功耗模型下,研究大规模DAS系统下行链路EE随小区RAU个数、用户天线数、小区个数以及发射功率之间的变化关系,并基于RAU与用户之间的距离提出算法求解最优RAU个数、最优用户天线数以及最优发射功率以最大系统EE.理论和仿真结果均证明这种关系的正确性, 而且提出的算法能以较低的迭代次数得到最优解.此外,本文的算法及结论是在理想信道状态下得出的,实际信道模型及通信场景中的算法和结论尚需进一步研究.
| [1] |
Ngo H Q, Larsson E G, Marzetta T L. Energy and spectral efficiency of very large multiuser MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(4): 1436-1449. DOI:10.1109/TCOMM.2013.020413.110848 |
| [2] |
Liu An, Lau V K N. Joint power and antenna selection optimization in large cloud radio access networks[J]. IEEE Transactions on Signal Processing, 2014, 62(5): 1319-1328. DOI:10.1109/TSP.2014.2298367 |
| [3] |
Truong K T, Heath R W. The viability of distributed antennas for massive MIMO systems[C]//Asilomar Conference on Signals, Systems and Computers. New York: IEEE Press, 2013: 1318-1323.
|
| [4] |
Lin Dai. An uplink capacity analysis of the distributed antenna system (DAS):from cellular DAS to DAS with virtual cells[J]. IEEE Transactions on Wireless Communications, 2014, 13(5): 2717-2731. DOI:10.1109/TWC.2014.033114.130557 |
| [5] |
He Chunlong, Sheng Bin, Zhu Pengcheng, et al. Energy efficient comparison between distributed MIMO and co-located MIMO in the uplink cellular systems[C]//IEEE Vehicular Technology Conference. New York: IEEE Press, 2012: 1-5.
|
| [6] |
Joung J, Chia Y K, Sun S M. Energy-efficient, large-scale distributed-antenna system (L-DAS) for multiple users[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 954-965. DOI:10.1109/JSTSP.2014.2309942 |
| [7] |
Zuo Jun, Zhang Jun, Yuen C, et al. Energy-efficient downlink transmission for multicell massive DAS with pilot contamination[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 1209-1221. DOI:10.1109/TVT.2016.2555842 |
| [8] |
Wang Jing, Feng Wei, Chen Yunfei, et al. Energy efficient power allocation for multicell distributed antenna systems[J]. IEEE Communications Letters, 2016, 20(1): 177-180. DOI:10.1109/LCOMM.2015.2498608 |
| [9] |
Wu Jiang, Liu Jianwei, Li Wanlin, et al. Low-complexity power allocation for energy efficiency maximization in DAS[J]. IEEE Communications Letters, 2015, 19(6): 925-928. DOI:10.1109/LCOMM.2015.2415781 |
| [10] |
Gan Ransong, Li Yunzhou, Zhou Shidong, et al. On sum rate of multi-user distributed antenna system with circular antenna layout[C]//IEEE Vehicular Technology Conference. New York: IEEE Press, 2007: 596-600.
|
| [11] |
Castanheira D, Gameiro A. Distributed antenna system capacity scaling:coordinated and distributed MIMO[J]. IEEE Wireless Communications, 2010, 17(3): 68-75. DOI:10.1109/MWC.2010.5490981 |
| [12] |
Wang Xinzheng, Zhu Pengcheng, Chen Ming. Antenna location design for generalized distributed antenna systems[J]. IEEE Communications Letters, 2009, 13(5): 315-317. DOI:10.1109/LCOMM.2009.090123 |
| [13] |
Wang Dongming, Wang Jiangzhou, You Xxiaohu, et al. Spectral efficiency of distributed MIMO systems[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(10): 2112-2127. DOI:10.1109/JSAC.2013.131012 |
| [14] |
Björnson E, Sanguinetti L, Hoydis J, et al. Optimal design of energy-efficient multi-user MIMO systems:is massive MIMO the answer?[J]. IEEE Transactions on Wireless Communications, 2015, 14(6): 3059-3075. DOI:10.1109/TWC.2015.2400437 |
| [15] |
Arnold O, Richter F, Fettweis G, et al. Power consumption modeling of different base station types in heterogeneous cellular networks[C]//Future Network and Mobile Summit. New York: IEEE Press, 2011: 1-8.
|
| [16] |
Tulino A M, Verdú S. Random matrix theory and wireless communications[J]. Communication and Information Theory, 2004, 1(1): 1-182. |
| [17] |
Isheden C, Chong Z, Jorswieck E, et al. Framework for link-level energy efficiency optimization with informed transmitter[J]. IEEE Transactions on Wireless Communications, 2012, 11(8): 2946-2957. |
| [18] |
He Chunlong, Li G Y, Zheng Fuchun, et al. Energy efficiency of distributed MIMO systems[C]//IEEE Global Conference on Signal and Information Processing. New York: IEEE Press, 2014: 218-222.
|
| [19] |
Onireti O, Heliot F, Imran M A. On the energy efficiency-spectral efficiency trade-off of distributed MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(9): 3741-3753. DOI:10.1109/TCOMM.2013.071813.120823 |


