2. 北京邮电大学 信息与通信工程学院, 北京 100876;
3. 郑州大学 信息工程学院, 郑州 450001
将能量采集技术与大规模无线协作通信网络相结合,分析了在信息与能量同传环境下,大规模无线协作通信网络的中断性能.提出了一种中继协作传输协议,将位于源节点的中继区域内,并且能够成功解码源节点信号的中继节点定义为潜在中继,潜在中继用于协助从源节点到目的节点的信息传输;通过随机几何的数学工具,进一步分析了接收端使用选择合并接收方式下的中断性能,并对比了协作链路、中继链路以及直接链路三者的中断概率;最后对理论分析结果进行了仿真验证.验证的结果表明,最优中继策略下的中断性能最优.
2. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China
The outage probability in a large-scale cooperative relaying system based on simultaneous wireless information and power transfer (SWIPT) is investigated. A relay-assisted cooperative transmission protocol is proposed in which the relays that can decode the signal from the sources and are located in a relaying area become the potential relays, and are dedicated to assist the information transmission from the sources to the receivers. The outage probability is analyzed and the comparison is made among the direct link, the relay-only link, and the cooperative link. Simulation results are provided to validate our theoretical analysis.
近年来,由于能源需求呈指数型增长,能源和环境问题成为当下国内外共同关注的热点.无线通信产业在实现绿色通信方面占据着至关重要的位置,其中一项重要的技术就是能量采集技术.该技术可以使无线设备从周边环境中的可再生能源中收集能量,不仅可以延长无线节点的生命周期,还能够有效地降低二氧化碳的排放水平[1].但是,由于风能、太阳能等可再生能源受限于空间、时间等因素,对于一些地理位置比较复杂的能源节点来说,电池续电问题仍旧是一个比较大的挑战.随着对射频(RF, radio frequency)电磁波理论探索的逐渐深入,采集RF能量在技术上也取得了重大进展[2],相对可再生能源到达的随机性来说,收集射频能量具有较强的可控性,能够较好地克服无线通信网络中设备面临的电池替换不灵活,能量短缺等难题.
无线射频信号能够同时承载信息和能量,给能量采集和信息传输的同时执行提供了理论可能[2],这种有着很大潜力的技术被称作无线信息和能量同传(SWIPT, simultaneous wireless information and power transfer),也可以称作无线携能通信;这给无线系统的设计带来了历史性的变革. Varshney[3]在2008年第1次提出了SWIPT的概念,鉴于现有的接收机不能在信息解码的同时从同一信号中提取能量,Zhou等[4]把中继节点接收到的信号流动态地分成2个功率流,分别用以信息解码和能量采集.
对于能量受限的网络来说,将基于RF能量采集技术引入无线协作通信网络当中,可以进一步提升网络性能[2],也是未来通信系统中非常有前景的技术之一. Nasir等[5]研究了基于功率分割和基于时间切换技术的中继协议,在中继节点处实现信息与能量的同传,并分析了系统的中断性能. Liu等[6]分析了携能通信技术在正交频分复用中继系统中的应用.
近年来,由于随机几何[7]理论具有能够对随机网络节点位置建模和计算网络中的干扰等优势,已成功提供了一个统一的数学范例来建模和分析大规模无线通信网络. Huang[8]通过使用随机几何工具来分析基于RF能量采集驱动的移动自组织网络容量. Lee[9]研究了基于RF能量采集的认知无线网络,次网络发射机通过采集主网络传输的RF信号为自身供电,并且寻找频谱机会进行数据传输.
现有这些结合RF能量采集技术和协作中继技术的研究工作仍存在一定的局限性:1)已有工作大部分考虑的都是针对点对点,或点对多点的协作网络配置,很少考虑大规模无线协作通信网络;2)在协作中继系统中,很多学者假设中继节点的位置或者中继节点与收发机节点之间的距离都是固定的;例如,Nasir[5]和Liu等[6]假设中继节点和目的节点之间的距离是一个固定值.
考虑一个大规模无线协作通信网络,该网络由随机分布的“源-目的”节点对和中继节点组成.中继节点通过收集源节点广播的RF能量为自身供电.提出了一个中继协作传输协议,在第1阶段,中继节点将收到源节点传输的RF信号分成2部分,分别用于能量采集和信息解码;位于源节点中继区域内,并且可以成功解码源节点传输信息的中继成为潜在中继,专门协助源节点到目的节点的信息传输.在第2阶段,分别考虑随机中继选择策略(RRS, random relay selection)和最优中继选择策略(BRS, best relay selection),被选中的中继节点将信息转发至目的节点,并将协作链路下的中断概率与直接链路、中继链路的中断性能进行了对比.
1 系统模型及传输协议 1.1 系统模型研究一个分布在二维空间上的大规模无线协作通信网络,该网络是由多个“源-目的”节点对和随机分布的中继节点组成.假设所有源节点的位置分布服从均匀的泊松点过程(HPPP, homogeneous poisson point processes),用符号Θt表示,密度为μt.对于每一个源节点来说,其关联接收机(目的节点)位于距离其d1远的某个随机位置处.假设网络中所有中继节点的位置分布都服从密度为μr的HPPP,用符号Θr表示.另外,所有的源节点有稳定的能量来源,传输功率为Ps;中继节点没有固定的能量来源,只能从源节点发送的RF信号中收集能量为自身供电.利用收集到的能量,中继节点协助源节点将信息转发至其关联接收机.
假设传播衰落信道建模为小尺度瑞利衰落和大尺度路径损耗的乘积,表示为
| $ g(r) = {h_k}{\left\| {{x_1} - {x_2}} \right\|^{ - \alpha }} $ | (1) |
其中:hk表示信道功率衰落系数,服从指数分布;‖·‖是欧氏距离;α则是路径损耗指数,α>2.
1.2 传输协议提出了一个中继协作传输协议,基于该协议,传输过程共要经历2个阶段,分别对应在2个时隙内进行,并且假设时间在每个时隙中都被归一化.
1) 广播阶段
在第1阶段,所有的源节点同时进行信号广播,中继节点将接收到的RF信号流分成两部分,其中一部分收集能量,用来为自身节点供能;另一部分用来进行信息接收,其中,功率分割系数用ρ (0 <ρ < 1)表示.
如图 1所示,每个源节点定义了一个选择区域,用符号
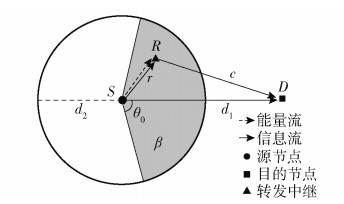
|
图 1 系统场景 |
2) 转发阶段
在第2阶段,假若源节点的选择区域内存在满足条件的潜在中继集,则选定其中一个中继节点完成源节点到目的节点的信息转发.考虑2种不同的中继选择策略,分别为随机中继选择策略和最优中继选择策略,被选中的中继节点将信息转发至关联接收机[10].
随机中继选择策略,即从潜在中继集中以相等的概率随机选择一个中继节点完成第2阶段的转发过程;而最优中继选择策略则是从潜在中继集中选择信号强度最好的中继节点进行转发,即满足以下条件:
| $ R = \mathop {\arg \max }\limits_{{x_k} \in {\mathit{\Theta} _{rp}}} \left\{ {{h_{kD}}{{\left\| {{x_k} - {x_D}} \right\|}^{ - \alpha }}} \right\} $ | (2) |
其中:Θrp表示满足条件的潜在中继集,hkD表示中继节点xk到目的节点xD之间的信道功率衰落系数.
1.3 度量准则中断概率为目的节点不能够从其相应的源节点成功解码接收到的信号的概率.一般地,给出接收机信干噪比(SINR, signal-to-interference-plus-noise ratio),用符号Ω表示,相应的目标SINR用符号γ表示,网络的中断概率定义为
| $ {O_{{\rm{ out }}}} = \Pr \{ \mathit{\Omega} < \gamma \} $ | (3) |
下面根据提出的中继协作传输协议,对系统的中断性能进行理论推导和分析.基于源节点所构成的泊松点过程的平稳性,考虑在原点处存在一个典型的源节点S,并给定其关联目的节点D位于距离其d1远的某个随机位置上,如图 1的拓扑结构所示. R表示已经选择的中继节点.基于Slivnyak定理[11],可以得到剩余的“源-目的”节点对构成的点过程同样服从节点密度为μt的HPPP.
2.1 直接链路下面首先分析在源-目的节点之间不存在协作转发过程的直接链路通信,则该通信过程在一个时隙内完成.所有源节点同时向其相关联目的节点发送信息.因此,典型目的节点D处的SINR由下式给出:
| $ {\mathit{\Omega} _0} = \frac{{{P_s}{h_0}d_1^{ - \alpha }}}{{{P_s}{I_0} + {\sigma ^2}}} $ | (4) |
| $ {I_0} = \sum\limits_{{x_k} \in {\mathit{\Theta} _t}} {{h_{{x_k}}}} {\left\| {{x_k} - {x_D}} \right\|^{ - \alpha }} $ | (5) |
其中:I0表示在节点D处收到的来自所有源节点的聚合干扰,h0和hxk则分别表示链路节点S到节点D以及剩余源节点xk到D的信道功率衰落系数,xD表示节点D的坐标,σ2表示高斯白噪声功率,Θt表示所有源节点的集合.由式(3)可以得到下面的定理.
定理1 直接链路通信下的网络中断概率Od(Ps, γ)为
| $ {O_d}\left( {{P_s}, \gamma } \right) = 1 - \exp \left( { - \frac{{{\sigma ^2}\gamma d_1^\alpha }}{{{P_s}}}} \right)\exp \left( { - {\mu _t}\kappa d_1^2{\gamma ^{\frac{2}{\alpha }}}} \right) $ | (6) |
其中
对于中继链路来说,整个传输过程需要分成2个阶段,分别对应在2个时隙内完成.
1) 在第1阶段,已经选定的转发中继节点R将收到的源节点传输的RF信号流分成两部分,其中一部分收集能量,用来为自身节点供能,另一部分用来进行信息接收,功率分割因子表示为ρ.在转发中继节点R处的SINR以及从源节点处采集到的功率分别表示为
| $ {\mathit{\Omega} _1} = \frac{{(1 - \rho ){P_s}{h_1}{r^{ - \alpha }}}}{{(1 - \rho ){P_s}{I_t} + {\sigma ^2}}} $ | (7) |
| $ {P_r} = \eta E\left[ {\rho {P_s}\left( {{h_1}{r^{ - \alpha }} + {I_t}} \right)} \right] $ | (8) |
| $ {I_t} = \sum\limits_{{x_t} \in {\mathit{\Theta} _t}} {{h_{{x_t}}}} {\left\| {{x_t} - {x_R}} \right\|^{ - \alpha }} $ | (9) |
其中:It表示在节点R收到的聚合干扰,η(0 <η≤1)表示能量采集效率,r为源节点S与中继节点R的传输距离,h1和hxt则分别表示链路节点S到节点R以及xt到节点R的信道功率衰落系数,xR表示节点R的坐标.
假设时间在每个时隙中被归一化,因此能量可以等价于功率.另外假设中继节点以可变功率进行传输,并且使用收集到的所有能量完成下一步的转发传输.
定义Θsp表示能够成功解码源节点传输信息的中继集,则成功解码的概率可以表示为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{{\rm{sec}}}} = \Pr \left\{ {{\mathit{\Omega} _1} \ge \gamma } \right\} = \\ {E_r}\left[ {\exp \left( { - \frac{{{\sigma ^2}\gamma {r^\alpha }}}{{(1 - \rho ){P_s}}}} \right)\exp \left( { - {\mu _t}\kappa {r^2}{\gamma ^{\frac{2}{\alpha }}}} \right)} \right] \end{array} $ | (10) |
因此得到集合Θsp的密度为μtpsec.
根据泊松点过程的基本特性
| $ \begin{array}{l} \;\;\;\;\;\;\;{O_e} = \exp \left( { - \int_{{\mathscr{B}}} {{\mu _t}} {p_{\sec }}{\rm{d}}x} \right) = \\ {\mu _i}\exp \left( { - \int_{ - {\theta _0}}^{{\theta _0}} {\int_0^{{d_2}} {\exp } } \left( { - \frac{{{\sigma ^2}\gamma {r^\alpha }}}{{(1 - \rho ){P_s}}}} \right) \times } \right.\\ \;\;\;\;\;\;\exp \left( { - {\mu _\iota }\kappa {r^2}{\gamma ^{\frac{2}{\alpha }}}} \right)r{\rm{d}}r{\rm{d}}\theta ) \end{array} $ | (11) |
因此,所有被选中继节点(位于中继区域
2) 在第2阶段,根据随机中继选择方案,即选中的中继节点(如图 1中的节点R),以传输功率Pr进行下一阶段的信息传输.其中Pr由式(8)得到.因此,在目的节点D处的SINR可以表示为
| $ {\mathit{\Omega} _2} = \frac{{{P_r}{h_2}{c^{ - \alpha }}}}{{{P_r}{I_r} + {\sigma ^2}}} $ | (12) |
| $ {I_r} = \sum\limits_{{y_r} \in {\mathit{\Theta} _{rs}}} {{h_{{y_r}}}} {\left\| {{y_r} - {x_D}} \right\|^{ - \alpha }} $ | (13) |
其中:Ir表示在节点D处收到的来自所有中继节点yr的干扰,c表示中继节点R与接收机D之间的距离,表示为
相应地,中继链路的中断概率可以表示为
| $ \begin{array}{l} {O_r}\left( {{P_r}, \gamma } \right) = \Pr \left\{ {{\mathit{\Omega} _2} < \gamma } \right\} = 1 - \int_{\mathscr{B}} {\exp } \left( { - \frac{{{\sigma ^2}\gamma {c^\alpha }}}{{{P_r}}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\exp \left( { - {\mu _t}\left( {1 - {O_e}} \right)\kappa {c^2}{\gamma ^{\frac{2}{\alpha }}}} \right){\rm{d}}x \end{array} $ | (14) |
值得一提的是,目的节点通过选择合并(SC, selection combining)方式[12]对收到的两路信号进行合并.选择合并方案的目的节点合并器将输出具有最高SINR链路上的信号.选择合并只需要相应的SINR测量值,不需要精确的信道状态信息.则选择合并方案下,协作链路发生中断的情况有2种可能:①直接链路中断,且源节点的中继区域内没有符合条件的中继节点完成信息转发;②直接链路中断,中继节点成功解码源节点传输的信号,但是,第2阶段中继链路也发生了中断.因此,可以得出下面的结论.
1) 中继链路中断概率.中继链路发生中断的条件为:①源节点的中继区域内没有符合条件的中继节点完成信息转发; ②存在符合条件的转发中继节点,但是第2阶段发生了中断.因此,中断概率表示为
| $ {O_{r, {\rm{RRS}}}} = \underbrace {{O_e}}_{{\rm{case}}\;a} + \underbrace {\left( {1 - {O_e}} \right){O_r}\left( {{P_r}, \gamma } \right)}_{{\rm{ case }}\;b} $ | (15) |
2) 协作链路中断概率.根据以上分析的协作链路发生中断的条件,得到协作链路的中断概率为
| $ \begin{array}{*{20}{c}} {{O_{c, {\rm{RRS}}}} = {O_d}\left( {{P_s}, \gamma } \right){O_e} + }\\ {{O_d}\left( {{P_s}, \gamma } \right)\left( {1 - {O_e}} \right){O_r}\left( {{P_r}, \gamma } \right)} \end{array} $ | (16) |
在最优中继选择策略下,第1阶段的过程与随机选择中继策略的过程一致;在第2阶段,从潜在中继集中选择信号强度最好的中继节点进行转发.前面已经假设了所有被选中继节点形成的泊松点过程Θrs,相应地,根据式(2),得到第2阶段的中断概率为
| $ \begin{array}{*{20}{c}} {O_r^\prime \left( {{P_r}, \gamma } \right) = \exp \left( { - \int_{ - {\theta _0}}^{{\theta _0}} {\int_0^{{d_2}} {\left( {\exp \left( { - \frac{{\gamma {\sigma ^2}{c^\alpha }}}{{{P_r}}}} \right) \times } \right.} } } \right.}\\ {\exp \left( { - {\mu _t}\left( {1 - {O_e}} \right)\kappa {c^2}{\gamma ^{\frac{2}{\alpha }}}} \right))r{\rm{d}}r{\rm{d}}\theta )} \end{array} $ | (17) |
由此,可以得到以下结果.
1) 中继链路中断概率.与随机中继选择策略相同,表示为
| $ {O_{r, {\rm{BRS}}}} = {O_e} + \left( {1 - {O_e}} \right)O_r^\prime \left( {{P_r}, \gamma } \right) $ | (18) |
2) 协作链路中断概率.根据2.2节中分析的协作链路发生中断的条件,得到协作链路的中断概率为
| $ \begin{array}{*{20}{c}} {{O_{c, {\rm{BRS}}}} = {O_d}\left( {{P_s}, \gamma } \right){O_e} + }\\ {{O_d}\left( {{P_s}, \gamma } \right)\left( {1 - {O_e}} \right)O_r^\prime \left( {{P_r}, \gamma } \right)} \end{array} $ | (19) |
下面给出中断性能的仿真与数值结果,并给出合理的解释说明.设置Monte Carlo仿真次数为10万次.除非另有说明,假设路径损耗指数为α= 4,其对应于城市蜂窝网络环境.传输时隙T=1 s,能量采集效率设定为η=0.6,源节点的传输功率为Ps=20 dBm,目标SINR为γ=-15 dBm,源节点与其关联目的节点之间的距离为d1=15 m,中继区域的半径为d2=7 m.高斯白噪声功率为σ2=-40 dBm,“源-目的”节点对的分布密度为μt =0.001,中继节点的分布密度为μr=0.001,功率分割系数ρ=0.5,中继区域的最大圆心角表示为θ0=arccos
图 2所示为系统中断概率与源节点传输功率Ps之间的关系,并将直接链路与中继链路的中断性能进行了对比.可以看出,对于不同的传输功率,中断概率的仿真结果与理论分析结果是完全一致的;其次,当中继节点的密度μr较大时,直接链路与中继链路的曲线之间有一个交叉点,对于较小的Ps,直接链路的性能优于中继链路;反之,则中继链路的性能优于直接链路.这是因为传输功率Ps的值直接影响到满足条件的中继节点的平均数目,进而影响中继链路的中断性能.最后,对于最优中继选择策略来说,增大Ps会增加选择到最优中继节点的概率,因此,最优中继选择策略下的中断性能要好于随机中继选择策略.
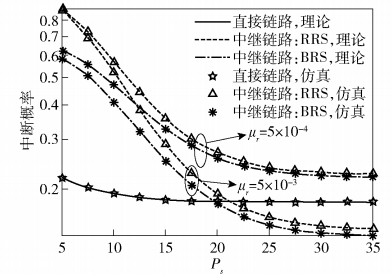
|
图 2 直接链路和中继链路中断概率与Ps之间的关系 |
图 3给出了在不同μt下系统中断概率与Ps之间的关系,并将直接链路与协作链路的中断性能进行了对比.从图中可以看出,对于不同的传输功率,中断概率的仿真结果与理论分析结果是完全一致的.其次,随着Ps的不断增大至Ps→∞,中断概率收敛于一个固定值.这是因为随着Ps的增大,系统成为干扰受限系统.另外,中断概率随着μt的增加而增大,这说明源节点密度增加造成的干扰对接收机的SINR有着不可忽略的影响.最后,当μt=3×10-3,Ps=35 dBm时,性能最优的BRS策略下的协作链路中断性能要比直接链路提升69.8%.
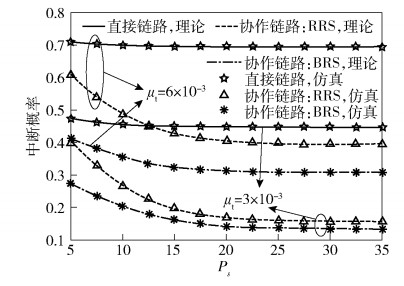
|
图 3 不同μt下中断概率与Ps之间的关系 |
图 4给出了不同γ下,基于RRS与BRS的协作链路中断概率与中继区域半径d2之间的关系.可以看出,中断概率首先随着d2的增加而减小,随后又逐渐增大.这是因为随着d2的增加,中继区域内中继节点非空的概率增大,从而目的节点享有协作分集的概率增大,因此,中断概率下降;然而,当d2的值继续增大超过一定的值时,在中继区域内选择距离源节点较远的中继节点的概率增加,由于路径损耗较大,中继节点收到的能量和接收信号强度均下降,进而目的节点接收到的信号强度较差,因此,中断概率增大.另外,中断概率随着γ的减小而降低,与图中结果保持一致.
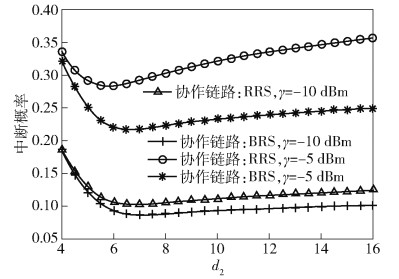
|
图 4 不同γ下协作链路中断概率与d2之间的关系 |
提出了一个大规模无线协作网络中的两阶段中继协作传输协议,以提升网络性能.在第1阶段,能够对源节点信号进行解码,并且位于其中继区域的中继节点成为潜在中继,协助源节点到目的节点的信息传输.在第2阶段,考虑两种不同的中继选择策略,首先分析直接链路的中断概率,然后将其分别与中继链路,以及协作链路的中断性能进行对比.理论和仿真结果表明,BRS方案下的协作链路的中断性能比直接链路提升了69.8%.
| [1] |
Chen Z, Cai L X, Cheng Y, et al. Sustainable cooperative communication in wireless powered networks with energy harvesting relay[J]. IEEE Transcations on Wireless Communications, 2017, 16(12): 8175-8188. DOI:10.1109/TWC.2017.2758365 |
| [2] |
Lu X, Wang P, Niyato D, et al. Wireless networks with RF energy harvesting:A contemporary survey[J]. IEEE Communications Surveys and Tutorials, 2014, 17(2): 757-789. |
| [3] |
Varshney L R. Transporting information and energy simultaneously[C]//Proc IEEE International Symposium on Information Theory, Toronto: [s. n.], 2008: 1612-1616.
|
| [4] |
Zhou X, Zhang R, Ho C K. Wireless information and power transfer:architecture design and rate-energy tradeoff[J]. IEEE Transcations on Communications, 2013, 61(11): 4754-4767. DOI:10.1109/TCOMM.2013.13.120855 |
| [5] |
Nasir A A, Zhou X, Durrani S, et al. Relaying protocols for wireless energy harvesting and information processing[J]. IEEE Transcations on Wireless Communications, 2013, 12(7): 3622-3636. DOI:10.1109/TWC.2013.062413.122042 |
| [6] |
Liu Y, Wang X. Information and energy cooperation in OFDM relaying[C]//Proc of IEEE International Conference on Communications (ICC). London: [s. n.], 2015: 5088-5098.
|
| [7] |
Stoyan D, Kendall W, Mecke J. Stochastic geometry and its applications[M]. [S. l.]: John Wiley and Sons, 1995.
|
| [8] |
Huang K. Spatial throughput of mobile ad hoc networks powered by energy harvesting[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7597-7612. DOI:10.1109/TIT.2013.2276811 |
| [9] |
Lee S, Zhang R, Huang K. Opportunistic wireless energy harvesting in cognitive radio networks[J]. IEEE Transcations on Wireless Communications, 2013, 12(9): 4788-4799. DOI:10.1109/TWC.2013.072613.130323 |
| [10] |
Krikidis I. Simultaneous information and energy transfer in large-scale networks with/without relaying[J]. IEEE Transcations on Communications, 2014, 62(3): 900-912. DOI:10.1109/TCOMM.2014.020914.130825 |
| [11] |
Haenggi M. Stochastic geometry for wireless networks[M]. [S. l.]: Cambridge University Press, 2012.
|
| [12] |
Lou Y, Yue Q, Cheng J, et al. Exact BER analysis of selection combining for differential SWIPT relaying systems[J]. IEEE Signal Processing Letters, 2017, 24(8): 1198-1202. DOI:10.1109/LSP.2017.2705066 |


