2. 山东理工大学 交通与车辆工程学院, 山东 淄博 255000
为探明减振器双向比对人-椅系统冲击动力学行为的影响规律,基于台架试验将座椅减振器阻尼特性简化为非对称分段线性函数,进而创建了人-椅非线性动力学模型及方程,并通过座椅台架试验验证了其有效性.以典型脉冲输入模拟座椅受到的垂向冲击,对不同强度脉冲激励工况、不同减振器双向比情况下的人-椅冲击动力学行为进行数值仿真.结果表明,当座椅减振器双向比大于1时,更有利于衰减驾驶室地板传递到驾乘人员的冲击;而且冲击输入强度越大,座椅减振器双向比大于1时的相对隔振效果越好.
2. School of Transportation and Vehicle Engineering, Shandong University of Technology, Shandong Zibo 255000, China
To ascertain the damper bidirectional ratio effect on the impact dynamic behavior of the human-seat system, the most widely used X-type seat is taken as the research object. Based on the measured data by the damper bench, the damper damping characteristic of the seat is simplified as an asymmetric piecewise linear function. A nonlinear dynamic model for the human-seat was proposed and its equation was created and validated by seat test. Based on the model and the equation, taking a typical pulse with different intensity as inputs, numerical simulations were carried out under different bidirectional ratios. It is shown that when the seat damper bidirectional ratio is larger than 1, it becomes more conducive to attenuate the impact on drivers, and the greater the impact input intensity is, the better the relative isolation effect is.
座椅系统作为物流车辆的最后一个隔振环节,决定着驾乘人员的舒适性,影响着驾乘人员的身体健康.人体医学研究表明,长时间地处于振动和冲击环境中,对人体健康的损害是非常严重的[1].近年来,由于振动造成的坐骨神经痛、腰痛、颈椎病及消化系统疾病等,已成为车辆驾驶人员常患的驾驶疾病;同时,振动导致的驾驶疲劳所引发的交通事故,正在慢慢侵蚀着人们的生命[2-3].
为了有效地衰减路面传递到人体的振动和冲击,车辆底盘悬架系统和座椅悬置系统一般均配置有减振器.准确地设计减振器的阻尼特性是提高乘坐舒适性的重要且有效手段之一[4].在底盘悬架系统中,非对称的非线性阻尼减振器应用广泛,其等效复原阻尼系数与压缩阻尼系数的比值称为减振器双向比.目前,对于座椅悬置减振器阻尼特性的设计,一般是直接借用底盘悬架减振器双向比的设计方法[5-6],但是座椅悬置系统与底盘悬架系统在结构和性能等方面存在较大差异[7],底盘悬架减振器双向比的设计方法并不完全适合座椅减振器设计.尽管国内外学者对底盘悬架减振器双向比开展了大量富有成效的研究,典型成果如Rajalingham等[8]研究了车辆底盘悬架减振器双向比对车辆振动响应的影响,Silveira等[9-10]利用底盘悬架非对称减振器提高乘用车、轿车的舒适性,但很少有文献系统地分析冲击工况下座椅减振器双向比对人-椅动力学行为的影响规律.为给座椅减振器阻尼特性的设计提供理论指导,建立一个能较真实地反映人-椅系统基本力学特征的动力学模型,进一步深入研究座椅减振器双向比对人-椅系统冲击动力学行为的影响规律,显得十分必要.
笔者以典型的商业化剪式座椅为研究对象,建立人-椅非线性动力学模型并进行试验验证,进而探究座椅系统在典型脉冲激励下,减振器双向比对人-椅系统冲击动力学响应的影响.
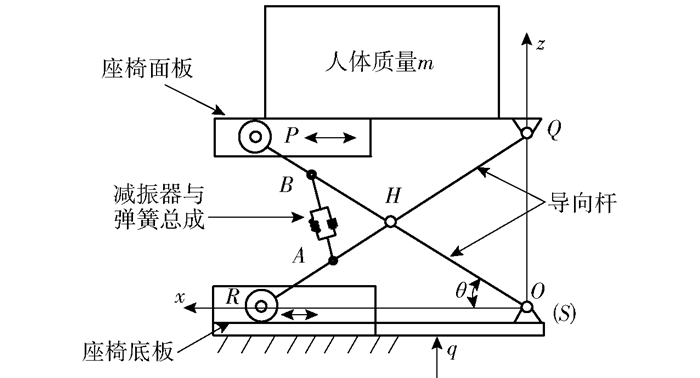
1 人-椅系统模型通常在满足分析需求的情况下,人体模型力求简单,以便于规律探讨.以应用最为广泛的剪式座椅作为研究对象,把人体视为有效质量为m的刚体,将人-椅系统简化为如图 1所示模型[11].
|
图 1 人-椅系统示意图 |
模型假设不计座椅悬置及导向机构的质量,不考虑它们的惯性及导向机构间摩擦.
除去座椅底板以外的运动构件有座椅面板、2个导向杆、减振器杆、减振器筒、2个导向轮,共7个运动构件;运动副包括:减振器杆、减振器筒之间1个移动副,减振器端部2个旋转副,P处导向轮与座椅面板之间1个移动副,R处导向轮与座椅导轨之间1个移动副,2个导向杆端部的4个旋转副,2个导向杆中间H处的1个旋转副,共10个低副.
人-椅系统的自由度为:7×3-10×2=1个.
设整体坐标系O-xyz的原点与座椅系统静平衡时导向杆与导轨的铰接点S重合,x轴水平向前,z轴垂直向上.设PS=QR=L,AR=a,BS=b,BP=c,AB=l0.在外界激励q作用下,导致导向杆PS绕着y轴旋转了角度φ.座椅静平衡时φ为零.由于该系统具有1个自由度,故可选取φ为广义坐标.
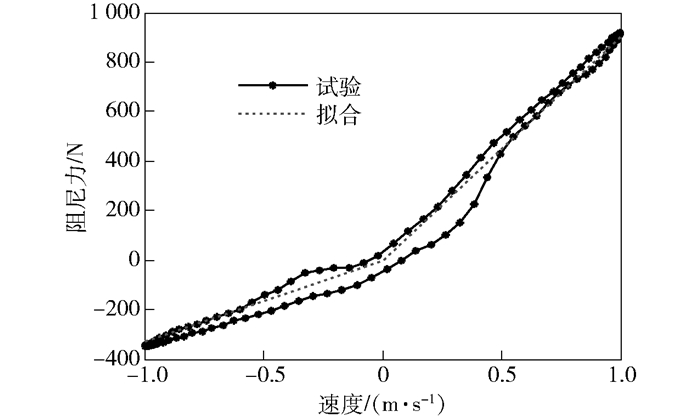
2 人-椅系统振动方程及试验验证 2.1 人-椅系统振动方程为了便于理论分析以探明规律,可基于减振器台架试验数据建立减振器速度-阻尼力简化模型.根据QC/T 545—1999[12],利用长春试验机有限公司生产的30 kN综合试验台,对某物流车剪式座椅系统减振器进行了台架试验,如图 2所示.所得减振器速度v-阻尼力Fc特性曲线,如图 3所示.

|
图 2 座椅减振器台架试验 |
|
图 3 座椅减振器速度-阻尼力特性曲线 |
由图 3可知,当减振器相对运动速度v>0和v<0时,试验曲线可近似为斜率为βCa和Ca的2条直线,分别对应复原速度-阻尼力曲线和压缩速度-阻尼力曲线,其中,β为座椅减振器双向比.设座椅减振器对称阻尼特性曲线的阻尼系数为C0,则根据减振器一个工作行程内消耗能量守恒,可得
| $ \beta C_{\mathrm{a}}+C_{\mathrm{a}}=2 C_{0} $ | (1) |
根据式(1)并结合人-椅系统模型,可将座椅减振器阻尼系数C表示为
| $ C=\left\{\begin{array}{l}{\frac{2 \beta C_{0}}{\beta+1}\left[(a-c)^{2}-(a-b)^{2}\right] \dot{\varphi} \sin (2 \theta-2 \varphi) \geqslant 0} \\ {\frac{2 C_{0}}{\beta+1}\left[(a-c)^{2}-(a-b)^{2}\right] \dot{\varphi} \sin (2 \theta-2 \varphi)<0}\end{array}\right. $ | (2) |
人-椅系统的拉格朗日方程形式为
| $ \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial T}{\partial \dot{\varphi}}\right)-\frac{\partial T}{\partial \varphi}+\frac{\partial V}{\partial \varphi}+\frac{\partial D}{\partial \dot{\varphi}}=0 $ | (3) |
其中T、D及V分别为人-椅系统的动能、势能及耗散能.
式(3)可进一步表示为
| $ \begin{array}{c}{m\left[\ddot{q}-\ddot{\varphi} L \cos (\theta-\varphi)-\dot{\varphi}^{2} L \sin (\theta-\varphi)\right] \times} \\ {[-L \cos (\theta-\varphi)]+K\left\{\left[(a-c)^{2} \cos ^{2}(\theta-\varphi)+\right.\right.} \\ {(a-b)^{2} \sin ^{2}(\theta-\varphi) ]^{1 / 2}-l_{0} \} \times} \\ {\left[(a-c)^{2} \cos ^{2}(\theta-\varphi)+(a-b)^{2} \sin ^{2}(\theta-\varphi)\right]^{-1 / 2} \times} \\ {0.5\left[(a-c)^{2} \sin (2 \theta-2 \varphi)-(a-b)^{2} \sin (\theta-\varphi)\right]+} \\ {\quad \frac{C\left[(a-c)^{2}-(a-b)^{2}\right]^{2} \dot{\varphi} \sin ^{2}(2 \theta-2 \varphi)}{4\left[(a-c)^{2} \cos ^{2}(\theta-\varphi)+(a-b)^{2} \sin ^{2}(\theta-\varphi)\right]}=0}\end{array} $ | (4) |
为了验证所建人-椅系统模型及方程的有效性,对某物流车剪式座椅系统进行了试验和仿真对比.其中,所研究座椅系统的参数为:L=375 mm,a=72 mm,c=21 mm,弹簧刚度K=24.5 kN/m,C0=950 Ns/m,m=55 kg,系统固有频率f0=2.4 Hz.
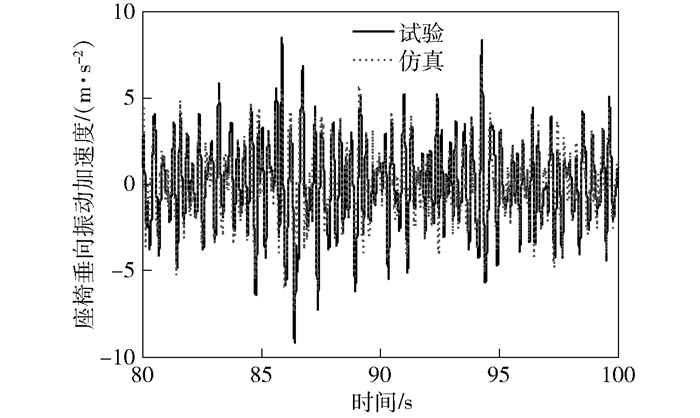
将座椅安装在座椅振动试验台上,用60 kg的配重块代替驾驶员.通过试验台对座椅施加时间长度为120 s的白噪声随机激励信号,并利用PCB 356A26型加速度计测取座椅面垂向振动加速度信号.以相同的随机激励信号作为所建人-椅系统模型的输入,根据座椅系统参数对座椅动力学响应进行数值仿真,仿真时间长度为120 s. 图 4为仿真结果与试验结果对比.为了清晰地考察仿真与试验结果的差异,将时间显示范围设置为80~100 s.分析图 4可知,座椅面垂向振动加速度ap的时间历程试验曲线和仿真曲线吻合较好.对比结果表明,所建人-椅动力学模型是有效的.
|
图 4 座椅振动试验及仿真结果对比 |
为给座椅减振器设计提供指导,将复原阻尼与压缩阻尼的比值关系分为3类,即β=3、β=1/3及β=1,进而对人-椅动力学响应进行模拟和评价.为了分析减振器双向比对人-椅冲击动力学响应的影响规律,选择典型的脉冲输入模拟座椅在驾驶室地板上安装位置处的垂向冲击,即
| $ q(t)=\frac{73 \gamma^{2} f_{0}^{2} t^{2} q_{\mathrm{m}}}{\mathrm{e}^{2 \pi \gamma f_{0} i}} $ | (5) |
其中:qm为脉冲输入位移幅值;γ为振动剧烈因子.
由式(5)可知,振动剧烈因子γ越大,瞬间冲击越剧烈.这里,取qm=30 mm.利用γ=6情况下的脉冲输入模拟驾驶室地板对座椅较强的冲击;利用γ=2情况下的脉冲输入模拟驾驶室地板对座椅很弱的冲击. Zhao等[11]仅分析了人体振动加速度ap时域响应及动能T的变化规律.为进一步深入考察减振器双向比的影响规律,重点分析人体振动加速度ap的功率谱密度PSD、座椅悬置动挠度fd=zp-q及系统耗散能D响应.
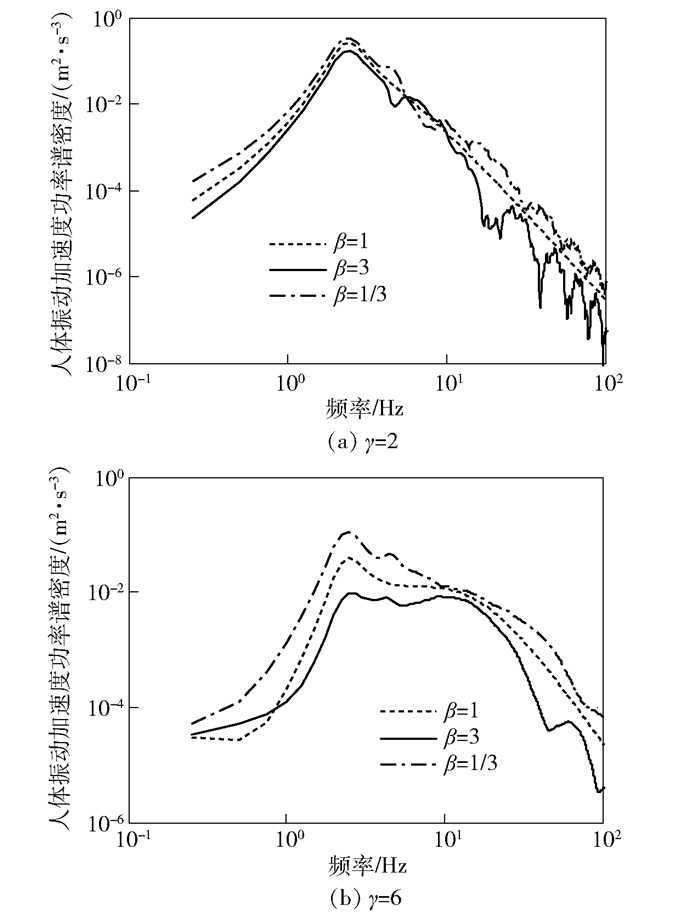
3.1 对加速度功率谱密度的影响γ=2和γ=6情况下,不同减振器双向比β取值时的人体振动加速度功率谱密度PSD曲线,如图 5所示.
|
图 5 人体振动加速度功率谱密度曲线对比 |
分析图 5(a)可知,人-椅系统在较弱的脉冲激励时(γ=2),双向比β=3情况下的人体振动加速度功率谱密度曲线几乎在其他2种情况之下;仅在4.0~7.0 Hz中频区,PSD值略大于其他2种情况.对比结果表明,人-椅系统在较弱的脉冲激励时,与其他两种情况相比,β=3情况下座椅的整体隔振效果较好.分析图 5(b)可知,人-椅系统在较强的脉冲激励时(γ=6),双向比β=3情况下,在整个频域内的PSD值几乎均低于其他2种情况,仅在0.8 Hz以下的低频区略大于β=1的情况,但PSD值均很小,对人体振动影响不大.对比结果表明,人-椅系统在较强的脉冲激励时,β大于1情况下有利于衰减人-椅系统的振动.
对比图 5(a)和图 5(b)还可发现,在共振区,γ=2情况下的PSD略高于γ=6情况下的PSD;但在10.0 Hz左右的区域,γ=6情况下的PSD明显高于γ=2情况下的PSD.对比结果表明,人-椅系统在不同激振强度下,人体的振动能量在频域内的分布是不同的,且随着激振强度的增大,人体振动能量向更高的频率转移.
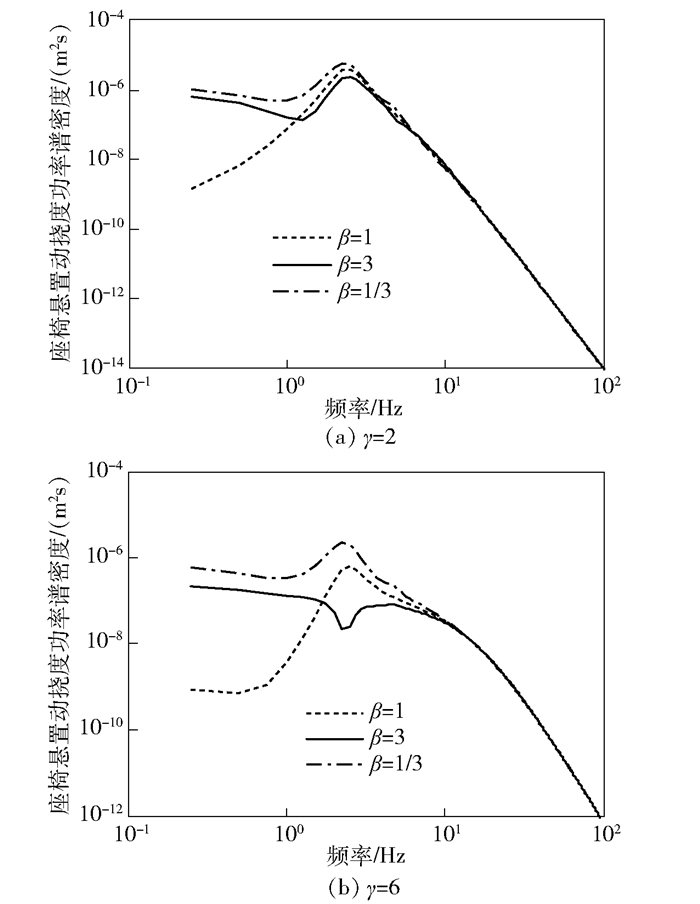
3.2 对座椅悬置动挠度响应的影响γ=2和γ=6情况下,不同减振器双向比β取值时的座椅悬置动挠度功率谱密度PSD曲线,分别如图 6所示. γ=2和γ=6情况下,不同减振器双向比β取值时的座椅悬置动挠度时间历程曲线如图 7所示.
|
图 6 座椅悬置动挠度功率谱密度曲线对比 |
|
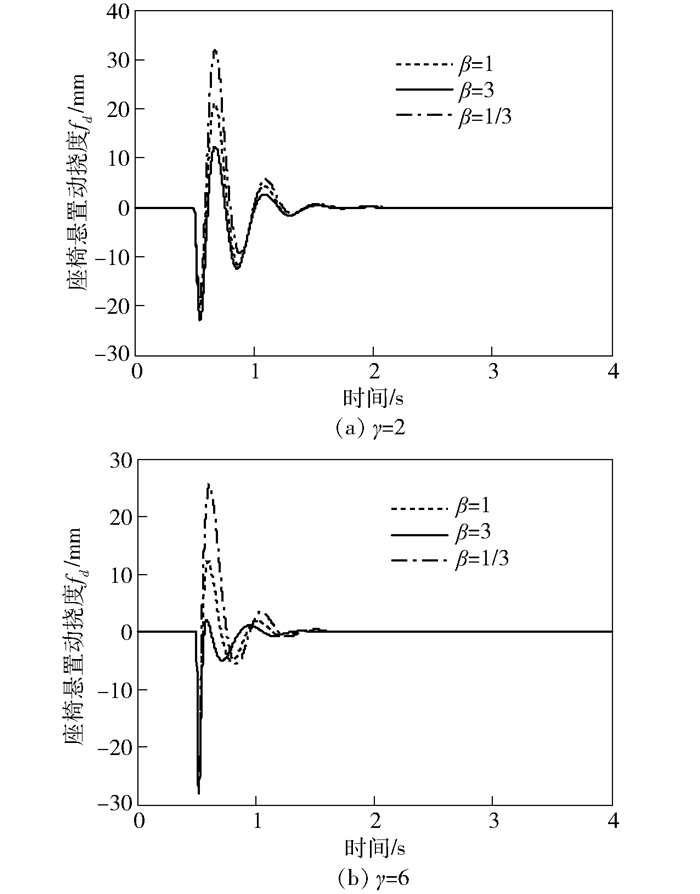
图 7 座椅悬置动挠度时间历程对比 |
分析图 6(a)可知,人-椅系统在较弱的脉冲激励时(γ=2),双向比β=3情况下的座椅悬置动挠度功率谱密度PSD值在共振区小于其他两种情况,但在约1.0 Hz以下的低频区处于其他两种情况之间;在高频区域,3种减振器双向比β取值情况下的座椅悬置动挠度功率谱密度PSD值无明显差别. 图 6(b)表明,人-椅系统在较强的脉冲激励时(γ=6),减振器双向比β=对座椅悬置动挠度功率谱密度PSD的影响规律类似,但也存在一定的差异.与γ=2情况相比,γ=6情况下的PSD在10.0 Hz处出现明显的“上凸”现象,这一现象与图 5(b)所示的人体振动加速度功率谱密度曲线类似.对比结果表明,人-椅系统配置复原阻尼大于压缩阻尼的减振器(β>1),也有助于减小冲击激励下的座椅悬置动挠度响应.
图 7(a)表明,人-椅系统在较弱的脉冲激励时(γ=2),与β=1情况相比,在β=1/3情况下座椅悬置动挠度fd发生了“上移”现象;在β=3情况下,发生了“下压”现象.由此可知,“上移”现象使得人体振动的幅值及平均位置向上移动;“下压”现象使得人体振动的幅值及平均位置向下移动.从驾驶员便于操纵方向盘及仪表盘的角度来看,严重的“上移”和“下压”现象是不利的.在频繁的脉冲激励下,除了振动对人体产生冲击伤害之外,“上移”和“下压”现象也会迫使驾驶员频繁地改变视线并调整驾驶姿态,在一定程度上造成了视觉疲劳,进一步加剧驾驶疲劳.因此,在实际工程中,虽然β>1情况下减振器有助于衰减人-椅系统冲击振动,但β值不宜过大.由图 7(b)可知,人-椅系统在较强的脉冲激励时(γ=6),在β=3情况下,虽然在第1个压缩行程开始,相对动挠度fd最大,但从第一个复原行程开始,相对位移小于其他两种情况,这种现象的发生是由减振器非对称阻尼特性决定的.对于β=3情况,由于压缩行程阻尼力较小,故发生较大的相对位移,但是由于复原阻尼较大,可有效抑制座椅的复原位移,故从第一个复原行程开始相对位移小于其他两种情况下的相对位移.
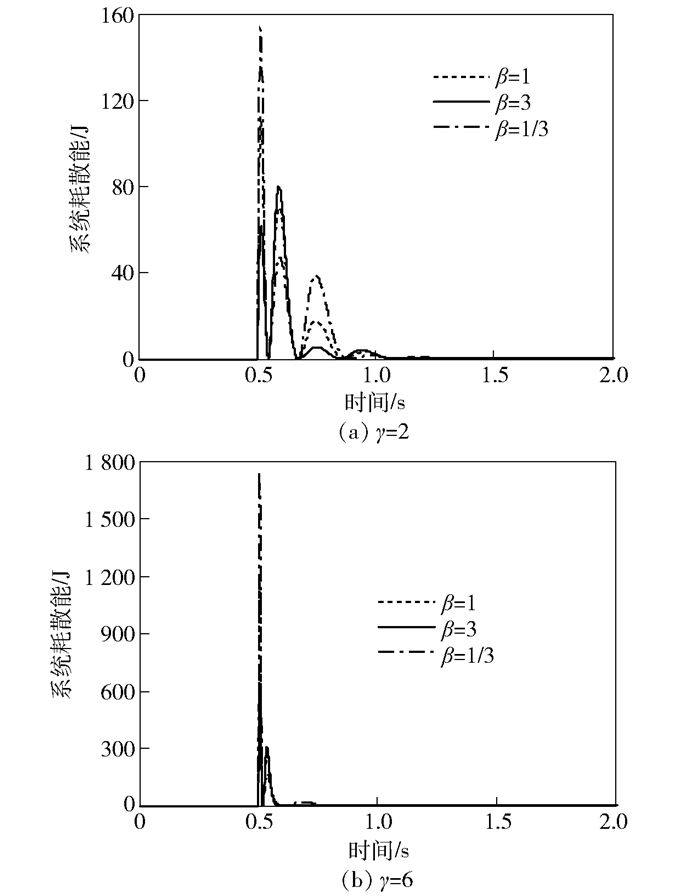
3.3 对系统耗散能的影响γ=2和γ=6情况下,不同减振器双向比β取值时的人-椅系统耗散能时间历程曲线如图 8所示.
|
图 8 系统耗散能时间历程对比 |
由图 8(a)可知,β=3情况与β=1和β=1/3两种情况相比,冲击输入下系统能量的平均耗散效果较好,这说明人-椅系统配置复原阻尼大于压缩阻尼的减振器,有助于衰减驾驶室地板传递到人体的能量,从而有助于提高舒适性. 图 8(b)说明,与较弱的脉冲激励下相比,在较强的脉冲激励下,β=3情况下耗散传递到人体振动能量的效果更加明显.结果表明,在较强的脉冲激励下,人-椅系统配置复原阻尼大于压缩阻尼的减振器,更有助于衰减驾驶室地板传递到座椅的振动能量.此外,β>1情况下,系统耗散能D的最大值明显小于其他2种情况,人-椅系统配置复原阻尼大于压缩阻尼的减振器有利于减小减振器的工作负荷,延长减振器的使用寿命.
4 结束语以应用广泛的剪式座椅为研究对象,建立了人-椅系统的动力学模型及方程,并验证了其有效性.选取典型的脉冲为输入,对座椅减振器不同双向比β取值下的人-椅动力学行为进行了数值模拟和对比分析.结果表明:人-椅系统在较弱的脉冲激励时,与β=1情况相比,β < 1情况下座椅悬置动挠度fd发生了“上移”现象;β>1情况下,发生了“下压”现象;在较强的脉冲激励下,人-椅系统配置复原阻尼大于压缩阻尼的减振器(β>1),更有助于衰减座椅的振动,也有助于延长减振器使用寿命;在实际工程中,β值不宜过大;人-椅系统在不同激振强度下,人体的振动能量在频域内的分布不同,且随着激振强度的增大,人体振动能量向更高的频率转移.本文所探明的冲击工况下座椅减振器双向比对座椅驾乘舒适性及动力学行为的影响规律,可为座椅减振器阻尼特性的设计提供有益参考.
| [1] |
Crizzle A M, Bigelow P, Adams D, et al. Health and wellness of long-haul truck and bus drivers:a systematic literature review and directions for future research[J]. Journal of Transport and Health, 2017, 7: 90-109. DOI:10.1016/j.jth.2017.05.359 |
| [2] |
Zhou Zhen, Griffin M J. Response of the seated human body to whole-body vertical vibration, discomfort caused by sinusoidal vibration[J]. Ergonomics, 2014, 57(5): 714-732. DOI:10.1080/00140139.2014.898799 |
| [3] |
Deboli R, Calvo A, Preti C. Whole-body vibration:measurement of horizontal and vertical transmissibility of an agricultural tractor seat[J]. International Journal of Industrial Ergonomics, 2017, 58: 69-78. DOI:10.1016/j.ergon.2017.02.002 |
| [4] |
周长城, 潘礼军, 于曰伟, 等. 车辆钢板弹簧悬架系统减振器最佳阻尼匹配[J]. 农业工程学报, 2016, 32(7): 106-113. Zhou Changcheng, Pan Lijun, Yu Yuewei, et al. Optimal damping matching for shock absorber of vehicle leaf spring suspension system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(7): 106-113. |
| [5] |
Tufano S, Griffin M J. Nonlinearity in the vertical transmissibility of seating:the role of the human driver apparent mass and seat dynamic stiffness[J]. Vehicle System Dynamics, 2013, 51(1): 122-138. DOI:10.1080/00423114.2012.715652 |
| [6] |
Ksiazek M A, Ziemianski D. Optimal driver seat suspension for a hybrid model of sitting human body[J]. Journal of Terramechanics, 2012, 49(5): 255-261. DOI:10.1016/j.jterra.2012.07.001 |
| [7] |
Zhao Leilei, Zhou Changcheng, Yu Yuewei, et al. Hybrid modelling and damping collaborative optimisation of five-suspensions for coupling driver-seat-cab system[J]. Vehicle System Dynamics, 2016, 54(5): 667-688. DOI:10.1080/00423114.2016.1151902 |
| [8] |
Rajalingham C, Rakheja S. Influence of suspension damper asymmetry on vehicle vibration response to ground excitation[J]. Journal of Sound and Vibration, 2003, 266(5): 1117-1129. DOI:10.1016/S0022-460X(03)00054-3 |
| [9] |
Silveira M, Jr Pontes B R, Balthazar J M. Use of nonlinear asymmetrical shock absorber to improve comfort on passenger vehicles[J]. Journal of Sound and Vibration, 2014, 333(7): 2114-2129. DOI:10.1016/j.jsv.2013.12.001 |
| [10] |
Silveira M, Wahi P, Fernandes J C M. Effects of asymmetrical damping on a 2 DOF quarter-car model under harmonic excitation[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 43: 14-24. DOI:10.1016/j.cnsns.2016.06.029 |
| [11] |
Zhao L L, Yang F X, Yu Y W, et al. Influence of shock absorber asymmetry on vibration responses of seat-occupant system under impact condition[C]//2017 International Conference on Modelling, Identification and Control(ICMIC 2017). New York: IEEE Press, 2017: 394-399.
|
| [12] |
长春汽车研究所. QC/T 545-1999.汽车筒式减振器台架试验方法[S]. 1999.
|


