大规模多输入多输出(MIMO，multiple input multiple output)技术被提出以后受到学术界与工业界的广泛关注，将成为第5代移动通信系统(5G, the fifth generation of mobile communications system)的关键技术^[1-4].随着天线规模的剧增，大规模MIMO系统信号检测面临新挑战.当天线数达到上百等级时，最大似然检测是不现实的，只能考虑次优的方法^[5].其中迫零(ZF，zero forcing)检测和线性最小均方误差(LMMSE，linear minimum mean square error)检测的运算复杂度较低，但效果也较次.串行干扰消除(SIC，successive interference cancellation)与线性最小均方误差结合会使LMMSE检测性能大幅度提高，但LMMSE-SIC需要执行多次矩阵求逆运算，对大规模天线阵列而言复杂度太高.基于树搜索的检测方法，如QRD-M在天线规模较大时，树的深度与树枝数目激增，其复杂度骤增，且性能下降.

期望传播(EP，expectation propagation)算法是一种随机变量后验概率边缘分布的近似计算方法，由Minka^[6]于2001年提出，已经在人工智能和机器学习领域得到广泛应用，在信号检测领域^[7]，也引起了不少学者的关注.笔者结合循环冗余校验，提出一种基于期望传播的自适应大规模MIMO信号检测方法，可显著降低EP迭代次数，从而降低算法运算复杂度，同时能保证检测性能基本不受影响.

1 系统模型及EP算法

假设系统中有N_t根发送天线和N_r根接收天线.用列向量$\boldsymbol{x}=\left(x_{1}, x_{2} \cdots, x_{N_{{\rm t}}}\right)^{\mathrm{T}} \in \mathbb{C}^{N_{\mathrm{t}} \times 1} $表示发送信号，其元素以独立等概方式取值于星座图S={Ω₁，Ω₂…, Ω_M}.令$\boldsymbol{H} \in \mathbb{C}^{N_{\mathrm{r}} \times N_{\mathrm{t}}} $表示MIMO信道矩阵，则接收信号为

$ \boldsymbol{y}=\boldsymbol{H} \boldsymbol{x}+\boldsymbol{w} $

(1)

其中$\boldsymbol{w} \in \mathbb{C}^{N_{\mathrm{r}} \times 1} $表示加性高斯白噪声，其元素是独立同分布的零均值循环对称复高斯随机变量，方差均为σ².假设接收端理想已知信道H和σ².

MIMO检测的任务是根据收到信号y来估计发送信号x.考虑使用贝叶斯估计方法，将后验均值作为估计值，则x_i, i=1, 2, …, N_t的估计值为

$ {\hat x_i} = \int {{x_i}} p\left( {{x_i}|\mathit{\boldsymbol{y}}} \right){\rm{d}}{x_i} $

(2)

其中p(x_i|y)是联合后验概率密度分布p(x|y)的边缘分布.根据贝叶斯公式

$ p(\boldsymbol{x} | \boldsymbol{y}) \propto p(\boldsymbol{y} | \boldsymbol{x}) p(\boldsymbol{x}) $

(3)

其中∝表示正比于，两者只相差一个系数. p(x)为向量x的先验概率密度函数：

$ p(\mathit{\boldsymbol{x}}) = \prod\limits_{i = 1}^{{N_{\rm{t}}}} {\left\{ {\frac{1}{M}\sum\limits_{m = 1}^M \delta \left( {{x_i} - {\mathit{\Omega }_m}} \right)} \right\}} $

(4)

p(y|x)为信道的转移概率密度函数：

$ p(\boldsymbol{y} | \boldsymbol{x}) \propto \mathrm{CN}\left(\boldsymbol{y} ; \boldsymbol{H} \boldsymbol{x}, \sigma^{2} \boldsymbol{I}\right) $

(5)

其中CN(y; Hx, σ²I)表示循环对称复高斯向量y的概率密度函数，其均值为Hx，协方差矩阵为σ²I.

为了求解式(2)，EP用高斯分布对后验概率密度分布做近似，且限定高斯分布的协方差矩阵为对角阵.首先用一个循环对称高斯分布替换先验概率密度分布p(x)，得到

$ q(\mathit{\boldsymbol{x}}|\mathit{\boldsymbol{\gamma }}, \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}) \propto {\rm{CN}}\left( {\mathit{\boldsymbol{y}};\mathit{\boldsymbol{Hx}}, {\sigma ^2}\mathit{\boldsymbol{I}}} \right){\rm{CN}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}\mathit{\boldsymbol{\gamma }}, {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}} \right) $

(6)

其中向量γ、对角阵Λ是函数q的参数.

由式(6)知q(x|γ, Λ)也服从循环对称复高斯分布，即

$ q(\mathit{\boldsymbol{x}}|\mathit{\boldsymbol{\gamma }}, \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}) \propto {\rm{CN}}(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\mu }}, \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) $

(7)

其中

$ \left. \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = {\left( {{\sigma ^{ - 2}}{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right)^{ - 1}}\\ \mathit{\boldsymbol{\mu }} = \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}\left( {{\sigma ^{ - 2}}{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{y}} + \mathit{\boldsymbol{\gamma }}} \right) \end{array} \right\} $

(8)

其中(·)^H表示共轭转置.

然后构造

$ {q_{{\rm{EP}}}}(\mathit{\boldsymbol{x}}|\mathit{\boldsymbol{\gamma }}, \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}) \propto {\rm{CN}}(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\mu }}, {\mathop{\rm diag}\nolimits} (\mathit{\boldsymbol{ \boldsymbol{\varSigma} }})) $

(9)

其中diag(Σ)表示只保留矩阵Σ的对角线元素所形成的对角阵.用q_EP(x|γ, Λ)作为目标后验概率密度p(x|y)的近似，其边缘分布为

$ \begin{array}{*{20}{c}} {{q_{{\rm{EP}}}}\left( {{x_i}} \right) \propto {\rm{CN}}\left( {{x_i};{\mu _i}, {\mathit{\Sigma }_i}} \right) = }\\ {{q^{\backslash i}}\left( {{x_i}} \right){\rm{CN}}\left( {{x_i};\frac{{{\gamma _i}}}{{{\mathit{\Lambda }_i}}}, \frac{1}{{{\mathit{\Lambda }_i}}}} \right)} \end{array} $

(10)

其中μ_i为μ的第i个元素，Σ_i为Σ对角线的第i个元素，γ_i为γ的第i个元素，Λ_i为Λ对角线的第i个元素，q^\i(x_i)∝CN(x_i; μ^\i, Σ^\i)也是一个高斯分布，其均值μ^\i和方差Σ^\i为

$ \left. {\begin{array}{*{20}{l}} {{\mathit{\Sigma }^{\backslash i}} = {{\left( {\frac{1}{{{\mathit{\Sigma }_i}}} - {\mathit{\Lambda }_i}} \right)}^{ - 1}}}\\ {{\mu ^{\backslash i}} = {\mathit{\Sigma }^{\backslash i}}\left( {\frac{{{\mu _i}}}{{{\mathit{\Sigma }_i}}} - {\gamma _i}} \right)} \end{array}} \right\} $

(11)

构造概率密度函数h(x_i)∝q^\i(x_i)p(x_i)，i=1, 2, …, N_t，其中p(x_i)为p(x)的边缘分布，然后计算

$ \left. {\begin{array}{*{20}{l}} {\mu _i^\prime = {E_{h\left( {{x_i}} \right)}}\left\{ {{x_i}} \right\} = \int {{x_i}} h\left( {{x_i}} \right){\rm{d}}{x_i}}\\ {\mathit{\Sigma }_i^\prime = {E_{h\left( {{x_i}} \right)}}\left\{ {{{\left| {{x_i} - \mu _i^\prime } \right|}^2}} \right\} = \int {{{\left| {{x_i} - \mu _i^\prime } \right|}^2}} h\left( {{x_i}} \right){\rm{d}}{x_i}} \end{array}} \right\} $

(12)

将以上数字特征传递给q_EP(x_i)，使得

$ \left. {\begin{array}{*{20}{l}} {{E_{{q_{{\rm{EP}}}}\left( {{x_i}} \right)}}\left\{ {{x_i}} \right\} = {E_{h\left( {{x_i}} \right)}}\left\{ {{x_i}} \right\} = \mu _i^\prime }\\ {{E_{{q_{{\rm{EP}}}}\left( {{x_i}} \right)}}\left\{ {{{\left| {{x_i} - \mu _i^\prime } \right|}^2}} \right\} = {E_{h\left( {{x_i}} \right)}}\left\{ {{{\left| {{x_i} - \mu _i^\prime } \right|}^2}} \right\} = \mathit{\Sigma }_i^\prime } \end{array}} \right\} $

(13)

因此有CN(x_i; μ′_i, Σ′_i)∝CN(x_i; μ^\i, Σ^\i) CN(x_i; γ_i^new/Λ_i^new, 1/Λ_i^new)，从而把γ_i与Λ_i修正为γ_i^new=$ \frac{{\mu _i^\prime }}{{\mathit{\Sigma }_i^\prime }} - \frac{{{\mu ^{\backslash i}}}}{{{\mathit{\Sigma }^{\backslash i}}}}$与$\mathit{\Lambda }_i^{{\rm{new}}} = \frac{1}{{\mathit{\Sigma }_i^\prime }} - \frac{1}{{{\mathit{\Sigma }^{\backslash i}}}}, i = 1, 2 \cdots , {N_{\rm{t}}} $.为了使迭代更稳定，加入线性滤波：

$ \left. {\begin{array}{*{20}{l}} {\mathit{\Lambda }_i^{{\rm{new}}} = \alpha {\mathit{\Lambda }_i} + (1 - \alpha )\left( {\frac{1}{{\mathit{\Sigma }_i^\prime }} - \frac{1}{{{\mathit{\Sigma }^{1i}}}}} \right)}\\ {\gamma _i^{{\rm{new}}} = \alpha {\gamma _i} + (1 - \alpha )\left( {\frac{{\mu _i^\prime }}{{\mathit{\Sigma }_i^\prime }} - \frac{{{\mu ^{\backslash i}}}}{{{\mathit{\Sigma }^{\backslash i}}}}} \right)} \end{array}} \right\} $

(14)

其中α为介于0和1之间的阻尼系数.

给定γ与Λ的初始值，当γ与Λ迭代收敛或迭代结束后，后验均值$\mathit{\boldsymbol{\hat x}} $的估计值取为μ.

2 自适应EP算法

在EP算法中，参数更新过程的计算复杂度主要取决于式(8)中计算矩阵Σ所需的求逆，其复杂度为O(LN_t³)数量级，其中L为迭代次数.对于大规模MIMO天线阵列而言，发送天线数N_t可达上百的等级，因此减少式(8)中矩阵求逆的次数对减少设备能耗及复杂度有非常重要的意义.

EP算法中的迭代次数L越大，检测性能也越好.在实际当中可以观察到，对于不同的输入信号样本y，其达到检测正确所需要的迭代次数并不相同.基于此，参考Turbo、LDPC码中普遍采用的做法^[8-9], 可以考虑在发现检测正确后停止继续迭代.识别检测正确的方法可以有很多，简单起见笔者考虑使用循环冗余校验码(CRC，cyclic redundancy check)，如图 1所示.虽然CRC校验比特会带来一些开销，但对于大规模天线系统来说，加入少量CRC比特是可以接受的. 图 2示出了所提自适应EP算法的流程图.

3 仿真结果

下面通过仿真来验证所提的自适应EP算法，仿真中采用QPSK调制.考虑瑞利信道，H的元素是独立同分布的零均值复高斯，方差为1.一般要求接收天线数目不小于发送天线数目，且当接收天线数目远大于发送天线数目时，线性检测即可获得良好效果^[10]，因此考虑天线配置N_r=160，N_t=128以及N_r=N_t=256两种情形.仿真中还考虑了LMMSE、LMMSE-SIC以及QRD-M三种常见的经典检测方法作为对比.

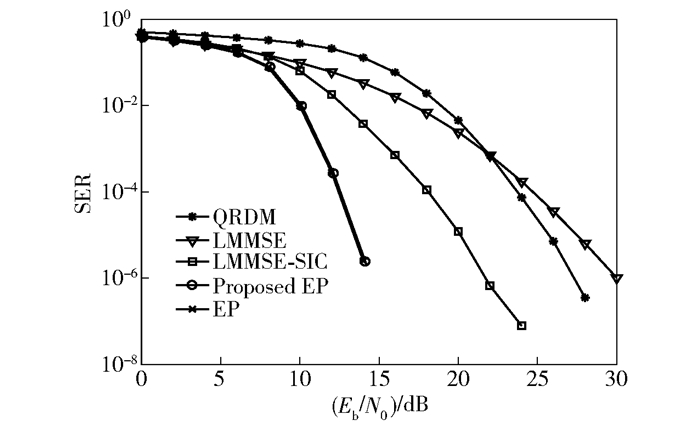
图 3与图 4分别是160×128、256×256两种天线配置下的误符号率(SER，symbol error rate)性能.仿真中，QRD-M算法中每层的保留分支数M设为20，EP的阻尼系数设为α=0.9.图中“EP”表示固定迭代次数L=5的EP检测算法，“Proposed EP”表示最大迭代次数为L_max=5的自适应EP检测算法.采用自适应EP检测算法时，发送端在比特序列中插入了16位CRC校验位.对160×128配置，净信息比特数是128×2-16=240 bit，对于256×256配置，净信息比特数是256×2-16=496 bit.图中E_b/N₀已经考虑了CRC比特的开销.可以看到，无论是EP还是自适应EP，其SER性能都显著优于LMMSE、LMMSE-SIC和QRD-M算法.在同等SER下，自适应EP比EP略差，这个性能损失由CRC校检位开销带来.对于160×128配置，E_b/N₀相差10lg(256/240)≈0.28 dB.对于256×256配置，E_b/N₀相差10lg(512/496)≈0.13 dB. 图 3、图 4的结果与此一致.

在计算复杂度方面，LMMSE只需要做1次矩阵求逆操作，复杂度为O(N_t³)数量级. LMMSE-SIC需要做N_t次矩阵求逆，每次求逆的矩阵维度递次减小，复杂度为$ O\left( {\sum\limits_{i = 2}^{{N_{\rm{t}}}} {{i^3}} } \right)$数量级，发送天线数N_t较大时，大致是$ O\left(\frac{1}{4} N_{\mathrm{t}}^{4}\right)$. EP算法的复杂度为O(LN_t³)的数量级，其中L为迭代次数.自适应EP算法的复杂度为O(LN_t³)的数量级，其中L为平均迭代次数.仿真中，天线配置为N_t=128及256，而EP的迭代次数是5，所以EP的复杂度远低于LMMSE-SIC. QRD-M算法需要做1次矩阵QR分解，然后逐层减枝，在大规模天线下计算复杂度较高且不容易直接衡量^[11].从仿真运行时间来看，在相同平台(Matlab R2014a，CPU为i7-4770，8 GB内存)、相同仿真条件(天线配置160×128、信噪比14 dB，收发10万次)下，QRD-M算法平均每次实验的运行时间为0.144 93 s，而EP仅需0.040 53 s，EP的复杂度低于QRD-M. 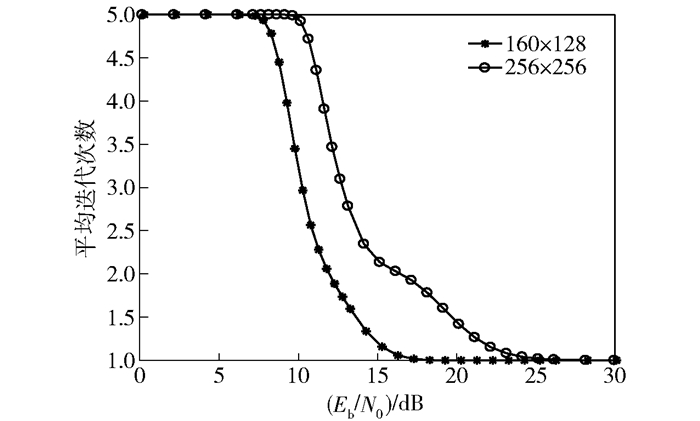图 5示出了最大迭代次数L_max=5的基于EP的自适应检测算法在各E_b/N₀条件下的平均迭代次数.随着E_b/N₀的增加，EP算法中的迭代收敛速度加快，特别是在高信噪比情况下，自适应EP的平均迭代次数近似为1次，与LMMSE相当.但其SER性能显著优于LMMSE.

4 结束语

考虑到器件的功耗，大规模MIMO下信号检测必须兼顾运算复杂度与性能.笔者提出一种基于EP的自适应大规模MIMO信号检测算法，结合CRC校验降低EP迭代次数，从而减少高维矩阵求逆的次数，降低算法运算复杂度并保证检测性能.