无线携能通信(SWIPT, simultaneous wireless information and power transfer)技术是解决能源消耗的关键技术之一，其主要目的是从信息传输的射频(RF, radio frequency)信号中获取所需能量^[1].在协作系统下应用SWIPT技术，可以给中继端提供能量，从而降低能耗.在SWIPT和协作的背景下，在无线携能协作中继处使用空间调制(SM)技术，从而提高了系统的性能^[2]. SM是在传统调制符号的基础上通过激活不同发射天线的索引值来携带额外的比特，SM明显的缺点是频谱效率相比多输入多输出(MIMO, multiple input multiple output)系统要低，与发射天线数仅呈对数关系.若要提高频谱效率，广义空间调制(GSM, generalized spatial modulation)^[3]是其中有吸引力的方案之一. GSM每一时隙可以激活多根发射天线，实现了增强的频谱效率，同时保持了SM的主要优点，但GSM系统在静态衰落环境下存在着严重的干扰.而基于媒介的索引调制(MBM, media based modulation)^[4]利用内在的分集能很好地对抗静态衰落.媒介调制的核心思想是将发送信息包含在RF镜开关状态中，即利用RF镜的不同状态构造出不同信道模型来发送不同消息，在提高频谱利用率、节省能耗和克服干扰上具有很大优势.

基于上述背景，提出了广义空间媒介调制(GSM-MBM)的无线携能协作通信系统.该系统在中继处使用GSM-MBM^[5]技术替代传统的SM、单输入多输出媒介索引调制(SIMO-MBM, single input multiple output-media based modulation)和基于媒介空间调制(SM-MBM, spatial modulation-media based modulation)技术^[6]，从而提高了信息的传输效率，解决了频谱效率低的问题，同时，误码率性能、抗干扰性和能耗也得到了明显改善.

1 GSM-MBM无线携能协作系统

GSM-MBM无线携能协作系统如图 1所示，信源具有N_S根发射天线、中继具有N_T根天线，目的节点具有N_R根天线.传输过程包括2个阶段.第1阶段是S-R链路.在中继接收端，根据SWIPT技术的功率切割(PS, power splitting)协议，将接收的信号分为两部分，$\sqrt \rho {\mathit{\boldsymbol{y}}_{\rm{R}}} $用于能量采集(EH, energy harvesting)接收端；$\sqrt {1 - \rho } {\mathit{\boldsymbol{y}}_{\rm{R}}} $用于信息接收端的信息解码(ID, information decode)，且能量切割因子0≤ρ≤1.采集到的能量信号表示为

$ \boldsymbol{y}_{\mathrm{R}-\mathrm{EH}}=\sqrt{\rho P_{\mathrm{s}}} \boldsymbol{H}_{\mathrm{SR}} \boldsymbol{S}+\boldsymbol{N}_{\mathrm{SR}} $

(1)

其中：P_s为信源传输功率, 信源产生比特信息，映射为多相移键控(MPSK, multiple phase shift keying)符号，MPSK调制符号为Q集合，即$Q = \left\{ {{a_i} = {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}i}}{M}}}|} \right.i \in \{ 0, 1, 2, \cdots , M - 1\} \} $，信源发送符号向量S=[s₁, s₂, …, s_NS]^T，H_SR为S-R的信道矩阵.这里讨论的是准静态独立瑞利衰落信道，此时H_SR~CN(0, 1), N_SR=[n₁, n₂, …, n_NR]^T为均值为0、方差为σ_SR²的加性高斯白噪声. (·)^T、(·)^H和Tr(·)分别表示矩阵的转置、共轭转置和矩阵的迹.

采集的能量为

$ E_{\mathrm{h}}=\xi \rho P_{\mathrm{s}}\left\|\boldsymbol{H}_{\mathrm{SR}}\right\|^{2} $

(2)

其中ξ表示能量转换效率.

信息接收端的信号表示为

$ \boldsymbol{y}_{\mathrm{R}-\mathrm{ID}}=\sqrt{(1-\boldsymbol{\rho}) P_{\mathrm{s}}} \boldsymbol{H}_{\mathrm{SR}} \boldsymbol{S}+\boldsymbol{N}_{\mathrm{SR}} $

(3)

中继信息接收端使用译码转发方式，采用最大似然算法，度量表达式为

$ \mathit{\boldsymbol{\hat S}} = \mathop {\arg \min }\limits_{\mathit{\boldsymbol{S}} \in Q} \parallel {\mathit{\boldsymbol{y}}_{{\rm{R}} - {\rm{ID}}}} - \sqrt {(1 - \rho ){P_{\rm{s}}}} {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}\mathit{\boldsymbol{S}}{\parallel ^2} $

(4)

第2阶段，中继到目的节点传输链路，即R-D链路.中继R对接收信号译码后转发，选择GSM-MBM方案.假设每根天线周围有m_rf个RF镜，有N_m=2^m_rf种镜像激活模式(MAP, mirror activation patterns).通过输入比特‘1’或‘0’分别控制RF镜的开或关. GSM-MBM系统包括N_T个基于媒介调制的发射单元(MBM-TU, media-based modulation-transmit unit)、N_a个RF射频链，N_a表示从N_T中激活发送的天线数. GSM-MBM信息比特通过MBM-TU索引、RF镜索引、相移键控调制符号3种方式传输.传输效率表示为

$ {\eta _{{\rm{GSM}} - {\rm{MBM}}}} = \left\lfloor {{\rm{lb}}\left( {\begin{array}{*{20}{c}} {{N_{\rm{T}}}}\\ {{N_{\rm{a}}}} \end{array}} \right)} \right\rfloor + {N_{\rm{a}}}{m_{{\rm{rf}}}} + {N_{\rm{a}}}{\rm{lb}}M $

(5)

其中$\left\lfloor \cdot \right\rfloor $表示向下取整.令S_m表示每个MBM-TU的N_m个MAP的集合. h_k^j=[h_{1, k}^j, h_{1, k}^j, …, h^j_{NR, k}]表示第j个MBM-TU的第k种MAP到接收天线的信道，h_{i, k}^j~CN(0, 1), 其中i∈[1:N_R], j∈[1:N_T]，k∈[1:N_m].则目的节点的接收信号表示为

$ {\mathit{\boldsymbol{y}}_{\rm{d}}} = \sqrt {{\mathit{\boldsymbol{P}}_{\rm{r}}}} \sum\limits_{j = 1}^{{N_{\rm{T}}}} {{{\hat s}_j}} \mathit{\boldsymbol{h}}_{{l_j}}^j + {\mathit{\boldsymbol{N}}_{{\rm{RD}}}} $

(6)

其中：P_r为中继传输功率，且P_r=E_h=ξρ×P_s‖H_SR‖²，$ {{\hat s}_j}$表示第j个MBM-TU的发送符号，l_j∈[1:N_m]表示当$ {{\hat s}_j}$ ≠0时第j个MBM-TU的MAP索引$\mathit{\boldsymbol{h}}_{{l_j}}^j \in {\mathit{\boldsymbol{H}}^j}, {\mathit{\boldsymbol{N}}_{{\rm{RD}}}} \sim {\rm{CN}}\left( {0, \sigma _{{\rm{RD}}}^2} \right), {\mathit{\boldsymbol{H}}^j} = \left\{ {\mathit{\boldsymbol{h}}_1^j, \mathit{\boldsymbol{h}}_2^j, \cdots } \right.\mathit{\boldsymbol{h}}_{{N_{\rm{m}}}}^i\} $，式(6)可以改写为

$ {\mathit{\boldsymbol{y}}_{\rm{d}}} = \sqrt {\xi \rho {P_{\rm{s}}}\parallel {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}{\parallel ^2}} \sum\limits_{j = 1}^{{N_{\rm{T}}}} {{{\hat s}_j}} {\mathit{\boldsymbol{H}}^j}{\mathit{\boldsymbol{e}}_{{l_j}}} + {\mathit{\boldsymbol{N}}_{{\rm{RD}}}} $

(7)

其中e_lj是N_m×1向量，其第l_j坐标为1，其他所有坐标为零.令H_RD=[H¹, H², …, H^N_T]为N_R×N_mN_T矩阵, 式(7)可以改写为

$ {\mathit{\boldsymbol{y}}_{\rm{d}}} = \sqrt {\xi \rho {P_{\rm{s}}}\parallel {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}{\parallel ^2}} {\mathit{\boldsymbol{H}}_{{\rm{RD}}}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{N}}_{{\rm{RD}}}} $

(8)

${{{\mathit{\boldsymbol{\hat S}}}_{{\rm{GSM}} - {\rm{MBM}}}} = \left\{ {\mathit{\boldsymbol{x}} = {{\left[ {\mathit{\boldsymbol{x}}_1^{\rm{T}}, \mathit{\boldsymbol{x}}_2^{\rm{T}}, \cdots , \mathit{\boldsymbol{x}}_{{N_{\rm{T}}}}^{\rm{T}}} \right]}^{\rm{T}}}:{\mathit{\boldsymbol{x}}_j} = {s_j}{\mathit{\boldsymbol{e}}_{{l_j}}}, {l_j} \in [1, {N_{\rm{m}}}];{s_j} \in {{\mathit{\boldsymbol{\hat S}}}_{{\rm{ GSM - MBM }}}}\} } \right.} $.

最后进行最大似然译码，判决度量可以表示为

$ \mathit{\boldsymbol{\hat x}} = \mathop {\arg \;\min }\limits_{\mathit{\boldsymbol{x}} \in {{\mathit{\boldsymbol{\tilde S}}}_{{\rm{GSM - MBM}}}}} \parallel {\mathit{\boldsymbol{y}}_{\rm{d}}} - \sqrt {\xi \rho {P_{\rm{s}}}\parallel {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}{\parallel ^2}} {\mathit{\boldsymbol{H}}_{{\rm{RD}}}}\mathit{\boldsymbol{x}}{\parallel ^2} $

(9)

2 性能分析

通过计算中继节点和目的节点处的平均成对错误概率(APEP, average pairwise error probability)来评估所考虑系统的整体性能.无线携能协作中继GSM-MBM方案的总误码率可以表示为

$ P_{\mathrm{b}} \leqslant P_{\mathrm{b}, 1}+P_{\mathrm{b}, 2}-2 P_{\mathrm{b}, 1} P_{\mathrm{b}, 2} $

(10)

P_{b, i}表示第i个链路的平均误码率；

$ {P_{{\rm{b}}, 1}} = \frac{1}{{{2^{{\eta _{{\rm{MIMO}}}}}}}}\sum\limits_\mathit{\boldsymbol{S}} {} \sum\limits_{\mathit{\boldsymbol{S}} \ne \mathit{\boldsymbol{\tilde S}}} {} P(\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}})\frac{{\delta (\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}})}}{{{\eta _{{\rm{ MIMO }}}}}} $

(11)

其中$ \delta (\mathit{\boldsymbol{S}}, {\rm{ }}\mathit{\boldsymbol{\tilde S}})$表示S与$ {\mathit{\boldsymbol{\tilde S}}}$不同的比特数，η_MIMO=N_TlbM表示MIMO的传输效率.

$ {P_{{\rm{b}}, 2}} = \frac{1}{{{2^{{\eta _{{\rm{GSM}} - {\rm{MBM}}}}}}}}\sum\limits_\mathit{\boldsymbol{x}} {} \sum\limits_{\mathit{\boldsymbol{x}} \ne \mathit{\boldsymbol{\tilde x}}} {} P(\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\tilde x}})\frac{{\delta (\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}})}}{{{\eta _{{\rm{GSM}} - {\rm{MBM}}}}}} $

(12)

其中$\delta (\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}}) $表示x与$ {\mathit{\boldsymbol{\tilde x}}}$不同的比特数, $P(\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}), P(\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\tilde x}}) $表示2个链路的APEP.

2.1 中继节点R的APEP

若源节点发送信号矩阵为S，给定信道矩阵H_SR已知，误判后码字矩阵为$ {\mathit{\boldsymbol{\tilde S}}}$，中继节点R的APEP表示为

$ P\left( {\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}|{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right) = Q\left( {\sqrt {\frac{{(1 - \rho ){P_{\rm{s}}}}}{{2\sigma _{{\rm{SR}}}^2}}\parallel {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}(\mathit{\boldsymbol{\tilde S}} - \mathit{\boldsymbol{S}}){\parallel ^2}} } \right) $

(13)

令信噪比$\gamma_{\mathrm{SR}}=\frac{(1-\rho) P_{\mathrm{s}}}{\sigma_{\mathrm{SR}}^{2}} $，式(13)表示为

$ P\left( {\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}|{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right) = Q\left( {\sqrt {\frac{\gamma }{2}\parallel {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}(\mathit{\boldsymbol{\tilde S}} - \mathit{\boldsymbol{S}}){\parallel ^2}} } \right) $

(14)

定义差错矩阵$ D(\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}}) = \mathit{\boldsymbol{\tilde S}} - \mathit{\boldsymbol{S}}$，令矩阵$ \mathit{\boldsymbol{A}}(\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}}) = D{(\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}})^{\rm{H}}} = \mathit{\boldsymbol{\tilde S}} - {\mathit{\boldsymbol{S}}^{\rm{H}}}\mathit{\boldsymbol{\tilde S}} - \mathit{\boldsymbol{S}}$，用λ_n，n=1, 2, …, N表示$ A(\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}})$的特征值，且λ_n≥0.对$ A(\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}})$奇异值分解，$ A(\mathit{\boldsymbol{S}}, \mathit{\boldsymbol{\tilde S}}) = V\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{V^{\rm{H}}}$，Λ表示特征值的对角矩阵，$ \parallel {\mathit{\boldsymbol{H}}_{{\rm{SR}}}}(\mathit{\boldsymbol{\tilde S}} - \mathit{\boldsymbol{S}}){\parallel ^2} = {\mathop{\rm Tr}\nolimits} \left[ {{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}V\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{V^{\rm{H}}}\mathit{\boldsymbol{H}}_{{\rm{SR}}}^{\rm{H}}} \right]$.用ζ_n表示H_SRV中的第n个元素，式(14)可以写为

$ P\left( {\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}|{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right) = Q\left( {\sqrt {\frac{\gamma }{2}\sum\limits_{n = 1}^N {{\lambda _n}} {{\left| {{\zeta _n}} \right|}^2}} } \right) $

(15)

利用Craig推导出Q函数，式(15)可以写为

$ \begin{array}{l} P\left( {\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}|{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right) = \\ \frac{1}{{\rm{ \mathit{ π} }}}\int_0^{\frac{{\rm{ \mathit{ π} }}}{{\rm{2}}}} {\exp } \left( {\frac{{ - \frac{\gamma }{2}\sum\limits_{n = 1}^N {{\lambda _n}} {{\left| {{\zeta _n}} \right|}^2}}}{{2{{\sin }^2}\theta }}} \right){\rm{d}}\theta = \\ \frac{1}{{\rm{ \mathit{ π} }}}\int_0^{\frac{{\rm{ \mathit{ π} }}}{{\rm{2}}}} {\prod\limits_{n = 1}^N {\exp } } \left( {\frac{{ - \gamma {\lambda _n}{{\left| {{\zeta _n}} \right|}^2}}}{{4{{\sin }^2}\theta }}} \right){\rm{d}}\theta \end{array} $

(16)

对于所有的n，|ζ_n|²服从具有2个自由度的χ分布, 有$f_{\chi}(x)=\exp (-x) $，且x>0.所以，对式(16)中的路径增益取平均，得

$ \begin{array}{l} P(\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}) = \mathit{\boldsymbol{E}}\left\{ {P\left( {\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}|{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right)} \right\} = \\ \frac{{\rm{1}}}{{\rm{ \mathit{ π} }}}\int_0^{\frac{{\rm{ \mathit{ π} }}}{{\rm{2}}}} {\left[ {\int_0^\infty {\prod\limits_{n = 1}^N {\exp } } \left( {\frac{{ - \gamma {\lambda _n}{{\left| {{\zeta _n}} \right|}^2}}}{{4{{\sin }^2}\theta }}} \right){f_\chi }(x){\rm{d}}x} \right]} {\rm{d}}\theta \end{array} $

(17)

利用矩生成函数，式(17)可以化为

$ P(\mathit{\boldsymbol{S}} \to \mathit{\boldsymbol{\tilde S}}) = \frac{{\rm{1}}}{{\rm{ \mathit{ π} }}}\prod\limits_{n = 1}^N {\int_0^{\frac{{\rm{ \mathit{ π} }}}{{\rm{2}}}} {\frac{{4{{\sin }^2}\theta }}{{4{{\sin }^2}\theta + \gamma {\lambda _n}}}} } {\rm{d}}\theta $

(18)

从式(18)可以看出，APEP取决于特征值λ_n和信噪比γ_SR.

2.2 目的节点D的PEP

GSM-MBM的最大似然规则由式(9)给出. x被解码为${\mathit{\boldsymbol{\tilde x}}} $的APEP可以写为

$ \begin{array}{l} P(\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\widetilde x}}) = \mathit{\boldsymbol{E}}\left\{ {P\left( {\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\widetilde x}}|{\mathit{\boldsymbol{H}}_{{\rm{RD}}}}} \right)} \right\} = \mathit{\boldsymbol{E}}[Q(\mathit{\boldsymbol{\sqrt {{ {\varPhi} }} }} )] = \\ \mathit{\boldsymbol{E}}\left[ {\frac{1}{2}{\mathop{\rm etfc}\nolimits} \left( {\frac{{\mathit{\boldsymbol{\sqrt {{ {\varPhi} }} }}}}{{\sqrt 2 }}} \right)} \right] \end{array} $

(19)

其中$ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \frac{{\xi \rho {P_{\rm{s}}}{{\left\| {{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right\|}^2}}}{{2\sigma _{{\rm{RD}}}^2}}{\left\| {{\mathit{\boldsymbol{H}}_{{\rm{RD}}}}(\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\widetilde x}})} \right\|^2}$，且Φ的概率密度函数根据文献[7]进行随机变量变换得到

$ {f_\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}(\varphi ) = \frac{1}{{\Gamma \left( {{N_{\rm{T}}}} \right){{\left( {{E_{\rm{h}}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right)}^{{N_{\rm{T}}}}}}}{\varphi ^{{N_{\rm{T}}} - 1}}\exp \left( { - \frac{\varphi }{{{E_{\rm{h}}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}}} \right) $

(20)

其中：$ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = D(x) = 1, {E_{\rm{h}}} = \xi \rho {P_{\rm{s}}}{\left\| {{\mathit{\boldsymbol{H}}_{{\rm{SR}}}}} \right\|^2}$.所以无条件的$ P\left( {\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\tilde x}}} \right)$表示为

$ P(\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\widetilde x}}) = \frac{1}{2}\int_{\varphi = 0}^\infty {{f_\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}} (\varphi ){\mathop{\rm etfc}\nolimits} \left( {\frac{{\mathit{\boldsymbol{\sqrt {{ {\varPhi} }} }}}}{{\sqrt 2 }}} \right){\rm{d}}\varphi $

(21)

在戈德史密斯^[7]的研究工作中，式(21)可以用封闭的形式计算:

$ P(\mathit{\boldsymbol{x}} \to \mathit{\boldsymbol{\widetilde x}}) = f{(\beta )^{{N_{\rm{T}}}}}\sum\limits_{k = 0}^{{N_{\rm{T}}} - 1} {\left( {\begin{array}{*{20}{c}} {{N_{\rm{T}}} - 1 + k}\\ k \end{array}} \right)} {(1 - f(\beta ))^k} $

(22)

其中：$ f(\beta ) = \frac{1}{2}\left( {1 - \sqrt {\frac{\beta }{{1 + \beta }}} } \right), \beta = \frac{{{E_{\rm{h}}}||\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\tilde x}}||{^2}}}{{4\sigma _{{\rm{RD}}}^2}}$.

由式(22)可知，R-D链路的误码率与第一链路S-R采集的能量有关，采集的能量越多，性能越好.

2.3 传输效率与复杂度分析

SM、SIMO-MBM、SM-MBM及GSM-MSM的传输效率与复杂度对比如表 1所示.可以看出，SIMO-MBM频谱效率比传统的单输入多输出系统有所提高，增加了m_rf比特，但是SIMO-MBM只有1根发射天线，可以使用的RF镜数量是有限的，而SM-MBM弥补了这一缺点，增加了天线数的选择，从而增加了传输效率.但是也可以看出，SM-MBM每次只激活单根天线，而GSM-MSM每次激活N_a根天线，所以GSM-MSM大大提高了传输效率.但是GSM-MSM检测复杂度与激活天线、镜像激活模式以及调制阶数呈指数级的增长，复杂度较高.

2.4 能耗增益

下面考虑所提方案在能耗方面的增益.系统消耗的总功率表示为

$ P=P_{\mathrm{s}}+P_{\mathrm{c}}-\xi \rho P_{\mathrm{s}}\left\|\boldsymbol{H}_{\mathrm{SR}}\right\|^{2} $

(23)

其中：P_s表示发射端的发射总功率，P_c表示收发机固定电路消耗(包括数模转换、频率合成等)的总功率.对于无线携能系统，能量采集补偿了一部分的系统消耗功率，ξρP_s‖H_SR‖².所以能耗增益表示为

$ | \text { Gain } |=10 \lg \left(\frac{P}{P_{\mathrm{s}}+P_{\mathrm{c}}}\right) $

(24)

当ξ=1, ρ=0.5时，可取P_s=1W，P_c=544MW^[8]，得出能耗增益为1.70dB.

3 仿真结果

通过计算机仿真了所提出的系统性能，为了更好地比较，对SM-MBM-SWIPT、SIMO-MBM-SWIPT和SM-SWIPT的系统性能也进行了仿真.在仿真中，假设发射机、接收机均确知信道状态信息.取P_s=1, N_S=4, N_T=4, N_R=4, N_a=2，能量转换效率ξ=1，能量切割因子ρ=0.5.

图 2所示为所提出的GSM-MBM-SWIPT的平均误码率性能与SM-MBM-SWIPT、SIMO-MBM-SWIPT和SM-SWIPT的比较结果，各方案的频谱效率统一为8bit·s^-1·Hz^-1. SIMO-MBM-SWIPT和SM-MBM-SWIPT采用的符号是(N_R, M, m_rf)和(N_T, N_R, M, m_rf), 用于SM和GSM-MBM的符号分别是(N_T, N_R, M)和(N_T, N_R，N_a, M, m_rf).由图 2可知，与需要16PSK的SIMO-MBM-SWIPT相比，在误码率为10^－4时，GSM-MBM-SWIPT的信噪比(SNR, signal-to-noise ratio)增益约为5dB，而且误码率为10^－4时，GSM-MBM-SWIPT与SM-MBM-SWIPT相比，SNR增益约为1dB.虽然SM比GSM-MBM-SWIPT提高了2dB增益，但SM-SWIPT需要的发射天线数却为64，大幅度提高了系统实现的复杂性，并增加了成本.

图 3所示为不同SNR下功率分配因子ρ对目的节点误码率性能的影响. ρ增加会增加收集的能量，从而提高R-D链路性能.然而，在S-R链路间中继节点处接收的SNR随着ρ值的增加而减小，S-R链路性能下降，所以ρ对整体性能具有2个相反的影响，这解释了图 3中曲线的凹形行为.然而，在不同的SNR下ρ存在不同的最佳值.

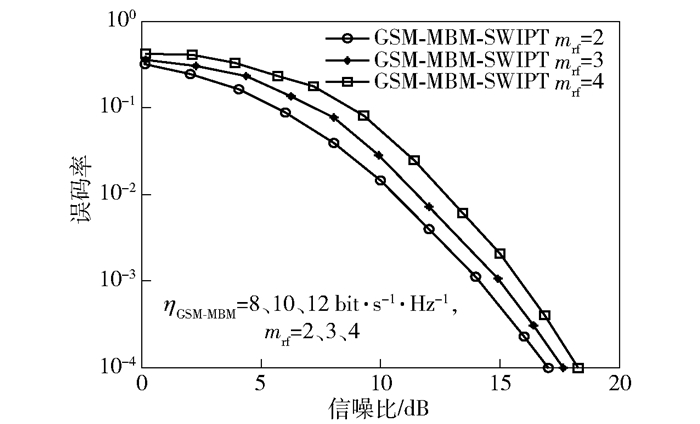
图 4示出了改变RF镜的个数对系统性能的影响. m_rf=2、3、4，系统的其他参数不变，相应的传输效率分别为8、10、12bit·s^-1·Hz^-1.由图 4可以看出，随着RF镜个数的增加，对应的误码率也依次增大.

4 结束语

为了提高SWIPT协作系统的传输效率，提出了GSM-MBM携能协作系统，并通过理论推导了传输效率、APEP和能耗增益，进行了蒙特卡罗仿真.仿真结果显示，与SIMO-MBM-SWIPT、SM-MBM-SWIPT相比，提出的方案不仅提高了传输效率，而且还降低了误码率、能耗；与SM-SWIPT系统相比较，在相同传输效率下误码率略高，但所需的发射天线数大幅度降低, 从而降低了系统实现的复杂性和成本.在不同的信噪比下，切割因子对误码率存在相反的影响，且存在不同最佳值. GSM-MSM-SWIPT无线携能协作系统提高了传输效率，但是其检测复杂度与激活天线、镜像激活模式以及调制阶数呈指数级的增长，所以后续需要研究GSM-MBM-SWIPT的低复杂度检测算法.