为实现网络开销与网络连通度的权衡设计,分别基于链路添加和链路删除提出2个启发式的拓扑构建算法.通过采用网络图的代数连通度,并定义无线链路的连通度开销比这一新的拓扑度量,计算每条链路在拓扑优化中的权值.所提的启发式算法可根据该链路权值进行无线链路的添加或删除.设计了若干网络开销函数,以满足不同的网络场景.仿真结果表明,所提的启发式算法能够生成低开销的网络拓扑,同时满足给定的连通度约束.
In order to achieve the tradeoff between network cost and network connectivity, two heuristic algorithms for topology control, which are based on link addition and link removal, respectively, are proposed. Each link's weight in the topology optimization is calculated by employing the theory of algebraic connectivity and introducing a new topology metric for each wireless link. The proposed algorithms add or delete a link according to its weight. We conceive some cost functions for different network scenarios. Simulations show that our proposed algorithms could generate the low-cost topologies under the network connectivity constraint.
无线网络(传感器网络、D2D网络等)被赋予了各种功能,能够支持越来越多的网络应用(环境监测、农业生产、军事应用等).然而,这些不同的应用对网络拓扑结构的要求也不尽相同.网络开销和网络连通度是2个重要的拓扑设计因素,通常它们是相互冲突的.如维持较多的无线链路,网络显然拥有较好的连通度.然而,网络连通度的提高却是以网络的能量消耗、干扰等开销的增加为代价的,故有必要在网络连通度的约束下,研究低开销的网络拓扑设计,即考查二者之间的权衡设计.
拓扑控制方面的研究多集中于网络的能量有效性上[1-3],忽视了网络连通度的重要性.采用传统的点/边连通度,Yan等[4]探讨了一维车联网能够保证k-点连通的充分必要条件;Ma等[5]通过构建路由树的方法提出了一种k-边连通的拓扑控制协议;Li等[6-8]在不同的网络环境中利用节点度探讨了可靠的拓扑构建方法.面向分层网络拓扑,Wang等[9]设计了负载均衡的成簇算法.基于网络的代数连通度,Cuomo等[10]和Gasparri等[11]分别研究了拓扑控制方法及连通维持准则.然则,这些工作均没有考虑网络开销这一因素.
笔者探讨网络开销和网络连通度权衡的网络拓扑设计.为无线链路定义一个新的拓扑度量,称为连通度开销比,即单位开销的网络连通度贡献量.由该定义出发,提出2个连通度约束下低开销的启发式拓扑控制算法.随后讨论若干常见的网络开销函数并进行算法仿真.
1 系统模型考虑无线网络G(V, E),其中节点集合表示为V={1, 2, …, n},链路集合为E={eij|i, j∈V}.链路的维持以及数据传输会消耗一定的网络资源,产生链路开销,如功率消耗、时延等.假设每条链路e的开销为c(e),并定义网络开销为网络拓扑中所有链路的开销之和,即
采用网络图的代数连通度,而非传统的点/边连通度,来刻画网络连通度.代数连通度不仅能够刻画网络的连通性好坏,还与一些实际应用有着紧密联系,如一致性估计[12].代数连通度a(G)定义为图拉普拉斯矩阵L的次小特征值.这里拉普拉斯矩阵L=D-A,其中D=diag({di})为图的节点度矩阵,di为节点i的邻节点个数(节点度),A为图的邻接矩阵.代数连通度a(G)有如下性质:① a(G)>0,当且仅当图G是连通图;②若G1由G2删除若干链路得到,则a(G1) < a(G2).于是,网络拓扑的连通性越好,其包含的链路就越多,相应地,网络图的代数连通度就越大.定义Θe=a(G)-a(G-e)为链路e在图G中的连通度贡献量,其中G-e表示从G中删除链路e得到的子图.另外,用记号G+e表示在G中添加链路e而得到的网络图.
需要研究的问题是,如何在代数连通度约束下,构建低开销的网络拓扑.给定一个初始网络拓扑G0(V, E0),目标是找寻一个子拓扑图Gobj(V, Eobj),使得Gobj具有最小的网络开销,即
一个基本的降低网络开销的方式是逐步删除具有最大开销的链路.然则,盲目地删除这些链路并不能实现研究目标.事实上,删除低连通度贡献的链路可以允许更多的链路删除,且不会过多地降低网络连通度.因此,如果一条链路具有较大的开销,但其连通度贡献量又较小,应当被首先移除.基于此,为每条链路定义一个新的拓扑度量,即
| $ \eta(e)=\frac{\mathit{\Theta}_{e}^{\alpha}}{c(e)} $ | (1) |
其中α为控制因子.该拓扑度量可以认为是链路e单位开销的连通度贡献量.
首先,计算初始拓扑G0中每条链路的η(e),根据该值将所有链路进行升序排列,并用Esort表示排序后的链路集合.随后,提出2个启发式拓扑控制算法.
基于链路添加的拓扑控制(TCLA, topology control with link addition)算法步骤如下:
1) 根据G0中每条链路负的η(e)值,计算G0的最小生成树.初始时,令G(V, E)为该最小生成树,Eres为剩余的可添加链路集合,即Eres=Esort-E,m=|Eres|.
2) 从Eres中选择第m条链路ewv∈E0,添加该链路到G中,即E=E+ewv,计算添加该链路后的代数连通度a(G+ewv).如果a(G+ewv)≥ath,则算法结束;否则,转至步骤3).
3) 令m=m-1,重复步骤2),直到遍历Eres中所有链路,即m=1.
基于链路删除的拓扑控制(TCLR, topology control with link removal)算法步骤如下:
1) 初始时,令G(V, E)=G0(V, E0),m=1.
2) 从Esort中选择第m条链路ewv∈E0,计算从G中删除该链路后的代数连通度a(G-ewv).如果a(G-ewv)≥ath,则从G中删除该链路,即E=E-ewv;否则,不删除该链路.
3) 令m=m+1,重复步骤2),直到遍历Esort中所有链路,即m=|Esort|.
TCLA算法步骤1)中的最小生成树保留了低开销、高连通度贡献的链路,并逐步进行链路添加.该算法在代数连通度高于ath时终止,见步骤2).而TCLR算法从初始拓扑开始,逐步删除高开销、低连通度贡献的链路.该算法在考查完所有链路后终止. 2个启发式算法每次迭代均将处理一条链路,网络的代数连通度将从a(G0)逐渐减少至ath或从0逐渐增加至ath.由于代数连通度的计算复杂度为O(n2),故2个启发式算法的计算复杂度均为O(|E0|n2).
3 链路开销函数启发式拓扑控制算法中采用的链路开销函数是任意的,可以根据实际应用进行定义.
功率消耗是一个常见的开销函数,在能量受限的无线网络(如传感器网络、物联网)中有着广泛的研究. 2个节点i和j能够相互通信,当且仅当它们的发射功率pi、pj均大于支持该链路的最小发射功率pijmin,即min {pi, pj}≥pijmin.在自由空间传播模型中,支持链路eij的最小发射功率pijmin可以表示为
| $ p_{i j}^{\min }=\frac{p_{\mathrm{th}}(4 \pi)^{2}}{H_{i} H_{j} \lambda^{2}} d_{i j}^{\tau} $ | (2) |
其中:pth为信号捕捉门限,Hi、Hj分别为节点i和j的天线增益,λ为波长,dij为节点i和j之间的距离,τ∈[2,4]为路径损耗因子.如果链路开销采用功率消耗函数,则算法生成的网络结构是连通度约束下功率有效的拓扑.
分组转发的不情愿性可以在资源(能量、带宽等)有限的无线网络中有效地分配网络资源.随着节点自身资源量的降低,节点会越来越不情愿地使用其珍贵资源.假设节点i当前可用资源为Ri.当节点i使用x单位的资源时,定义增函数gi(x)为资源定价函数.于是,设计节点i的一个不情愿性函数为
| $ U\left( {{R_i}, {r_i}} \right) = \int_{R_i^0 - {R_i}}^{R_i^0 - {R_i} + {r_i}} {{g_i}} (x){\text{d}}x $ | (3) |
其中:Ri0为节点i的初始资源量,ri(≤Ri)为分组转发时所需要的资源量.式(3)是可用资源Ri的减函数,所需资源量ri的增函数.定义链路开销c(eij)为该链路关联节点的不情愿性状态
| $ c\left(e_{i j}\right)=\ln \left(U_{i} U_{j}\right) $ | (4) |
如果链路开销采用不情愿性函数,则算法生成的拓扑结构能够根据节点当前的剩余资源动态调整,促使资源的均衡使用.
由于信道衰落及噪声的存在,在实际通信系统中也常采用分组错误率作为链路的开销函数.数据在高斯信道上传输的符号错误率ρs通常表示为
| $ Q=1-\left(1-\rho_{s}(\gamma)\right)^{M} $ | (5) |
采用Matlab对所提算法进行仿真实验.在仿真中,500m×500m的平面区域内随机均匀地分布60个网络节点.假设所有节点的覆盖范围是dmax=150m,用以生成初始拓扑.若2个节点在彼此的覆盖范围之内,二者可以直接通信,即链路存在.通常地,长距离链路意味着更高的功率消耗、严重的干扰以及分组错误率.因此,仿真中假设链路eij的开销cij正比于距离dij的二次方,即cij=Kdij2. K=10-5为常数,使得链路开销和连通度贡献量有相同的数量级.随机生成的初始网络拓扑可以由邻接矩阵以及对应的权值矩阵刻画.在这些包含拓扑信息的矩阵上执行提出的TCLA和TCLR算法,迭代地删除不必要链路,使之满足给定的连通度约束.
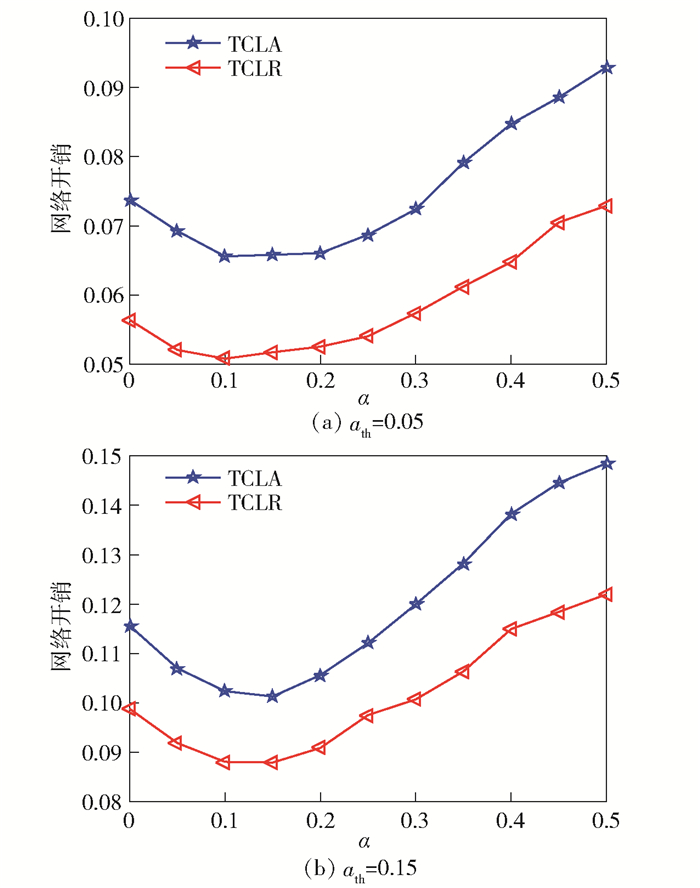
首先考查式(1)中的控制因子α对算法结果的影响,其中连通度约束分别取ath=0.05, 0.15.对于不同的α,图 1给出了算法所生成拓扑的网络开销.从图 1中可以看出,单一地考虑链路开销(即α=0)难以得到目标拓扑.这是由于拓扑中会保留大量的低开销链路,它们的和将会在整个网络开销中占有较大比例.因此,联合地考虑链路开销和连通度贡献量,才能使生成的拓扑结构具有尽可能低地网络开销.从图 1中可以看出,α取值为0.1附近时,所提出的算法具有最优的性能.此外,基于删除链路的TCLR算法优于基于添加链路的TCLA算法.这是由于TCLR算法能够考查网络中的所有无线链路,而TCLA算法在网络的代数连通度高于ath时终止.
|
图 1 控制因子对网络开销的影响 |
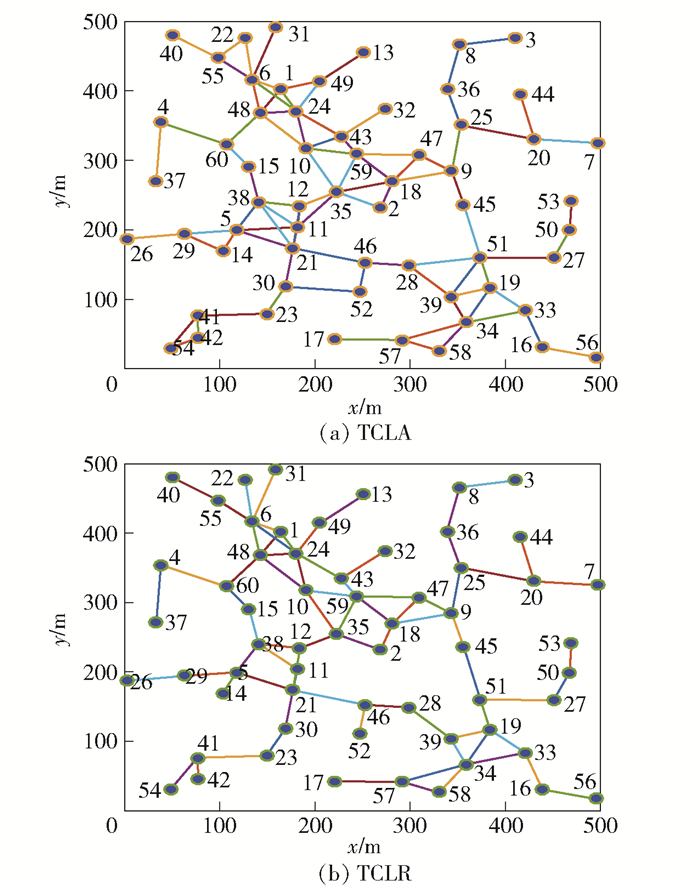
图 2、图 3给出了所提算法生成的网络拓扑图,其中连通度约束分别取ath=0.05, 0.15,控制因子α=0.1.随着连通度约束的增加,生成的拓扑图具有更多的链路和更高的网络开销.这一现象说明代数连通度可以很好地刻画拓扑的网络连通度.从图 2和图 3中可以看出,2个算法所得到的拓扑图仅有若干链路不同,即都尽可能地保留了低开销、高连通度贡献的链路.
|
图 2 连通约束ath=0.05时的拓扑 |

|
图 3 连通约束ath=0.15时的拓扑 |
最后考查连通度约束从0变化至0.5时,考查生成拓扑的网络开销. TCLA和TCLR算法分别取α=0.1可以获得较低的网络开销,取α=0(算法运行仅考虑链路开销)进行对比.同时,所提算法对比于基于代数连通度的能量节省(ESACON, energy saving based on algebraic connectivity)算法[10].图 4给出了网络开销随着网络连通度约束的变化曲线.从图 4中可以看出,网络开销随着连通度约束ath的增加而增加,意味着网络拓扑中包含了更多的链路.特别地,TCLR算法在α=0.1时生成的拓扑结构具有最小的网络开销.

|
图 4 网络开销与连通度约束 |
网络开销与网络连通度是无线网络拓扑设计的2个重要指标.为此,基于网络拓扑控制研究如何权衡网络开销与网络连通度.首先根据每条链路的开销和连通度贡献量定义一个新的拓扑度量,即单位开销的连通度贡献.随后提出2个拓扑控制算法,尽可能地降低网络拓扑开销,同时满足给定的连通度约束.最后仿真结果说明了所提算法的有效性.
| [1] |
Zhao X, Zhang Y, Jiang C, et al. Mobile-aware topology control potential game:equilibrium and connectivity[J]. IEEE Internet of Things Journal, 2016, 3(6): 1267-1273. DOI:10.1109/JIOT.2016.2587102 |
| [2] |
Xu M, Yang Q, Kwak K. Algebraic connectivity aided energy-efficient topology control in selfish ad hoc networks[J]. Wireless Networks, 2017, 23(5): 1331-1341. DOI:10.1007/s11276-016-1217-z |
| [3] |
Waqas A, Mahmood H. A game theoretical approach for topology control in wireless ad hoc networks with selfish nodes[J]. Wireless Personal Communications, 2017, 96(1): 249-263. DOI:10.1007/s11277-017-4165-8 |
| [4] |
Yan Z, Jiang H, Shen Z, et al. -connectivity analysis of one-dimensional linear VANETs[J]. IEEE Transactions on Vehicular Technology, 2012, 61(1): 426-433. DOI:10.1109/TVT.2011.2176969 |
| [5] |
Ma G, Yang Y, Qiu X, et al. Fault-tolerant topology control for heterogeneous wireless sensor networks using multi-routing tree[C]//2017 IFIP/IEEE Symposium on Integrated Network and Service Management. Lisbon: IEEE Press, 2017: 620-623.
|
| [6] |
Li X, Cai J. Topology control for guaranteed connectivity provisioning in heterogeneous sensor networks[J]. IEEE Sensors Journal, 2016, 16(12): 5060-5071. DOI:10.1109/JSEN.2016.2549543 |
| [7] |
Shi Y, Sun H, Sheng M, et al. Constructing a robust topology control for reliable communications in multi-channel cognitive radio ad hoc networks[J]. IEEE Communications Magazine, 2018, 56(4): 172-179. DOI:10.1109/MCOM.2018.1700730 |
| [8] |
刘洲洲, 彭寒. 基于节点可靠度的无线传感器网络拓扑控制算法[J]. 吉林大学学报(工学版), 2018, 48(2): 571-577. Liu Z Z, Peng H. Topology control algorithm based on node reliability in WSN[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(2): 571-577. |
| [9] |
王恒, 夏枢洋, 王平. 适用于工业无线WIA-PA网络的负载均衡成簇方法[J]. 北京邮电大学学报, 2017, 40(2): 29-35, 42. Wang H, Xia S Y, Wang P. Load-balanced clustering scheme for WIA-PA industrial wireless networks[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(2): 29-35, 42. |
| [10] |
Cuomo F, Abbangnale A, Cianfrani A, et al. Keeping the connectivity and saving the energy in the internet[C]//INFOCOM. Shanghai: IEEE Press, 2011: 319-324.
|
| [11] |
Gasparri A, Sabattini L, Ulivi G. Bounded control law for global connectivity maintenance in cooperative multirobot systems[J]. IEEE Transactions on Robotics, 2017, 33(3): 700-717. DOI:10.1109/TRO.2017.2664883 |
| [12] |
Lorenzo P, Barbarossa S. Distributed estimation and control of algebraic connectivity over random graphs[J]. IEEE Transactions on Signal Processing, 2014, 62(1): 5615-5628. |


