2. 北京邮电大学 信息与通信工程学院, 北京 100876;
3. 北京市网络与体系架构重点实验室, 北京 100876
针对多用户多中继非正交多址(NOMA)接入系统,提出了基于全双工解码转发的多用户最佳中继NOMA系统.基于最大最小准则,提出了可使目的用户获得信息速率最大化的最佳中继选择方案;分析了目的用户中断概率,推导了其闭合表达式.仿真结果表明,若不考虑优化的用户排序,所提最佳中继选择方案的优势与用户个数和中继转发功率有关;若考虑优化的用户排序,采用所提最佳中继选择方案始终可以实现最佳的目的用户性能.
2. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. Beijing Key Laboratory of Network System Architecture and Convergence, Beijing 100876, China
Considering the multi-user and non-orthogonal multiple access (NOMA) system, a multi-user and best relay NOMA system with full-duplex decode-and-forward was proposed. A best relay selection scheme was further proposed to maximize the achievable target user's information rate via max-min criterion. Then, the target user's outage probability was analyzed, and the closed-form expression was also given. The simulation results showed that, the advantage of the proposed best relay selection scheme was related with the number of users and the transmit power of the relay without regard to the optimal users' order. However, if the optimal users' order was taken into account, the best performance can be always be achieved by the proposed best relay selection scheme.
非正交多址接入(NOMA,non-orthogonal multiple access)技术是第5代移动通信系统(5G)中一种可有效提高频谱效率的关键技术[1].研究表明, NOMA相比传统正交多址方案可有效提高频谱利用率[2].
NOMA技术最重要的优势是信道条件好的用户可以为信道条件差的用户提供服务.关于协作中继NOMA系统的研究正在如火如荼的进行. Men等[3]基于NOMA系统,考虑一个基站通过单个放大转发(AF,amplify-forward)中继与多个移动端同时通信,对系统中断概率性能进行了分析. Liu等[4]则考虑基于NOMA的蜂窝网络中,利用距离基站较近的用户作为中继为远端用户提供中继协作. Men等[5]考虑基于NOMA的单源单中继多天线网络,分析了当中继采用半双工(DF,decode-and-forward)方式时的系统中断性能. Zhong等[6]进一步考虑NOMA系统存在2个用户和一个中继的场景,并分析了全双工中继模式下用户的中断性能. Ding等[7]考虑具有一个基站多个中继的NOMA系统,对中继的选择策略进行了研究,但是仅考虑了利用一个中继协助目的用户传输数据.
关于多用户中继协作传输在传统正交多址系统中已经得到了大量研究[2, 8],但在NOMA系统中多中继的协作传输还尚未有深入研究.基于此,笔者首次考虑蜂窝网络中存在多个中继同时为多个用户提供服务的场景,考虑中继采用DF协议,提出了一种可使目的用户获得信息速率最大化的最佳中继选择方案,分析了目的用户中断概率闭合表达式.最后,通过仿真验证了所提方案的优势.
1 系统模型考虑典型的下行链路环境,提出了系统包多用户最佳中继NOMA系统,包括一个基站(S,station)和N+1个用户,如图 1所示.每个节点配置单天线,S和N+1个用户之间的链路服从独立同分布的瑞利衰落,用hS-n表示S到第n (n=0, 2, …, N)个用户的信道条件,据此建立了NOMA系统模型,N+1个用户根据其信道质量进行排序[2],|hS-0|2 < |hS-1|2 < … < |hS-N|2.为了表示方便,省去时间量值.考虑第0个用户(目的节点0)的信道条件太差无法接收到来自S的信息,其它N个用户均可作为中继节点Ri(i=1, 2, …, N)为其转发数据.虽然从S到中继链路(S→Ri)的信道质量是最好的,但是Ri→D的信道条件却不一定最优.而S→Ri链路和Ri→D链路对于目的节点性能的影响情况尚未有明确结论.因此,需要分析哪一条链路对目的用户的性能影响更大,还需要综合考虑两条链路给出优化的中继选择方案.下面先给出系统信号模型和每个节点可实现的信息速率.

|
图 1 多用户最佳中继NOMA系统模型 |
S发送包括N+1个用户消息的下行复合NOMA信号
| $ {y_i} = {h_{S - i}}\sum\limits_{n = 0}^N {{{\sqrt {{P_n}x} }_n}} + {n_i} $ | (1) |
其中:hS-i为S→Ri链路上的信道衰落系数;ni~CN(0, σ2)为S→Ri链路上的加性高斯白噪声.
所有中继接收到复合NOMA信号后,利用SIC技术将目的信号x0进行解码,然后,根据最佳中继(BR,best relay)选择准则,选出一个最佳的中继将其解码估计的信号
| $ y_{D}=h_{\mathrm{BR}-D} \sqrt{P_{\mathrm{R}}} x_{\mathrm{BR}}+n_{D} $ | (2) |
其中:hBR-D为BR→D链路上的信道衰落系数;nD~CΝ(0, σD2)为BR→D链路上的加性高斯白噪声.
2 性能分析 2.1 最佳中继选择方案根据NOMA技术原理,所有的中继都将利用串行干扰删除技术先对x0进行解码,则在第一个阶段,Ri对x0进行解码时,将把第j(j>i)个用户信号视为干扰信号,此时可获得的信号干扰噪声比为
| $ {R_{{R_i}}} = \frac{{{P_0}{{\left| {{h_{S - i}}} \right|}^2}}}{{\sum\limits_{j = i + 1}^N {{P_j}} {{\left| {{h_{S - i}}} \right|}^2} + {\sigma ^2}}} $ | (3) |
在第2个阶段,D将接收到来自BR转发的信号,假设选择第i个中继作为最佳中继BR,则hBR-D链路上可获得的信号干扰噪声比为
| $ R_{R_{i} D}=\frac{P_{i}\left|h_{R_{i}-D}\right|^{2}}{\sigma^{2}} $ | (4) |
根据全双工中继解码转发原理,考虑带宽归一化,结合式(3)和式(4),当选择Ri作为最佳中继时,从S到目的端D可获得的总的信息速率可表示为
| $ C_{D}^{R_{i}}=\operatorname{lb}\left(1+\min \left(R_{R_{i}}, R_{R_{i} D}\right)\right) $ | (5) |
目标是使得目的端可获得的信息速率最大,故所提最佳中继选择准则为
| $ \begin{array}{*{20}{c}} {{\text{BR}} = \mathop {\arg \max }\limits_i \left( {\min \left( {{R_{{R_i}}}, {R_{{R_i}D}}} \right)} \right), } \\ {i \in \{ 1, 2, \cdots , N - 1\} } \end{array} $ | (6) |
对于本文考虑的如图 1所示系统模型而言,当目的端可获得的信息速率小于目标传输速率
| $ C_{\mathrm{opt}}=\operatorname{lb}\left(1+\mathop {\max }\limits_i \left(\min \left(R_{R_{i}}, R_{R_{i} D}\right)\right)\right) $ | (7) |
将式(3)和式(4)代入式(7)可得
| $ \begin{gathered} {C_{{\text{opt}}}} = \operatorname{lb} \left( {1 + \mathop {\max }\limits_i \left( {\min \left( {\frac{{{P_0}{{\left| {{h_{S - i}}} \right|}^2}}}{{\sum\limits_{j = i + 1}^N {{P_j}} {{\left| {{h_{S - i}}} \right|}^2} + {\sigma ^2}}}} \right.} \right.} \right., \hfill \\ \left. {\frac{{{P_i}{{\left| {{h_{{R_i} - D}}} \right|}^2}}}{{{\sigma ^2}}}))} \right) \hfill \\ \end{gathered} $ | (8) |
当用户获得的信息速率小于目标传输速率时,将发生中断现象.因此,当目标传输速率为
| $ P_{\mathrm{out}}=\operatorname{Pr}\left\{C_{\mathrm{opt}} <\widetilde{R}\right\} $ | (9) |
为了求解式(9),令
| $ \begin{array}{*{20}{l}} {{P_{{\text{ out }}}} = \Pr \left\{ {\mathop {\max }\limits_i (\min (X, Y)) < {2^{\tilde R}} - 1} \right\} = } \\ {\prod\limits_{i = 1}^{N - 1} {\left( {1 - \Pr \left\{ {X > {2^{\tilde R}} - 1} \right\}\Pr \left\{ {Y > {2^{\tilde R}} - 1} \right\}} \right)} } \end{array} $ | (10) |
其中
| $ \begin{gathered} \Pr \left\{ {X > {2^{\tilde R}} - 1} \right\} = \hfill \\ \left\{ {{P_0} > \left( {{2^{\tilde R}} - 1} \right)\sum\limits_{j = i + 1}^N {{P_j}} , {{\left| {{h_{S - i}}} \right|}^2} > \frac{{\left( {{2^{\tilde R}} - 1} \right){\sigma ^2}}}{{{P_0} - \left( {{2^{\tilde R}} - 1} \right)\sum\limits_{j = i + 1}^N {{P_j}} }}} \right\} \hfill \\ \end{gathered} $ | (11) |
考虑|hS-n|2, n=0, 1, …, N和|hRi-D|2服从瑞利衰落.如果不考虑用户按信道条件排序[9],则任意两个节点a和b之间的信道条件|ha-b|2的概率密度函数可表示为
| $ f_{\left|h_{a-b}\right|^{2}}(y)=\frac{1}{\lambda_{a b}} \mathrm{e}^{-\frac{\gamma}{\lambda_{a b}}} $ | (12) |
其中λab为瑞利衰落系数.将式(12)代入式(11),可得
| $ {\exp \left( { - \frac{{\left( {{2^{\tilde R}} - 1} \right){\sigma ^2}}}{{\left[ {{P_0} - \left( {{2^{\tilde R}} - 1} \right)\sum\limits_{j = i + 1}^N {{P_j}} } \right]{\lambda _{S - i}}}}} \right)} $ | (13) |
如果考虑用户按信道条件排序,则根据文献[2],排序的|hS-n|2的概率密度函数PDF可表示为
| $ \begin{gathered} {f_{{{\left| {{h_{S - n}}} \right|}^2}}}(x) = \hfill \\ {Q_n}\sum\limits_{j = 0}^{N - n} {{{( - 1)}^j}} \left( {\begin{array}{*{20}{c}} {N - n} \\ j \end{array}} \right)\frac{1}{{{\lambda _{S - n}}}}{{\text{e}}^{ - \frac{x}{{\lambda _{S - n}}}}}{\left( {1 - {{\text{e}}^{ - \frac{x}{{{\lambda _{S - n}}}}}}} \right)^{n + j - 1}} \hfill \\ \end{gathered} $ | (14) |
其中
| $ \begin{array}{*{20}{c}} {\Pr \left\{ {X > {2^{\tilde R}} - 1} \right\} = } \\ {{Q_i}\sum\limits_{j = 0}^{N - i} {{{( - 1)}^j}} \left( {\begin{array}{*{20}{c}} {N - i} \\ j \end{array}} \right)\frac{1}{{{\lambda _{S - i}}}}\int_A^\infty {{{\text{e}}^{ - \frac{x}{{{\lambda _{S - i}}}}}}} {{\left( {1 - {{\text{e}}^{ - \frac{x}{{{\lambda _{S - i}}}}}}} \right)}^{i + j - 1}}{\text{d}}x} \end{array} $ | (15) |
利用指数扩展形式,式(15)可进一步写为式(16).同理,结合式(10)和式(13),可以得到
| $ \operatorname{Pr}\left\{Y>2^{\tilde{R}}-1\right\}=\exp \left(-\frac{\left(2^{\tilde{R}}-1\right) \sigma^{2}}{P_{i} \lambda_{R_{i}-D}}\right) $ | (16) |
综合式(10)~式(14),可以得到,当不考虑用户按信道条件排序时,系统中断概率可计算如式(17)所示。当考虑用户按信道条件排序时,系统中断概率可计算如式(18)所示
| $ \begin{gathered} {P_{{\text{ out }}}} = \hfill \\ \prod\limits_{i = 1}^{N - 1} {\left( {1 - \exp \left( { - \left( {\frac{{\left( {{2^{\bar R}} - 1} \right){\sigma ^2}}}{{\left[ {{P_0} - \left( {{2^{\tilde R}} - 1} \right)\sum\limits_{j = i + 1}^N {{P_j}} } \right]{\lambda _{S - i}}}} + } \right.} \right.} \right.} \hfill \\ \frac{{\left( {{2^{\tilde R}} - 1} \right){\sigma ^2}}}{{{P_i}{\lambda _{{R_i} - D}}}}))) \hfill \\ \end{gathered} $ | (17) |
由于对于任意一个中继而言,从基站到中继的信道条件和从中继到目的端的信道条件是不同的,
| $ \begin{gathered} {P_{{\text{out}}}} = \prod\limits_{i = 1}^{N - 1} {\left( {1 - {{\text{e}}^{ - \frac{{(2\tilde R - 1){\sigma ^2}}}{{{P_i}{\lambda _{{R_i}}} - D}}}}{Q_i}\sum\limits_{j = 0}^{N - i} {{{( - 1)}^j}} \left( {\begin{array}{*{20}{c}} {N - i} \\ j \end{array}} \right) \times } \right.} \hfill \\ \left( {\sum\limits_{l = 0}^{i + j - 1} {\frac{{{{( - 1)}^l}}}{{l + 1}}} \left( {\begin{array}{*{20}{c}} {i + j - 1} \\ l \end{array}} \right){{\text{e}}^{ - \frac{{\left( {l + 1} \right)\frac{{(2\tilde R - 1){\sigma ^2}}}{{{P_0} - (2\tilde R - 1)\sum\limits_{j = i + 1}^N {{P_j}} }}}}{{{\lambda _{S - i}}}}}}} \right)) \hfill \\ \end{gathered} $ | (18) |
为了直观地比较哪一条链路对目的用户的性能影响更大,仿真中对比了四种中继选择方案:选择任意中继、选择使基站到中继链路最大化(Max-SR)的中继、选择使中继到目的节点链路最大化(Max-RD)的中继以及本文最大最小中继方案(Max-Min).
图 2所示为当不考虑用户根据其信道条件排序时目的用户可获得的信道容量C.其中,图 2(a)为N=2, 中继转发功率PR=10dB时,在不同的中继选择方案下,目的用户可获得的信道容量随发射信噪比SNR的变化情况.可以看出,当发射信噪比SNR大于11dB时,最大最小最佳中继选择方案优于其他方案.而当SNR小于11dB时,Max-SR方案可以使得目的用户获得更高的信道容量,也就是说,此时,基站到中继节点链路的信道条件对目的用户的性能影响更大.由图 2(b)可以看出,当N=2且中继转发功率PR=20dB时,Max-SR方案始终是最优的,当发射信噪比SNR大于17dB时,Max-SR方案和Max-Min方案可以使得目的用户获得相同的性能.由图 2(c)和(d)可以看出,当N=4时,Max-Min方案始终可以使目的用户获得最佳的信道容量.

|
图 2 目的用户信道容量随发射信噪比的变化 |
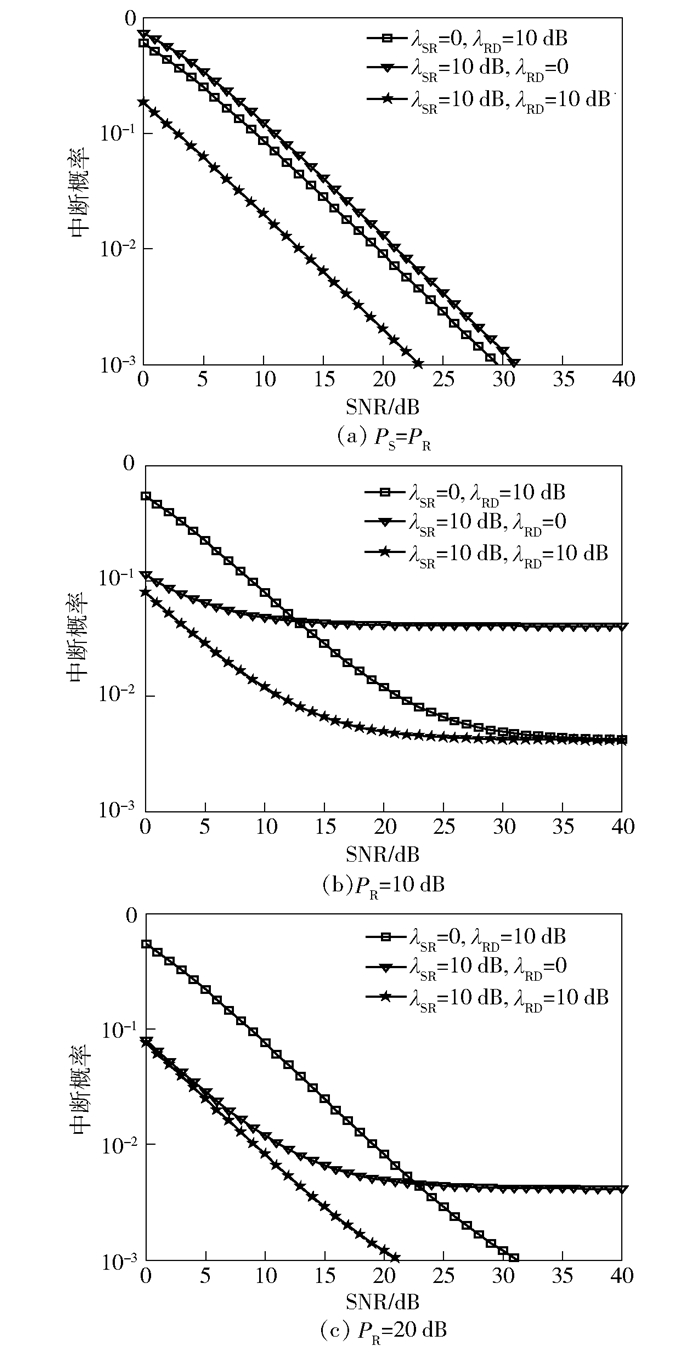
图 3所示为采用Max-Min方案时,目的用户中断概率在不同中继链路条件下随发射信噪比的变化情况.其中,λSR表示基站到中继链路的信道平均衰落系数,λRD表示中继到目的端链路的信道平均衰落系数.图 3(a)为中继转发功率与基站发射功率相同的情况,可以看出,当λSR=0dB且λRD=10dB时的目的用户中断概率小于λSR=10dB且λRD=0时的目的用户中断概率,说明,通过改善中继到目的端链路的信道条件可以更好地提高目的用户中断性能.图 3(b)为PR=10dB时的情况,可以看出,如果中继转发功率一定而与基站发射功率无关时,当基站发射信噪比SNR大于12dB时,λSR=0且λRD=10dB时的目的用户中断概率小于λSR=10dB且λRD=0时的目的用户中断概率,而当基站发射信噪比SNR小于12dB时,λSR=0且λRD=10dB时的目的用户中断概率大于λSR=10dB且λRD=0时的目的用户中断概率.而由图 3(c)可以看出,当PR=20dB时,该分界点将会增大变为22dB.
|
图 3 目的用户中断概率随发射信噪比的变化 |
因此可以得出,基站到中继链路信道条件和中继到目的端链路信道条件对于目的用户性能的影响程度与中继转发功率有关.
图 4所示为不同用户数下目的用户中断概率随目标传输速率的变化情况.仿真中,PS=PR=10dB.可以看出,随着目标传输速率的增加,目的用户中断概率会增大,但是会趋于平稳趋势.随着用户数的增加,趋于平稳的渐近值会降低,这是因为随着用户数的增加,分配给目的用户的功率会降低,因此会导致用户很难实现目标传输速率要求;而当目标传输速率较低时,随着用户数的增加,目的用户中断概率会降低,这是因为中继的选择范围增大.

|
图 4 目的用户中断概率随目标传输速率的变化 |
图 5所示为考虑用户根据其信道条件进行排序时不同中继选择方案下目的用户可获得的信道容量.其中,N=2,中继转发功率PR=20dB.可以看出,基本上在整个SNR范围内,Max-Min方案均优于其他方案. Max-SR方案次之,而任意中继方案性能最差.

|
图 5 信道排序条件下目的用户信道容量随发射信噪比的变化 |
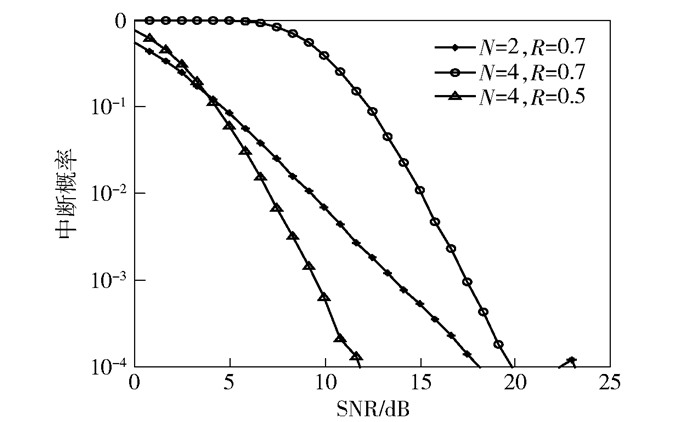
图 6所示为采用Max-Min方案时,目的用户中断概率在不同用户数及目标传输速率条件下随发射信噪比的变化情况.可以看出,当N=4且R=0.7时目的用户的中断概率大于N=2且R=0.7时目的用户的中断概率,这是因为当N=4时,目的用户作为最差链路用户分配到的功率变小,故中断概率增大.而当N=4且R=0.5时,目的用户的中断概率降低,甚至低于N=2且R=0.7时目的用户的中断概率,也就是说,作为服务质量要求不高的最差信道用户而言,其中断概率可以低于服务质量要求高的信道质量比较好的用户,满足NOMA同时为多用户提供服务的设计初衷.
|
图 6 目的用户中断概率随发射信噪比的变化 |
对全双工中继转发模式下的多用户最佳中继NOMA系统性能进行了分析,并给出了不同中继选择方案下性能的对比情况.需要说明的是,笔者仅从最佳中继协作传输的角度分析了最差用户的性能改善情况,后续将考虑全网用户的工作情况,对多中继NOMA协作传输进行深入研究.
| [1] |
Ding Zhiguo, Liu Yuanwei, Choi J, et al. Application of non-orthogonal multiple access in LTE and 5G networks[J]. IEEE Communications Magazine, 2017, 55(2): 185-191. DOI:10.1109/MCOM.2017.1500657CM |
| [2] |
李美玲. 基于中继的协作频谱感知性能分析及优化[J]. 通信学报, 2013, 34(9): 33-40. Li Meiling. Performance analysis and optimization of cooperative spectrum sensing with relay[J]. Journal on Communications, 2013, 34(9): 33-40. |
| [3] |
Men Jinjin, Ge Jianhua, Zhang Chensi. Performance analysis of non-orthogonal multiple access for relaying networks over Nakagami-m fading channels[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 1200-1208. DOI:10.1109/TVT.2016.2555399 |
| [4] |
Liu Yuanwei, Ding Zhiguo, Elkashlan M, et al. Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 938-953. DOI:10.1109/JSAC.2016.2549378 |
| [5] |
Men Jinjin, Ge Jianhua. Non-orthogonal multiple access for multiple-antenna relaying networks[J]. IEEE Communications Letters, 2015, 19(10): 1686-1689. DOI:10.1109/LCOMM.2015.2472006 |
| [6] |
Zhong Caijun, Zhang Zhaoyang. Non-orthogonal multiple access with cooperative full-duplex relaying[J]. IEEE Communications Letters, 2016, 20(12): 2478-2481. DOI:10.1109/LCOMM.2016.2611500 |
| [7] |
Ding Zhiguo, Dai Huaiyu, Poor H V. Relay selection for cooperative NOMA[J]. IEEE Wireless Communications Letters, 2016, 5(4): 416-419. DOI:10.1109/LWC.2016.2574709 |
| [8] |
Zou Yulong, Yao Yudong, Zheng Baoyu. Cognitive transmissions with multiple relays in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(2): 648-659. DOI:10.1109/TWC.2010.120610.100830 |
| [9] |
Lei Hongjiang, Zhang Jianming, Park K H, et al. On secure NOMA systems with transmit antenna selection schemes[J]. IEEE Access, 2017, 5: 17450-17464. DOI:10.1109/ACCESS.2017.2737330 |


