基于软定义无线电(SDR)和虚拟机(VM)迁移技术的云无线接入网(C-RAN)是第5代移动通信系统(5G)系统中的一种灵活架构,基于该架构提出了一种优化算法,可以根据系统状态动态计算基带处理单元(BBU)的最佳负载范围,并考虑用切换效率来控制额外的资源消耗.仿真结果表明,该算法能够自动选取合适的BBU工作负载范围,并在较低的切换损耗下维持BBU在该范围内工作.
Cloud radio access network (C-RAN) based on software defined radio (SDR) and virtual machine (VM) migration is a flexible architecture in the fifth generation of mobile communications system (5G). Based on the system model, we propose an optimization algorithm to choose the best base band unit (BBU) working load instead of configuring it as a constant value according to experience. The switching quality is also introduced to control the extra resource cost caused by the switching process. Simulation results show that the proposed algorithm can calculate the optimized working range for each BBU and keep the BBUs working in optimized range with low switching costs.
第5代移动通信系统(5G)中云无线接入网(C-RAN, cloud radio access network)作为一种可以大大提高资源利用效率的灵活型架构方案,引起了越来越多研究者的关注. C-RAN通过集中式的基带处理单元(BBU, base band unit)和分布式的射频拉远单元(RRH, remote radio head)来集中管理运算处理资源,通过灵活调整BBU-RRH的配对关系来实现资源复用,提高资源利用效率.
C-RAN在引入基于软定义无线电(SDR, software defined radio)和虚拟机(VM, virtual machine)迁移的网络功能虚拟化技术后,带来了资源灵活编排的优势[1],如何开发高效的分配算法也成为了研究的热点之一.
基于Wang等[2]提出的系统模型和系统性能评估方法,对快速切换场景下的C-RAN系统进行了研究,提出了一种最优化算法.该算法可以根据系统工作状态对BBU的工作负载进行均衡,以较低的切换损耗,动态维持BBU在性能最好的负载范围内进行工作,最后给出仿真结果和分析.
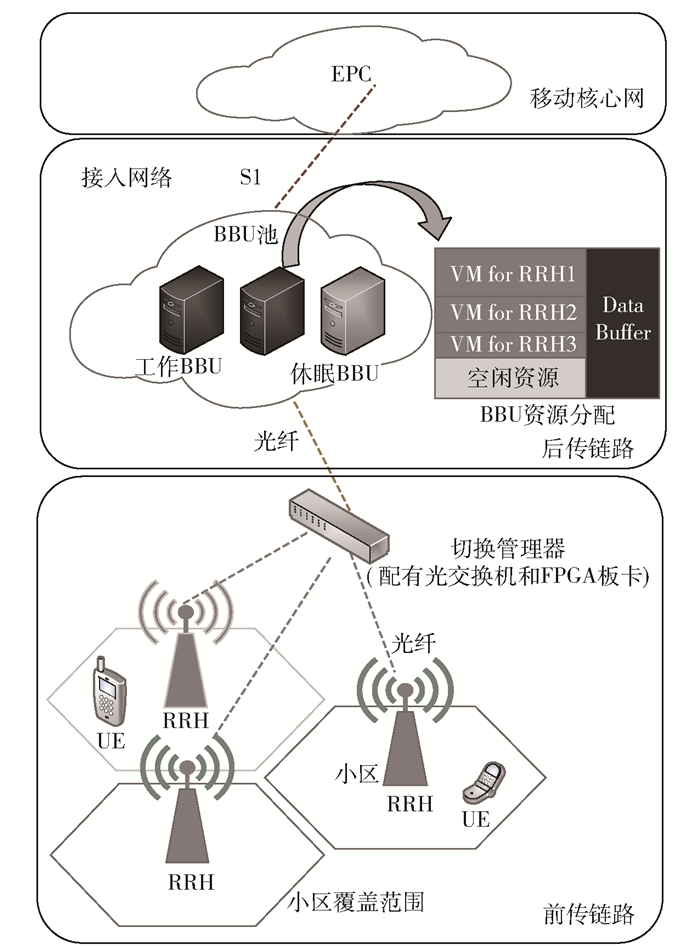
1 C-RAN系统及BBU-RRH切换原理 1.1 C-RAN系统架构基于SDR和VM迁移的C-RAN系统架构如图 1所示.
|
图 1 C-RAN系统架构 |
多个BBU组成一个云化的BBU池,每个BBU中可以运行多个VM,每个VM上运行一套SDR系统,用于实现对应的RRH的基带处理功能.每个RRH与其对应的VM之间通过光纤经由配有光交换机和对应FPGA板卡的切换控制器连接,采用通用无线接口(CPRI, common public radio interface)进行通信.每个VM可以根据资源调度方案在不同的BBU中进行迁移来平衡BBU池中每个BBU的处理负载. VM迁移后,切换管理器通过调整相应的BBU-RRH光交换接口,保证VM与对应RRH间的配对关系不被改变,从而达到BBU池中处理资源集中调度、负载均衡、提高资源利用率的效果.
1.2 BBU-RRH切换流程C-RAN系统会设定一个固定的切换间隔,每次到达切换间隔会根据该段时间内不同VM的处理负载和每个BBU的负载状况制定切换方案,然后通过虚拟机热迁移的方式实现资源的重分配.
系统通过一个切换间隔时间的观测并根据预先设定的工作范围,将BBU根据工作负载分为高负载(超出工作范围)、中负载(位于工作范围中)、低负载(低于工作范围)、休眠(没有VM在其中运行,BBU处于休眠状态,基本不消耗电量)4类.文献[2-3]中的算法均为预先设置固定的BBU工作负载上下界,所提算法则是根据观测情况动态调整BBU工作范围.
切换方案的制定主要是将高负载的BBU中部分VM迁移出去来降低负载使其处于中负载状态;向低负载BBU中迁入VM来使其达到中负载状态;或者将其中的VM全部迁出,并切换为休眠状态来降低系统损耗.切换完成时,应保证大部分BBU都处于中负载状态,即位于设定的工作范围.
在制定好切换方案之后,切换方案的执行主要由虚拟机热迁移实现.虚拟机热迁移流程主要包含准备过程、数据传输过程和结束过程三步.分别实现的是在迁入BBU中预启动迁入VM、进行迁移数据传输、关闭迁出BBU中的迁出VM并改变BBU-RRH连接等功能.
热迁移整个流程所需时间根据平台不同需要数秒至数十秒,服务中断时间为毫秒级,当以秒为单位设置迁移间隔时,停机时间对SDR系统的实时性影响很小[4].
2 系统性能评估方法通过采用文献[2]中的评估方法,主要对阻滞资源,空闲资源和切换损耗进行计算,并通过设置相应的权值计算整体系统性能.
2.1 无线资源和计算处理资源匹配C-RAN系统资源可分为无线资源和计算处理资源.无线资源主要是指整个系统拥有的无线传输资源,由RRH与UE之间的信道容量决定.计算处理资源主要是指BBU的计算资源,用于处理每个RRH的上下行数据.
C-RAN系统通过将多个BBU整合在一起形成资源池,集中分配计算处理资源,可以保证较高的计算资源利用效率.由于无线信道的实时变化特性,所需求的计算资源会实时波动.如果分配的计算资源不足,会导致部分数据处理不完,造成部分无线资源浪费[5].同时,当BBU-RRH切换频率提高到数秒量级时,由于虚拟机迁移带来的迁移损耗,即额外的计算处理资源浪费和停机带来的损耗,也要进行考虑和计算.
2.2 评估公式对于C-RAN系统性能的评估主要包括无线资源浪费、计算处理资源浪费和额外切换损耗.其中无线资源浪费和计算处理资源浪费主要是由两者的不匹配所造成的.如果定义第i个BBU用于处理数据传输的资源为
| $ A_{i}=C-N_{i} V $ | (1) |
其中:C为该BBU的总处理资源,Ni为其中运行的VM数量,V为维持每个VM运行的最低处理资源.这里所有资源的计算单位均为bit/s, 即以所能服务的上下行数据传输速率为计算单位[2].定义该BBU在t时刻处理无线业务所需的处理资源为
| $ D_{i}(t)=\sum\limits_{j=1}^{N_{i}} R_{i, j}(t), R_{i, j}(t) \in R_{i} $ | (2) |
其中Ri为与该BBU连接的所有RRH集合,Ri, j(t)为该时刻处理第j个RRH所有数据业务所需的计算处理资源.
那么在时间(0, τ)内,该BBU因为不能提供足够的计算处理资源而浪费的无线资源,即阻滞资源可表示为
| $ B_{i}\left(0, \tau, A_{i}, R_{i}\right)=\frac{1}{\tau} \sum\limits_{i=0}^{\tau} \max \left(D_{i}(t)-A_{i}, 0\right) $ | (3) |
同理,该BBU的空闲资源可表示为
| $ I_{i}\left(0, \tau, A_{i}, R_{i}\right)=\frac{1}{\tau} \sum\limits_{i=0}^{\tau} \max \left(A_{i}-D_{i}(t), 0\right) $ | (4) |
切换损耗可表示为
| $ {S_i}(t) = \sum\limits_{k = 1}^{{{\hat N}_i}} {{{\hat R}_{i, k}}} (t) + {\hat N_i}V $ | (5) |
其中:
假设虚拟机迁移过程消耗的总时间为t0,那么在一个切换间隔时间内,整个系统的性能评估为
| $ \begin{array}{*{20}{c}} {E(0, \tau ) = \frac{1}{\tau }\sum\limits_{i = 1}^M \alpha {B_i}\left( {0, {t_0}, {{\hat A}_i}, {{\hat R}_i}} \right) + }\\ {\beta {I_i}\left( {0, {t_0}, {{\hat A}_i}, {{\hat R}_i}} \right) + \chi \sum\limits_{i = 0}^{{t_0}} {{S_i}} (t) + }\\ {\frac{1}{\tau }\sum\limits_{i = 1}^M \alpha {B_i}\left( {{t_0}, \tau , {A_i}, {R_i}} \right) + \beta {I_i}\left( {{t_0}, \tau , {A_i}, {R_i}} \right)} \end{array} $ | (6) |
其中:
根据所述评估方法,当第i个BBU的运算处理资源为Ai时,该BBU的评估函数为
| $ \begin{array}{*{20}{c}} {{G_i}\left( {0, \tau , {A_i}, {R_i}} \right) = \frac{1}{\tau }\sum\limits_{t = 0}^\tau {\left[ {\alpha \max \left( {{D_i}(t) - {A_i}, 0} \right) + } \right.} }\\ {\left. {\beta \max \left( {{A_i} - {D_i}(t), 0} \right)} \right]} \end{array} $ | (7) |
可整理为
| $ {G_i}\left( {0, \tau , {A_i}, {R_i}} \right) = \frac{1}{\tau }\left( {{m_i}\beta - {n_i}\alpha } \right){A_i} + \frac{1}{\tau }\sum\limits_{t = 0}^\tau {D_i^*} (t) $ | (8) |
其中
| $ D_{i}^{*}(t)=\left\{\begin{array}{ll}{D_{i}(t), } & {D_{i}(t) \geqslant A_{i}} \\ {-D_{i}(t), } & {D_{i}(t)<A_{i}}\end{array}\right. $ | (9) |
因为Di(t)为离散时间序列,则应当存在k1和k2满足:
| $ \left. {\begin{array}{*{20}{l}} {{m_i}\beta - {n_i}\alpha > 0, }&{{A_i} > {D_i}\left( {{k_1}} \right)}\\ {{m_i}\beta - {n_i}\alpha = 0, }&{{D_i}\left( {{k_1}} \right) \le {A_i} \le {D_i}\left( {{k_2}} \right)}\\ {{m_i}\beta - {n_i}\alpha < 0, }&{{A_i} < {D_i}\left( {{k_2}} \right)} \end{array}} \right\} $ | (10) |
那么分段函数Gi(0, τ, Ai, Ri)在Ai>Di(k1)时单调递增,在Ai < Di(k2)时单调递减,Di(k1)≤Ai≤Di(k2)时取得最小值.记该最小值为min (Gi),因为需要取最优工作范围,而且该最小值只有在完美预测情况下才可取到,所以通过因子γ来扩充最优工作范围.
假设
| $ \left. {\begin{array}{*{20}{l}} {{\mu _i} < {{\tilde A}_{i, 1}} < {D_i}\left( {{k_1}} \right) < {D_i}\left( {{k_2}} \right) < {{\tilde A}_{i, 2}}}\\ {{G_i}\left( {0, \tau , {\rm{ }}{{\tilde A}_{i, 1}}, {R_i}} \right) = {G_i}\left( {0, \tau , {\rm{ }}{{\tilde A}_{i, 2}}, {R_i}} \right) = \gamma \min \left( {{G_i}} \right)} \end{array}} \right\} $ | (11) |
那么当BBU资源总量为Pi且满足
| $ \left. {\begin{array}{*{20}{l}} {\inf \left( {{P_i}} \right) > C, }&高负载\\ {\inf \left( {{P_i}} \right) \le C \le \sup \left( {{P_i}} \right), }&中负载\\ {\sup \left( {{P_i}} \right) < C, }&低负载\\ {{P_i} = 0, }&休眠 \end{array}} \right\} $ | (12) |
在制定切换方案时可先根据评估公式计算其切换效率,来决定是否进行该迁移操作,切换效率为
| $ \begin{array}{*{20}{c}} {{Q_{{i_1}, {i_2}}}\left( {0, \tau , {{\hat R}_{{i_1}, {i_2}}}} \right) = {G_{{i_1}}}\left( {0, \tau , C - {N_{{i_1}}}V, {R_{{i_1}}}} \right) + }\\ {{G_{{i_2}}}\left( {0, \tau , C - {N_{{i_2}}}V, {R_{{i_2}}}} \right) - {E_{{i_1}, {i_2}}}\left( {0, \tau , {{\hat R}_{{i_1}, {i_2}}}} \right)} \end{array} $ | (13) |
其中
| $ \begin{array}{*{20}{c}} {{E_{{i_1}, {i_2}}}\left( {0, \tau , {{\hat R}_{{i_1}, {i_2}}}} \right) = }\\ {{G_{{i_1}}}\left( {0, {t_0}, C - {N_{{i_1}}}V - {{\hat N}_{{i_1}}}V, {R_{{i_1}}} \cup {{\hat R}_{{i_1}, {i_2}}}} \right) + }\\ {{G_{{i_2}}}\left( {0, {t_0}, C - {N_{{i_2}}}V, {R_{{i_2}}}} \right) + \chi \sum\limits_{t = 0}^{{t_0}} {{S_{{i_1}}}} (t) + }\\ {{G_{{i_1}}}\left( {{t_0}, \tau , C - {N_{{i_1}}}V - {{\hat N}_{{i_1}}}V, {R_{{i_1}}} \cup {{\hat R}_{{i_1}, {i_2}}}} \right) + }\\ {\quad {G_{{i_2}}}\left( {{t_0}, \tau , C - {N_{{i_2}}}V + {{\hat N}_{{i_1}}}V, {R_{{i_1}}}\backslash {{\hat R}_{{i_1}, {i_2}}}} \right)} \end{array} $ | (14) |
当切换效率为正时执行该切换操作,否则重新计算切换计划.
4 仿真结果在仿真中,对照2种已有切换方案[2],在固定的场景下选取不同的工作范围测试其系统性能,并与优化算法进行比较.
仿真参数设置为20个BBU和400个RRH,每个BBU总容量C为1 Gbit/s,V为15 Mbit/s,迁移时间为3 s,切换间隔为8 s,最小单位时间为1 ms,权值为α=49, β=1, χ=10,扩充因子取值为γ=1.1.每个RRH的业务设定为每秒包到达率λ为100的泊松分布,每个数据包大小服从σ为1.37,μ0为8.37的对数正态分布[6].
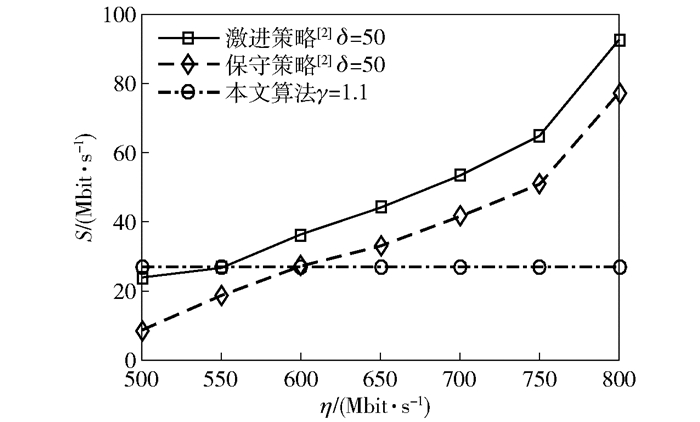
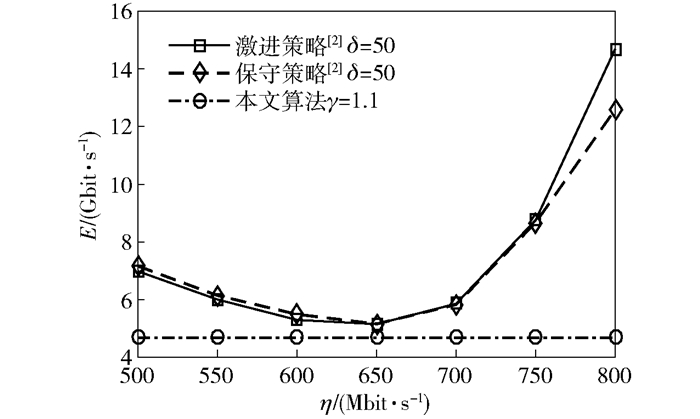
图 2~图 4所示分别为阻滞资源、空闲资源和切换损耗随工作范围变化的曲线. η为每个BBU的工作范围中心点,δ=50 Mbit/s为工作范围距离中心点的浮动.由图 2~图 4可以看到,文献[2]介绍的切换方案在工作范围取值增加时,阻滞资源随之增加,空闲资源减小,切换损耗由于更加频繁的切换也随之增加.而所提出的优化算法通过权值的调整保证了阻滞资源和空闲资源的相对平衡,同时由于考虑了切换效率,切换损耗一直保持在一个较低的值上. 图 5所示为系统综合性能,可以看出,所提出优化算法的整体性能比该场景下文献[2]中算法枚举出的最优解还要好.

|
图 2 阻滞资源 |

|
图 3 空闲资源 |
|
图 4 切换损耗 |
|
图 5 系统总体性能 |
在5G网络中,架构的灵活调整会导致资源分配问题复杂化,如何有效地评估资源分配方案,并制定合理的优化算法是一个关键研究点.基于资源利用效率提出了一种根据C-RAN系统负载情况动态调整BBU负载的优化算法,下一步可根据该算法对C-RAN系统进行性能分析和优化,并利用机器学习相关算法进行研究.
| [1] |
Checko A, Christiansen H, Yan Y, et al. Cloud RAN for mobile networks-a technology overview[J]. IEEE Communications Surveys & Tutorials, 2017, 17(1): 405-426. |
| [2] |
Wang Y, Zhang X, Yang D. Evaluation methodology for fast switching cloud ran systems[J]. IEEE Communications Letters, 2017, 21(11): 2404-2407. DOI:10.1109/LCOMM.2017.2733526 |
| [3] |
Sigwele T, Pillai P, Hu Y F. iTREE: intelligent traffic and resource elastic energy scheme for cloud-ran[C]//FiCloud 2015. Rome: IEEE Press, 2015: 282-288.
|
| [4] |
Akoush S, Sohan R, Rice A. Predicting the performance of virtual machine migration[C]//IEEE MASCOTS 2010. Miami: IEEE Press, 2010: 37-46. https://www.researchgate.net/publication/224176254_Predicting_the_Performance_of_Virtual_Machine_Migration
|
| [5] |
Liao Y, Song L, Li Y, et al. How much computing capability is enough to run a cloud radio access network?[J]. IEEE Communications Letters, 2017, 21(1): 104-107. DOI:10.1109/LCOMM.2016.2615612 |
| [6] |
Chen Y, Wang W, Fu L, et al. Traffic model for http video page[C]//International Conference on Communications and Networking in China (CHINACOM). Hangzhou: IEEE Press, 2008: 432-436.
|


