针对物联网系统复杂应用环境中由关键节点失效导致的系统拓扑结构的脆弱性问题,提出了一种抗毁性k-连通拓扑结构的构建方法.首先把系统分成若干个互不交叠的簇,然后对网络中存在的关键节点进行检测,并利用簇头节点的移动性构建以关键节点为中心的局部k-连通拓扑结构,达到去除关键节点和提高网络抗毁性的目的.构建了簇间的k-连通拓扑结构,给出了物联网智能安防系统应用仿真实验,并通过节点的介数中心性、网络的平均连通度和网络的鲁棒性验证了所提抗毁性方案的可行性和有效性.
To enhance the system topology vulnerability caused by the failure of critical nodes in the Internet of Things (IoT) system based complex application environments, a construction method of the survivable k-connected topology is proposed. Firstly, all nodes of network system are classified into non-overlapping clusters. Then, the cut points existed in the network are detected, and the cut point centered a local k-connected topology is constructed by use of the motion of the cluster head nodes, so that the critical nodes can be effectively removed to improve the network survivability. Finally, all the cluster head nodes are selected to form the backbone network which also acts as the global inter-cluster k-connected topology. The proposed method is evaluated by the simulation in an IoT-based intelligent monitoring system. The results proves the feasibility and validity of the proposed method in terms of the betweeness centrality of nodes, the network average connectivity and the network robustness.
物联网作为第四次工业革命核心技术之一,通过人与人、人与物以及物与物之间的互联,实现环境与状态信息实时共享以及智能化采集、传输、处理、执行[1-2].物联网系统终端局部信息交互,进而实现物联网系统整体规划和人类社会与物理系统的融合.通过可靠感知物理世界人、机、物、环境异构全要素信息,将动态网络环境下的海量感知数据实时传输至信息层,集成规约多源多模态异构数据,并精准控制混杂动态环境下异构执行器资源协同工作[3-4].
在复杂和恶劣的应用环境中,由于能量的有限性、任务的对抗性与节点感知的局限性等因素容易导致系统节点失效进而引发系统拓扑结构的断裂,从而影响系统的功能和任务的完成.网络拓扑结构的抗毁性和健壮性是物联网系统协同完成任务的关键. Fan等[5]提出了无线传感器网络的概率覆盖算法来增强网络拓扑的覆盖面积. Dai等[6]构建了一个k-连通的k-支配集作为骨干网络来平衡效率和网络的容错性. Basu等[7]通过移动网络中的某些节点到新的位置,使网络构建成双连通的,以提高网络的抗毁性. Rosset等[8]提出分布式k-连通算法,对每个sink节点的邻居节点进行k-值检测. Varadarajan等[9]针对移动机器人网络,提出了一种新颖的基于节点移动的拓扑控制方案,将静态节点和移动节点放在一个不规则的六边形中,结合动态拓扑管理,提高网络的可靠性和连通性.基于分簇的层次型拓扑结构可有效对节点进行管理,节点能耗得以减少并具有较好的网络可扩展性[10-11].笔者着眼于关键节点导致的物联网系统拓扑结构的脆弱性问题,提出一种抗毁性能较强的层次型物联网系统拓扑构建方法,并以物联网智能安防应用系统进行了仿真验证.
1 系统模型与相关定义系统模型:将n个移动节点随机放置在二维方形监控区域中.用无向图G=(V, E)表示节点拓扑结构.如果两个节点i和j之间可以进行正常的信息交互,则ρij=1,否则ρij=0.系统中,若任意节点对之间的欧式距离小于等于节点的通信半径R,即dis(vi, vj)≤R,并且ρij=1,则说明节点i和j能够进行信息交互.其中λn={1, 2…n},V(G)={vi, i∈λn}为系统节点集合,E(G)=(vi, vj)|vi, vj∈V & dis(vi, vj) < R & ρij=1表示系统边集,即系统中节点之间存在的通信链路集合.
笔者引入以下相关定义与假设:
定义1 在图G中,如果顶点对vi与vj间存在两条路径,并且除了顶点vi与vj之外这两条路径中不存在相同顶点,那么这两条路径就被称作顶点不相交路径.
定义2 如果无向图G任意两个节点之间至少存在一条路径,那么这个图是单连通图.
定义3 若无向图G至少含有3个顶点,当且仅当任意两个顶点i, j∈V之间存在两条顶点不相交的路径(i, j),则图G是双连通的.
定义4 在图G(t)=(V(t), E(t))中的t时刻,如果去除其中任意k-1个节点,不会使图的连通分量增加,也就是说,如果任意两个节点之间至少存在k-条顶点不相交的路径,那么图G是k-连通的.
定义5 对于无向图G=(V, E)中的任意一个节点vi,若存在另外一个节点vj,使得这两个节点之间的欧式距离dis(vi, vj)小于等于通信半径R,即dis(vi, vj)≤R,并且满足ρvivj=1,则将节点vj称作节点vi的1-跳邻居节点(1-跳邻居),记作vj∈N1(vi).
定义6 节点vi的1-跳邻居图由vi、vi的1-跳邻居节点N1(vi)和这些节点间构成的边集组成,即Gvi1=(vi∪N1(vi), Evi1)⊂G,其中Evi1={(vi, vj)|dis(vi, vj)≤R&ρvivj=1},vj∈N1(vi).
假设1 系统初始化阶段,节点之间拓扑结构是一个连通的网络.每个节点具有唯一ID,能够获取自身位置信息,通信半径R可调整,平时处在静止状态,能按需移动.
2 系统模型与相关定义k-连通拓扑结构基于层次型分簇拓扑构建.分簇是将整个网络划分为若干个单元簇,每个簇由1个簇头节点和若干个簇内成员节点组成.簇头构成高一级的骨干网络,进而使网络形成层次型的拓扑结构.簇头负责簇内节点数据采集和簇间数据转发.分簇有利于节点的层次化管理与系统的扩展. k-means算法可使样本聚类成k个簇.
笔者提出的k-连通拓扑控制方法由3阶段组成:第1个阶段是节点分簇;第2个阶段是簇内局部k-连通拓扑控制;第3个阶段是簇间k-连通拓扑控制.
1) 采用k-means算法把系统节点分成若干个互不相交叠的簇.首先随机选取k个聚类质心,计算样本距离k个聚类质心的距离,将样本归类为距离最小时的质心对应的类,然后重新计算该类的质心,直至所有k个质心向量都不再发生变化.
2) 当簇内节点拓扑好之后,在每个簇中检测关键节点,采用Harary图的思想,通过给关键节点的1-跳邻居节点逆时针排序,使关键节点的1-跳邻居节点构建成连通的拓扑结构,从而使得关键节点与其1-跳邻居节点共同构建成局部的2连通或者局部3连通拓扑结构来达到去关键节点的目的,消除关键节点对网络的影响.
3) 在去除关键节点的每个簇中选举簇头,簇头之间同样采用Harary图来构建k-连通的拓扑结构.
2.1 簇内局部k-连通拓扑结构的构建分簇后,给定每个节点相同的通信半径.节点的接收信号强度的计算公式为
| $ R=P_{t}-L\left(d_{0}\right)-10 \eta \lg \left(\frac{d}{d_{0}}\right) $ | (1) |
其中:Pt是节点发射功率,d0是参考距离,L(d0)是参考距离为d0时的传输损耗,η是路径损耗指数. d是发送方与接收方的距离.当d为节点的通信半径时,此时R为接收信号强度的阈值(R_threshold).当节点vi发送信号时,节点vj的接收信号强度R大于接收信号强度阈值时,则节点vi和节点vj存在信息交互边(vi, vj).
每个簇中关键节点的判定是构建簇中局部k-连通拓扑结构的基础.本文使用基于深度优先搜索(DFS)的方法来判断关键节点.
深度优先搜索的过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问1次.无向图用DFS遍历时,能获得1棵DFS搜索树. 图 1(a)是无向图,图 1(b)是DFS搜索树.遍历开始的起始顶点称为根节点.在DFS过程中访问未访问过的顶点时所经过的边,称为树边(父子边),如图 1(b)中的实线所示.在DFS过程中碰到已经访问的顶点时所经过的边,称为回边(返祖边、后向边).在DFS搜索树,存在两类节点可能是关键节点:

|
图 1 无向图的深度优先搜索 |
1) 根节点u至少有两棵子树,则u为关键节点;
2) 对于非叶子节点u的子树中的节点,若其不存在指向u的祖先节点的回边,则去除u之后,搜索树中的其他部分与u的子树的节点不再连通,则u为关键节点.
在深度优先搜索过程中,节点u被遍历到的顺序号用num(u)表示,节点u或u的子树用非父子边能达到的深度最小的祖先节点用low(u)表示,那么low(u)的计算公式为
| $ \operatorname{low}(u)=\left\{\begin{array}{ll}{\min \{\operatorname{low}(u), \operatorname{low}(v)\}, } & {(u, v)}为树边 \\ {\min \{\operatorname{low}(u), \operatorname{num}(v)\}, } & {(u, v)}为树边\end{array}\right. $ | (2) |
其中:(u, v)为回边,并且v不为u的父节点.
对于第1类关键节点,若只存在一颗子树,即整个图是强连通,则删掉根节点,必然不会变为多个子图,所以也不是关键节点.只有至少存在两颗子树,删除根节节点,才能变成多于一个的子图,此时根节点才是关键节点.
对于第2类关键节点,当(u, v)为树边且满足low(v)>num(u)时,节点u才能成为关键节点,也即是u的子孙唯有经过u才能访问u的祖先.若删除u,则至少分成两个子图.
识别出每个簇中的关键节点之后,采用Harary图的思想来构造簇中局部k连通的拓扑结构H(k, n).其中k-表示网络的连通度,n表示节点的个数.将n个节点逆时针标记为1~n,按照下面的规则构造k-连通的Harary图.
1) 如果所需构建的连通性k是偶数,令k=2m,然后将每个节点与每个方向上与该点相邻的m个节点相连,即可以得到所需构建的拓扑图.
2) 如果所需构建的连通性k是奇数,节点的个数n是偶数,则令k=2m+1,首先构造出H(2m, n),然后当
3) 如果所需构建的连通性k是奇数,节点的个数n是奇数,则令k=2m+1,首先构造出H(2m, n),当
当关键节点的1-跳邻居集(1-跳邻居节点)个数n为2时,则可以移动关键节点的邻居节点,使得关键节点的1-跳邻居节点进入彼此的信息交互范围内.则关键节点和其1-跳邻居节点3个节点就构成了局部2连通网络(局部双连通图),删除任意一个节点,剩余两个节点依然可以进行通信,相比于之前的局部单连通网络,双连通图网络的连通度得到增强,进而提升了系统的抗毁性.
当关键节点的1-跳邻居节点数n大于等于3时,可以将这n个节点构建一个H(k, n)图,则H(k, n)图与关键节点一起构成了一个局部k+1连通的拓扑结构,从而达到去除关键节点的目的.当关键节点的邻居节点数比较多时,可以仅构建H(2, n)图,最终构建成以关键节点为中心的局部3连通图.
当检测到系统存在关键节点时,关键节点的1-跳邻居节点根据相对关键节点的极角的大小进行逆时针排序后,再根据构建Harary图的规则,关键节点可以计算出所需添加的信息交互边,当关键节点发现某些节点的发射功率不能达到所需的发射功率时,关键节点就发送相应的位置调整信息来调节此节点的位置,使其进入其他节点的信息交互范围内,成为彼此的邻居节点.如果节点移动后产生新的关键节点则继续对新的关键节点根据构建Harary图的规则去关键节点.
图 2和图 3给出了局部k连通(局部2-连通或者局部3-连通)构建算法的实例. 图 2(a)中1号节点是关键节点,2、3号节点是它的1-跳邻居节点,从图 2(a)中可以看出2号节点和3号节点需要添加新的信息交互边来构建以关键节点为中心的局部2连通图.关键节点根据Harary图首先计算出两邻居节点通信所需的发射功率,如果两节点的传输功率小于所需的发射功率,那么关键节点告知节点2向节点3的位置移动,直到进入节点3的信息交互范围内.从而得到期望的如图 2(b)所示的局部2-连通图. 图 3(a)中1号节点是关键节点,2~5节点是关键节点的1-跳邻居节点,从图 3(a)中可以看出5号和2号节点,3号和4号节点需要添加新的信息交互边来构建以关键节点为中心的局部3连通图.关键节点根据Harary图,首先计算出各个节点通信所需的发射功率,如图 3(a)中5号和2号节点的发射功率小于5号和2号节点通讯所需的功率,那么关键节点告知节点5向节点2的位置移动,直到进入节点2的信息交互范围内.同理,如果3号节点和4号节点的发射功率小于3号节点和4号节点通信所需的功率,那么关键节点告知节点3向节点4的位置移动,直到进入节点4的信息交互范围内.从而得到期望的如图 3(b)所示的局部3-连通图.

|
图 2 局部2-连通拓扑结构构建实例 |

|
图 3 局部3-连通拓扑构建实例 |
簇内局部k-连通拓扑结构构建好之后,选出每个簇的簇头来构建簇间k-连通拓扑结构.簇头的选举依据簇内节点的权值W的大小来确定.因为用k-means聚类算法进行分簇时会有k个聚类质心,距离聚类质心越近的节点其与簇内其他节点进行通信所需的总通信代价越小,无线网络中节点可达邻居节点数通常为6~8,此时网络的性能较好[12].权值公式为
| $ W=w_{1} \frac{1}{D_{1}}+w_{2} \frac{D_{2}}{7} $ | (3) |
其中:w1和w2为权重因子,D1为节点到聚类质心的距离,D2为节点的度.在每个簇中选择权值最大的节点为簇头,如果两节点权值大小相同则选择节点编号较小的一个为簇头.
簇头节点之间的k-连通拓扑结构的构建同样也采用Harary图的思想.构建簇间k-连通拓扑结构以及簇头节点将收集到的簇内信息进行数据传输时,簇内成员节点可以进入休眠阶段以节省能量.
簇间拓扑控制阶段,簇头的通信半径可变.每个簇头节点根据Harary图的规则计算出构建k-连通拓扑结构所需的最大通信半径即最大发射功率,作为其通信半径.构建k-连通拓扑结构至少有k+1个节点.如图 4所示,用4个簇头节点构建3连通拓扑结构为例来阐述簇头节点最大通信半径的确定. 图 4中首先选取位置最低的一个节点作为1号节点,然后其他簇头节点按照与1号节点的极角的大小逆时针排序的编号为2、3和4.按照Harary图的规则,需要将1号与2号节点、2号与3号节点、3号与4号节点、1号与3号节点、2号与4号节点进行通信来构建3连通的拓扑结构图. 1号节点与2、3、4号节点进行通信所需的半径分别为R1、R2、R3.因为图中R1和R3都小于R2,所以1号与2、3、4号节点进行通信所需的半径至少为R2.同理,2号节点所需的通信半径至少为R4,3号节点所需的通信半径至少为R2,4号节点所需的通信半径至少为R4.

|
图 4 3-连通图构建实例 |
如果系统中簇头受到恶意攻击或者由于其他原因失效,可以依据簇头选取的原则,再次从簇内选取节点以代替失效的簇头节点.
基于第2节所述拓扑构建思路,算法策略伪代码如算法1所示.
算法1 抗毁性k-连通拓扑构建算法
输入:网络中的参数;
do k-means;
while(t=nUCT)
do DFS检测每个簇中的关键节点;
if存在关键节点
then识别出存在的关键节点;
构建以关键节点为中心的局部k-连通拓扑结构;
if网络中不存在簇头或者簇头失效
then选举出簇头;
构建簇间k-连通拓扑结构;
系统进行信息的收集和传递;
end
该算法对网络中关键节点进行实时检测,以避免关键节点失效导致网络分割及网络协同任务的失败.
3 仿真实验与评价分析采用Matlab仿真平台,对本文抗毁性拓扑构建方法模拟并分析其性能.双连通是网络抗毁性能的基本需求,另一方面当节点的连通度大于4时,不仅会造成网络的通信能耗过大,还会使系统运动约束增多.因此,以簇头的拓扑为3-连通为例来验证本文算法的有效性.监控区域的大小设为100 m×100 m,节点的数目为40个,节点的通信半径设为30 m,分簇个数为4,簇头的拓扑为3连通.
系统分簇及簇内拓扑邻居关系如图 5所示.利用关键节点检测算法检测到网络有2个簇存在关键节点,分别是30、38和22号节点.如果这3个关键节点遭受破坏,那么将会造成簇内网络的分割,被分割的节点之间就无法进行通信,进而造成协同控制任务的失败,所以需要对关键节点加以保护.从图 5可看出,节点号为30的关键节点的1-跳邻居节点按照极角的大小进行逆时针排序后的顺序为10、31、35、29、33.根据Haraary图的思想,需要添加新的信息交互边29-33、33-10来构建以关键节点为中心的局部3-连通拓扑结构来去除关键节点.所以需要移动29号节点让29和33号节点相互通信,移动33号节点让33和10号节点相互通信.节点号为38的关键节点的邻居节点按照极角的大小进行逆时针排序后的顺序为16、24、36、8、28、4、32,需要添加新的信息交互边8-28和32-16来构建以关键节点为中心的局部3-连通拓扑结构.同理,22号节点需要添加新的信息交互边3-15、21-3.去除关键节点后任意删除簇内的两个节点之后,网络还是连通的,增强了系统的抗毁性.

|
图 5 簇内有关键节点的拓扑图 |
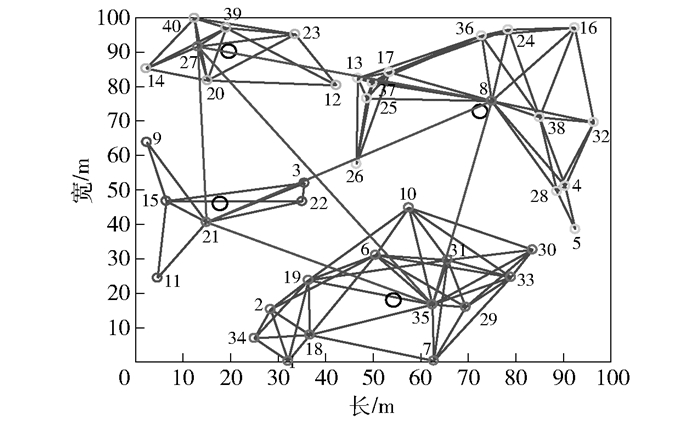
簇内去除关键节点后的网络拓扑结构如图 6所示.去除关键节点后,依据规则选举出簇头节点,其编号是27、21、35、8,簇头间的3-连通拓扑结构如图 6中所示.任意2个簇头节点失效,剩余的簇之间还是可以进行通信,可增强系统的抗毁性.
|
图 6 簇内去关键节点后且簇头k-连通的拓扑图 |
笔者利用网络的节点介数中心性、网络的平均连通度、网络的鲁棒性来对比分析每个簇内去除关键节点前后网络的抗毁性能变化.
3.1 介数中心性评价节点p的介数[13-14]Bp反映了其在整个系统中的影响力,定义为网络中所有的最短路径之中,经过节点的最短路径数占所有最短路径的比值,介数Bp的计算公式为
| $ {B_p} = \sum\limits_{(i, j)} {\frac{{{g_{ipj}}}}{{{g_{ij}}}}} (i, j \ne p, i \ne j) $ | (4) |
其中:gipj表示经过节点p的节点i、j间的最短路径的个数. Bp的值越大说明节点p在系统中的影响力和重要性越大.
网络中节点的介数中心性的计算公式为
| $ {W_p} = \frac{{2\sum\limits_{(i, j)} {\frac{{{g_{ipj}}}}{{{g_{ij}}}}} }}{{n(n - 1)}} $ | (5) |
其中:n是网络中总的节点个数,则网络中节点间的最短路径个数是n(n-1)/2.
去除关键节点前系统中节点介数中心性大小分布如图 7所示,图 7中编号为38的节点介数最大,这是因为关键节点两侧的节点进行通信都要经过关键节点,这与实际情况是相符合的.从图 5可以看出如果节点编号为30、22的关键节点失效,只会分别造成节点33和3与其所属簇的其他节点不连通,所以图 7中30和22号节点的介数小于0.005.当构建以关键节点为中心的局部3连通拓扑结构后,各节点的介数大小如图 8所示.从图 8可知,关键节点22、30和38的节点介数都有所下降,但是节点16、8、28、4、33号节点的介数也都相应增大了,这说明对关键节点进行保护之后,关键节点两侧节点进行通信时,可以通过其他节点进行转发,关键节点不再是其两侧节点进行通信的必经节点,这与实际情况是相符的.

|
图 7 簇内去关键节点前网络中节点介数中心性大小分布 |

|
图 8 簇内去关键节点后网络中节点介数中心性大小分布 |
网络鲁棒性[14]是用来衡量移除任意节点后网络中的剩余节点之间仍然能够保持连通能力的平均影响力,其定义是删除任意节点后网络中仍可连通的节点对数与网络中总的节点对数之比的均值.假设移除某个节点后,网络中剩下的节点集合是Gk,网络鲁棒性nR计算公式为
| $ {n_R} = \frac{1}{{n(n - 1)}}\sum\limits_{i \in {G_k}} {\sum\limits_{j > i} {{l_{ij}}} } $ | (6) |
其中:n表示网络中总节点数目,lij表示网络中仍连通节点的对数,如果节点i,j之间存在路径,则lij=1,否则lij=0.
3.3 平均连通度评价节点的度[14]反映了其对网络连通性影响的大小,通常是指与某个节点直接相连的边个数.则节点i的度ki的计算公式为
| $ k_{i}=\sum a_{i j} $ | (7) |
其中:如果节点i和节点j直接相连,则aij=1;否则aij=0.
网络的平均度(平均连通度)D是网络中所有节点度的平均值,D的计算公式为
| $ D = \frac{{\sum\limits_{i = 1}^n {{k_i}} }}{n} $ | (8) |
在去关键节点前和去关键节点后,网络的性能对比分析数据如表 1所示.
|
|
表 1 网络性能对比分析 |
从表 1可知,对于含有关键节点的网络:网络的平均连通度为4.9;网络的鲁棒性是删除关键节点后的鲁棒性,其值为0.186 19.对于根据去关键节点策略去关键节点后的网络:网络的平均连通度为5.4;网络的鲁棒性是删除原有关键节点后网络的鲁棒性,其值为0.262 76.因为去关键节点后网络中产生了新的信息交互边,所以网络的平均连通度提高了9.26%.网络的鲁棒性提高了29.14%,说明簇中去除关键节点后增强了网络的抗毁性.
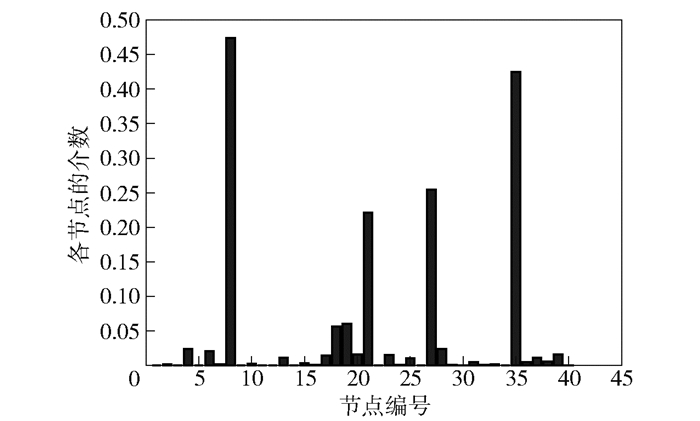
3.4 簇头拓扑构建后全网介数中心性评价在簇头拓扑构建阶段,簇头依据Harary图的规则构建3连通拓扑结构.簇头拓扑好之后,整个网络的介数大小如图 9所示.
|
图 9 簇头拓扑后网络中节点介数大小分布 |
从图 9中可以看出,簇头节点即8、21、27、35号节点的介数较大,这是因为簇间信息的传递都依靠簇头进行转发.但是在簇之间进行信息传递时,簇内节点可以进入休眠状态来提高节点能量利用率.由于在无线网络中,传递数据包时间延时主要产生在节点接收、处理以及发送数据的过程中,而当网络负载相同时,数据包的时间延迟主要与传输路径上经过的跳数有关.在图 6中,11号节点收集到的信息传达到27号节点只需经过21号簇头即可到达27号节点.但是,如果不进行分簇的话,11号节点到达27号节点的路径为11-15-9-14-27,即至少要经过4跳的距离.所以说,分簇拓扑且簇头进行k-连通的拓扑结构,不仅网络的实时性较好,而且提高了系统的抗毁性.
4 结束语对物联网智能安防系统抗毁性拓扑结构进行了研究,并针对关键节点导致的拓扑结构的脆弱性,提出了一种较强抗毁性能的层次型物联网系统拓扑构建方法.在对网络分簇的基础上,在每个簇内检测关键节点,并利用节点的移动性构建了以关键节点为中心的局部k-连通(2-连通或3-连通)拓扑结构,抽取出簇头构成簇间k-连通的骨干网络.通过仿真实验对节点的介数中心性、平均连通度和鲁棒性进行评价,结果表明笔者所提出的方法能很好地增强系统拓扑结构的抗毁性.
| [1] |
孙其博, 刘杰, 黎羴, 等. 物联网:概念、架构与关键技术研究综述[J]. 北京邮电大学学报, 2010, 33(3): 1-9. Sun Qibo, Liu Jie, Li Shan, et al. Internet of things:summarize on concepts, architecture and key technology problem[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(3): 1-9. |
| [2] |
王飞跃, 张俊. 智联网:概念、问题和平台[J]. 自动化学报, 2017, 43(12): 2061-2070. Wang Feiyue, Zhang Jun. Internet of minds:the concept, issues and platforms[J]. ACTA Automatica Sinica, 2017, 43(12): 2061-2070. |
| [3] |
陶飞, 程颖, 程江峰, 等. 数字孪生车间信息物理融合理论与技术[J]. 计算机集成制造系统, 2017, 23(8): 1603-1611. Tao Fei, Cheng Ying, Cheng Jiangfeng, et al. Theories and technologies for cyber-physical fusion in digital twin shop-floor[J]. Computer Integrated Manufacturing Systems, 2017, 23(8): 1603-1611. |
| [4] |
Mumtaz S, Alsohaily A, Pang Z, et al. Massive internet of things for industrial applications:Addressing wireless IoT connectivity challenges and ecosystem fragmentation[J]. IEEE Industrial Electronics Magazine, 2017, 11(1): 28-33. DOI:10.1109/MIE.2016.2618724 |
| [5] |
Fan X G, Yang J J, Wang H. A probabilistic overlay enhancement algorithm for wireless sensor networks[J]. Journal of Software Engineering, 2016, 27(2): 418-431. |
| [6] |
Dai G Y, Shi W Y, Ying K Z, et al. A new approach to the WSN fence based on the two deployment of mobile nodes[J]. Telecommunications Science, 2017, 33(6): 97-104. |
| [7] |
Basu P, Redi J. Movement control algorithms for realization of fault-tolerant Ad hoc robot networks[J]. IEEE Network, 2004, 18(4): 36-44. |
| [8] |
Rosset V, Paulo M A, Cespedes J G, et al. Enhancing the reliability on data delivery and energy efficiency by combining swarm intelligence and community detection in large-scale WSN[J]. Expert Systems with Application, 2017, 78(15): 89-102. |
| [9] |
Varadarajan K M, Vincze M. Mobility aware topology control framework for dynamic multi-robot networks[C]//International Conference on Methods & Models in Automation & Robotics. Miedzyzdroje: [s. n. ], 2011: 272-277.
|
| [10] |
Park H, Hutchinson S A. Fault-tolerant rendezvous of multirobot systems[J]. IEEE Transactions on Robotics, 2017, 33(3): 565-582. DOI:10.1109/TRO.2017.2658604 |
| [11] |
Wang Q, Chen J, Fang H. A localized K-connectivity topology control algorithm in multi-agent networks[C]//Control Conference (CCC). [S. l. ]: IEEE, 2012: 6315-6320.
|
| [12] |
王强, 陈杰, 方浩. 一种多智能体系统抗毁性拓扑结构构建方法[J]. 模式识别与人工智能, 2014(4): 356-362. Wang Qiang, Chen Jie, Fang Hao. A Construction method of fault-tolerant topology for multi-agent systems[J]. PR & AI, 2014(4): 356-362. DOI:10.3969/j.issn.1003-6059.2014.04.010 |
| [13] |
郭晓成, 马润年, 王刚. 复杂网络中节点重要性综合评价方法研究[J]. 计算机仿真, 2017, 34(7): 264-268. Guo Xiaocheng, Ma Runnian, Wang Gang. Research on comprehensive evaluation method of node importance in complex network[J]. Computer Simulation, 2017, 34(7): 264-268. DOI:10.3969/j.issn.1006-9348.2017.07.059 |
| [14] |
李文锋, 符修文. 无线传感器网络抗毁性[J]. 计算机学报, 2015, 38(3): 625-647. Li Wenfeng, Fu Xiuwen. Survey on invulnerability of wireless sensor networks[J]. Chinese Journal of Computers, 2015, 38(3): 625-647. |


