分析了第5代移动通信系统(5G)中超可靠低时延通信(URLLC)业务与增强移动带宽(eMBB)业务共存时,资源预留分配策略对URLLC业务的时延保障程度以及对eMBB业务服务质量的影响程度.基于随机网络演算分析理论,推导了满足URLLC业务概率时延约束要求的前提下所需的资源预留比例,即满足URLLC业务时延要求的最小门限值.此外,分析了eMBB业务的时延性能.研究结果表明,在系统总资源固定的情况下,为URLLC业务预留一定比例的资源后,eMBB业务的时延分布会受到一定程度的影响,其时延分布的恶化程度与资源预留比例密切相关.
The delay guarantee of ultra-reliable and low-latency communication (URLLC) traffic under resource reservation policy was analyzed when both URLLC traffic and enhanced mobile broadband (eMBB) traffic co-exist in the fifth generation of mobile communications system (5G) system. The impact on eMBB traffic's quality of service was also analyzed. Based on the stochastic network calculus theory, the needed resource reservation ratio for URLLC traffic with probabilistic delay constraint requirement was investigated. Specifically, a minimum threshold, meeting this delay requirement for URLLC traffic, was derived. In addition, the delay performance of eMBB traffic was also analyzed. The results showed that, when the system resource was fixed, the delay distribution of eMBB traffic would be influenced by the amount of resource reserved for URLLC traffic, and the deteriorate level greatly depended on the reservation ratio.
第5代移动通信系统(5G, the fifth generation of mobile communications system)将渗透到未来生活的各个方面,为未来全球的信息化建设提供坚实的基础[1-2].因此,针对5G的标准化进程以及关键技术的研究显得尤为重要.从信息交互对象不同的角度,5G系统将涵盖以下3大场景[1-2]:增强移动带宽(eMBB, enhanced mobile broadband)、超可靠低时延通信(URLLC, ultra-reliable and low-latency communication)和海量机器类通信.这3类场景所针对的具体应用场合不同、业务特点不同,对5G网络提出的技术需求也不同.当多种业务在5G网络中共存时,如何在业务之间进行资源分配和复用,进而满足各业务的技术指标,就成为5G网络必须解决的关键问题之一.其中,eMBB业务与URLLC业务预计在5G中期(即2021—2022年)发展成熟,因此,针对eMBB和URLLC的复用技术研究是近些年的研究重点. eMBB业务是未来5G网络中的基础业务,占据主导地位,其特点是数据量大,对传输速率的要求较高.相比之下,URLLC业务的数据包较小,对时延和错误率的要求都很严格.因此,在已有eMBB业务的前提下,如何对资源进行合理分配,进而能够保证URLLC业务的服务质量要求是一个亟待解决的问题.
目前已有的研究可以分为2个方面:标准化研究和学术研究.标准化研究是以提案的形式给出,重点关注URLLC/eMBB帧结构设计[3-4]、URLLC与eMBB业务复用机制[5-6]、仿真参数配置[7]等系统实现相关的内容,部分提案给出了针对错误率的仿真结果[6-8].学术研究以论文的形式给出,通常以特定场景和具体算法实现为落脚点,如干扰协调问题[9]、用于增强URLLC业务的安全性和可靠性的正交频分复用子载波索引选择技术[10]、存在大量、突发性URLLC数据包时的业务检测和冲突避免技术[11-12]、链路自适应与资源调度的联合算法[13]等.已有研究缺少一般性理论建模,未能针对URLLC业务的时延特性进行深入探讨.基于此,笔者依托随机网络演算理论,建立用于描述URLLC业务和eMBB业务复用场景的通用模型,通过分析概率时延分布情况,从理论上推导保证URLLC业务时延要求的资源预留边界,为系统设计及性能优化提供理论依据.
笔者研究了资源预留模式下URLLC业务和eMBB业务的资源分配占比,通过定义时延受限吞吐量将URLLC业务的时延和错误率进行联合考虑.利用最小加代数和网络演算分析方法,推导满足一定概率时延约束条件下,系统需要为URLLC业务预留资源的下界,同时分析资源预留为eMBB业务带来的性能损失.
1 系统模型如图 1所示的移动通信系统,eMBB业务和URLLC业务以资源预留的方式共享系统资源,其中预留给URLLC业务的资源占比为η,预留给eMBB业务的资源占比为1-η. eMBB业务和URLLC业务的数据包均依据泊松过程到达系统,到达强度分别为λe和λu,数据包的大小分别为Le和Lu.

|
图 1 系统模型 |
文中所提及的时延定义为从数据包产生到数据包被传输结束的时间差.当数据包经历的时延大于可容忍的最大时延时,该包将被丢弃.被丢弃的数据包,对于接收端而言,即视为一次错误接收.虽然实际系统接收端的错误接收既包含丢包造成的错误,也包含由于信道条件等原因导致的接收失败引起的错误[14-15],但是文中所提及的错误率只考虑丢包引入的接收失败.在此基础上,定义概率时延约束实现对时延和错误率的联合考虑.
定义1 概率时延约束.若业务可容忍的最大错误率为ε,其数据包可容忍的最大时延为d,数据包所经历的实际时延为D(t),则概率时延约束定义为
| $ P{D(t)>d}≤ε $ | (1) |
当URLLC业务与eMBB业务以资源预留模式复用时,预留资源占比η越大,则对URLLC业务的服务质量保证越好,但是对eMBB业务的影响也最大.因此,资源预留所需解决的根本问题是:找到最小的资源预留占比η,在保证URLLC业务的概率时延约束的前提下,将对eMBB业务的影响降到最小.令Du(t)、du和εu分别表示URLLC数据包的实际时延、可容忍的最大时延和可容忍的最大错误率,则资源预留方案的最优化问题可以归结为
| $ \begin{array}{l}{\min \eta} \\ {\text { s.t. } P\left\{D_{\mathrm{u}}(t)>d_{\mathrm{u}}\right\} \leqslant \varepsilon_{\mathrm{u}}}\end{array} $ | (2) |
在分析业务可以获得的服务质量保证之前,首先需要完成对业务特性以及网络服务能力的数学描述.笔者基于最小加代数理论和随机网络演算理论所定义的随机到达曲线和随机服务曲线,完成所需服务质量保证的分析.
网络演算理论是用于分析网络中流问题的一种方法[16],自1991年提出以来,已逐渐演进为2个分支:确定性网络演算[17]和随机网络演算[18].本项目研究的是随机性较强的无线网络问题,依托随机网络演算理论进行.
随机网络演算的系统模型如图 2所示,包括随机到达曲线A(t)~〈α, f〉、随机服务曲线S(t)~〈β, g〉以及输出数据流A*(t)3个部分.在获得随机到达曲线和随机服务曲线的具体数学描述的基础上,即可实现对输出数据流的特性分析.

|
图 2 随机网络演算系统模型 |
随机到达曲线由定义在累积数据量基础上的一个关于时间的函数和一个关于数据量的边界函数构成.
定义2 随机到达曲线.令A(s, t)表示业务流A在时间段(s, t]内累积到达系统的数据量,若∀t≥0和∀x≥0,函数α(t)和函数f(x)满足
| $ P\left\{\sup\limits_{0 \leqslant s \leqslant t}\{A(s, t)-\alpha(t-s)\}>x\right\} \leqslant f(x) $ | (3) |
则称函数α(t)和函数f(x)为业务流A的随机到达曲线,记为A(t)~〈α, f〉,其中A(t)=A(0, t),sup {·}表示上确界.
与随机到达曲线的概念类似,随机服务曲线由一组用于描述服务能力的函数对构成,定义如下.
定义3 随机服务曲线.令A*(t)表示在时间段(0, t]内累积输出服务器S的数据量,若∀t≥0和∀x≥0,函数β(t)和函数g(x)满足
| $ P\left\{A \otimes \beta(t)-A^{*}(t)>x\right\} \leqslant g(x) $ | (4) |
则称函数β(t)和函数g(x)为服务器S的随机服务曲线,记为S(t)~〈β, g〉,其中A⊗β(t)≡
在已知业务流的到达特性和服务器的服务特性的前提下,利用最小加代数理论可以获得时延的概率分布的上界.下面直接将相关结论总结在定理1中,详细的推导请参见文献[18].
定理1 时延分布上界.考虑服务器S为数据流A提供数据传输.若已知数据流A的随机到达曲线是A(t)~〈α, f〉,服务器S的随机服务曲线是S(t)~〈β, g〉,则∀t≥0和∀x≥0,在t时刻产生的数据包的时延D(t)=inf {τ≥0:A(t)≤A*(t+τ)}的分布受限于
| $ P\{ D(t) \ge h(\alpha + x, \beta )\} \le f \otimes g(x) $ | (5) |
其中h(α+x, β)表示函数α(t)+x与函数β(t)之间的最大水平距离,可以进一步写为
| $ h(\alpha + x, \beta ) = \mathop {\sup }\limits_{t≥0} \{ \inf \{ \tau \ge 0:\alpha (t) + x \le \beta (t + \tau )\} \} $ | (6) |
考虑如图 1所示的移动通信系统,将其中各部分所对应的随机网络演算描述引入后,如图 3所示.

|
图 3 系统模型的随机网络演算描述 |
设系统可以提供的平均传输速率为R,则系统的随机服务曲线可以表示为S~〈β(t)=Rt, g(x)=0〉.考虑资源预留后,URLLC业务和eMBB业务可以真正获得的服务能力分别为
| $ S_{\mathrm{u}} \sim\left\langle\beta_{\mathrm{u}}(t)=\eta R t, g_{\mathrm{u}}(x)=0\right\rangle $ | (7) |
| $ S_{\mathrm{e}} \sim\left\langle\beta_{\mathrm{e}}(t)=(1-\eta) R t, g_{\mathrm{e}}(x)=0\right\rangle $ | (8) |
泊松过程是用于描述业务到达特性的一种典型类型,在通信系统建模中被广泛使用.在泊松过程中,2个数据包到达系统的时间间隔呈负指数分布,时间间隔的均值为1/λ,即单位时间内到达系统的数据包的平均个数为λ,称为到达率. URLLC业务和eMBB业务均可以用泊松到达过程来模拟.已知泊松到达过程的随机到达曲线如下[6].
定义4 泊松到达过程的随机到达曲线.设业务流的所有数据包的长度L均相同,并且数据包依据泊松过程到达系统,到达率为λ,对于任意的r>λL,随机到达曲线可以表示为
| $ \left. {\begin{array}{*{20}{l}} {\alpha (t) = rt}\\ {f(x) = 1 - (1 - a)\sum\limits_{i = 0}^k {\left[ {\frac{{{{[a(i - k)]}^i}}}{{i!}}{{\rm{e}}^{ - a(i - k)}}} \right]} } \end{array}} \right\} $ | (9) |
其中:a=λL/r,k=⌈x/L⌉.
用Au~〈αu, fu〉表示URLLC业务的随机到达曲线,αu(t)=rut,则依据定理1,可以获得URLLC业务的时延分布上界为
| $ P\left\{D_{\mathrm{u}}(t) \geqslant \frac{x}{\eta R}\right\} \leqslant f_{\mathrm{u}}(x) $ | (10) |
若URLLC数据包可容忍的最大时延为du、业务可容忍的最大错误率为εu,则可知
| $ P\left\{D_{\mathrm{u}}(t) \geqslant d_{\mathrm{u}}\right\} \leqslant f_{\mathrm{u}}\left(\eta R d_{\mathrm{u}}\right)=\varepsilon_{\mathrm{u}} $ | (11) |
当系统平均服务速率给定时,保证URLLC业务概率时延约束的最小资源预留占比为
| $ \eta_{\min }=\frac{f_{\mathrm{u}}^{-1}\left(\varepsilon_{\mathrm{u}}\right)}{R d_{\mathrm{u}}} $ | (12) |
当系统中所有资源可供eMBB业务使用时,依据定理1可知eMBB数据包的时延分布上界为
| $ P\left\{ {{D_{\rm{e}}}(t) \ge \frac{x}{R}} \right\} \le {f_{\rm{e}}}(x) $ | (13) |
即
| $ P\left\{D_{\mathrm{e}}(t) \geqslant d_{\mathrm{e}}\right\} \leqslant f_{\mathrm{e}}\left(R d_{\mathrm{e}}\right) $ | (14) |
假设eMBB数据包的长度为Le,以泊松过程到达,强度为λe,随机到达曲线为Ae~〈αe, fe〉,αe(t)=ret.
当系统为URLLC业务预留资源时,eMBB业务的实际可用资源由原来的R缩减为(1-η)R,因此,其概率时延分布的上界会恶化为
| $ P\left\{D_{\mathrm{e}}(t) \geqslant d_{\mathrm{e}}\right\} \leqslant f_{\mathrm{e}}\left((1-\eta) R d_{\mathrm{e}}\right) $ | (15) |
参考5G相关的仿真结果[19],设定系统空中接口部分的无线传输平均速率为20 Mbit/s.结合URLLC业务和eMBB业务的特征[19-20],确定URLLC业务的数据包长度为32 B,概率时延约束为(1 ms, 10-5),eMBB业务的数据包长度为0.5 MB,数据包到达率为2 pkt/s.
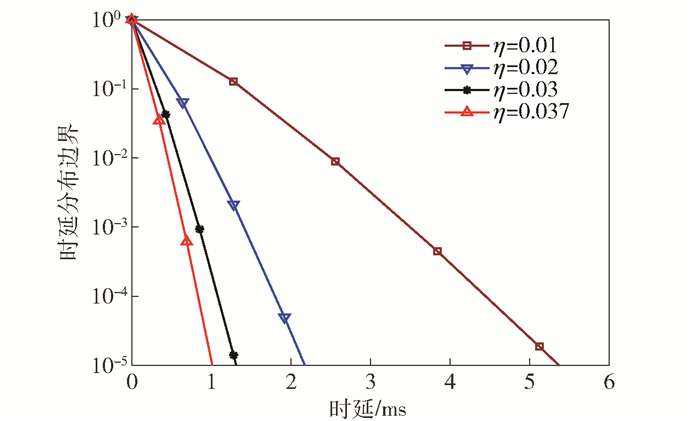
图 4给出了固定URLLC业务数据包到达率λv为100 pkt/s时,不同资源预留比例下的概率时延分布结果.从图 4中可以看出,随着资源预留比例的增加,URLLC业务的概率时延保障越好.当资源预留比例达到3.7%时,URLLC业务数据包时延超过1 ms的概率不超过10-5,满足其概率时延约束,即在此配置下,系统资源预留比例应不小于3.7%.
|
图 4 URLLC业务的概率时延分布 |
图 5给出了上述条件下,不同的资源预留比例对eMBB业务的概率时延分布的影响.从图 5中可以看出,随着资源预留比例的增加,eMBB业务的时延会变大.但是由于eMBB业务数据包本身较大,当资源预留比例相对较小时,eMBB业务的时延恶化并不明显.当URLLC业务的到达率增大时,最小资源预留比例也应当随之增长. 表 1给出了URLLC业务不同到达率配置下,资源预留比例.

|
图 5 eMBB业务的概率时延分布 |
|
|
表 1 资源预留下界 |
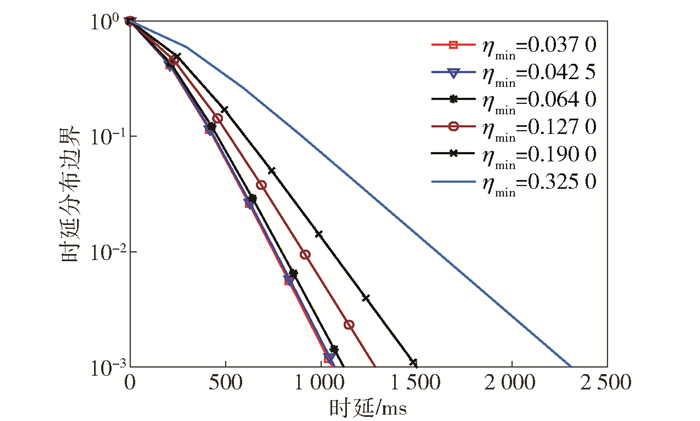
随着预留给URLLC业务的资源量增加,eMBB业务可使用的资源减少,当减少量较多时,其时延性能会明显恶化. 图 6给出了表 1中各资源预留比例对应的eMBB业务的概率时延分布.从图 6中可以看出,当ηmin较小时,时延的恶化并不明显;当ηmin由12.7%增大到19%以及32.5%时,概率时延分布曲线显著右移.例如,当ηmin为12.7%时,eMBB业务数据包时延超过1 000 ms的概率不大于10-2;当ηmin为32.5%时,eMBB业务数据包时延超过1 000 ms的概率接近10-1.
|
图 6 表 1对应的eMBB业务的概率时延分布 |
eMBB业务与URLLC业务在系统中共存是未来5G通信系统的典型场景.由于两类业务的生成特性不同、服务质量要求不同,也就对网络的服务特性提出了挑战.资源预留作为一种解决方案,其中所涉及的资源预留比例需要进行合理的配置,才能更好地保障两类业务的服务质量需要.笔者基于随机网络演算分析,构建了eMBB与URLLC业务复用的通用模型,推导了满足URLLC业务概率时延约束的资源预留比例的下界,也分析了资源预留为eMBB业务带来的性能损失.研究结果表明,当URLLC业务的数据量较多时,资源预留模式下,eMBB业务的时延性能会显著恶化.研究结果为系统设计及资源分配提供了理论依据,资源预留下界的确定,能够在满足URLLC业务服务质量保证需求的前提下,将对eMBB业务性能的损失降至最低.
| [1] |
朱红梅, 林奕琳, 刘洁. 5G URLLC标准、关键技术及网络架构的研究[J]. 移动通信, 2017(17): 28-33. Zhu Hongmei, Lin Yilin, Liu Jie. Research on URLLC standard, key technique and network architecture for 5G[J]. Mobile Communications, 2017(17): 28-33. DOI:10.3969/j.issn.1006-1010.2017.17.006 |
| [2] |
温萍萍. 5G网络中支持URLLC业务的数据复制传输技术[J]. 无线互联科技, 2018(10): 20-22. Wen Pingping. Data duplication technique supporting URLLC service in 5G network[J]. Wireless Internet Technology, 2018(10): 20-22. DOI:10.3969/j.issn.1672-6944.2018.10.010 |
| [3] |
3GPP R1-167127. Frame structure considerations for URLLC[R].[S.l.]: Intel Corporation, 2016.
|
| [4] |
3GPP R1-1608957. URLLC and eMBB frame structure and multiplexing[R].[S.l.]: ZTE Microelectronics, 2016.
|
| [5] |
3GPP R1-1611222. DL URLLC multiplexing considerations[R].[S.l.]: Huawei HiSilicon, 2016.
|
| [6] |
3GPP R1-1704215. On pre-emption indication for DL multiplexing of URLLC and eMBB[R].[S.l.]: Huawei HiSilicon, 2017.
|
| [7] |
3GPP R1-166398. URLLC system level simulation assumptions[R].[S.l.]: Qualcomm Incorporated, 2016.
|
| [8] |
3GPP R1-1609057. Evaluation results of eMBB with HARQ retransmission in case of multiplexing eMBB and URLLC[R].[S.l.]: Samsung, 2016.
|
| [9] |
Abreu R, Berardinelli G, Jacobsen T, et al. A blind retransmission scheme for rltra-reliable and low latency communications[C]//2018 IEEE 87th Vehicular Technology Conference. Porto: IEEE, 2018: 1-5.
|
| [10] |
Singh B, Tirkkonen O, Li Z, et al. Interference coordination in rltra-reliable and low latency communication networks[C]//2018 European Conference on Networks and Communications. Ljubljana, Slovenia: IEEE, 2018: 251-255.
|
| [11] |
Jehad M, Hamamereh, Ertugrul Basar, et al. OFDM-subcarrier index selection for enhancing security and reliability of 5G URLLC services[J]. IEEE Access, 2017(5): 25863-25875. |
| [12] |
Jacobsen Thomas, Abreu Renato, Berardinelli Gilberto, et al. System level analysis of uplink grant-free transmission for URLLC[C]//2017 IEEE Globecom Workshops. Singapore: IEEE, 2017: 1-6.
|
| [13] |
Pocovi G, Pedersen K I, Mogensen P. Joint link adaptation and scheduling for 5G ultra-reliable low-latency communications[J]. IEEE Access, 2018(6): 28912-28922. |
| [14] |
Zhang Yan, Jiang Yuming. Performance of data transmission over a Gaussian channel with dispersion[C]//2012 International Symposium on Wireless Communication Systems. Paris, France: IEEE, 2012: 721-725.
|
| [15] |
Fu Songwei, Zhang Yan, Ceriotti Matteo, et al. Modeling packet loss rate of IEEE 802.15.4 links in diverse environmental conditions[C]//2018 IEEE Wireless Communications and Networking Conference. Barcelona, Spain: IEEE, 2018: 1-6.
|
| [16] |
Cruz R L. A calculus for network delay:part Ⅰ:network elements in isolation and part Ⅱ:network analysis[J]. IEEE Transactions on Information Theory, 1991, 37(1): 114-141. DOI:10.1109/18.61109 |
| [17] |
Boudec J-Y Le, Thiran P. Network calculus:atheory of deterministic queuing systems for the internet[M]. Berlin Heidelberg: Springer, 2001: 1-274.
|
| [18] |
Jiang Y, Liu Y. Stochastic network calculus[M]. London: Springer-Verlag, 2008: 1-207.
|
| [19] |
3GPP R1-1611222. DL URLLC multiplexing considerations[R].[S.l.]: Huawei HiSilicon, 2016.
|
| [20] |
3GPP R1-167127. Frame structure considerations for URLLC[R].[S.l.]: Intel Corporation, 2016.
|


