极化码是第五代移动通信(5G)的重要信道编码,是被用于增强移动宽带场景控制信道的纠错编码.TS 38.212协议规定的5G-Polar码存在3种码字结构,但没有给出设计的原因和对应的译码方法.为此,介绍了5G-Polar码的可靠性序列设计方法和速率匹配方法,并分析了不同类型的码字构造原理、关键特征及相应的译码算法.通过对不同结构类型Polar码的性能和复杂度的对比,分析了各种结构类型的适用条件及原因.同时,通过仿真定量地给出了5G-Polar码在短码条件下相比于LTE TBCC和5G-LDPC码的性能优势.
Polar codes are important channel coding for the fifth generation mobile communication (5G), which are already used for control channels for enhance mobile broadband (eMBB) scenarios. At present, the 5G-polar codes specified in the 3GPP TS 38.212 standard have three code structures, but the design reasons and corresponding decoding methods have not been given yet. Firstly, the reliability sequence design and rate-matching method are introduced, and then the principle, the key feature and the decoding algorithm of every code structure are analyzed. Through the performance and complexity comparison analysis of three kinds of polar codes, the applicable condition and reason for each code structure are detailed. At the same time, the performance advantages of the short-size 5G-polar codes over LTE TBCC and 5G-LDPC codes are given quantitatively by computer simulations.
早在1960年,Plotkin[1]就已经证明|u, u+v|形式的递归编码可以构造具有指定最小汉明距离的二进制编码.这种编码方法被用于Reed-Muller(RM)码的构造. Arikan[2]在此基础上进行了更为深入的研究,发现这种递归编码的方式可以使一组独立的离散无记忆信道呈现不同的可靠性.随着信道数目的增加,各个比特信道的可靠性逐渐趋于两极分化,即信道极化现象.以信道极化为依托,Arikan提出了极化码(polar codes)的最初模型.在码字构造上Polar码沿用了RM码的递归形式,采用G2=
Polar码的结构中,除了承载信息比特的信息信道以外,还存在一种承载固定比特的“冻结信道”.基于这种特殊的码字设计,Arikan提出了一种低复杂度(O(NlbN))的译码算法——串行抵消(SC,successive cancellation)译码.由于冻结信道的信息是固定的,提高了译码的可靠性.虽然Arikan在理论上证明了在无限码长的情况下Polar码是容量可达的,此时误块率可以小于2-Nβ (β < 0.5),然而在有限码长下SC算法的译码性能并不够理想. Korada等[4]研究了核矩阵的大小对Polar码性能的影响,从理论上证明了可以通过增大核矩阵来使Polar码的误码率随码长增加呈负指数下降,并利用BCH码构造了指数β接近于1的核矩阵. Tal和Chen Kai等[5-6]通过SC译码的码树分析,提出了增强型的译码算法——串行抵消列表译码(SCL,successive cancellation list)算法. SCL译码在付出一定译码复杂度代价的情况下获得了非常接近最大似然译码的性能.但是,路径度量大的序列并不一定是真正的译码结果,Tal[7-8]在SCL译码的基础上用CRC (cyclic redundancy check)校验来检测候选路径的正确性,提出了CRC辅助的SCL译码算法(CA-SCL,CRC aid successive cancellation list)进一步提高了polar码的译码性能. Li Bin等[9]指出Tal的CA-SCL译码方案需要很大的列表宽度才能逼近最大似然译码的性能,提出了一种渐进增大列表宽度的CRC辅助译码方案,降低了译码复杂度.
目前,在第五代移动通信(5G,fifth generation mobile communication)增强移动宽带(eMBB,enhance mobile broadband)场景控制信道中,polar码代替了咬尾卷积码(TBCC,tail biting convolution code)成为主要编码方案[10]. TS 38.212协议(以下简称“协议”)[11]已经规定了Polar码的编码流程,在上/下行信道采用了不同的编码结构.但是,协议没有给出采用这种编码方案的原因和对应的译码方法.
针对协议中未涉及的内容,主要有以下贡献:1)结合3GPP提案和协议介绍了Polar码的3种结构类型,详细分析了每种码字构造的基本原理、关键特征和译码算法. 2)通过性能仿真和复杂度的比较分析,解释了协议中采用3种Polar码结构的应用条件及原因,并通过仿真定量的给出了5G-Polar码在短码条件下相比于LTE TBCC和5G-LDPC码的性能优势,指明了未来5G系统中Polar研究的若干开放性关键问题.
1 比特信道的可靠性序列设计Polar码利用信道极化现象进行编码,然而如何衡量每个比特信道的可靠性则是关键问题. Arikan[2]最初提出的衡量准则是Bhattacharyya系数,给出了该参数在二进制删余信道(BEC,binary eliminated channel)下的递归计算公式,对于AWGN (additive white Gaussian noise)等信道则建议可以采用仿真的方式统计每个比特信道的差错概率.显然,仿真的计算量大,时间复杂度随码长指数增加.为了减少时间复杂度,出现了密度进化(DE,density evolution)和高斯近似(GA,Gaussian approximation)等算法. Mori等[12-13]基于密度进化的思想,在BSC (binary symmetric channel)、AWGN信道下给出了更好的子信道选择标准.根据密度进化原理,需要对因子图上各个消息节点的概率密度函数进行卷积计算.在具体实现时需要采用高维向量来存储量化后的概率密度函数以确保计算精确性,导致计算输出的维度随码长呈指数增长,因而具有较高复杂度.基于信道极化,Tal等[14]把参与密度进化计算的各个比特信道近似为具有有限输出维度的等效信道,从而降低了计算复杂度.另外,密度进化也存在量化误差,为了获得更精准的错误概率预测,Trifonov等[15-16]利用AWGN信道下的输出似然值近似服从正态分布这一特点,运用高斯近似的方法解决了密度进化带来的量化误差.
在此基础上,华为公司[17]提出了一种基于高斯近似的密度进化(DE/GA)设计方案,这是密度进化的近似版本.该方案与速率匹配方式相互影响,所以在设计时可靠性序列和速率匹配方式需要一一对应.为了支持更广泛的码长、码率、信噪比和多样化的速率匹配方式,华为公司[18]又提出了通过计算比特信道的极化权重(PW,polarization weight)获得可靠性序列的方法.每个比特信道的极化权重只与索引号有关,权重越大,对应的子信道越可靠.因此是一种“独立于信噪比”的估计算法.文献[19]表明,极化权重法与DE/GA算法相比,能够减少75%的空间复杂度.但是,极化码源于信道极化,与信道特性密切相关,极化权重法相比于DE/GA算法有0.2 dB的性能损失.
高通公司在文献[20]中提出的FRANK构造法从互信息的角度来衡量极化信道的可靠性,构造了一个短码长(如Nref=64)的可靠性序列Q0Nref,然后利用嵌套的方法进行编码.要获得一个长度N=2n(N>Nref)的母码,只需要把码字分为N/Nref组,然后根据信息比特数K和码率R递归计算每个分组中分配到的信息比特数Ki,最后根据Q0Nref把信息比特放置在最可靠的索引位.这种构造方法可以很容易地考虑到凿孔、缩短和重复等操作带来的影响,有助于速率匹配方案的设计.
Blasco-Serrano等[21]指出在相同的信道条件下,当码长趋于无限长时,可靠性序列是嵌套的.基于该理论,DOCOMO公司[22]进一步证明了短码长的可靠性序列可以由其长码长的母码可靠性序列得到.在设计可靠性序列时,一般用DE/GA算法估计每个比特信道的均值作为可靠性的度量,DOCOMO公司和三星公司[22-23]在给3GPP的提案中都采用了这种方法.因此,对于有限长度的Polar码只需要一个长度为Nmax的可靠性序列即可满足任意长度N≤Nmax的编码需要.具体做法是,在长度为Nmax的可靠性序列QNmax中选择索引号i < N的元素即可获得长度为N≤Nmax的可靠性序列QN,TS 38.212协议中正是采用了这样的操作.
2 速率匹配Polar码的递归构造决定了码字的长度是2的幂次,需要对其进行速率匹配才能符合实际系统的要求.一般的速率匹配方法有3种——重复、凿孔和缩短. Wang Runxin等[24]提出了一种以只对冻结位凿孔为准则的速率匹配方法,即缩短方式.从理论上证明了第i个比特信道要作为凿孔位必须满足Q(gi)∈F,其中gi是生成矩阵中的第i列,Q(gi)是非0元素的位置,F是冻结位集合. Zhang Liang和Zhang Zhaoyang等[25]以最小化错误概率为标准,通过高斯近似的方法分析不同凿孔图样带来的错误概率,从而选择最佳的凿孔图样,这也是一种对冻结位凿孔的方法.在3GPP的提案中给出了3类速率匹配方式:基于比特可靠性的速率匹配、比特翻转的速率匹配和自然速率匹配[26-27],其中讨论最多的是比特翻转和自然速率匹配.
2.1 比特翻转速率匹配华为公司在文献[28]中给出了比特翻转速率匹配的编码方案.如果母码长度为N,实际码长为M,只需要对母码最后N-M个索引[M, …N-3, N-2, N-1]进行比特翻转,即可获得缩短(Shortening)位置图样集合P.编码时把P对应的子信道作为冻结信道的一部分. Runxin Wang等[24]对这种设计方法进行了理论分析和证明.由于编码后P对应的比特均为“0”,因此输入译码器的似然比/对数似然比序列需要按P对应的位置插入极大值.
2.2 自然速率匹配自然速率匹配分为3种类型:Type-Ⅰ、Type-Ⅱ和分裂自然速率匹配.如果母码长度为N,实际码长为M,则凿孔数目为N′=N-M.
自然速率匹配的基本思想是按照比特信道的索引号依次连续的选取N′个比特信道作为凿孔图样. Type-Ⅰ的选取顺序是升序,对应的是凿孔方案,在解速率匹配时凿孔位需要补“0”;Type-Ⅱ则是依照降序选择,对应的是缩短方案.分裂自然速率匹配在凿孔数目小于或等于N/4时和Type-Ⅰ型自然速率匹配完全一致,否则剩余的凿孔位分别以N/4和N/2为起点依次选取.
爱立信公司在文献[26]中描述了各种速率匹配方案在不同码长码率条件下的性能差异,指出速率匹配的性能与码率条件有关. TS 38.212协议优化了自然速率匹配,在码率小于7/16时采用Type-Ⅰ型(凿孔),码率大于7/16时采用Type-Ⅱ型(缩短),在输出比特数大于母码长度时采用重复.
3 5G控制信道的Polar码结构设计最初提出的列表译码是通过比较候选路径的度量值来判断最终的输出结果.然而,度量值最大的路径并不一定是正确的结果.因此产生了级联检错码来提高译码可靠性的思想.从Polar码的诞生到5G的研究进程,已提出了多种“辅助比特+基本Polar”的设计方案.由于辅助比特的类型和添加方式不同,输入基本Polar编码器的信息序列和校验比特在结构上有着明显的区别.本节主要介绍3种典型的Polar码结构——集中式CRC校验的Polar码(CA-Polar)、分布式CRC-Polar码和奇偶校验(PC,parity check)-CRC联合辅助译码的Polar码(PC-CA-Polar).
3.1 集中式CRC校验的Polar码Tal等[7-8]根据CRC校验进行路径选择的思想提出了CRC辅助译码的SCL算法(CA-SCL). CA-Polar码字结构如图 1所示.从图 1可以看出,这种码字结构是在信息比特ai后级联CRC校验比特ci,是系统码,是一种集中式CRC的设计方案.首先,根据SCL算法从根节点出发进行路径延伸,把每条路径对应的后验概率作为度量值.译码过程中,如果延伸路径超过规定的数量列表宽度(L),则保留具有最大度量值的L条继续参与译码.在所有的“非冻结比特”完成译码后,在L条候选路径中选择能通过CRC校验并且度量值最高的作为最后的译码结果.

|
图 1 CA-Polar码字结构 |
高通公司[29]在此基础上对码字结构做了进一步完善,增加(或者选择)J1个CRC校验比特用于检错(也用于译码路径选择),而其余J个CRC比特用于路径选择,被称为CA-Polar,依然是集中式的设计.若译码树保留的路径数为L,用于检错的校验比特数为J1=lbL.
3.2 分布式CRC-Polar码由于极化码存在错误传播特性,之前的比特译码错误,后续的比特译码均会发生错误,继续译码会带来不必要的译码延时.
诺基亚公司和阿尔卡特朗讯公司[30-31]通过分析CRC校验比特与信息比特的关系,提出了分布式CRC辅助校验的Polar码结构. CRC校验的系统码生成矩阵G,如式(1)所示,包括系统部分I和校验部分G′.
| $ \mathit{\boldsymbol{G = }}\left( {\begin{array}{*{20}{c}} 1& \cdots &0&{{g_{0,0}}}& \cdots &{{g_{0,r - 1}}}\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0& \cdots &1&{{g_{k - 1,0}}}& \cdots &{{g_{k - 1,r - 1}}} \end{array}} \right) $ | (1) |
其中gi, j∈{0, 1}所在的行索引表示了与第j个CRC校验比特相关联的信息比特.显然每个校验比特仅与部分信息比特有关.因此,可以将校验比特分布到码字的任意位置均可实现校验.
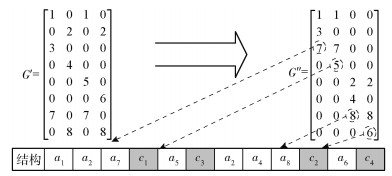
分布式CRC校验的基本做法是经过行列交换把校验部分G′转化为上三角阵G″.行列交换并不会改变信息序列与校验比特的校验关系,仅改变了信息序列和校验比特的排列次序. 图 2给出了分布式CRC校验构造方法,生成多项式为g(x)=x4+x2+1. G′和G″的非零元素表示行索引,且该位置上的值为“1”.列交换使校验比特cj产生交织{c1, c2, c3, c4}→{c1, c3, c2, c4},而行交换使信息序列ai产生交织{a1, a2, a3, a4, a5, a6, a7, a8}→{a1, a3, a7, a5, a2, a4, a8, a6}.因此,在完成译码后需要进行解交织.
|
图 2 分布式CRC-Polar码字结构 |
由此,分布式CRC-Polar码的编码过程可以描述为:先得到CRC校验的系统码,经过交织后再进行基本Polar码编码[32].码字设计的重点则体现为CRC生成多项式和交织序列的设计[33-38].
译码时,一旦遇到CRC校验比特即可对当前路径中已经译出的信息比特进行校验,只要存在1条校验成功的路径,则所有路径都保留并参与后续译码.如果所有的候选路径都校验失败,则停止后续的译码过程.这种提前终止的译码方法,在保证译码可靠性的基础上,一定程度上降低了译码的计算复杂度,减少了译码延时.
由于下行信道控制信息(DCI)有多种格式,但用户终端(UE,user terminal)事先并不知道接收到的物理下行控制信道(PDCCH,physical downlink control channel)携带的是哪种格式的DCI,也不知道该DCI使用哪个候选PDCCH进行传输,因此,PDCCH需要盲检测.如果UE检测到没有一个候选对象满足分布式的CRC检测,则UE可以提前终止解码.分布式CRC-Polar码的译码方法正好满足下行信道的盲检测需要.
3.3 基于奇偶校验的Polar码CRC辅助校验的Polar码在译码的中间过程依然只是通过路径度量值选择候选路径,并没有任何的辅助措施保证所选路径的可靠性,很有可能在路径筛选的时候修剪掉正确的路径. Wang等[39]提出在信息序列中插入Fp个PC比特,用于SCL译码路径的选择.译码时,只有满足奇偶校验关系的路径可以继续译码.在短码长和低码率情况下误码性能优于CRC辅助校验的Polar码.尽管该文献给出了PC-Polar的构造思想,但由于比特信道的错误概率是通过蒙特卡罗仿真在特定的信噪比下得到,使得码字的构造计算复杂度高且鲁棒性差.为简化码字的构造,DOCOMO公司[40]和华为公司分别提出了分布式简单奇偶校验Polar码(simple PC-Polar)和奇偶校验与CRC联合辅助译码的Polar码(PC-CA-Polar). DOCOMO的方案均匀的放置PC比特使虚警率过高,并且过于简单的奇偶校验函数更容易影响错误检测能力[41].
华为公司的方案通过选择PC比特的位置优化了候选序列的最小距离获得良好的性能.该方案的基本思想是在“信息信道”中选择具有“最小行重”的子信道作为奇偶校验位,称为PC冻结信道[42].华为公司提出了两种结构,第1种是在CA-Polar的编码结构上增加分布式的PC比特用于对译码树的修剪,并使用集中式CRC校验来对最终的译码路径进行选择[43].第2种方案借鉴分布式CRC-Polar的设计方法,为PC-CA-Polar提供提前终止译码的功能[44].事实上,在TS 38.212中PC-CA-Polar被采纳的结构形式是第1种.
码字结构中存在3种比特:1) K个信息比特ai;2) J个CRC校验比特ci;3) Fp个PC比特pi.译码时,如果遇到PC比特,则通过PC校验进行候选路径的优化,否则依然采用路径度量值进行保留路径的剪切.最后,通过CRC校验完成输出信息序列的选择. PC校验的设计关键在于确定PC比特的位置和奇偶校验关系.华为公司设计了多个版本的位置确定方法,在这里仅介绍TS 38. 212协议中的计算规则.
由于Polar码的每个比特信道都对应生成矩阵GN中的一行,可以确定最可靠的K+J个比特信道对应行具有的最小行重wmin.
从信息信道中选择Fp-n个可靠性最低的和n个行重为wmin的可靠性最高的信道索引作为冻结信道集合Pf的元素.式(2)给出了n的取值,其中M是实际码长.
| $ n = \left\{ \begin{array}{l} 1,\;\;M - K - J + 3 > 192\\ 0,\;\;M - K - J + 3 \le 192 \end{array} \right. $ | (2) |
图 3所示为K=8,Fp=3,J=4,码率1/4的码字结构.共存在M=32个子信道,信息比特和所有的校验比特占用了15个可靠性(极化权重)最大的子信道,对应的最小行重wmin=8.按构造规则选择子信道Pf={12, 14, 20}作为PC冻结信道.

|
图 3 PC-CA-Polar码字结构 |
奇偶校验关系采用记忆长度q=5的循环移位寄存器实现,先把寄存器循环左移一位,若当前输入比特是信息位ai时设置寄存器首位y[0]=y[0]⊕ai,若当前是奇偶校验位时则输出校验值pj=y[0].可见,如果PC比特之前没有信息比特输入,PC比特等效为冻结比特“0”,如图 3中的p1和p2.这是一种低复杂度的实现,但又克服了信息比特与校验比特约束关系过于简单的问题.
4 TS 38.212协议中的Polar码5G信道编码标准——TS 38.212协议给出了Polar码的编码方案[11].
可靠性序列方面,按照嵌套规则设计了一个长度为Nmax=1 024的可靠性序列QNmax.对于任意编码长度为N的码块,只需从QNmax中选择取值小于N的元素即可获得对应的可靠性序列QN.
速率匹配方面,先要对母码进行子块交织,目的是降低译码复杂度和时延[45].然后采用重复、缩短和凿孔相结合的方式进行保留比特的选择.最后,为了提升高阶调制下的性能,在上行信道进行比特交织.协议中采用的三角形矩阵交织可以达到随机交织的性能[46].
编码结构方面,3种典型结构都被采纳.对于下行信道,采用分布式CRC-Polar的结构进行编码.这对下行信道独有的盲检测是非常有利的.协议中给出了信息比特序列的交织图样.对于上行信道,采用PC-CA-Polar和CA-Polar相结合的编码方案.如果K≥20,采用CA-Polar的编码结构;如果12≤K≤19,采用PC-CA-Polar的编码结构(低码率时性能略优于CA-Polar),奇偶校验比特数为3,构造规则如3.3所示.
5 性能分析本节首先在AWGN信道下对CA-Polar、分布式CRC-Polar码(D-CA-Polar)和PC-CA-Polar的性能和复杂度进行评估,然后给出分布式CRC-Polar码的提前终止性能.最后,按照TS 38.212协议构造5G-Polar码,与LTE-TBCC和5G-LDPC码进行性能对比.
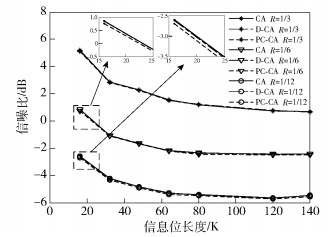
图 4给出了不同信息位长和码率的3种Polar码误块率(BLER,block error rate)达到10-3需要的信噪比.可靠性序列和速率匹配参照TS 38.212协议,码字结构按照第3节进行构造,采用19比特的CRC校验,L=32.可以看出,对于极短码(11 < K < 20)的情况,在码率为1/6和1/12时PC-CA-Polar比CA-Polar和分布式CRC-Polar好0.1~0.2 dB,而在其他信息比特长度和码率条件下3种Polar码的性能非常接近.因此,TS 38.212在上行信道中对K < 20和K≥20的控制信息分别采用PC-CA-Polar和CA-Polar的编码结构.
|
图 4 BLER为10-3时不同方案所需的信噪比 |
从译码方法来看,3种Polar码的区别在于校验比特的检测.统计了在BLER为10-3时K=48,R=1/3,L=8的3种Polar码进行一次完整SCL译码所需的查表、比较和加法运算,以PC-CA-Polar的复杂度为基准给出了复杂度的百分比, 如表 1所示.显然,计算复杂度由低到高依次为CA-Polar、分布式CRC-Polar、PC-CA-Polar.
|
|
表 1 计算复杂度统计 |
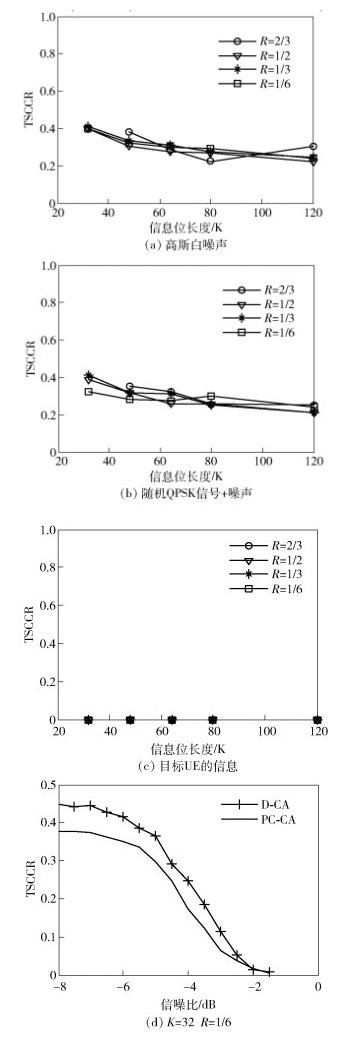
提前终止性能可以用提前终止率(ET Ratio,early termination ratio)和计算复杂度节约率(TSCCR,total saved computational complexity ratio)来衡量[43]. 图 5给出了分布式CRC-Polar码的计算复杂度节约率. 图 5(a)~(c)的性能是在目标UE误块率BLER为10-3的条件(对应的信噪比)下得到的.输入译码器的信息分别是:高斯白噪声,随机QPSK信号+高斯白噪声,目标UE的信息.可以看出,如果译码器输入是目标UE的信息,仅在信噪比很低的范围内获得40%的计算复杂度节约,此时BLER为100%,如图 5(d)“+”线.如果终端正确译码概率很高,提前终止没有显著的效果,如图 5(c).但如果译码器的输入不是目标UE的信息,如图 5(a)和(b),将会提前终止译码,从而节约20%~40%的计算复杂度.另外,图 5(d)也给出了华为公司在文献[44]中构造的具有提前终止性能的PC-CA-Polar的计算复杂度节约率.可以看出,分布式CRC-Polar能比PC-CA-Polar更大程度的节约计算复杂度.因此,综合考虑误码性能和复杂度问题,下行信道选择了分布式CRC-Polar的结构.
|
图 5 分布式CRC-Polar码的计算复杂度节约率 |
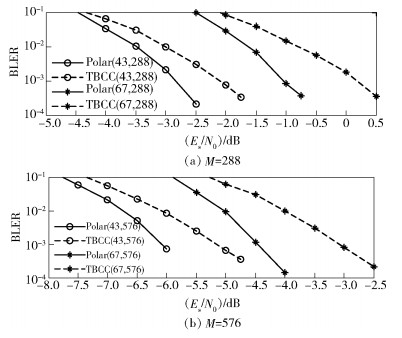
TBCC是LTE控制信道的主要编码方案,图 6在高斯信道下比较了码长为288和576的5G-Polar码(CRC-11,List-32)和LTE-TBCC的误块率,调制方式是QPSK.可以看出,5G-Polar码的性能明显优于LTE-TBCC,BLER为10-3时的增益如表 2所示.
|
图 6 高斯信道下5G-Polar码与LTE-TBCC性能 |
|
|
表 2 5G-Polar vs LTE-TBCC增益 |
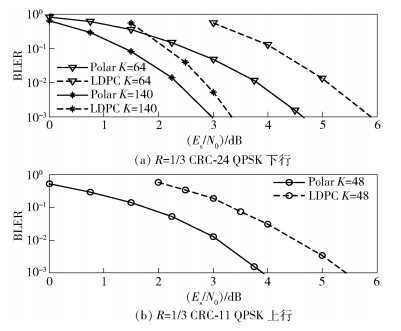
图 7和图 8分别给出了高斯信道和瑞利信道下5G-Polar码和5G-LDPC码的性能对比. Polar码和LDPC码都采用TS 38.212协议中的构造方法,码率为1/3.为了比较的公平性,LDPC码在上/下行信道分别采用11和24个比特的CRC校验.可以看出在短码情况下,5G-Polar码(List-8)的性能优于5G-LDPC码,BLER为10-3时的增益如表 3所示.

|
图 7 高斯信道下5G-Polar码与5G-LDPC码性能 |
|
图 8 瑞利信道下 5G鄄Polar 码与 5G-LDPC 码性能 |
|
|
表 3 5G-Polar vs 5G-LDPC增益 |
结合3GPP提案和TS 38.212协议介绍了5G-Polar码的3种结构类型,详细分析了每种码字构造的基本原理、关键特征和译码算法及其适用的条件.仿真比较表明,在极短码条件下PC-CA-Polar的性能略优于CA-Polar和分布式CRC-Polar,而在其他情况下3种结构的Polar有非常接近的误块率性能.在译码计算复杂度方面,CA-Polar的复杂度最低,而PC-CA-Polar的复杂度最高.因此,上行控制信道采用PC-CA-Polar(K < 20)和CA-Polar码(K≥20)混合的编码模式以增强性能.对于有盲检测需要的下行信道,分布式CRC-Polar码的提前终止译码技术能够有效的降低译码的计算复杂度和时延,因此分布式CRC-Polar码被用于下行控制信道.同时,通过仿真定量的给出了短码情况下5G-Polar码相对于LTE-TBCC和5G-LDPC码的性能增益.对于Polar码的未来研究工作,分布式CRC的交织设计,速率匹配算法以及与高阶调制和非正交多址的联合优化等方面依然是开放性问题,需要进一步深入探索.
| [1] | Plotkin M. Binary codes with specified minimum distance[J]. IRE Transactions on Information Theory, 1960, 6: 445–450. doi: 10.1109/TIT.1960.1057584 |
| [2] | Arikan E. Channel polarization:a method for constructing capacity achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051–3073. doi: 10.1109/TIT.2009.2021379 |
| [3] | Arikan E. A survey of reed-muller codes from polar coding perspective[C]//2010 IEEE Information Theory Workshop on Information Theory (ITW 2010). Cairo: IEEE Press, 2010: 1-5. |
| [4] | Korada S B, Sasoglu E, Urbanke R. Polar codes:characterization of exponent, bounds, and constructions[J]. IEEE Transactions on Information Theory, 2010, 56(12): 6253–6264. doi: 10.1109/TIT.2010.2080990 |
| [5] | Tal Ido, Vardy A. List decoding of polar codes[C]//2011 IEEE International Symposium on Information Theory (ISIT 2011). St Petersburg: IEEE Press, 2011: 1-5. |
| [6] | Chen Kai, Niu Kai. List successive cancellation decoding of polar codes[J]. Electronics Letters, 2012, 48(9): 501–502. doi: 10.1049/el.2012.0010 |
| [7] | Tal Ido, Vardy A. List decoding of polar codes[EB/OL]. (2012-05-31). https://arxiv.org/abs/1206.0050. |
| [8] | Tal Ido, Vardy A. List decoding of polar codes[J]. IEEE Transactions on Information Theory, 2015, 66(5): 2213–2226. |
| [9] | Li Bin, Shen Hui, David Tse. An adaptive successive cancellation list decoder for polar codes with cyclic redundancy check[J]. IEEE Communication Letters, 16(12), 2012: 2044–2047. |
| [10] | Samsung. CA-polar codes for small block length (R1-1708048)[EB/OL]. (2017-05-06). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [11] | 3rd Generation Partnership Project, Technical specification group radio access network. 3GPP TS 38.212 V15.0.0-2017, Multiplexing and channel coding (Release 15)[S]. Valbonne: 3GPP, 2017: 8-29. |
| [12] | Mori R, Tanaka T. Performance and construction of polar codes on symmetric binary-input memoryless channels[C]//2009 IEEE International Symposium on Information Theory (ISIT 2009). Seoul: IEEE Press, 2009: 1496-1500. |
| [13] | Mori R, Tanaka T. Performance of polar codes with the construction using density evolution[J]. IEEE Communications Letters, 2009, 13(7): 519–521. doi: 10.1109/LCOMM.2009.090428 |
| [14] | Tal Ido, Vardy A. How to construct polar codes[J]. IEEE Transactions on Information Theory, 2013, 59(10): 6562–6582. doi: 10.1109/TIT.2013.2272694 |
| [15] | Trifonov P. Efficient design and decoding of polar codes[J]. IEEE Transactions on Communications, 2012, 60(11): 3221–3227. doi: 10.1109/TCOMM.2012.081512.110872 |
| [16] | Wu Daolong, Li Ying, Sun Yue. Construction and block error rate analysis of polar codes over AWGN channel based on Gaussian approximation[J]. IEEE Communications Letters, 2014, 18(7): 1099–1102. doi: 10.1109/LCOMM.2014.2325811 |
| [17] | Huawei, Hisilicon. Polar codes-encoding and decoding (R1-164039)[EB/OL]. (2016-05-14). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_85/Docs/. |
| [18] | Huawei, HiSilicon. Details of the polar code design (R1-1611254)[EB/OL]. (2016-11-03). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_87/Docs/. |
| [19] | Huawei, HiSilicon. Sequence design for polar codes (R1-1706966)[EB/OL]. (2017-05-07). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [20] | Qualcomm Incorporated. FRANK polar construction: nested extension design of polar codes based on mutual information (R1-1705633)[EB/OL]. (2017-03-25). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_88b/Docs/. |
| [21] | Blasco-Serrano R, Thobaben R, Andersson M, et al. Polar codes for cooperative relaying[J]. IEEE Transactions on Communications, 2012, 60(11): 3263–3273. doi: 10.1109/TCOMM.2012.081412.110266 |
| [22] | NTT DOCOMO. Sequence design of polar codes (R1-1708489)[EB/OL]. (2017-05-06). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [23] | Samsung. Design of a nested sequence for polar codes (R1-1705425)[EB/OL]. (2017-03-25). http://www.3gpp.org/ftp/tsg_ran/WG1-RL1/TSGR1-88b/Docs/. |
| [24] | Wang Runxin, Liu Rongke. A novel puncturing scheme for polar codes[J]. IEEE Communications Letters, 2014, 18(12): 2081–2084. doi: 10.1109/LCOMM.2014.2364845 |
| [25] | Zhang Liang, Zhang Zhaoyang, Wang Xianbin, et al. On the puncturing patterns for punctured polar codes[C]//2014 IEEE International Symposium on Information Theory (ISIT 2014). Honolulu: IEEE Press, 2014: 121-125. |
| [26] | Ericsson. Puncturing and repetition of polar codes (R1-1707077)[EB/OL]. (2017-05-07). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [27] | MediaTek. Examination of NR coding candidate for low-rate applications (R1-167533)[EB/OL]. (2016-08-12). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_86/Docs/. |
| [28] | Huawei, HiSilicon. Polar code design and rate matching (R1-167209)[EB/OL]. (2016-08-13). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_86/Docs/. |
| [29] | Qualcomm Incorporated. Design of polar codes for control channel (R1-1700832)[EB/OL]. (2017-01-10). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_AH/NR_AH_1701/Docs/. |
| [30] | Nokia, Alcatel-Lucent Shanghai Bell. Polar codes design for UL control (R1-1701033)[EB/OL]. (2017-01-09). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_AH/NR_AH_1701/Docs/. |
| [31] | Nokia, Alcatel-Lucent Shanghai Bell. Details of CRC distribution of polar design (R1-1703497)[EB/OL]. (2017-02-15). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_88/Docs/. |
| [32] | Ericsson. Design of CRC-assisted polar code (R1-1701630)[EB/OL]. (2017-02-07). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_88/Docs/. |
| [33] | Qualcomm Incorporated. Early termination for polar codes (R1-1708644)[EB/OL]. (2017-05-06). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [34] | Ericsson. Polar code construction (R1-1707071)[EB/OL]. (2017-05-06). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [35] | ZTE. Performance evaluations on polar codes with distributed CRC bits (R1-1707181)[EB/OL]. (2017-05-06). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [36] | Huawei, HiSilicon. Distributed CRC for polar code construction (R1-1712167)[EB/OL]. (2017-08-16). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_90/Docs/. |
| [37] | Qualcomm Incorporated. Consideration of early termination for UCI (R1-1713466)[EB/OL]. (2017-08-17). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_90/Docs/. |
| [38] | ZTE. Performance evaluation of polar codes with distributed CRC bits (R1-1714629)[EB/OL]. (2017-08-26). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_90/Docs/. |
| [39] | Wang Tao, Qu Daiming, Jiang Tao. Parity check concatenated polar codes[J]. IEEE Communications Letters, 2016, 20(12): 2342–2345. doi: 10.1109/LCOMM.2016.2607169 |
| [40] | NTT DOCOMO. Distributed simple parity check polar codes (R1-1705757)[EB/OL]. (2017-03-25). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_88b/Docs/. |
| [41] | Huawei, HiSilicon. Polar code design (R1-1706965)[EB/OL]. (2017-05-07). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_89/Docs/. |
| [42] | Huawei, HiSilicon. Summary of polar code design for control channels (R1-1700088)[EB/OL]. (2017-01-10). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_AH/NR_AH_1701/Docs/. |
| [43] | Huawei, HiSilicon. Polar coding design for control channel (R1-1706193)[EB/OL]. (2017-04-09). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_88b/Docs/. |
| [44] | Huawei, HiSilicon. Parity check bits for Polar code (R1-1709996)[EB/OL]. (2017-06-20). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_AH/NR_AH_1706/Docs/. |
| [45] | Samsung. Rate matching scheme for polar codes (R1-1714179)[EB/OL]. (2017-08-17). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_90/Docs/. |
| [46] | Qualcomm Incorporated. Design and evaluation of interleaver for Polar codes (R1-1713474)[EB/OL]. (2017-08-17). http://www.3gpp.org/ftp/tsg_ran/WG1_RL1/TSGR1_90/Docs/. |


