2. 北京市卫星导航中心, 北京 100094;
3. 中国人民解放军31001部队, 北京 100092
为解决导航电文信息速率制约导航系统性能的问题,提出了一种基于码移键控调制和多进制低密度奇偶校验码的新型全球卫星导航系统(GNSS)信号编码调制技术.在-130 dBm的接收电平、误码率不大于10-7的指标下,该技术可以达到1 500 bit/s的有效信息速率,并且具有信号结构简单、与现有GNSS信号兼容性强等优势.理论分析和仿真结果证明,该技术突破了现有卫星导航信号体制下的信息速率极限,能够克服复杂信号结构造成的难以独立捕获跟踪的问题,在卫星导航系统中有比较重要的实用价值.
2. Beijing Satellite Navigation Center, Beijing 100094, China;
3. The 31001 forces of PLA, Beijing 100092, China
To solve the problem of navigation message rate limiting the performance of global navigation satellite system (GNSS), a new technology of GNSS signal design based on code shift keying modulation and non-binary low density parity check code is discussed. At a receiving level of -130 dBm and an error rate of no more than 10-7, the information rate can be up to 1 500 bit/s. Meanwhile, it has the advantages of simple signal structure and strong compatibility with existing GNSS signals. Theoretical analysis and simulation prove that this technology can break through the limit of information rate under the existing GNSS signal system, and overcome the difficulties of acquisition and tracking caused by complex signal structure. Therefore, it has important practical value in GNSS.
全球卫星导航系统(GNSS, global navigation satellite system)作为提供时空基准服务的重要基础设施,在军事、民用、科学等各个方面有着重要的作用.未来GNSS要实现更高的定位精度,除了对信号扩频调制方式进行优化设计以外,还需要实时传输精确星历、差分信息等内容,电文数据量与传统GNSS相比将大幅增加.例如,在北斗三号全球系统的设计中,用于承担全球定位报告业务的中地球轨道卫星的B2b信号,信息速率需大于500 bit/s,且误码率应低于10-6.电文的信息速率将直接影响北斗系统的服务质量,信息速率越高,则单条电文播发时间越短,播发频度越快,时效性越好.这对下一代GNSS的信号设计提出了更高的要求[1].
1 相关研究现状在目前GNSS广泛使用的基于二进制相移键控(BPSK, binary phase shift keying)和直接扩频序列调制(DSSS, direct sequence spread spectrum)的信号体制下,提高信息速率的方法有3种.
1) 提高扩频码速率.以民用GPS导航信号中的L1 C/A码信号为例.其采用码长为1 023的Gold码,扩频码速率为1.023 MHz,信息速率为50 bit/s[2],如果将码速率提高至10.23 MHz,码长和每比特周期中码重复的周期数不变,则信息速率可达到500 bit/s.但这种方法会同时增加频谱宽度,而且过快的扩频码速率也会显著增加接收机的处理复杂度.
2) 减小扩频码码长.将码长减小为原来的1/n,保持码速率和每比特周期中码重复的周期数不变,则信息速率可提高至原信息速率的n倍.由于码长长度有限,这种方法的提升空间不大,并且会导致扩频码的独立性和正交性变差,影响信号性能[3].
3) 减少扩频调制中每比特周期中扩频码重复的周期数.仍以C/A码为例,该方法可以将信息速率最高提高至1 000 bit/s,但扩频增益的损失会使解调门限升高13 dB.在-130 dBm的接收电平下,信号的误码率高达1.63×10-4,解调的可靠性将受到很大影响.
由上述分析可知,传统的提高导航信号信息速率的方法各有优缺点,而现代化的GNSS通过改变信号结构,能够实现信息速率的大幅提升.例如,准天顶卫星系统LEX实验信号的符号速率达到了2 000 symbol/s[3],除去信道编码之外的有效电文播发速率为1 744 bit/s.但LEX信号结构十分复杂,难以直接进行跟踪锁定,仅能依赖同一卫星上其他信号分量提供的码相位和多普勒频移辅助解调.因此,为实现下一代北斗系统高速、可靠地传播信息,需要一种全新的设计思路.
为应对北斗三号全球系统建设中高速数据传输所面临的挑战,笔者提出了一种基于码移键控(CSK, code shift keying)调制和多进制低密度奇偶校验码(NLDPC, non-binary low density parity check code)编码的GNSS电文多进制编码调制技术.一方面,利用CSK代替目前广泛使用的BPSK,可有效提高信息速率;另一方面,首次提出将NLDPC与CSK结合,以达到控制差错、降低误码率的目的,最大限度地发挥CSK调制的优势.
2 多进制编码调制技术传统GNSS信号使用的二进制扩频调制方式中,若干个扩频周期的波形仅传播1 bit信息,频带利用率不高.改用多进制调制,可以在不改变扩频码参数的情况下有效提高信息速率.为了实现较低的误码率,新信号需要同时使用高效的纠错码.
2.1 多进制扩频调制目前,常用的多进制扩频调制的方式有信息—BPSK/扩频码序列-正交相移键控(QPSK, quadrature phase shift keying)调制方法、平衡QPSK直接序列扩频、双通道QPSK直接序列扩频、最小频移键控直接序列扩频等[4],这些方法会改变信号的频率特性,并且需要重新对信号源和扩频码发生器进行设计,调制过程复杂,不利于星上实现.
CSK调制是一种新型的多进制调制方式,它具有信息速率快、灵活性高的优势,无需改变现有的扩频码结构,调制过程简单,适合在GNSS信号中使用[3, 5].在扩频码较长、电文数据量大的情况下,CSK调制具有和传统BPSK调制类似的频率特性,仅需在现有接收机的基础上对解扩模块进行改进即可实现.
CSK调制本质上是一种多进制正交信号,它的原理是:由一个基本扩频序列进行循环移位来表示不同的符号,在基本扩频码的基础上,每一位均向后循环位移n个位置,即可得到一段新的扩频码,这段码即可用来表示符号n[3]. CSK调制由2个参数决定:每个符号包括的比特数U及每个符号周期内扩频码的重复数N,表示为CSK(U, N).
通用的循环移位扩频码的数学表达式为
| $ {c_x}\left( t \right) = {c_d}\left( {\bmod \left[ {t - {m_x}{T_c},C{T_c}} \right]} \right) $ | (1) |
| $ \begin{array}{*{20}{c}} {{c_x}\left[ m \right] = {c_x}\left( {\bmod \left[ {m - {m_x},C} \right]} \right),}\\ {x = 0,1, \cdots ,M - 1} \end{array} $ | (2) |
| $ {c_x}\left( t \right) = \sum\limits_{m = 0}^{C - 1} {{C_x}\left[ m \right]{\rm{rect}}\left( {\frac{{t - m{T_c}}}{{{T_c}}}} \right)} $ | (3) |
其中:cd为基本扩频码,C为cd每个周期跨越的码片数,cx(t)为通过循环位移产生的一系列调制码,Tc为码片间距,mx为第x个符号的码与基本扩频码相比的移位数.
例如,使用一段长为1 023的码做CSK(4, 1)调制,可表示2 bit信息,4种符号所对应的移位码如图 1所示.
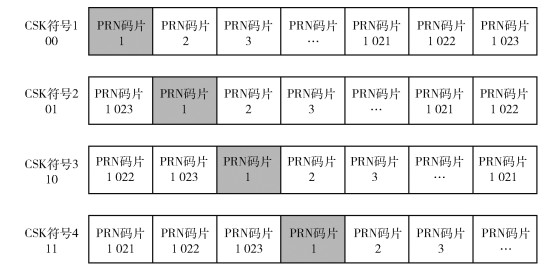
|
图 1 CSK符号示例 |
图 2为使用长度为4的扩频码对一段随机电文进行BPSK调制和CSK调制的原理示意图.在相同条件下,播发完相同长度的电文,CSK所需的时间是BPSK的一半,即CSK(4, 1)调制的信息速率是BPSK调制的2倍.
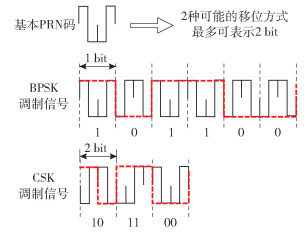
|
图 2 CSK(4, 1)的原理示意图 |
使用长度为1 023的C/A码,分别对一段信号进行BPSK调制和CSK(4, 1)调制,并对信号做快速傅里叶变换(FFT, fast Fourier transform),结果如图 3所示.

|
图 3 CSK调制和BPSK调制的频谱对比 |
由图 3可以看出,CSK(4, 1)的频谱特性和BPSK一致,但中频处的功率比BPSK信号低,即同等条件下,CSK(4, 1)的扩频增益将比BPSK低.
对于一个CSK信号,其扩频增益是伪码速率与信息码速率的函数[4],可表示为
| $ {G_p} = \frac{{{R_C}}}{{{R_b}}} $ | (4) |
其中:RC为伪随机码速率,Rb为信息码速率.选择GPS L1 C/A信号的标准C/A码,码长为1 023,周期为1 ms,码速率为1.023 MHz,则CSK(U, N)的扩频增益为
| $ {G_p} = \frac{{{R_C}}}{{{R_b}}} = 10\lg \frac{U}{{N/1\;023}} $ | (5) |
因此,使用CSK(U, N)可以将信息速率提高U/N倍,但同时会损失相应的扩频增益.通过使用合适的信道编码,能够在一定程度上弥补扩频增益的损失,保证信号的可用性.
2.2 NLDPC低密度奇偶校验码(LDPC, low density parity check code)编码是目前在信道领域发现的性能最好的信道编码之一,具有接近香农限的性能,已广泛应用到各类通信系统中[6]. LDPC具有译码复杂度低、可并行译码以及译码错误可检测等特点,且抗突发错误的能力强,非常适合在GNSS中使用.已有文献表明,NLDPC具有比二进制LDPC更好的性能,且与多进制正交调制的匹配型极佳,适合与CSK调制同时使用.
一个码长为N、信息位个数为k的LDPC记为LDPC(k, N),它可以由一个生成矩阵G来定义,信息序列s通过G编码映射成发送序列,则码字c=sG;也可以由一个一致校验矩阵H来等效描述,所有码字均满足cHT=0[6].校验矩阵的每一行表示一个校验约束,其中所有非零元素对应的码元变量构成一个校验集,用一个校验方程表示;校验矩阵的每一列表示一个码元变量参与的校验约束,当列元素不为零时,表示该码元变量参与了该行的校验约束. NLDPC可以看成二进制LDPC在有限域GF(q)(q=2p)上的推广,与二进制LDPC的区别在于,HM×N中的非零元素不是仅为1,而是取自GF(q)中的元素.
已有研究证明,NLDPC的性能优于二进制LDPC和LEX中使用的RS码[7].另外,GF(2p)上的NLDPC编码与对应的CSK(p, N)结合,可以在整个编码调制过程中将信息中的p个比特当作一个符号单元来处理,可有效避免信息-比特转换引入的信息量损失,能够最大限度地发挥CSK调制的优势.
3 基于NLDPC/CSK的编码调制基于CSK调制和NLDPC编码,一种新型的GNSS信号编码调制结构如图 4所示.电文采用类似于CNAV电文的数据块格式,每帧长度固定为2N个符号,其中前N个符号为信息主体,后N个符号为LDPC校验位.选用CSK调制,将每U bit的电文符号调制在一段扩频码上,形成扩频调制后的播发序列.
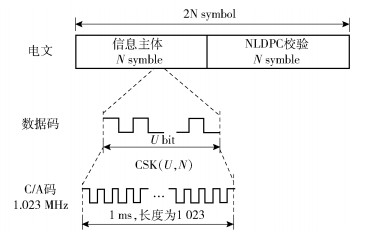
|
图 4 基于CSK调制和NLDPC的导航信号编码调制结构 |
由于CSK调制难以直接用于捕获跟踪,新信号需使用导频分量,导频分量与数据分量的功率比为1:1,调制在相互正交的载波上.导频分量上不调制电文,只包含测距码信息,因此,扩频码均为基本波形.其他参数与数据码一致.以使用CSK(4, 1)为例,新信号的生成仅需将现有生成模块的DSSS调制器更换为CSK调制器即可,比较容易实现,如图 5所示.

|
图 5 多进制编码调制信号生成原理 |
数据码的比特率Rb=1 000×
1) 根据式(5),对于同样的N,U每增加1,扩频增益将下降3 dB.而GF(2U+1)上的LDPC与GF(2U)相比,所带来的增益并不总能达到3 dB.因此,随着U的增大,信号的误码率将会提高.
2) NLDPC的编解码复杂度会随着U的增加大幅增加. NLDPC目前的解码算法均为循环解码,当U很大时,为了保证接收机解码的实时性,必须减少最大迭代次数,导致解码失败的可能性提高.
因此,信号设计的关键在于结合NLDPC的特性,合理选择U和N,平衡信息速率、误码率和复杂度,使信号具有最优的性能.
4 信号解调方法接收机使用导频分量实现信号的跟踪与捕获,然后将解算出的码相位用于数据分量的解调输入,对齐后进行解调和解码.
数据分量的处理上,与传统GNSS信号相比,需要增加NLDPC的译码步骤.目前使用较多的NLDPC译码算法是基于GF(q)的反向传播(BP, back propagation)算法和对数域置信传播(LLR-BP, log-likelihood ratio belief propagation)算法[8].下面以BP算法为例,进行简要介绍[7-8].
设输入码字为X,接收码字为Y,校验矩阵为H,多元LDPC的码域与调制的阶数相同.定义以下符号:
N(m):={n:hmn≠0}:参加第m个校验方程的变量节点的集合;
M(n):={m:hmn≠0}:第n个变量节点参加的校验方程的集合;
Pmna:在矩阵H的第m行的第n个非零元为a的条件下,第m个校验方程成立的概率;
Qmna:非零元在满足除第m个校验方程的其他所有校验方程的条件下,其值为a的后验概率.
循环译码的步骤如下.
1) 初始化
解调器接收符号的q个似然概率密度为
| $ P\left( {{\mathit{\boldsymbol{Y}}_n}\left| {{\mathit{\boldsymbol{X}}_a}} \right.} \right) = {\left( {\frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} \sigma }}} \right)^2}\exp \left[ { - \frac{{d_{{\mathit{\boldsymbol{Y}}_n},{\mathit{\boldsymbol{X}}_a}}^2}}{{2{\sigma ^2}}}} \right] $ | (6) |
其中:a=0, 1, …, q-1,Xa为多进制CSK的第a种循环码字,Yn为解调器接收到的第n个符号,d为欧氏距离.记各码元符号的q个初始后验概率为gna,则
| $ \begin{array}{*{20}{c}} {g_n^a = P\left( {{\mathit{\boldsymbol{X}}_a}\left| {{\mathit{\boldsymbol{Y}}_n}} \right.} \right) = \frac{{P\left( {{\mathit{\boldsymbol{Y}}_n}\left| {{\mathit{\boldsymbol{X}}_a}} \right.} \right)}}{{\sum\limits_{i = 0}^{q - 1} {P\left( {{\mathit{\boldsymbol{Y}}_n}\left| {{\mathit{\boldsymbol{X}}_a}} \right.} \right)} }} = }\\ {\frac{{\exp \left[ { - \frac{{d_{{\mathit{\boldsymbol{Y}}_n},{\mathit{\boldsymbol{X}}_a}}^2}}{{2{\sigma ^2}}}} \right]}}{{\sum\limits_{i = 0}^{q - 1} {\exp \left[ { - \frac{{d_{{\mathit{\boldsymbol{Y}}_n},{\mathit{\boldsymbol{X}}_a}}^2}}{{2{\sigma ^2}}}} \right]} }}} \end{array} $ | (7) |
2) 更新Pmna
| $ \begin{array}{*{20}{c}} {P_{mn}^a = \sum\limits_{\mathit{\boldsymbol{X}}:{x_n} = a} {\delta \left( {\sum\limits_{n' \in N\left( m \right)} {{\mathit{\boldsymbol{H}}_{mn'}}{\mathit{\boldsymbol{x}}_{n'}} = {\mathit{\boldsymbol{z}}_m}} } \right)} \times }\\ {\prod\limits_{j \in N\left( m \right)\backslash n} {Q_{mj}^{{x_j}}} } \end{array} $ | (8) |
3) 更新Qmna
| $ Q_{mn}^a = {a_{mn}}g_n^a\prod\limits_{j \in M\left( n \right)\backslash m} {P_{jn}^a} $ | (9) |
其中:amn为归一化因子,使得
4) 判决
每次迭代后,计算q个码元符号的伪后验概率:
| $ \bar Q_n^a = g_n^a\prod\limits_{j \in M\left( n \right)} {P_{jn}^a} $ | (10) |
选取最大值对应的Xa作为该符号的判决输出
综上,新信号生成和解调的完整流程如图 6所示.
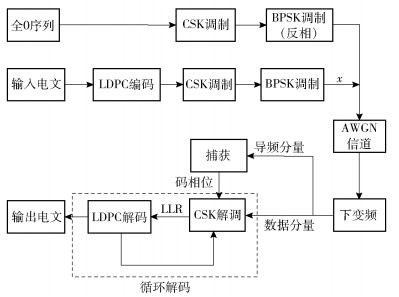
|
图 6 信号生成和解调流程 |
多进制编码调制信号的伪距和多普勒频移主要依赖导频信号提供,由于导频信号不调制任何电文信息,其解算方法和性能与传统GNSS信号一致.因此,重点讨论数据分量上的电文解调性能.
制约多进制编码调制信号参数选择的主要因素是NLDPC的解码复杂度.一个q进制的NLDPC编码,复杂度为O(q2)[8-9].假定其校验矩阵H的大小为M×N,行重为dc,列重为dv,以BP算法为例,每次迭代所需的运算量如表 1所示.
|
|
表 1 BP算法复杂度 |
参考相关研究成果[9-12],考虑到信号的实用性,选定16LDPC (1 152, 576)和64LDPC (1 200, 600)2种NLDPC给出信号实例并行比较,提出了4种方案.
方案1 16LDPC (1 152, 576)编码+ CSK(4, 1).每段电文长2 304 bit,每4 bit为一个符号,编码后长4 608 bit,即1 152 symbol.使用CSK(4, 1)调制,C/A码周期1 ms,每1个周期的C/A码表示1 symbol.
方案2 16LDPC (1 152, 576)编码+CSK(4, 2).每段电文长2 304 bit,每4 bit为一个符号,编码后长4 608 bit,即1 152 symbol.使用CSK(4, 2)调制,C/A码周期1 ms,每2个周期的C/A码表示1 symbol.
方案3 64LDPC (1 200, 600)编码+ CSK(6, 1).每段电文长3 600 bit,每6 bit为一个符号,编码后长7 200 bit,即1 200 symbol.使用CSK(6, 1)调制,C/A码周期1 ms,每1个周期的C/A码表示1 symbol.
方案4 4LDPC (1 200, 600)编码+ CSK(6, 2).每段电文长3 600 bit,每6 bit为一个符号,编码后长7 200 bit,即1 200 symbol.使用CSK(6, 2)调制,C/A码周期1 ms,每2个周期的C/A码表示1 symbol.
5.2 性能分析及对比使用BP算法解码,将64LDPC (1 200, 600)的最大迭代次数限制为40,2种码的译码性能与不使用任何信道编码时BPSK的误码率的对比结果如图 7所示.

|
图 7 NLDPC的误码率仿真曲线 |
由图 7可以看出,NLDPC编码能够十分有效地降低误码率,且进制数越高,效果越明显.由于最大循环次数的限制,64进制的LDPC随着信噪比的增加,误码率的降低速度相较16进制的LDPC略显缓慢.
在地面接收电平为-130 dBm,噪声电平为-111 dBm的情况下,从扩频增益、符号速率、有效电文比特率、误码率方面对5.1节中4种设计方案与LEX信号进行比较,结果如表 2所示.
|
|
表 2 多进制编码调制信号性能 |
4种多进制编码调制信号中,CSK(6, 1)+64LDPC虽然信息速率最快,但误码率很高,因而在实际情况中应用价值较低.其余3种均有较强的实用价值,可以根据系统不同的设计需求灵活选择.其中,速度最快的CSK(4, 1)+16LDPC比特率可达到2 000 bit/s,缺点在于误码率略高,适合用于传输数据量极大、重要性较低的电文信息,如精密单点定位信息、广域差分信息、全球等位报告等增值信息;CSK(4, 2)+16LDPC和CSK(6, 2)+64LDPC两种方案的误码率均低于10-7,符合北斗三号系统的误码率指标,可以直接用于新信号的设计.
与目前在使用的北斗系统D2导航电文、LEX实验信号以及现有文献中提及的新型信号相比,多进制编码调制信号都具有明显的优势.与D2信号相比,它突破了500 bit/s的信息速率限制,在误码率不高于10-6的条件下,信息速率1 000 bit/s的多进制编码调制电文,最低解调电平比D2低大约3 dBm.与LEX信号相比,它无需使用复杂的二级码结构,具有信号结构简单,可独立实现定位,与其他导航系统兼容性良好的特点.与Peña等[5]提出的只使用CSK调制的方法相比,NLDPC的使用有效降低了误码率,信息速率相同的情况下,所提出的方法的最低接收电平可以降低约15 dBm.
另外,值得注意的是,笔者选用的NLDPC均是码率R=1/2的标准编码,改用相同进制更高码率的编码,可在相同符号速率下获得更高的有效信息速率.由于所提出的方法均已超出500 bit/s的设计指标,所以未对此进行深入探讨.未来GNSS如对电文速率提出更高的要求,此处尚有较大的挖掘空间.
6 结束语针对传统模式下GNSS电文速率难以达到新一代北斗系统中B2b信号设计要求的问题,提出了一种GNSS电文多进制编码调制技术.该技术利用CSK调制可大幅提高信息速率,同时使用NLDPC降低了误码率.理论分析和仿真结果证明了该技术具有信号结构简单,信号速率极高,误码率低,与现有GNSS信号兼容性良好等特点.针对北斗三号系统实际需求,进一步给出了3种具体方案,在地面接收电平为-130 dBm,噪声电平为-111 dBm的情况下,比特率分别为1 000 bit/s、1 500 bit/s、2 000 bit/s.实际应用中,可根据电文数据量和接收机的最大运算能力等因素灵活选择.理论分析和仿真结果表明,该技术突破了传统GNSS信号的信息速率极限,解决了现有信号结构制约电文内容的问题,对未来GNSS信号设计具有重要的参考价值.
| [1] | Chen J P. Analysis of modernization GNSS navigation message's designing[J]. Journal of Electronics and Information Technology, 2011, 33(1): 211–217. doi: 10.3724/SP.J.1146.2010.00584 |
| [2] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. |
| [3] | Kogure S, Kishimoto M, Sawabe M, et al. Introduction of IS-QZSS (interface specification for quasi zenith satellite system)[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007). Fort Worth, TX: [s. n. ], 2007: 3008-3014. |
| [4] | 田日才, 迟永钢. 扩频通信[M]. 北京: 清华大学出版社, 2014. |
| [5] | Peña A J G, Paimblanc P, Salós D, et al. Investigation of CSK as a Candidate for Future GNSS Signals[J]. Ferroelectrics, 2013, 121(1): 335–342. |
| [6] | 史治平. 多元LDPC码及其在无线通信中的应用[M]. 北京: 国防工业出版社, 2012. |
| [7] | 陈俊斌.多进制LDPC码与RS码的性能比较研究[D].厦门: 厦门大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10384-2007054905.htm |
| [8] | 吴晓丽.多进制LDPC码的编译码算法及结构研究[D].西安: 西安电子科技大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10701-2010038892.htm |
| [9] | 张雅倩.多进制LDPC码编译码算法研究[D].哈尔滨: 哈尔滨工程大学, 2012. |
| [10] | Chen Weigang, Cao Yan, Xia Xiaoxiao, et al. Constructing nonbinary LDPC codes for satellite navigation system[J]. Computer Applications and Software, 2016, 33(4): 108–110. |
| [11] | 马振洲.多元LDPC编码与调制联合优化设计研究[D].成都: 电子科技大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10614-2009166038.htm |
| [12] | Mackay D J C, Neal R M. Near Shannon limit performance of low density parity check codes[J]. Electronics Letters, 1996, 32(6): 457–458. |


