2. 中钢集团马鞍山矿山研究院有限公司 金属矿山安全与健康国家重点实验室, 安徽 马鞍山 243000
为了保证无线传感器网络(WSN)在深井中能有效地工作,提出了一种改进蚁群的反向传播(BP)神经网络WSN数据融合算法(IFA-IACOBP).通过规划蚂蚁运动方向和引入节点剩余能量对蚁群算法启发因子进行改进,优化蚂蚁下一跳节点选择概率,利用改进后的蚁群算法对BP神经网络进行优化,引入井下WSN数据融合,数据经两级融合处理后,能去除大部分冗余信息.仿真实验结果表明,IFA-IACOBP算法能有效减少网络数据通信量,提高数据实时性,降低网络能耗,延长网络寿命.
2. State Key Laboratory of Safety and Health for Metal Mines, Sinosteel Maanshan Institute of Mining Research Company, Anhui Maanshan 243000, China
In order to ensure the effective working of wireless sensor network (WSN) in deep mine, an information fusion algorithm based on improved ant colony optimization back-propagation (BP) neural network in WSN (IFA-IACOBP) is proposed. The heuristic factor of ant colony optimization (ACO) is improved by planning the direction of ants' motion and introducing the residual energy of nodes to improve the selection probability of the ant next-hop node. The improved ant colony algorithm is used to optimize the BP neural network, which is applied to WSN information fusion in mine. These data are processed by two-level fusion, which can remove most redundant information. Simulation results show that the IFA-IACOBP algorithm can effectively decrease the network data communication, improve data real-time performance, reduce network energy consumption and prolong network lifetime.
无线传感器网络(WSN, wireless sensor networks)节点能量有限,且不能更换电源,如何合理高效利用能量,延长网络寿命成为其研究的核心问题之一[1-2].数据的采集、处理和转发都需要消耗能量,而转发数据是最耗能的[3]. WSN节点一般是较高密度覆盖在监测区域内,会产生大量冗余数据,传送这些冗余数据势必会消耗大部分能量[4].数据融合能对数据进行冗余处理,减少网络数据的传输量,降低节点能耗,延长网络寿命[5-6].
有学者将反向传播(BP, back propagation)神经网络模型引入WSN处理数据融合问题[7-8].然而BP神经网络对初值敏感,易陷入局部最优,在实际应用时会受到一定限制.李兆祥[9]采用遗传算法对BP神经网络结构、权值和阈值进行优化,提出了一种基于遗传BP神经网络的数据融合模型(GABP, data fusion model based on genetic algorithm and BP neural network),对延长网络寿命有一定效果;赵亚光[10]将蚁群算法引入神经网络的蚁群神经网络数据融合算法(ACOBP, data fusion algorithm based on ant colony algorithm and BP neural network),对BP神经网络的参数和结构进行了优化,网络寿命获得了一定的延长.王晨等[11]引入一种新的连续蚁群优化算法来确定网络权值,在一定程度上克服了传统BP算法训练神经网络带来的缺陷.张艳蕊[12]提出将改进蚁群算法与神经网络相结合,通过全局和局部更新信息素的更新机制优化神经网络权值和阈值,能有效减少数据通信量.
上述算法是针对一般场景提出的,而深矿井下环境复杂,对节点能量的损耗更加突出.为了减少节点能耗,保障数据可靠传输,提出一种基于改进蚁群的BP神经网络WSN数据融合算法(IFA-IACOBP, information fusion algorithm based on improved ant colony optimization BP neural network in WSN),对深矿井的现代智能监测具有现实意义.
1 改进蚁群算法 1.1 经典蚁群算法蚁群算法(ACO, ant colony optimization)是由蚂蚁觅食得到启发而来的[13],蚂蚁在没有事先被告知食物在哪里的境况下,找到食物的最短路径,还可以根据环境的改变搜索到新的路径.主要是由于蚂蚁在经过的路径上会释放出信息素,信息素主要包括路况信息和信息强度,指引着更多蚂蚁向信息素多的方向行进. ACO是一种通过信息素多少来寻找优化路径的机率型算法. t时刻时,蚂蚁(k=1, 2, …, n)在节点i处选择节点j的概率为
| $ P_{ij}^k = \left\{ \begin{array}{l} \frac{{\tau _{ij}^\alpha \eta _{ij}^\beta }}{{\sum\limits_{j \in {U_k}} {\tau _{i,s}^\alpha \eta _{i,s}^\beta } }},\;\;\;\;j \in {U_k}\\ 0,\;\;\;\;j \notin {U_k} \end{array} \right. $ | (1) |
其中:τij为节点i、j间的信息素,τi, s为节点i、sink间的信息素;ηij为启发因子,表示能见度因素,通常为ηij=1/dij,dij为节点i~j的距离. α表示信息启发因子,一般α=1~5范围内,β期望值启发因子,一般β=1~5范围内,α最佳取值在1左右,β在2~5之间为最优[14]. Uk表示蚂蚁k下一步可以选择的节点集合.
T时刻后,蚂蚁的一次循环结束,各路径信息素按式(2)进行调整:
| $ {\tau _{ij}}\left( {t + T} \right) = \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}} $ | (2) |
其中:Δτij表示此次循环路径(i, j)信息素增量;ρ为信息素衰减系数,取ρ < 1可防止路径上信息素的无限累积.
1.2 ACO改进上述ACO收敛速度慢,全局搜索能力差,直接运用至拥有大量传感器节点的WSN数据融合算法有一定局限性.此外,ACO并未将节点能量考虑入内,若是直接运用会导致簇首节点过早死亡.针对这些问题,尝试对ACO做一些改进.
张艳蕊[12]对最优路径的选择概率P提出了改进,如
| $ P = \left\{ \begin{array}{l} \arg \max \left\{ {\tau _{ij}^\alpha \eta _{ij}^\alpha } \right\},\;\;\;\;q \le {q_0}\\ P_{ij}^k,\;\;\;\;其他 \end{array} \right. $ | (3) |
其中:q0为寻优和探寻新路径的相对重要性,其取值范围为[0, 1];q为[0, 1]上的任意随机数.当q≤q0时,按照式(3)选择最优路径;否则按照式(1)随机选择路径.
启发因子是帮助蚂蚁在选择路径时,以更大的概率选择最短路径,两点间的距离越短,ηij越大,则蚂蚁选择该路径的概率越大.而ηij=1/dij仅考虑了节点与节点之间的距离关系,并没有考虑能量.
先对蚂蚁运动方向进行规划.在深井巷道中,节点采集到的数据需要传输至sink节点,而sink一般位于深井出口或进口位置,为了避免数据向后传,需要对蚂蚁运动的方向角进行规划,图 1所示为蚂蚁运动方向规划.
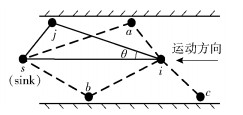
|
图 1 蚂蚁运动方向规划 |
节点往sink节点传输数据时,按照ACO,蚂蚁选择下一跳节点时,启发因子仅依赖于节点i与节点j的距离关系,可能会使得数据反向传输.虽然数据最终会传至sink节点,但数据反向传输后再传回来需要消耗大量能量,缩短网络寿命.因此只有当θ < ±90°时(θ为运动方向与下跳节点传输路径间夹角),蚂蚁才会朝着sink节点运动.此外,若节点i能量足够,可以单跳方式选择距sink节点更近的节点j传输数据,即节点i与下一跳节点构成的θ角度较小;否则就以多跳方式传输数据.
从节点能量入手,对节点能量影响因子ξ做出如下定义:
| $ \xi = \frac{{{E_j}}}{{{E_0}}} \times 100\% $ | (4) |
其中:E0表示节点初始能量,Ej为节点j当前剩余能量.节点剩余能量越多,ξ越大;随着时间推移,节点剩余能量会下降,随之ξ也变小.
考虑蚂蚁运动方向,对启发因子进行改进,如:
| $ {\eta _{ij}} = f\left\{ {\theta ,{d_{ij}}} \right\} $ | (5) |
角度θ越小、距离dij越短,启发因子ηij就越大.改进后的节点选择概率Pij, 改k、P改为
| $ P_{ij,改}^k = \left\{ \begin{array}{l} \frac{{\tau _{ij}^\alpha \eta _{ij}^\beta \xi _{ij}^\lambda }}{{\sum\limits_{j \in {U_k}} {\tau _{i,s}^\alpha \eta _{i,s}^\alpha \xi _{i,s}^\lambda } }},\;\;\;\;j \in {U_k}\\ 0,\;\;\;\;\;j \notin {U_k} \end{array} \right. $ | (6) |
| $ {P_{改}} = \left\{ \begin{array}{l} \arg \max \left\{ {\tau _{ij}^\alpha \eta _{ij}^\beta \xi _{ij}^\lambda } \right\},\;\;\;\;\;q \le {q_0}\\ P_{ij,改}^k,\;\;\;\;\;其他 \end{array} \right. $ | (7) |
其中:λ为能量启发因子,表示节点剩余能量对路径选取的影响程度. λ越大,蚂蚁越倾向于选择能量更充足的下一跳节点作为路径.
2 IFA-IACOBP算法 2.1 网络模型为了及时高效对传感器节点采集到的数据处理和传输,需要对这些数据进行去冗,减少数据的通信量,提高数据实时性. 图 2为IFA-IACOBP算法的两级神经网络结构示意图.第1级神经网络是由普通节点通过第1级隐层神经元功能函数对采集的原始数据进行预处理,预处理结果经输出层输出;第2级神经网络是由簇首节点对接收到的第1级预处理结果进行归一化,将归一化结果经第2级隐层神经元功能函数处理后通过输出层输出结果;将两级融合处理后的结果传输至sink节点,可以有效减少数据传输量.
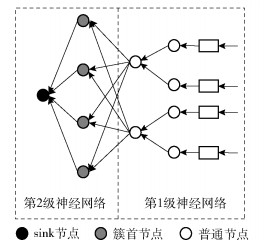
|
图 2 IFA-IACOBP算法两级神经网络结构 |
将上述改进后的ACO引入BP神经网络,实现步骤如下:
1) 传感器节点采集其周围数据;
2) 确定问题规模,对BP神经网络的输入、输出个数进行初始化;
3) 将改进后的ACO引入BP神经网络进行优化,并运用至井下监测.普通节点将采集到的原始数据经第1级神经网络结构进行融合处理,经簇首节点归一化后再输入至第2级神经网络结构处理,将两级融合处理结果传输至sink节点.
2.3 改进蚁群算法优化BP神经网络改进ACO优化BP神经网络算法的基本思想是构建优化目标函数,改进ACO的同时,优化BP神经网络的拓扑结构、权值和阈值.先用改进ACO对数据进行预处理,优化权值和个数,得到一个全局较优解,并将这些值作为BP神经网络的结构与初值,用样本训练来进行进一步局部的精确寻优.这样可以提高BP神经网络泛化能力、收敛能力和求解精度,简化训练,减少训练时间,克服传统神经网络拓扑结构和初始权值确定过程中的随意性所带来的网络振荡,也避免了网络易陷入局部解的缺陷.改进ACO优化BP神经网络算法流程如下:
第1步 初始化参数:蚂蚁数量n,信息启发因子α,期望值启发因子β,能量启发因子λ,信息素衰减系数ρ,令初始迭代次数N=0,设最大迭代次数为Nmax,并确定BP神经网络拓扑结构、初始权值和阈值.
第2步 计算P改:根据信息素τij、节点间距dij、角度θ和节点剩余能量Ej计算节点选择概率P改,并由P改确定蚂蚁个体运动方向.
第3步 迭代次数是否满足N=Nmax:①不满足,则继续迭代、更新信息素,并反至第2步;②满足,则得到最佳权值、阈值赋给BP神经网络进行更新.
第4步 结束条件σq < 阈值是否满足:①不满足,则重新调整误差σq(见式(9));②满足,则训练结束,输出结果.
2.4 IFA-IACOBP算法神经元模型IFA-IACOBP算法神经元模型分为两级,分别作用于普通节点和簇首节点,经两级融合处理后,将最终结果传输至sink节点.
第1级数据融合的神经网络是3层神经网络,包含输入层、隐含层和输出层.普通节点采集参数信息,经隐含层预处理后再输出.该层次的神经元功能函数与井下具体参数有关,以监测温度为例,对平均温度神经元的功能模型进行分析.设第1级神经元拥有n个输入和1个输出值,即平均温度Tave.采用加权平均的功能函数,则平均温度神经元的功能模型为
| $ {T_{{\rm{ave}}}} = \frac{1}{n}\sum\limits_{k = 1}^n {{\omega _{1,k}}{T_k}} $ | (8) |
其中:Tk为第k个节点采集的温度值,ω1, k为第1级神经网络权值,取ω1, k =1.
第2级神经网络模型也分为3层,数据融合发生在簇首节点.簇首节点对接收到的普通节点的预处理结果先进行归一化,将归一化结果经隐层神经元功能函数处理后通过输出层输出结果.
设归一化样本序列为y1,y2,…,ym,可以得到参数的平均值和标准值为
| $ \left. \begin{array}{l} {y_{{\rm{ave}}}} = \frac{1}{m}\sum\limits_{q = 1}^m {{y_q}} \\ {\sigma _q} = {\left( {\sum\limits_{q = 1}^m {{{\left( {{y_q} - {y_{{\rm{ave}}}}} \right)}^2}} } \right)^{\frac{1}{2}}} \end{array} \right\} $ | (9) |
其中:yave和σq分别表示q个参数的平均值和误差值,经簇首节点归一化后输出,输出值为
| $ {u_q} = \left( {{y_q} - {y_{{\rm{ave}}}}} \right){\sigma _q} $ | (10) |
uq经过第2级隐层神经元功能函数进行融合数据,则输出层神经元功能函数为
| $ Y = \sum\limits_{q = 1}^m {\left( {{\omega _{2q}}{u_q} + {v_q}} \right)} $ | (11) |
其中:ω2q为簇首节点的权值;vq表示簇首节点的修正值.
3 仿真结果与分析采用matlab对IFA-IACOBP算法的性能进行验证,从数据融合率、网络寿命、sink节点接收的数据包个数三方面进行分析,与GABP算法和ACOBP算法相比较,仿真参数设置如表 1所示.
|
|
表 1 仿真参数设置 |
1) 数据融合率
数据融合率在不同的文献中有不同的定义,此处定义数据融合率为
| $ {R_{\rm{f}}} = \frac{{{D_{\rm{o}}} - {D_{\rm{f}}}}}{{{D_{\rm{o}}}}} $ | (12) |
其中:Do表示原始数据,Df表示融合后输出的数据. Rf越大,即去冗余数据越多.
图 3给出了3种算法数据融合率Rf的对比情况,σq-1为数据精度.当σq-1=20时(σq=0.05)的Rf是IFA-IACOBP算法为0.42、ACOBP算法为0.25、GABP算法为0.16.在0 < σq-1≤20内,IFA-IACOBP、ACOBP、GABP算法的平均Rf分别为0.69、0.60、0.55.可见IFA-IACOBP算法在同等数据精度下,能融合较多的数据.随着σq-1的提高,IFA-IACOBP算法的Rf优势更明显,相较于另外2种算法始终具有较好的融合效果.

|
图 3 3种算法数据融合率Rf对比 |
2) 网络寿命
WSN由电池供电,具有有限能量,一旦出现单个或局部区域传感器能量无法供其正常工作(即一是节点能量耗尽既不能采集数据也不能传输数据;二是可以进行数据采集,去无法传输数据),均会导致监测出现盲区,监测盲区越多,网络采集数据越不可靠,发生危险的可能性越大.尤其在复杂环境的深井中,必须保证数据的可靠性,为此定义当网络节点存活率为80%时,传感器采集的数据为可靠数据,若低于80%则视为无效网络,需要补充新的传感器.
图 4给出了3种算法网络寿命(轮数)对比的情况,当网络存活节点数为80时,WSN监测属于有效网络,节点采集到的数据是可靠的.由图可知,此时采用GABP算法为917轮,ACOBP算法为1 210轮,IFA-IACOBP算法为1342轮(分别是GABP的1.46倍、ACOBP的1.11倍),IFA-IACOBP算法较其他两种算法明显延长了网络寿命.
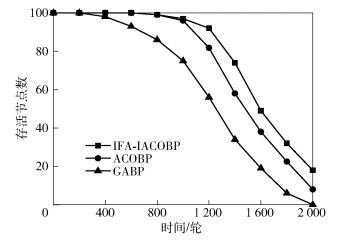
|
图 4 3种算法网络寿命对比 |
3) sink节点接收的数据包数量
图 5显示了3种算法对sink节点接收数据包的影响情况,3种算法都进行了数据融合处理,普通节点和簇首节点过滤大部分冗余数据,降低了数据传输量. IFA-IACOBP算法基本在任一时刻传输的数据量均最少,并且随着时间的增加,IFA-IACOBP算法优势越明显.对比其他2种算法,IFA-IACOBP算法能更为有效地进行数据融合,提高数据传输可靠性,有效延长了网络寿命.

|
图 5 3种算法网络寿命对比 |
针对深部矿井复杂环境,提出了一种基于改进蚁群的BP神经网络WSN数据融合算法(IFA-IACOBP).通过规划蚂蚁运动方向,引入节点剩余能量对经典蚁群算法的启发因子进行改进,从而改进蚂蚁下一跳节点选择概率.将改进后的蚁群算法用来优化BP神经网络并运用至深井监测WSN的信息融合.传感器节点采集到的源数据两级融合处理后,将少量代表源数据特征的信息传输至Sink节点.仿真实验结果表明,IFA-IACOBP算法有效减少了节点数据通信量,提高了数据传输实时性,降低了整个网络能耗,有效地延长网络生存周期.
| [1] |
王翥, 胡屏, 董梦梦, 等. 多贪婪准则条件下中继节点布局算法[J]. 北京邮电大学学报, 2016, 39(3): 91–94, 104.
Wang Zhu, Hu Pin, Dong Mengmeng. Relay node placement algorithm under the condition of multi greedy criterion[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(3): 91–94, 104. |
| [2] |
刘洲洲, 王福豹. 一种能耗均衡的无线传感器网络加权无标度拓扑研究[J]. 物理学报, 2014, 63(19): 59–66.
Liu Zhouzhou, Wang Fubao. Research on weighted scale-free topology with balancing energy consumption characteristics in wireless sensor networks[J]. Acta Physica Sinia, 2014, 63(19): 59–66. |
| [3] | Manshahia M S. Wireless sensor networks:a survey[J]. International Journal of Scientific & Engineering Research, 2016, 7(4): 710–716. |
| [4] |
杨靖, 熊伟丽, 秦宁宁, 等. 用于无线传感器网络的高能效数据收集算法[J]. 吉林大学学报, 2011, 41(6): 720–725.
Yang Jing, Xiong Weili, Qin Ningning, et al. Energy-efficient data gathering algorithm for wireless sensor networks[J]. Journal of Jilin University, 2011, 41(6): 720–725. |
| [5] |
邱雪松, 蔺艳斐, 邵苏杰, 等. 一种面向智能电网数据采集的传感器聚合布局构造算法[J]. 电子与信息学报, 2015, 37(10): 2411–2417.
Qiu Xuesong, Lin Yanfei, Shao Sujie, et al. Sensor aggregation distribution construction algorithm for smart grid data collection system[J]. Journal of Electronics & Information Technology, 2015, 37(10): 2411–2417. |
| [6] |
徐晓斌, 张光卫, 孙其博, 等. 一种误差可控传输均衡的WSN数据融合算法[J]. 电子学报, 2014, 42(6): 1205–1209.
Xu Xiaobin, Zhang Guangwei, Sun Qibo, et al. Precision configurable data aggregation algorithm in WSNs[J]. Acta Electronica Sinica, 2014, 42(6): 1205–1209. doi: 10.3969/j.issn.0372-2112.2014.06.025 |
| [7] | Sun Lingyi, Cai Wei, Huang Xianxiang. Data aggregation scheme using neural networks in wireless sensor networks[C]//International Conference on Future Computer and Communication. Wuhan: IEEE, 2010: 725-729. |
| [8] | Li Shi, Liu Mengyao, Xia Li. WSN data fusion approach based on improved BP algorithm and clustering protocol[C]//Control and Decision Conference. Qingdao: IEEE, 2015: 1450-1454. |
| [9] | 李兆祥.无线传感器网络数据融合的算法研究[D].武汉: 武汉理工大学, 2011. |
| [10] | 赵亚光.基于蚁群算法和BP神经网络的WSN数据融合算法研究[D].昆明: 云南大学, 2013. |
| [11] |
王晨, 陈增强. 基于连续蚁群算法融合的神经网络RFID信号分布模型[J]. 东南大学学报, 2013, 43(S1): 210–214.
Wang Chen, Chen Zengqiang. RFID signal distribution model based on neural network combined with continuous ant colony optimization[J]. Journal of Southeast University, 2013, 43(S1): 210–214. |
| [12] | 张艳蕊.基于改进蚁群算法的BP神经网络优化的研究与应用[D].沈阳: 东北大学, 2013. |
| [13] | Ye Zhengmao, Mohamadian H. Adaptive clustering based dynamic routing of wireless sensor networks via generalized ant colony optimization[J]. Ieri Procedia, 2014(10): 2–10. |
| [14] | 刘波.蚁群算法改进及应用研究[D].秦皇岛: 燕山大学, 2010. |


