在相关性快速过滤特征选择算法(FCBF)基础上,通过最大相关系数的方式改进FCBF算法.首先,通过最大相关系数和对称不确定性度量准则,计算出每个特征与标签之间的相关度量值,并按照数值大小顺序进行排序;其次,通过最大相关系数和近似马尔可夫毯原理进行无关特征和冗余特征的筛选,最终选择出最优特征子集.在加利福尼亚大学欧文分校的机器学习库(UCI)的8个公开数据集中进行对比实验结果表明基于最大相关系数的特征选择算法(NFCBF)总体优于FCBF算法,它所选择出特征数比FCBF算法所选择特征数平均少了3.625个,分类准确率平均提高了0.075%.与互信息最大算法(MIM)、最少的绝对收缩和选择算法(Lasso)和岭算法(Ridge)等相比也具有明显的优势.
Based on the correlation fast Filtering Feature selection algorithm (FCBF), which is improved by the maximum correlation coefficient. Firstly, It calculates the correlation measure between each feature and label with the 'maximum normalized information coefficient' criterion and 'measurement principle of symmetric uncertainty' and sort these feature according to the calculated value.Finally, It filters irrelevant features and redundant features by the 'maximum normalized information coefficient' criterion and approximate Markov Blanket and obtain the optimal feature subset. Experimental results on machine learning repository of university of california irvine(UCI) eight open datasets show that NFCBF algorithm outperforms FCBF algorithm. The number of features selected by feature selection algorithm based on maximum information coefficient (NFCBF algorithm) is less than 3.625 of the selected feature subset of FCBF algorithm, and the classification accuracy is improved by 0.075%. NFCBF algorithm gives better performance than mutual information maximization algorithm(MIM), Least absolute shrinkage and selection operator algorithm(Lasso) and Ridge algorithm.
随着大数据技术的深入发展,大量的数据从互联网领域、医学领域、工业制造领域等产出[1].而机器学习就是要深入到这些领域中,获取有价值的数据信息,并支持它们相关决策工作.然而,这些数据中存在着大量的无关性或者冗余性的数据,而无关或者冗余性的数据往往又会影响机器学习算法的性能[2].特征选择技术就是要寻找最优的特征子集,而该子集可以提高机器学习算法的性能.因此,特征选择技术为众多的机器学习算法带来大量好处,比如,可提高相关机器学习的执行速度和学习准确率[3],同时,可降低它们的存储空间和机器学习训练与测试的成本.特征选择技术[4-12]有如上的优点,得到飞速的发展.但是,常见的特征选择算法又常常忽略了特征之间的内在结构,导致一些无关特征或者冗余特征没有识别出来.为了解决上面的问题,笔者提出通过最大信息系数理论[4]去修正经典快速过滤的特征选择算法(NFCBF,feature selection algorithm based on maximum information coefficient).
1 相关工作近几十年来,信息理论已经广泛应用在过滤式特征选择算法领域[13]中,例如:互信息最大算法(MIM,mutual information maximization)[10],它通过计算每个特征和目标标签之间的互信息,并根据计算后的结果按照数值大小的顺序进行排序.最大相关最小冗余特征选择算法[5]采用前向贪婪搜索方式,对候选特征与目标标签之间以及候选特征与已选特征之间进行相关性和冗余性进行检测. FCBF算法[9]采用互信息的对称不确定度量作为特征关系的度量准侧. Brown[11]使用最大信息系数来检测特征之间的冗余,并且使用前向贪婪搜索算法进行特征子集的寻找,以此寻找较好的特征子集.
2 信息熵和最大信息系数 2.1 熵与互信息定义1 信息熵[13]解决了对信息随机变量不确定性的度量.设X为离散随机变量,那么X的熵为
| $ H\left( X \right) =-\sum\limits_{i = 1}^m {p\left( {{x_i}} \right)\log p\left( {{x_i}} \right)} $ | (1) |
定义2 条件熵表示为当随机变量Y单独发生时,随机变量X发生的条件概率分布.
| $ H\left( {X\left| Y \right.} \right) =-\sum\limits_{y \in Y} {p\left( y \right)\sum\limits_{x \in X} {P\left( {x\left| y \right.} \right)\log p\left( {x\left| y \right.} \right)} } $ | (2) |
定义3 互信息可以通过式(1)(2)用熵进行表示
| $ I\left( {X;Y} \right) = H\left( X \right)-H\left( {X\left| Y \right.} \right) = H\left( Y \right)-H\left( {Y\left| X \right.} \right) $ | (3) |
然后,再依据式(2) (3)进一步得
| $ 0 \leqslant I\left( {X;Y} \right) \leqslant \min \{ H\left( X \right), H\left( Y \right)\} $ | (4) |
Reshef等[8]提出的最大信息系数理论重点描述了变量间度量关系,通过这种度量关系进一步得到它们间的非函数依赖关系.通常最大信息系数可以通过互信息和熵进行计算.
从式(4)可知,I(X; Y)的上界是H(X)和H(Y)之间的最小值,它的下界是0.由于熵值变化非常大,不确定的熵值会导致I(X; Y)值也不合理.因此,有必要对I(X; Y)进行最大信息系数处理.因为最大信息系数化可以弥补多值特征中互信息的偏差,并将其取值范围限制在[0, 1]以内.因此,对于随机变量X和Y的最大信息系数,就可以由H(X)和H(Y)的最小值来决定,具体公式为
| $ {I_{{\text{max}}}}\left( {X;Y} \right) = \frac{{I\left( {X;Y} \right)}}{{\min \{ H\left( X \right), H\left( Y \right)\} }} $ | (5) |
通过上面的分析,特征X和标签Y之间的相关性可以通过最大相关信息系数Imax(X; Y)进行描述,而衡量特征之间的冗余特征,也可以通过Xi∈S,Xj∈S(i≠j)之间的最大相关信息系数Imax(Xi; Xj)进行描述.
3.1 相关性分析首先,定义每个特征Xi与Y最大信息系数Imax(X; Y);其次,计算每个特征Xi与Y的对称不确定性,计算公式为
| $ S{U_{\max }}\left( {{X_i};Y} \right) = 2\left[ {\frac{{{I_{{\text{max}}}}\left( {X;Y} \right)}}{{H\left( {{X_i}} \right) + H\left( Y \right)}}} \right] $ | (6) |
最后,进行SUmax(Xi; Y)的排序,SUmax(Xi; Y)值大的排在前面,说明排在前面的特征重要性高.
3.2 冗余性分析依照近似马尔可夫毯的条件进行冗余特征的删除.具体条件公式为Imax(Xi; Y)>Imax(Xj; Y)并且Imax(Xj; Y) < Imax(Xi; Xj).
通过上面条件判断,最终得到最优的特征子集Soption.其中Xi∈S,Xj∈S(i≠j).
算法1 NFCBF算法描述
1 Initization: Soption=ϕ, S=ϕ, T
2 Calculate Imax(X; Y), for each Xi∈T
3 Calculate SUmax(Xi; Y), for each Xi∈T
4 sorted SUmax(Xi; Y), orderby= Descending and S←{Xi}, for each Xi∈T
5 while S≠ϕ
if Imax(Xi; Y)>Imax(Xj; Y)
and Imax(Xj; Y) < Imax(Xi; Xj)
remove Xi
6 output the selected set Soption of features.
步骤1 初始化特征集合T、Soption和S.其中,T代表全集;
步骤2 计算原始特征集合T中的每个特征Xi与Y最大信息系数Imax(X; Y);
步骤3 计算每个特征Xi与Y之间的对称不确定性值SUmax(Xi; Y);
步骤4 对这些SUmax(Xi; Y)进行排序,并且将排序好的特征Xi存入S集合中;
步骤5 按照近似马尔可夫毯条件,进行冗余特征的删除;
步骤6 得到最优的Soption集合.
4 实验结果与分析 4.1 实验工具和数据处理仿真软件为python2.7.12.实验数据集选择了国际著名的UCI通用数据集,见表 1.
|
|
表 1 UCI中的8个常用数据集 |
采用两种分类器方法来构建预测模型:朴素贝叶斯分类器(Naïve Bayes)[11]和k近邻(KNN)分类器[12]都是预测分类准确率最为常见的分类器.近邻分类器选择3近邻的参数,朴素贝叶斯分类器选择默认参数设置.
4.2.2 特征选择方法为了论证NFCBF算法的有效性,选择了3类有代表性特征选择算法,作为NFCBF算法的比较对象. 1) FullSet算法就是指不做任何特征选择和排序;2)MIM算法和FCBF算法;3)最少的绝对收缩和选择算法(Lasso)和岭算法(Ridge).
4.3 分类准确性实验为了进一步验证NFCBF算法在所得最优特征子集的分类性能.本次实验首先在UCI中8个数据集上采用10折交叉法将所有样本随机分为均匀的10等分,每次随机将其中一组当作测试样本集合进行测试,其余9组当作训练样本集合,分别使用FullSet、NFCBF、MIM、FCBF、Lasso和Ridge算法,从训练集中选出最优特征子集,并将选择出特征子集放到测试集进行测试.实验中依次在KNN分类器和Naïve Bayes分类器中进行实验.为了使实验更具有公平性,重复实验过程10次,然后对这10次实验结果求均值,得到实验结果如表 2~表 3.为了更好的说明分类准确率,表 2~表 3给出了具体的分类准确率数值并在它旁边都附加了特征数.
|
|
表 2 KNN分类器下分类准确率比较 |
|
|
表 3 Native Bayes分类器下分类准确率比较 |
从表 2可知,NFCBF算法在第3、第4和第7分类效果最好.在第1、第2和第3中,NFCBF算法与FCBF算法选择出特征数实现的分类效果一样好.特别是在第3个数据集中,NFCBF算法所选择的特征数要少于FCBF算法所选择出的特征数.在第6个数据集上,它与最佳分类效果之间的差距只有0.5%.这种差距已经非常小,几乎可以忽略不计了.从表 3中,可以知道,NFCBF算法在第5、第7和第8分类效果最好.在第3个数据集中,NFCBF算法和FCBF算法最好.在第6个数据集中,NFCBF算法和FCBF算法、Lasso、MIM算法分类效果一样好,其中在第3个数据集上,它所选择出的特征子集明显少于FCBF算法选择出的特征数.在第2个数据集上,它与最佳分类效果之间的差距只有0.5%,这种差距已经非常小,几乎可以忽略不计.同时,本实验给出不同特征选择算法在不同分类器上部分显示效果图,如图 1~图 4所示.
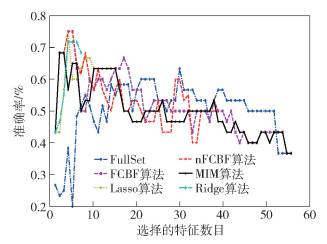
|
图 1 在KNN和lung-cancer中不同算法准确率比较 |

|
图 2 在KNN和ionosphere中不同算法准确率比较 |
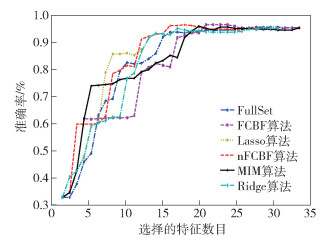
|
图 3 在Naïve Bayes和dermatology中不同算法准确率比较 |
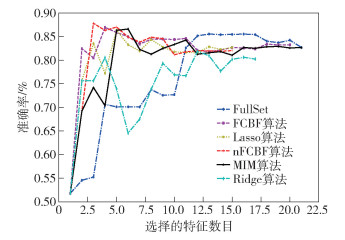
|
图 4 在Naïve Bayes和mushroom中不同算法准确率比较 |
本文通过最大相关信息系数理论与方法改进了FCBF算法,构建了特征相关性排序和删除冗余性特征两阶段特征选择算法NFCBF算法,在UCI中8个公开的数据上进行了实验对比分析发现,在KNN分类器中,NFCBF算法所选择出特征数比FullSet特征数平均少了30.75个,分类准确率平均提高了2.061 25%;在Naïve Bayes分类器中,NFCBF算法所选择出特征数比FullSet特征数平均少了27.13个,分类准确率平均提高了0.176 25%;在KNN分类器中,NFCBF算法所选择出特征数比FCBF算法所选择特征数平均少了2.5个,分类准确率平均提高了0.067 5%;在Naïve Bayes分类器中,NFCBF算法所选择出特征数比FCBF算法所选择特征数平均少了4.75个,分类准确率平均提高了0.081 25%.通过上面的分析,NFCBF算法在绝大多数数据集上表现优秀,不管是在分类准确率还在是特征数的选择上均优于FCBF算法、MIM算法和FullSet,同时,在分类准确率方面,在绝大多数数据集上,NFCBF算法优于Lasso算法和Ridge算法.
下一步将把NFCBF算法引入分布式算法和数据驱动算法中,通过两阶段特征选择算法进一步优化分布式算法和数据驱动算法;同时,在更大样本集和更高特征数的集合中进行特征相关性和特征冗余性的分析与研究,并进一步优化和丰富最大相关信息系数理论和近似马尔可夫毯方法.
| [1] | Lynch C. Big data:How do your data grow?[J]. Nature, 2008, 455(7209): 28–29. doi: 10.1038/455028a |
| [2] | Jain A K, Duin R P W, Mao J. Statistical pattern recognition:a review[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(1): 4–37. |
| [3] | Bennasar M, Hicks Y, Setchi R. Feature selection using joint mutual information maximisation[J]. Expert Systems with Applications, 2015, 42(22): 8520–8532. doi: 10.1016/j.eswa.2015.07.007 |
| [4] | Kwak N, Choi C H. Input feature selection for classification problems[J]. IEEE Transactions on Neural Networks, 2002, 13(1): 143. doi: 10.1109/72.977291 |
| [5] | Peng H, Long F, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2005, 27(8): 1226–1238. |
| [6] | Zhang Y, Yang C, Yang A, et al. Feature selection for classification with class separ-ability strategy and data envelopment analysis[J]. Neurocomputing, 2015, 166(C): 172–184. |
| [7] | Sotoca J M, Pla F. Supervised feature selection by clustering using conditional mutual information-based distances[J]. Pattern Recognition, 2010, 43(6): 2068–2081. doi: 10.1016/j.patcog.2009.12.013 |
| [8] | Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334(6062): 1518–1524. doi: 10.1126/science.1205438 |
| [9] | Yu L, Liu H. Eficient feature selection via analysis of relevance and redundancy[J]. Journal of Machine Learning Research, 2004, 5(12): 1205–1224. |
| [10] | Novakovié, Jasmina, Strbac, et al. Toward optimal feature selection using ranking methods and classification algorithms[J]. Yugoslav Journal of Operations Research, 2011, 21(1): 119–135. doi: 10.2298/YJOR1101119N |
| [11] | Brown G, Pocock A, Zhao M J, et al. Conditional likelihood maximisation:a unifying framework for information theoretic feature selection[J]. Journal of Machine Learning Research, 2012, 13(1): 27–66. |
| [12] | Qiao J. On the preimages of parabolic periodic points[J]. Nonlinearity, 2000, 13(3): 813–818. doi: 10.1088/0951-7715/13/3/316 |
| [13] | Cover T M, Thomas J A. Elements of information theory[M]. Tsinghua University Press, 2003. |
| [14] | Wong T T. A hybrid discretization method for naïve Bayesian classifiers[J]. Pattern Recognition, 2012, 45(6): 2321–2325. doi: 10.1016/j.patcog.2011.12.014 |
| [15] | Robnik-Sikonja M, Kononenko I. Theoretical and empirical analysis of relief and relieff[J]. Machine Learning, 2003, 53(1-2): 23–69. |


