针对实际工程中小子样结构机构可靠性分析的问题,提出了Bootstrap—支持向量回归(SVR)—二阶累计量(SOC)方法框架和多阶矩虚拟样本容量扩充方法,增强了扩充后样本的客观性;将Bootstrap与SVR方法结合,构建出结构机构可靠性极限状态函数,并利用SOC方法计算可靠度指标.最后,应用摆动导杆机构的仿真算例验证了新方法的有效性.
In order to solve the small sample reliability problems for structures and mechanisms in real applications, an analyzing framework named Bootstrap-support vector regression-second order cumulant (Bootstrap-SVR-SOC) method together with a sample size extension method combining multi-order moments that could make the extended samples more objective were proposed. Bootstrap was combined with support vector regression method in order to build the limit state function for reliability analysis based on the second order cumulant approach. Finally, numerical case of a crank shaper mechanism was analyzed to demonstrate the effectiveness of the proposed framework.
近年来,结构机构可靠性问题日益突出[1],并逐渐成为可靠性研究领域内的热点.一些针对结构机构可靠性分析的理论方法相继被提出[2-4].通常情况下,结构机构可靠性分析会涉及复杂、隐式的极限状态方程,对此,各类行之有效的响应面方法[5]也被相继提出.然而,在航空、航天、型号工程等领域,由于试验条件及试验成本的限制,结构机构的某些基本设计变量通常仅能够获得少量或极少量样本,致使其可靠性研究成为小子样或极小子样问题.上述各类分析方法均以已知基本变量的完备统计信息为前提,无法直接解决广泛存在的小子样或极小子样结构机构可靠性分析问题.笔者提出了适用于含小子样、极小子样基本变量结构机构可靠性分析的方法框架.在充分利用相似产品的方差、偏度、峰度以及中位数—均值比等多种统计信息的基础上,提出多阶矩样本容量扩展方法(以下简称“扩容”),并利用二阶累积量(SOC, second order cumulant)方法计算得出相应的可靠度系数,避免了迭代求解.最后,借助摆动导杆机构算例对该方法的有效性进行了验证.
1 多阶矩虚拟样本容量扩展方法 1.1 虚拟样本增广方法令n为结构机构基本变量的试验样本量,S代表试验样本均值(当n=1时,近似取S=S0,S0为一次试验样本值),根据相似经验得知设计变量(以下简称“经验变量”)近似服从正态分布,黄玮等[6]建议按式(1)的形式进行设计变量的样本增广:
| $ S = \bar S \pm \left( {\alpha {{\left( {i - 1} \right)}^\beta } + \xi } \right)\sigma ,i = 1,2, \cdots ,k/2 $ | (1) |
其中:S为增广后的设计变量样本,S和经验变量的样本标准差σ为已知参数;α和β为控制参数, 由人为主观确定;ξ为待定系数;k为设计变量增广后的样本容量.待定系数ξ依据如下原则进行计算:增广后的设计变量样本均值等于试验样本均值,增广后的设计变量样本方差等于经验变量方差.由上述原则,有如下方程组:
| $ \left. \begin{array}{l} \frac{{\bar S + \sum\limits_{i = 1}^k {{S_i}} }}{{k + 1}} = \bar S\\ \frac{{\sum\limits_{i = 1}^k {{{\left( {{S_i} - \bar S} \right)}^2} + {{\left( {{S_{13}} - \bar S} \right)}^2}} }}{k} = {\sigma ^2} \end{array} \right\} $ | (2) |
将样本S1~S12代入式(2),求得待定系数ξ.
1.2 多阶矩虚拟样本容量扩展方法由式(1)(2)可以看出,黄玮等[6]所采用的虚拟增广样本方法对于经验变量近似服从正态分布的情况具有较好的适用性,由于该方法采用对称形式进行样本扩容,所以对于经验变量服从偏态分布的情况,实施效果并不理想.此外,式(1)中扩容控制参数α、β需要人为主观确定,也在很大程度上限制了该方法的合理性和实用性,关键步骤如下:
1) 借鉴式(1),采用非对称样本扩容控制方程,使得所提出的方法不仅适用于经验变量服从正态分布的情况,对于偏态分布也具有较好的适用性;
2) 引入经验变量的偏度、峰度以及中位数等统计量,确定扩容控制方程中的未知参数.
结合Bootstrap方法,建议将设计变量样本量增至13个以上[6],假设试验样本量为n0=1,增容后的样本量为k=15,采用式(3)(4)进行样本扩容.
| $ {S_{{\rm{Ⅰ}} - i}} = \bar S + \left( {{\alpha _{\rm{Ⅰ}}}{{\left( {i - 1} \right)}^{{\beta _{\rm{Ⅰ}}}}} + \xi } \right)\sigma ,i = 1,2, \cdots ,k/2 $ | (3) |
| $ {S_{{\rm{Ⅱ}} - i}} = \bar S + \left( {{\alpha _{{\rm{Ⅱ}}}}{{\left( {i - 1} \right)}^{{\beta _{{\rm{Ⅱ}}}}}} + \xi } \right)\sigma ,j = 1,2, \cdots ,k/2 $ | (4) |
其中:SⅠ、SⅡ为扩容后设计变量样本,试验样本均值S以及经验变量样本标准差σ为已知参数,αⅠ、αⅡ以及βⅠ、βⅡ为扩容控制参数,ξ是待定系数.
依据式(3)(4),可知扩容后的样本为
假设经验变量服从某一偏态分布(正态分布的偏度为0,峰度为3),依据如下原则确定式(3)(4)中的未知参数:
1) 扩容后的样本均值等于设计变量试验均值;
2) 扩容后的样本方差等于经验变量方差;
3) 扩容后的样本偏度等于经验变量偏度;
4) 扩容后的样本峰度等于经验变量峰度;
5) 扩容后的样本中位数与均值之比等于经验变量中位数与均值之比.
由上述原则,可列出式(5).
| $ \left. \begin{array}{l} \frac{1}{{k + 1}}\left( {{S_0} + \sum\limits_{i = 1}^{k/2} {{S_{{\rm{I}} - i}}} + \sum\limits_{j = 1}^{k/2} {{S_{{\rm{II}} - j}}} } \right) = \bar S\\ \frac{1}{k}\left[ {\sum\limits_{i = 1}^{k/2} {{{\left( {{S_{{\rm{I}} - i}} - \bar S} \right)}^2}} + \sum\limits_{j = 1}^{k/2} {{{\left( {{S_{{\rm{II}} - j}} - \bar S} \right)}^2} + {{\left( {{S_0} - \bar S} \right)}^2}} } \right] = {\sigma ^2}\\ \frac{{{k^3}\left[ {\sum\limits_{i = 1}^{k/2} {{{\left( {{S_{{\rm{I}} - i}} - \bar S} \right)}^4}} + \sum\limits_{j = 1}^{k/2} {{{\left( {{S_{{\rm{II}} - j}} - \bar S} \right)}^4} + {{\left( {{S_0} - \bar S} \right)}^4}} } \right]}}{{{{\left[ {\sum\limits_{i = 1}^{k/2} {{{\left( {{S_{{\rm{I}} - i}} - \bar S} \right)}^2}} + \sum\limits_{j = 1}^{k/2} {{{\left( {{S_{{\rm{II}} - j}} - \bar S} \right)}^2} + {{\left( {{S_0} - \bar S} \right)}^2}} } \right]}^3}}} - 3 = Kt\\ \frac{{{k^2}\left[ {\sum\limits_{i = 1}^{k/2} {{{\left( {{S_{{\rm{I}} - i}} - \bar S} \right)}^3}} + \sum\limits_{j = 1}^{k/2} {{{\left( {{S_{{\rm{II}} - j}} - \bar S} \right)}^3} + {{\left( {{S_0} - \bar S} \right)}^3}} } \right]}}{{{{\left[ {\sum\limits_{i = 1}^{k/2} {{{\left( {{S_{{\rm{I}} - i}} - \bar S} \right)}^2}} + \sum\limits_{j = 1}^{k/2} {{{\left( {{S_{{\rm{II}} - j}} - \bar S} \right)}^2} + {{\left( {{S_0} - \bar S} \right)}^2}} } \right]}^{3/2}}}} = Sk\\ {S_{\left( {\frac{{k + 1}}{2}} \right)}} = m \end{array} \right\} $ | (5) |
其中:Kt为经验变量的峰度,Sk为经验变量的偏度,S(
采用数值方法求解式(5),即可得出式(3)(4)中的未知参数.应注意到,式(5)可能存在多组可行解,建议依据下述原则选择适合的实数解:
所获得的实数解使得所生成的样本SⅠ-1~SⅠ-7以及SⅡ-1~SⅡ-7较为平均地分布在均值S的两侧.
2 小子样结构机构可靠性分析的BoSS方法框架适用于小子样、极小子样结构机构可靠性分析的BoSS方法框架步骤如下:
1) 结合经验变量的统计信息,利用第2节所提出的多阶矩样本容量扩展方法增广结构机构中小子样或极小子样设计变量的样本容量.令各小子样设计变量为Xi(i=1, 2, …, M),进行样本扩容后,各设计变量的经验分布为Fi*(θi)(i=1, 2, …, M),其中θi(i=1, 2, …, M)为各经验分布中的未知参数向量.
2) 利用扩充样本,采用Bootstrap方法“提携”样本容量,并对θi进行参数估计,用含有Bootstrap统计量的经验分布Fi*(
3) 基于各设计变量的分布,采用拉丁超立方抽样方法对结构机构各个设计变量进行抽样,进而结合有限元法、机构动力学等理论方法,将结构机构物理属性加以充分考虑,利用设计变量的抽样值计算对应的结构机构响应.最后将结构机构的各个设计变量和计算得到的响应进行当量正态化及标准正态化.
4) 在标准正态空间中,选取步骤3)中得出的部分样本及其响应,利用非线性支持向量回归(SVR, support vector regression)方法拟合得出结构机构响应与各设计变量间的函数关系,即
| $ G = G\left( \mathit{\boldsymbol{X}} \right) $ | (6) |
其中X=[X1, X2, …, XM]T为设计变量向量.
为保证结构机构处于可靠工作状态,系统响应
| $ \left| {G\left( \mathit{\boldsymbol{X}} \right)} \right| < \lambda $ | (7) |
其中λ>0是系统响应安全阈值.
若结构机构能完成规定的功能,则系统一定处于安全工作状态.因此可以表示出结构机构相应的可靠性极限状态函数为
| $ g\left( \mathit{\boldsymbol{X}} \right) = \lambda - \left| {G\left( \mathit{\boldsymbol{X}} \right)} \right| $ | (8) |
5) 利用SOC方法[7]计算可靠度指标.
若各设计变量服从正态分布,则结构机构系统响应的前二阶矩可表示为
| $ \begin{array}{*{20}{c}} {{\mu _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,1}} = 2{\sigma _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|}}\phi \left( {\frac{{{\mu _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,1}}}}{{{\sigma _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|}}}}} \right) + }\\ {{\mu _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,1}}\left( {1 - 2\mathit{\Phi }\left( { - \frac{{{\mu _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,1}}}}{{{\sigma _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|}}}}} \right)} \right)} \end{array} $ | (9) |
| $ {\mu _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,2}} = \mu _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,1}^2 + \sigma _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|}^2 $ | (10) |
则系统极限状态函数前二阶累积量为
| $ {\kappa _{g,1}} = {\kappa _{\lambda ,1}} - {\kappa _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,1}} $ | (11) |
| $ {\kappa _{g,2}} = {\kappa _{\lambda ,2}} - {\kappa _{\left| {G\left( \mathit{\boldsymbol{X}} \right)} \right|,2}} $ | (12) |
由可靠度指标的定义可知
| $ \beta = \frac{{{\mu _g}}}{{{\sigma _g}}} = \frac{{E\left[ {g\left( \mathit{\boldsymbol{X}} \right)} \right]}}{{\sqrt {{\rm{Var}}\left[ {g\left( \mathit{\boldsymbol{X}} \right)} \right]} }} = \frac{{{\kappa _{g,1}}}}{{{\kappa _{g,2}}}} $ | (13) |
SOC方法避免了可靠度指标的迭代求解,提高了可靠性分析的效率.
6) 将其余样本分组,重复步骤(4)(5),对可靠度指标进行迭代更新,直到达到规定的收敛精度δ.
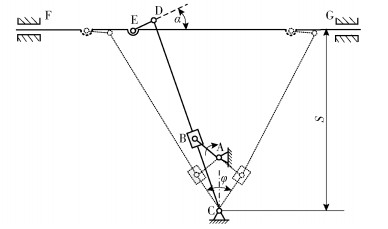
3 仿真算例 3.1 算例概述以某型号机床的主传动机构运动精度可靠性分析为例,对笔者所提出的Bootstrap-SVR-SOC框架有效性进行验证,机构简图如图 1所示.其中:曲柄AB的设计长度为75 mm,摇杆CD的设计长度为480 mm,滑块B在摇杆CD上滑动,连杆DE公称长度为150 mm,FG在机架上做平动,S=255 mm,曲柄AB的转速为5 r/min,摇杆CD的摆角φ=180°×(K-1)/(K+1),K为行程速比,此例中取K=2.机构主要参数如表 1所示.为突出笔者所提方法,假设由于制造成本所限,摇杆CD仅有1个样本.以工作过程中连杆DE的最大压力角α小于等于60°为目标,建立机构性能极限状态函数,并进行可靠性分析.
|
图 1 传动机构简图 |
|
|
表 1 传动机构参数 |
1) 利用所提出的多阶矩样本容量扩展方法,获得摇杆CD长度LCD的经验分布.假设由经验得知类似零件长度近似服从对数正态分布,标准差为0.46,偏度系数为2.54,峰度系数为1.65,中位数与均值之比为1.37.根据式(5)得出相应的控制参数如表 2所示.
|
|
表 2 样本扩容控制参数计算值 |
利用表 2中求出的控制参数,根据式(3) (4)得出扩展后的LCD各样本如下:
以上各式中,S=480 mm,σ=0.46 mm,结合表 1所得出的LCD各虚拟样本数值见表 3.
|
|
表 3 扩展所得LCD虚拟样本值 |
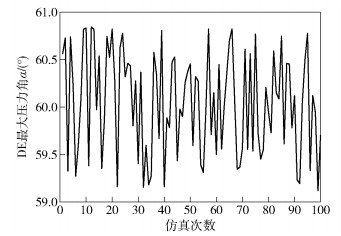
2) 采用文献[8]中提出的方法产生服从扩展后LCD样本经验分布的100个随机样本点,并采用拉丁超立方抽样方法进行设计变量的随机抽样.在Adams-Insight软件中考虑各杆件柔性的机构动力学仿真,得出的连杆DE工作过程最大压力角变化范围如图 2所示.
|
图 2 连杆DE最大压力角α的仿真结果 |
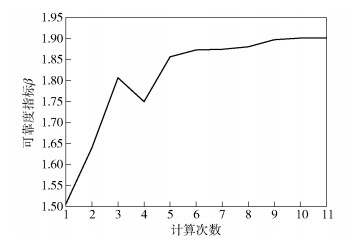
3) 抽取前50组设计变量样本及对应的连杆DE压力角仿真结果,利用Matlab-LSSVMLAB拟合响应与设计变量的函数关系,结合SOC方法计算可靠度指标β0.将剩余50组数据分为10组,依据Bootstrap-SVR-SOC方法对指标进行逐次更新,规定收敛精度δ=0.1.各次计算得出的可靠度指标参见表 4,指标更新变化情况如图 3所示.
|
|
表 4 计算所得可靠度指标 |
|
图 3 可靠度指标更新过程 |
1) 由表 3可以看出,扩展所得的LCD虚拟样本值较为对称地分布在实际样本值482 mm的两侧,分布情况良好.
2) 因算例属于极小子样可靠性问题,很难实现理论意义上的高可信性分析,但从无偏性、客观性角度出发,依据所提方法生成的虚拟样本较为合适.
3) 由表 4可以看出,进行5次更新计算后,可靠度指标即收敛到规定的精度范围;进行8次更新计算后,可靠度指标稳定在1.90附近(对应的可靠度为0.971 3);第4次计算后可靠度指标下降的原因在于补充样本的随机性.计算结果说明Bootstrap-SVR-SOC方法框架具有较好的稳定性.
4 结束语提出了小子样、极小子样设计变量的多阶矩虚拟样本容量扩展方法,充分利用了相似产品的方差、偏度、峰度、中位数—均值比等统计信息,针对难以做出理论上高可信度可靠性分析预测的情况,提供了一种较为合理、客观的实现途径.将Bootstrap、SVR、SOC方法相结合,并充分利用有限元、机构动力学等理论方法,基于所提出的多阶矩虚拟样本容量扩充方法形成了适用于小子样结构机构可靠性分析的Bootstrap-SVR-SOC方法框架,利用摆动导杆机构最大工作压力角可靠性仿真算例验证了方法的合理性. Bootstrap-SVR-SOC方法充分考虑结构机构的物理背景,相较于单纯从数据角度进行分析预测的事后评估方法,具有较好的工程实用价值.
| [1] |
张义民. 机械可靠性设计的内涵与递进[J]. 机械工程学报, 2010, 46(14): 167–188.
Zhang Yimin. Connotation and development of mechanical reliability-based design[J]. Journal of Mechanical Engineering, 2010, 46(14): 167–188. |
| [2] | Ditlevsen O, Madsen H O. Structural reliability methods[M]. New York: Wiley, 1996. |
| [3] | Der Kiureghian A, Dakessian T. Multiple design points in first and second-order reliability[J]. Structural Safety, 1998, 20(1): 37–49. doi: 10.1016/S0167-4730(97)00026-X |
| [4] | Aslett Louis J, Nagapetyan Tigran, Vollmer Sebastian J. Multilevel Monte Carlo for reliability theory[J]. Reliability Engineering and System Safety, 2017(165): 188–196. |
| [5] | Huang Xianzhen, Liu Yang, Zhang Yimin, et al. Reliability analysis of structures using stochastic response surface method and saddlepoint approximation[J]. Struct Multidisc Optim, 2017(55): 2003–2012. |
| [6] |
黄玮, 冯蕴雯, 吕震宙. 极小子样试验的虚拟增广样本评估方法[J]. 西北工业大学学报, 2005, 23(3): 384–387.
Huang Wei, Feng Yunwen, Lu Zhenzhou. Virtually expanded sample estimation method for extremely small-scale sample test[J]. Journal of Northwestern Polytechnical University, 2005, 23(3): 384–387. doi: 10.3969/j.issn.1000-2758.2005.03.024 |
| [7] | Iglesias M C, Manteiga W G. Bootstrap for conditinal distribution function with truncated and censored data[J]. Annual Institute Statistic Math, 2003, 55(2): 331–357. |
| [8] | Qiu Jiwei, Zhang Jianguo, Ma Yupeng, et al. Reliability-based robust design for kinematic accuracy of a mechanism with axiomatic theory[EB/OL]. (2017-06-09)[2017-11-11]. 2017. https: //doi. org/10. 1177/0954410017714005. |


