2. 浪潮集团有限公司 高效能服务器和存储技术国家重点实验室, 北京 100085
以现场可编程门阵列(FPGA)为核心构建了高性能、高密度异构加速卡.基于目标阻抗设计方法,对解耦电容和电路进行了交流和直流分析,并给出了电源完整性后仿结果,验证了该分析方法的有效性.最后给出了该FPGA异构加速卡在图像识别中的应用实例,并与中央处理器、图形处理器的性能作了对比.
2. State Key Laboratory of High-End Server and Storage Technology, Inspur Group Company Limited, Beijing 100085, China
A high performance and high density field programmable gate array (FPGA) heterogeneous accelerate board was proposed. Base on target impedance design method, the AC/DC characteristics were analyzed and power integrity post simulation was present. Application on image identification utilized the proposed heterogeneous FPGA accelerate board and performance comparison are given.
当今,各种应用逐步向云环境迁移,现场可编程门阵列(FPGA,field programmable gate array)因其强大的并行计算能力正在成为新型的行业解决方案. FPGA异构加速卡是一种异构计算平台的体系结构,通过并行和流水等设计手段,可提高计算能力、能效比和计算实时性,对应用进行硬件加速处理.
图 1所示为基于高速串行计算机扩展总线(PCIe,peripheral component interconnect express)的FPGA异构加速卡实物图.该加速卡系统核心为一片FPGA芯片,其余芯片主要包括:1片复杂可编程逻辑器件(CPLD,complex programmable logic device);2个双倍速率SDRAM(DDR4,double data rate SDRAM)内存通道;PCIe Gen3.0x8 Lane;两路光口(SFP+,small form-factor pluggables);2片NOR FLASH芯片数据级联,用于FPGA的FPP配置;1片1Gb QSPI串行NOR FLASH,用于FPGA的AS配置;1片板载512Kb EEPROM,用于存储板卡信息.该FPGA异构加速卡为16层PCB设计,具有极高的密度.

|
图 1 加速卡实物图 |
随着封装集成及半导体技术的发展,单芯片中集成的晶体管数量越来越多,与此同时,芯片的供电电压和电压噪声容限不断减小,电路功耗不断增加,这使得电源完整性(PI,power integrity)问题日显突出.随着集成电路向更高集成度、更低电压及更高功耗的趋势发展,PI问题已逐渐成为高速电子系统设计的重点.事实上,很多产品研发和生产仍然完全依赖工程师的经验进行印刷电路板(PCB,printed circuit board)的设计和投板,这种研发流程无疑会给生产成本和投产周期带来风险.若在投板之前利用电源完整性仿真软件对设计进行仿真验证,则可在很大程度上提高设计的可靠性,降低成本并缩短研发周期,大大提高板卡产品的成品率.
基于FPGA异构加速卡,对PCB设计中的电源完整性问题进行了分析和仿真.
1 电源完整性分析随着集成电路电源电压不断降低,芯片内部开关器件数目不断增加,在设计中已经不能将电源电压和地电压假定为绝对稳定状态,电源电压或者地电压的波动会给高速电路系统带来致命影响.在高速系统中,电源分配网络的输入阻抗随频率的变化而变化,导致PCB电源/地平面上出现由同步开关噪声电流、瞬态负载电流引起的同步开关噪声电压,造成供电不连续,严重影响高速系统的正常工作[1-2].
1.1 PDN与目标阻抗本设计中,电源纹波的影响主要体现在FPGA的电源引脚上,过大的电源纹波将影响PCB电压的稳定性.在理想电压源中,输出的电压是恒定的,然而在实际的电源分配网络中,输入阻抗的影响不可忽略.如果能够在电源与芯片之间建立一个比较完善的电源分配网络,就可以在一定时间内为芯片提供足够的驱动电流. 图 2所示为一个典型的电源分配网络,这种设计方法将电源分配网络(PDN,power distribution network)看作一个系统,电源分配网络被平均电流激励,当电流噪声和瞬态电流通过PDN时,可能会引起电压噪声,引起供电中断.利用目标阻抗的方法对电源分配网络进行设计,使宽带内电源阻抗小于目标阻抗[3-4].为满足电路系统对电源的要求,目标阻抗可通过式(1)计算.
| $ {{Z}_{\text{target}}}=\frac{{5\% V}}{I} $ | (1) |
其中:V为标准电源电压,5%V为电源噪声容限,I为芯片工作电流,计算中通常为芯片最大工作电流的50%(保守值)或30%(典型值).
当晶体管开关电路需要电流对负载充电时,这个电流由PDN来提供.当电压调节模块由于其高输出阻抗而不能及时做出反应时,就需要有其他电源来提供电流从而维持电压.由于电容能够储存电荷,可直接为晶体管开关电路供电.旁路电容也可称为解耦电容,可以为电源转换芯片和开关电路解耦.根据解耦电容的工作范围及其与晶体管开关电路的靠近程度,可将解耦电容分为高频电容、中频电容和低频电容,如图 2所示.低频解耦电容可以选用大容量的电解电容来维持低的PDN输入阻抗;中频、高频解耦电容可以选用不同的介质及不同尺寸制成的陶瓷电容器.通过图 2中展示的PDN频率—阻抗曲线,可以容易的看出在哪些频率上将会产生比较严重的电源噪声.这种设计方法可以很好的运用PDN对信号完整性(SI,signal integrity)及电磁干扰(EMI,electromagnetic interference)的影响进行分析和设计,因此目标阻抗法是电源分配网络PDN设计的典型方法[5].

|
图 2 典型电源分配网络 |
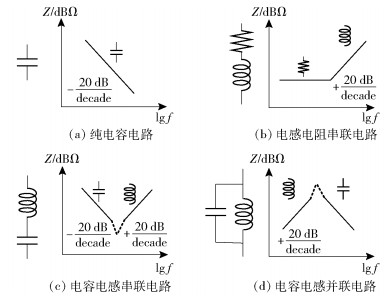
在对解耦电容分析之前,首先应了解几种常见电路模型的频率响应.假设角频率为ω,电容器静电容量为C,则理想状态下电容器的阻抗Z可由式Z=1/(jωC)计算,由该式可知,理想电容阻抗随频率增加反比例减小,如图 3(a)所示.假设电感值为L,则理想状态下电感阻抗Z可由式Z=jωL计算,由该式可知,理想电感阻抗随频率增加而增大,如图 3(b)所示.电容电感串联电路,等效阻抗为Z=jωL+1/(jωC)=j(ωL-1/(ωC)),该式中虚部用X表示,当X=0时,电路处于谐振状态,此时容抗感抗相互抵消,电路阻抗最小,如图 3(c)所示.反之,电容电感并联,谐振状态下电路阻抗最大,频率响应如图 3(d)所示.
|
图 3 不同电路模型频率响应 |
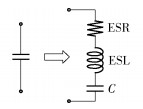
实际电容器模型如图 4所示[6],C为理想电容,ESR为等效串联电阻,ESL为等效串联电感.该电容阻抗可由式(2)计算.
|
图 4 实际电容模型 |
| $ Z=R+\text{j}\omega L+\frac{1}{\text{j}\omega C} $ | (2) |
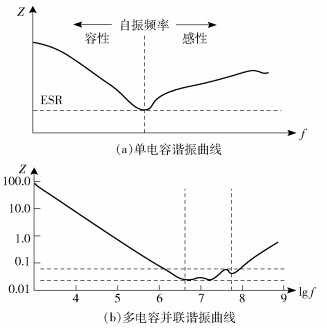
由式(2)可知:在低频段(jωL≪1/jωC),电容对外表现为电容特性;在高频段,(jωL≫1/jωC),电容对外表现为电感特性;当jωL=1/jωC时,即ω=1/LC,此时容性阻抗与感性阻抗相抵,该电容阻抗最小,对外表现为纯阻特性,该频率点称为电容的自谐振频率,图 5(a)所示为单电容谐振曲线.结合对图 3的分析可知,当电容器对外表现为电感特性时,电容就失去了解耦效果.因此,解耦电容都存在各自的解耦频率范围,只有在其工作频率范围内,电容才具有很好的解耦作用.
|
图 5 电容谐振曲线 |
不同封装的电容器有不同的谐振频率,表 1、表 2列出了不同封装下电容参数以及同一封装下电容的谐振频率.选用0805-1 μF、0603-0.1 μF及0402-0.01 μF的电容并联,所得频率—阻抗曲线如图 5(b)所示.采用以上电容并联后,可以得到一个较宽的低阻抗频带,4.224~58.746 MHz,阻抗维持在23.318~61.340 mΩ,达到了展宽低阻抗频带的目的[7].因此,在采用不同的封装和容值的电容并联后,可以展宽低阻抗频带.在高速电路设计中,噪声等相关的干扰往往不是处在一个频点上,而是占据一段频带.在实际的高速电路设计中,期望准确的定位电路上的每一处的噪声频带很不现实,通过将多种不同封装、不同容值的电容并联可得到一个比较宽的低阻抗频带,从而尽可能的覆盖电路设计中的噪声频带.
|
|
表 1 不同封装电容参数 |
|
|
表 2 相同封装不同容值电容谐振频率值 |
在多层PCB中,电源层为由导电材料如铜构成的平面结构.器件的电源引脚连接到电源线路上,电源线路通过通孔连接到电源平面.由于传输线或者通孔存在阻抗,在电源引脚和器件电源引脚之间会存在电压降落,因此实际器件电源电压将低于标称值,过高的电压降落被称作“轨道塌陷”,这种情况会导致器件电源电压低于芯片需要的最小电压,造成电路故障[8-9].直流压降分析计算了由电源模块引脚到其他电路芯片引脚的电压降落.在该分析中,仿真工具从复杂的PCB物理结构创建了精确的电阻模型. 表 3所示为该PCB 0.95 V电源平面直流后仿真结果.
|
|
表 3 电源完整性直流仿真结果 |
对0.95 V电源平面进行直流压降仿真,该电源平面最小电压为0.936 V(>0.95 V×95%),满足设计要求.
表 4所示为铜厚为1/2 oz时印刷电路板布线标准MIL-STD-275.由该标准PCB载流数据可知,当线宽增大,铜箔厚度增加时,PCB的载流能力也相应增强,计算PCB极限电流密度的经验式为
| $ 电流密度=\frac{电流}{铜箔厚度\times 线宽} $ | (3) |
|
|
表 4 印刷电路板布线标准(铜厚1/2 oz) |
在本PCB设计中,线宽为0.25 inch,铜箔厚度为0.017 8 mm,由式(3)可知,该PCB最大电流密度为7.2 A/(0.0178×(0.25×25.4))=63.7 A/mm2.
对0.95 V电源平面电流密度进行后仿真得到该电源平面最大电流密度分别为36.5 A/mm2和51.2 A/mm2,满足设计要求.
2.2 交流分析交流分析的目的是降低电流的瞬态行为引起的电压波动,其度量标准是电源分配网络阻抗.电源网络阻抗应在带宽范围内维持在较低的值以保证电源噪声在芯片允许的范围内.在目标阻抗设计方法中,电源平面阻抗应保持低于目标值,超过目标值会导致PDN中的高噪声.
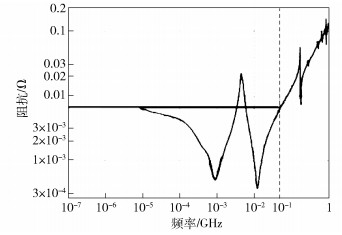
本设计中,0.95 V电源轨道上允许的最大波动电压为5%,最大瞬态电流为6.78 A,由式(1)可知,目标阻抗为7 mΩ.对0.95 V电源分配网络进行交流仿真,得到图 6所示的0.95 V电源平面阻抗分布曲线.由图可知,在关心的频段内,平面阻抗高于目标阻抗,针对该问题,对解耦网络进行了优化.
|
图 6 阻抗分布曲线 |
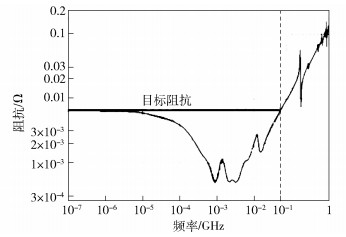
在原来的解耦电容网络中增加C207、C210、C213三个330 μF解耦电容,重新做PDN网络阻抗仿真,阻抗结果如图 7所示,增加解耦电容网络后,阻抗下降到目标阻抗之下,满足设计要求.
|
图 7 优化后阻抗分布曲线 |
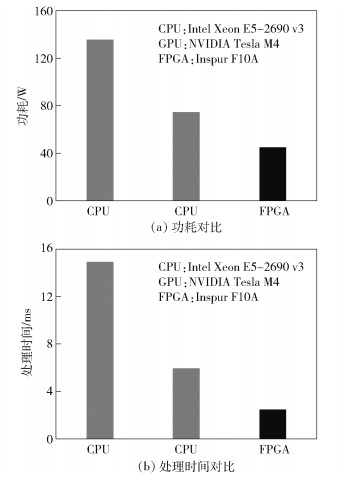
利用本设计的FPGA异构加速卡,搭建了图像处理系统,通过硬件算法实现了图像的流水线及并行处理和对特定物体的识别.单机单卡下运行ResNet模型,输入图片尺寸为32×32的情况下,吞吐量为311 fps,Top-1准确率为92.3%,Top-5准确率为99.6%. 图 8所示为FPGA加速卡与CPU、GPU在功耗和处理时间上的性能对比(CIFAR-10数据集,ResNet57),结果显示,相比于CPU、GPU,该FPGA异构加速卡在更低的功耗下具有更高的速度.
|
图 8 CPU、GPU、FPGA性能对比 |
以FPGA为核心构建了高性能、高密度异构加速卡,基于该加速卡本文分析了解耦电容在PDN设计中的作用并对电路进行了直流和交流后仿真验证.在直流分析中,评估了电源平面直流压降和电流密度;在交流分析中,分析了电路的目标阻抗.最后给出了该加速卡在图像识别中的应用并在功耗和速度上与CPU、GPU进行了对比,对比结果展示了FPGA在计算加速上的优势.
| [1] | Chandana M, Mervin J, David Selvakumar. Power integrity analysis for high performance design[C]//2015 International Conference on Control, Electronics, Renewable Energy and Communications (ICCEREC). Bandung, Indonesia: IEEE Press, 2015: 48-53. |
| [2] |
路宏敏, 郭雁林, 卫晶, 等. 抑制同步开关噪声的新型超宽带电磁带隙结构[J]. 北京邮电大学学报, 2012, 35(4): 15–18.
Lu Hongmin, Guo Yanlin, Wei Jing, et al. New Uultra-wideband electromagnetic bandgap structure used for simultaneous switching noise suppression[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(4): 15–18. doi: 10.3969/j.issn.1007-5321.2012.04.004 |
| [3] | Wang Lixin, Zhang Yuxia, Zhang Gang. Power integrity analysis for high-speed PCB[C]//2010 First International Conference on Pervasive Computing, Signal Processing and Applications. Harbin: IEEE Press, 2010: 414-418. |
| [4] | Drewniak J. Power integrity concepts for high-speed design on multi-layer PCBs[C]//2017 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI). Washington: IEEE Press, 2017: 1-41. |
| [5] | Khened P A, Badiger S D. Power integrity analysis for solid state drive PCB[C]//2016 International Conference on Emerging Technological Trends (ICETT). Kollam, India: IEEE Press, 2016: 1-4. |
| [6] | Yang Zhiping. Fundamentals of power integrity[C]//2017 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI). Washington: IEEE Press, 2017: 1-50. |
| [7] | 张建新.高速PCB的信号和电源完整性问题研究[D].西安: 西安电子科技大学, 2012. |
| [8] | Whatmough Paul N, Shidhartha Das, Zacharias Hadjilambrou, et al. Power integrity analysis of a 28 nm dual-core ARM Cortex-A57 cluster using an all-digital power delivery monitor[J]. IEEE Journal of Solid-State Circuits, 2017, 52(6): 1643–1654. doi: 10.1109/JSSC.2017.2669025 |
| [9] | Bibhu Prasad Nayak, Sreenivasulu Reddy Vedicherla, Dipanjan Gope. Nonorthogonal 2.5-D PEEC for power integrity analysis of package-board geometries[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(4): 1203-1214. |


