2. 北京大学 机器感知与智能教育部重点实验室, 北京 100871
为改善零样本图像分类中相似度度量方法的鲁棒性,引入了一种用于零样本分类的度量学习方法.该方法由自编码构成,能在特征对齐后的语义嵌入空间中学习到最优的度量函数,用于计算测试样本特征和类标签的语义特征的相似度;然后利用近邻思想预测类别标签,进而避免产生不合适距离函数导致的分类错误.实验结果表明,与传统距离度量的算法相比,所提出的方法降低了识别错误率,在公开数据集AWA、CUB和ImNet-2上的分类准确率分别达到94.7%、63.7%和28.59%;同时表明了语义—视觉的映射方向比相反方向的识别准确率高出2.5%~10.1%.
2. MOE Key Laboratory of Machine Perception, Peking University, Beijing 100871, China
To improve the robustness of similarity metric method in zero-shot learning, a new metric learning for zero-shot image classification was introduced. It is composed of autoencoders, which can learn the optimal metric function in the feature-aligned semantic embedding space. The similarity between test sample features and the semantic features of the class labels can be calculated by metric function, predicting the label of the class by the neighboring method. Thus, the classification error caused by inappropriate distance function is prevented. Compared with the traditional distance metric algorithm, the experiments show that the proposed method reduces the recognition error rate; the recognition accuracy is improved to 94.7%, 63.7% and 28.59% on the AWA, CUB and ImNet-2 datasets. At the same time, it was confirmed that the recognition accuracy of the semantic-visual mapping direction was 2.5%~10.1% higher than the opposite direction.
目前基于深度卷积神经网络[1]的图像分类已取得很大进展,但需要大量标注的训练样本.因此,为提高分类模型的泛化性,减少对类标签的依赖,零样本[2]图像识别已经成为计算机视觉领域的研究热点之一.近几年,国内外的学者已经提出许多零样本图像分类的方法.例如,Lampert等[2]提出了基于语义属性的零样本学习;乔雪等[3]引入相对属性的关联性和多任务学习来优化零样本分类模型;程玉虎等[4]考虑到语义属性维度的局限性,将底层特征作为辅助信息.以上方法适用于小数据集,但对大规模数据集进行属性标注是困难的.于是,Socher等[5]将语义向量视为迁移知识,但在学习迁移过程中存在领域漂移[6]的问题,所以Kodirov等[7]提出了基于语义自编码(SAE,semantic autoencoder)的零样本分类模型;Li等[8]提出了一种联合语义空间流行结构和视觉特征空间的最优化模型;Zhang等[9]使用多模融合实现端到端的零样本学习框架.
以上的零样本分类模型多数以语义词向量作为迁移知识,通过增加约束正则项来改善视觉空间到语义空间的映射,提高了分类精度,改善了领域漂移问题.但是,在语义空间中,零样本学习的分类推理阶段很少受到关注,使用固定的度量函数不利于对未知样本的预测.所以,笔者引入度量学习改善零样本分类模型(MLSAZC, metric learning for improving semantic autoencoder zero-shot classification).基本思想是利用图像的视觉特征和类标签的语义词向量,通过度量学习得到度量函数,同时转换原始的数据分布,进一步分离语义空间中的特征分布.
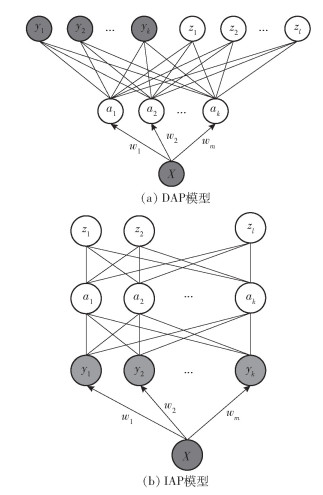
1 基于属性的零样本分类模型在零样本图像分类的任务中,通常以属性作为已知类和未知类的中间层,现有的零样本分类模型主要包括直接属性预测(DAP, direct attribute prediction)和间接属性预测(IAP, indirect attribute prediction)[2],如图 1所示.
|
图 1 基于DAP和IAP的零样本分类模型 |
图 1中,X表示样本的底层特征,a=(a1, a2, …, ak)表示训练类和测试类的共享属性层,Y=(y1, y2, …, yk)和Z=(z1, z2, …, zl)分别表示训练样本(已知类)和测试样本(未知类)的标签.该模型的主要思想是从(X, Y)学习的属性知识a=(a1, a2, …, ak)迁移到未知类别,实现了类别边界的突破.属性层的定义虽然改善了模型的泛化能力,但仍需手工标注.目前大量的工作借助文本的语义信息[10]实现零样本学习,真正意义地不依靠任何样本标签.
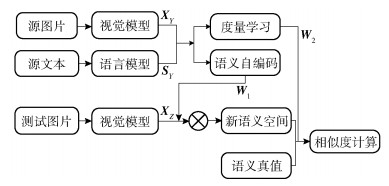
2 度量学习对SAE的零样本分类算法的改进零样本图像分类的总体框架如图 2所示.首先利用深度卷积神经网络[11]训练视觉模型,用于提取视觉特征,其中XY和XZ分别表示已知类别和未知类别的视觉特征;然后采用自然语言模型学习类标签的语义词向量,SY是已知类别的语义特征;再利用SAE学习的映射矩阵W1,将视觉特征映射到语义空间,实现多维数据的特征对齐;最后利用度量学习得到合适的度量函数,计算测试样本特征与语义真值的相似性,进而预测未知样本的标签,W2是由度量学习获得的子空间的投影矩阵.
|
图 2 基于度量学习的零样本图像识别框架 |
自编码是神经网络的一种,可通过增加约束项使模型能够学习到输入数据中有价值的特征.假设XY=(x1, x2, …, xs)∈Rd×s表示训练样本的视觉特征,xi为第i个样本的d维特征,利用映射矩阵W1∈Rk×d将特征向量投影至k维浅层空间,其中k < d,再利用投影逆矩阵W1*∈Rd×k将其投影回原始特征空间,得到X′Y=(x′1, x′2, …, x′s)∈Rd×s.所以为了使重构误差值最小,自编码模型的目标函数可以定义为
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{W}}_1},\mathit{\boldsymbol{W}}_1^ * } \left\| {{\mathit{\boldsymbol{X}}_Y} - \mathit{\boldsymbol{W}}_1^ * {\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{X}}_Y}} \right\|_{\rm{F}}^2 $ | (1) |
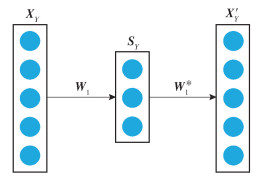
自编码器属于自监督学习,引入的SAE是在其基础上增加额外的监督信息. SAE的结构如图 3所示,使学习到的浅层空间为语义特征表示.用语义特征空间替换浅层空间表示为SY=(s1, s2, …, ss)∈Rk×s,其中si表示表示第i个样本的语义词向量.于是,SAE的目标函数表示为
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{W}}_1},\mathit{\boldsymbol{W}}_1^ * } \left\| {{\mathit{\boldsymbol{X}}_Y} - \mathit{\boldsymbol{W}}_1^ * {\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{X}}_Y}} \right\|_{\rm{F}}^2\;\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{X}}_Y} = {\mathit{\boldsymbol{S}}_Y} $ | (2) |
|
图 3 SAE结构示意图 |
令W1*=W1T,同时避免W1XY=SY的强约束条件,目标函数可化简为
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{W}}_1}} \left\| {{\mathit{\boldsymbol{X}}_Y} - \mathit{\boldsymbol{W}}_1^{\rm{T}}{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{X}}_Y}} \right\|_{\rm{F}}^2 + \lambda \left\| {{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{X}}_Y} - {\mathit{\boldsymbol{S}}_Y}} \right\| $ | (3) |
其中λ为权重系数,且目标函数为凸函数,具有全局最优解.对式(3)求导,并由矩阵的迹性质可得
| $ {\mathit{\boldsymbol{S}}_Y}\mathit{\boldsymbol{S}}_Y^{\rm{T}}{\mathit{\boldsymbol{W}}_1} + \lambda {\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{X}}_Y}\mathit{\boldsymbol{X}}_Y^{\rm{T}} = {\mathit{\boldsymbol{S}}_Y}\mathit{\boldsymbol{X}}_Y^{\rm{T}} + \lambda {\mathit{\boldsymbol{S}}_Y}\mathit{\boldsymbol{X}}_Y^{\rm{T}} $ | (4) |
令A=SYSYT、B=λW1XYXYT和C=(1+λ)×SYXYT,将式(4)化简为Sylvester等式,如式(5)所示.最后用Bartels-Stewar算法解得优化的映射矩阵W1.
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{W}}_1} + {\mathit{\boldsymbol{W}}_1}\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{C}} $ | (5) |
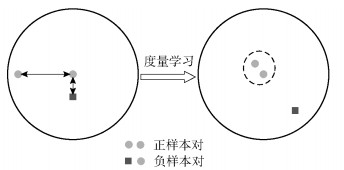
度量学习的根本动机是通过语义-视觉特征对儿学习最优的度量函数,进一步分离语义空间中的特征分布.度量学习的过程如图 4所示.
|
图 4 度量学习示意图 |
目前基于马氏距离函数的度量学习已广泛应用于计算机视觉,与欧氏距离和余弦相似度不同,马氏距离考虑了每个特征之间的关系.一般地,假设数据点p=(p1, p2, …, pk)和q=(q1, q2, …, qk),马氏距离函数表示为
| $ d\left( {\mathit{\boldsymbol{p}},\mathit{\boldsymbol{q}}} \right) = {\left( {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{q}}} \right)^{\rm{T}}}\mathit{\boldsymbol{M}}\left( {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{q}}} \right) $ | (6) |
其中M为半正定矩阵,所以度量学习其实是对M的学习.
针对语义-视觉特征对儿,引入交叉二次判别分析(XQDA, cross-view quadratic discriminant analysis)算法[12],该算法对Bayesian Face[13]和KissMe进行了拓展,主要学习子空间W2=(w1, w2, …, wr)∈Rk×r,同时在r维空间学习距离函数.
假设训练集(S′Y, SY),其中S′Y=(s′1, s′2, …, s′s)是视觉特征在语义空间的特征表示,SY=(s1, s2, …, ss)表示已知类的迁移知识,即类标签在语义空间的语义特征表示.由XQDA算法定义样本特征差Δij=s′i-sj,如果2个样本相同,Δij称为内省差;反之为外省差. Moghaddam等[13]提出2个变量均服从多元高斯分布ΩI和ΩE,且均值为零,与二者对应的协方差矩阵分别表示为ΣI和ΣE.于是,针对符合零均值高斯分布的数据特征,2个样本的距离函数可以表示为
| $ {\rm{Dist}}\left( {\mathit{\boldsymbol{s'}},\mathit{\boldsymbol{s}}} \right) = {\left( {\mathit{\boldsymbol{s'}} - \mathit{\boldsymbol{s}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{W}}_2}\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_I^{ - 1} - \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_E^{ - 1}} \right)\mathit{\boldsymbol{W}}_2^{\rm{T}}\left( {\mathit{\boldsymbol{s'}} - \mathit{\boldsymbol{s}}} \right) $ | (7) |
在上述距离函数中,XQDA算法主要学习核函数M(W2)=W2(ΣI-1-ΣE-1)W2T.对于逆矩阵等式的优化,算法很难求解.参考文献[13]的处理方法,ΩI和ΩE的均值为零,投影后的样本均值仍为零,但产生不同的方差,可用于区分两类.为了求最优矩阵W2,核函数的目标函数可以定义为
| $ J\left( \mathit{\boldsymbol{w}} \right) = \frac{{{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_E}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_I}\mathit{\boldsymbol{w}}}} $ | (8) |
要使J(w)的值最大,将式(8)等价为
| $ \mathop {\max }\limits_\mathit{\boldsymbol{w}} {\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_E}\mathit{\boldsymbol{w}}\;{\rm{s}}.\;{\rm{t}}.\;{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_I}\mathit{\boldsymbol{w}} = 1 $ | (9) |
其中:ΣI-1ΣE的最大特征值即为J(w)的最大值,与最大特征值对应的特征向量即为式(9)的w1解;J(w)的第2大的值对应ΣI-1ΣE的第2大特征向量,以此类推,可以得到式(7)中定义的子空间W2=(w1, w2, …, wr),同时得到该空间的马氏距离函数.
2.3 基于度量学习改进的零样本图像分类定义Y=(y1, y2, …, ys)和Z=(z1, z2, …, zu)分别为已知类s和未知类u的类别标签,且Y∩Z=Ø,SY=(s1, s2, …, ss)∈Rk×s和SY=(s1, s2, …, su)∈Rk×u分别表示已知类和未知类的语义特征.零样本学习的目的是得到一个分类器f:Xz→Z,预测未知类别的标签,Xz={(xi, zi, si)}是测试数据,xi是第i个未知样本的视觉特征,zi和si是未知的.
在测试阶段,通过训练样本得到映射矩阵W1和度量函数Dist(·),分别用2个投影方向预测未知样本的标签.
1) 视觉空间—语义空间
测试样本的视觉特征xi∈Xz经s′i=W1xi嵌入到语义空间,然后利用XQDA算法学习的最优度量函数估计s′i和语义真值的距离,使式(10)取最小值的类标签赋给xi.
| $ \mathit{\Phi }\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \mathop {\arg \min }\limits_{{z_j}} {\rm{Dist}}\left( {{{\mathit{\boldsymbol{s'}}}_i},{\mathit{\boldsymbol{S}}_{zj}}} \right),\;\;\;i,j = 1,2, \cdots ,u $ | (10) |
其中:Szj为第j个未知类的语义真值向量,Dist(·)是由度量学习得到的马氏距离函数.所以,使距离取最小值的zj为测试样本xi的类别标签.
2) 语义空间—视觉空间
利用解码投影矩阵W1T,将测试样本的语义特征si∈SY经x′i=W1Tsi嵌入视觉空间,然后利用相同的度量函数预测未知样本的标签,可表示为
| $ \mathit{\Phi }\left( {{\mathit{\boldsymbol{s}}_i}} \right) = \mathop {\arg \min }\limits_{{z_j}} {\rm{Dist}}\left( {{{\mathit{\boldsymbol{x'}}}_i},{\mathit{\boldsymbol{X}}_{zj}}} \right),\;\;\;i,j = 1,2, \cdots ,u $ | (11) |
其中Xzj为第j个未知类的视觉特征真值.所以,使得距离取最小值的zj为测试样本si的标签.
3 实验仿真及分析 3.1 实验数据集本实验选择动物属性(AWA, animals with attributes)数据集[7]、CUN-200-011 Birds(CUB)数据集[7]和ImageNet-2(ImNet-2)数据集[7],前两者为小型数据集,第3者为大规模数据集,可以充分验证算法的有效性.
AWA数据集有30 475张图片,共50类,其中40类作为已知类,其余10类视为未知类,为满足零样本学习的要求,确保训练集与测试集无交集;CUB数据集分割为150个已知类和50个未知类,共11 788个样本;ImNet-2数据集共有218 000张图片,其中1 000类作为已知类,360类视为未知类.数据集的描述如表 1所示.
|
|
表 1 AWA、CUB和ImNet-2数据集统计 |
在AWA和CUB数据集中,使语义属性作为迁移知识,对每个样本定义85维和312维属性特征;在ImNet-2数据集中,通过word2vec的skip-gram模型,把类标签映射到语义空间,表示为1 000维的语义词向量.由于深度卷积神经网络的泛化能力,在零样本学习中,视觉特征通常利用卷积神经网络提取,本实验采取Googlenet提取的1 024维视觉特征[7].
3.2 实验过程分析本实验验证了MLSAZC模型的分类效果,并与SAE模型做比较.每个数据集分别进行10次分类实验,每次实验随机选择训练样本和测试样本.在训练阶段,采取交叉验证确定SAE模型的最优超参数λ. 图 5给出了零样本分类模型随λ变化的准确率曲线,分别取λ={5, 50, 500, 5 000, 50 000, 500 000}.

|
图 5 分类准确率随超参数λ变化曲线 |
由图 5可以看出,当λ为50万时,模型的识别准确率最高.
在训练阶段,根据训练样本得到SAE模型和距离度量函数;在测试阶段,首先利用SAE模型将测试样本的视觉特征映射到语义空间,再利用度量函数估计输入样本与语义真值的相似度,距离越小说明相似度越大,最终使距离最小的类标签赋给测试样本.
3.3 分类性能比较分析在分类任务中,特征表示会影响分类结果,具有表示的特征会取得更高的识别准确率. SAE模型能够学习到更好的特征表示,再利用度量学习可以进一步改善学习到的特征.于是,利用可视化分析视觉特征在语义空间中的分布情况.
对比图 6(a)和(b)可知,原始视觉特征经过SAE算法映射到语义空间后,相同类别的特征分布变得紧凑.经过度量学习的特征分布如图 6(c)所示,类别间的距离更大,有利于通过距离估计未知样本的类别标签.

|
图 6 语义空间的视觉特征分布可视化 |
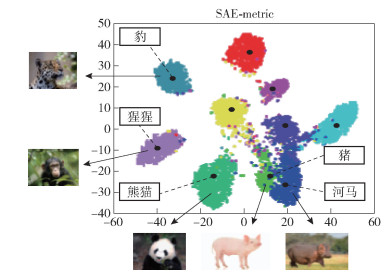
在语义联合嵌入空间中,类标签的语义词向量分布如图 7所示.未知样本的视觉特征紧紧围绕着对应类别的语义词向量,根据二者的距离预测未知样本的类别.由图 7可得出,猪和河马的语义词向量近距离分布,相应视觉特征的分布也相对混淆,有可能对分类结果产生干扰.
|
图 7 视觉特征和语义特征的可视化 |
表 2所示为现有的零样本学习方法在AWA和CUB数据集上的比较.可以看出,度量学习进一步改善了基于SAE的零样本分类算法,在AWA数据集上的准确率可以提高10%左右,在CUB数据集上的准确率也提高了3%左右.由表 3可以看出,在大型ImNet-2数据集中准确率同样提高了5%左右.
|
|
表 2 AWA和CUB数据集的零样本图像分类精度比较 |
|
|
表 3 基于ImNet-2数据集的零样本图像分类精度比较 |
MLSAZC模型中的编码和解码映射函数——MLSAZC(W)和MLSAZC(WT)分别表示视觉—语义特征的映射方向和语义—视觉特征的映射方向.在AWA和CUB数据集上证实了零样本学习中存在的枢纽问题.由表 2得出,与视觉—语义特征的映射方向相比,语义—视觉特征的映射方向的分类准确率要高出3%~10%.
分类的准确率能够反映正确分类的样本数与测试样本总数的关系,不能直观地反映误判的样本数,因此实验中引入混淆矩阵,评估零样本分类模型.以AWA数据集为例,从视觉空间投影到语义空间,SAE模型和MLSAZC模型的混淆矩阵如图 8所示.在混淆矩阵中,类别ID分别为[25, 39, 15, 6, 42, 14, 18, 48, 34, 24],样本被正确分类的准确率通过主对角线上的方框表示,颜色越深表示该类样本正确分类的数量越多.

|
图 8 SAE和MLSAZC分类结果的混淆矩阵 |
从图 8(b)中可以得出,类别42较多地被错分为14号,分别表示猪和河马,这也证实了相近的语义词向量会对相似度的估计产生干扰.
4 结束语针对余弦相似度和欧氏距离等度量方式的局限性,提出了基于度量学习改善SAE的零样本分类算法.首先利用SAE对视觉特征和语义特征构建联合嵌入空间,然后通过度量学习得到距离度量函数.实验结果表明,该方法进一步改善了嵌入空间的特征分布,提高了零样本分类的准确率,缓解了跨领域漂移.目前,零样本分类模型只在小型数据集中取得了明显的改善,但是在大型数据集中,由于把语义词向量作为迁移知识,其提取的方法或结果会直接影响零样本分类模型的效果.因此,下一步将致力于提高大型数据集零样本分类的准确率.
| [1] | Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems. [S. l. ]: Curran Associates Inc, 2012: 1097-1105. |
| [2] | Lampert C H, Nickisch H, Harmeling S. Attribute-based classification for zero-shot visual object categorization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(3): 453–465. doi: 10.1109/TPAMI.2013.140 |
| [3] |
乔雪, 彭晨, 段贺, 等. 基于共享特征相对属性的零样本图像分类[J]. 电子与信息学报, 2017, 39(7): 1563–1570.
Qiao Xue, Peng Chen, Duan He, et al. Zero-shotimage classification based on relative feature of shared features[J]. Journal of Electronics and Information Technology, 2017, 39(7): 1563–1570. |
| [4] |
程玉虎, 乔雪, 王雪松. 基于混合属性的零样本图像分类[J]. 电子学报, 2017, 45(6): 1462–1468.
Cheng Yuhu, Qiao Xue, Wang Xuesong. Zero-shot image classification based on mixed attributes[J]. Chinese Journal of Electronics, 2017, 45(6): 1462–1468. doi: 10.3969/j.issn.0372-2112.2017.06.026 |
| [5] | Socher R, Ganjoo M, Manning C D, et al. Zero-shot learning through cross-modal transfer[C]//Advances in Neural Information Processing Systems. [S. l. ]: Curran Associates Inc, 2013: 935-943. |
| [6] | Fu Y, Hospedales T M, Xiang T, et al. Transductive multi-view zero-shot learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(11): 2332–2345. doi: 10.1109/TPAMI.2015.2408354 |
| [7] | Kodirov E, Xiang T, Gong S. Semantic autoencoder for zero-shot learning[C]//CVPR 2017. Piscataway, NJ: IEEE, 2017: 4447-4456. |
| [8] | Li Y, Wang D, Hu H, et al. Zero-shot recognition using dual visual-semantic mapping paths[C]//IEEE Conference on Computer Vision and Pattern Recognition. [S. l. ]: IEEE Computer Society, 2017: 5207-5215. |
| [9] | Zhang L, Xiang T, Gong S. Learning a deep embedding model for zero-shot learning[EB/OL]. 2016. http://arxiv.org/abs/1611.050B8. |
| [10] | Frome A, Corrado G S, Shlens J, et al. DeViSE: a deep visual-semantic embedding model[C]//International Conference on Neural Information Processing Systems. [S. l. ]: Curran Associates Inc, 2013: 2121-2129. |
| [11] |
李亚, 王广润, 王青. 基于深度卷积神经网络的跨年龄人脸识别[J]. 北京邮电大学学报, 2017, 40(1): 84–88.
Li Ya, Wang Guangrun, Wang Qing. Cross-age face recognition based on deep convolutional neural network[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(1): 84–88. |
| [12] | Liao S, Hu Y, Zhu X, et al. Person reidentification by local maximal occurrence representation and metric learning[EB/OL]. 2014. http://arxiv.org/abs/1406.4216. |
| [13] | Moghaddam B, Jebara T, Pentland A. Bayesian face recognition[J]. Pattern Recognition, 2000, 33(11): 1771–1782. doi: 10.1016/S0031-3203(99)00179-X |
| [14] | Zhang Z, Saligrama V. Zero-shot learning via joint latent similarity embedding[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. San Francisco: CA, 2016: 6034-6042. |
| [15] | Bucher M, Herbin S, Jurie F. Improving semantic embedding consistency by metric learning for zero-shot classiffication[C]//European Conference on Computer Vision. Cham: Springer International Publishing, 2016: 730-736. |
| [16] | Shigeto Y, Suzuki I, Hara K, et al. Ridge regression, hubness, and zero-shot learning[C]//The European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, German: Springer, 2015: 135-151. |
| [17] | Ba J L, Swersky K, Fidler S, et al. Predicting deep zero-shot convolutional neural networks using textual descriptions[C]//IEEE International Conference on Computer Vision. [S. l. ]: IEEE Computer Society, 2015: 4247-4255. |
| [18] | Norouzi M, Mikolov T, Bengio S, et al. Zero-shotlearning by convex combination of semantic embeddings[EB/OL]. 2013. http://arxiv.org/abs/1312.5650. |
| [19] | Fu Z, Xiang T A, Kodirov E, et al. Zero-shot object recognition by semantic manifold distance[C]//Computer Vision and Pattern Recognition. [S. l. ]: IEEE, 2015: 2635-2644. |
| [20] | Fu Y, Sigal L. Semi-supervised vocabulary-informed learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2016: 5337-5346. |


