大规模多输入多输出(MIMO, multiple-input multiple-output)系统通过在收发端部署数以百计的天线获取丰富的分集和复用增益^[1-2].然而大规模天线所需的射频链路带来高昂的硬件成本，业界提出可通过增加模拟移相器以减少射频链路使用.因此，基于混合天线结构的混合预编码技术兼顾硬件成本和运算复杂度，成为大规模MIMO系统的研究热点.

当射频链数不少于用户数时，全阵列天线结构和全数字预编码结构的性能相同^[3]. Ayach等^[4]率先提出一种基于全阵列天线结构的混合预编码策略，先求解出最优一级预编码，通过最小化一级预编码和混合预编码的欧式距离，分别求解出模拟预编码和数字预编码.相同天线结构下，Sohrabi等^[5]利用启发式算法直接求解出混合预编码矩阵. Xu等^[6]也采用类似文献[4]的求解思想，但Xu等^[6]更充分地利用了子阵列天线结构稀疏性，使用的交替优化(AO, alternative optimization)算法复杂度也更低. Liang等^[7]将全阵列天线结构运用到毫米波频段，设计了在模拟和数字域都进行用户间干扰消除的混合预编码.

这些设计都从不同角度降低了传统预编码的算法复杂度和硬件成本，但大多是基于单用户MIMO的场景，没有充分利用大规模MIMO系统的复用增益.因此，笔者综合考虑全阵列天线结构的非凸硬件限制、用户公平性和功率限制，提出一种最小化加权均方误差(WMMSE, weighted minimum mean square error)的三段式混合预编码算法，即先用内点法求解最优一级预编码；再使用AO算法“粗调”迭代求解模拟预编码；最后在“精调”中再次使用内点法改善数字预编码.仿真结果证实所提算法能最大限度减小所求混合预编码矩阵与最优一级预编码矩阵的误差，获得近乎最优的预编码性能增益.

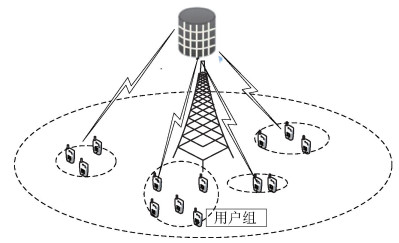
1 下行大规模多用户MIMO系统

全阵列天线结构下的单小区大规模多用户MIMO下行链路如图 1所示，基站端配置有N_t个发射天线，N_rf个射频链(N_rf≪N_t)，每一个射频链通过N_t个移相器和N_t个天线连接^[1]，每个用户有N_r个接收天线.假设一个调度周期内，调度服务用户集记为$\mathscr{K}, \left| {\mathscr{K}} \right| =K$，则用户k的接收信号表示为

$ {\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{s}}_k} + \underbrace {\sum\limits_{k' \ne k,k' \in \mathscr{K}} {\mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_{k'}}{\mathit{\boldsymbol{s}}_{k'}}} }_{用户干扰} + {\mathit{\boldsymbol{n}}_k} $

(1)

其中：H_k为基站端到用户k的下行信道矩阵，且H_k∈${{\mathbb{C}}^{{{N}_{\text{t}}}\times {{N}_{\text{r}}}}}$，s_k∈${{\mathbb{C}}^{{{N}_{\text{s}}}\times 1}}$为其发送信号矢量，n_k∈${{\mathbb{C}}^{{{N}_{\text{r}}}\times 1}}$为噪声信号矢量，A∈${{\mathbb{C}}^{{{N}_{\text{t}}}\times {{N}_{\text{rf}}}}}$为系统的模拟预编码矩阵，B_k∈${{\mathbb{C}}^{{{N}_{\text{rf}}}\times {{N}_{\text{s}}}}}$为用户k的数字预编码矩阵. B=[B₁, B₂, …B_K]∈${{\mathbb{C}}^{{{N}_{\text{rf}}}\times K{{N}_{\text{s}}}}}$为系统的数字预编码矩阵.

假设全阵列天线结构采用N_b位的b(b≥1)比特数字移相器，且移相器幅度常数为μ，则模拟预编码矩阵A的第i行第j列元素取值为^[7]

$ \mathit{\boldsymbol{A}}\left( {i,j} \right) \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }},\mathit{\boldsymbol{ \boldsymbol{\varOmega} = }}\left\{ {\mu {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}n}}{{2{N_{\rm{b}}}}}}}:n = 0,1, \cdots ,{2^{{N_{\rm{b}}}}} - 1} \right\} $

(2)

2 基于WMMSE的混合预编码算法 2.1 问题描述

基于WMMSE的混合预编码算法首先将预编码设计转化为最小化接收信号和发送信号均方误差优化问题，即

$ {e_k} = E\left[ {\left\| {\mathit{\boldsymbol{U}}_k^{\rm{H}}{\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{s}}_k}} \right\|_2^2} \right] $

(3)

其中用户k的均方误差表示为e_k，U_k∈${{\mathbb{C}}^{{{N}_{\text{r}}}\times {{N}_{\text{s}}}}}$是接收端用户k的检测合并器矩阵，接收端采用最小均方误差(MMSE, minimum mean square error)接收机^[7]，设计如下

$ {\mathit{\boldsymbol{U}}_k} = \mathit{\boldsymbol{U}}_k^{{\rm{MMSE}}} = \mathit{\boldsymbol{J}}_k^{ - 1}\mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k} $

(4)

其中${{\mathit{\boldsymbol{J}}}_{k}}\underline{\underline{\Delta }}\sum\limits_{j=1}^{K}{\mathit{\boldsymbol{H}}_{k}^{\text{H}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B}}}_{j}}{{\left(\mathit{\boldsymbol{H}}_{k}^{\text{H}}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B}}}_{j}} \right)}^{\text{H}}}+{{\sigma }^{2}}\mathit{\boldsymbol{I}}}$为协相关矩阵.经过接收端的MMSE接收解调处理后，用户k的均方误差可表示为

$ \begin{array}{*{20}{c}} {{e_k} = E\left[ {\left\| {\mathit{\boldsymbol{U}}_k^{\rm{H}}{\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{s}}_k}} \right\|_2^2} \right] = }\\ {\mathit{\boldsymbol{U}}_k^{\rm{H}}\left( {\sum\limits_{k = 1}^K {\mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}{{\left( {\mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)}^{\rm{H}}} + {\sigma ^2}\mathit{\boldsymbol{I}}} } \right){\mathit{\boldsymbol{U}}_k} - }\\ {2{\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{U}}_k^{\rm{H}}\mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right\} + 1} \end{array} $

(5)

对于用户k，不同用户的均方误差应尽量保持一致，以保证用户公平性.因此，以WMMSE为优化目标得到式(6)，其中ρ_k为第k个用户均方误差的权重.

$ \mathop {{\rm{minimize}}}\limits_{\left\{ {\mathit{\boldsymbol{A}},{\mathit{\boldsymbol{B}}_k},{\mathit{\boldsymbol{U}}_k}} \right\}} \sum\limits_{k = 1}^K {{\rho _k}{e_k}} $

(6)

考虑移相器的硬件限制和单用户发射功率受限，设计如下基于WMMSE的混合预编码优化问题：

$ \begin{array}{*{20}{c}} {\mathop {{\rm{minimize}}}\limits_{\left\{ {\mathit{\boldsymbol{A}},{\mathit{\boldsymbol{B}}_k},{\mathit{\boldsymbol{U}}_k}} \right\}} \sum\limits_{k = 1}^K {{\rho _k}{e_k}} }\\ {{\rm{subject}}\;{\rm{to}}\;{\rm{Tr}}\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)}^{\rm{H}}}} \right) \le \frac{{{P_{{\rm{sum}}}}}}{K},\;\;\forall k\left( {{\rm{c1}}} \right)}\\ {\mathit{\boldsymbol{A}}\left( {i,j} \right) \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\left( {{\rm{c2}}} \right)} \end{array} $

(7)

其中：P_sum为基站总发射功率，K为总用户数.由于式(7)中A矩阵的元素值离散，B矩阵元素值连续，且该优化问题非凸，很难采用常规凸优化思路求解.因此，在求解最优的一级预编码矩阵F_opt时先不考虑式(7)中(c2)的移相器硬件约束.

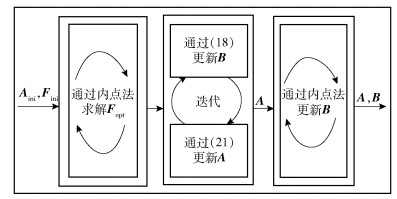
2.2 算法步骤

设计一种基于WMMSE的三段式混合预编码算法求解式(7)，其算法逻辑见图 2，包括内点法求解最优一级预编码；“粗调”求解模拟和数字预编码以逼近最优一级预编码的性能；“精调”求解数字预编码矩阵3部分.

2.2.1 内点法求解最优一级预编码矩阵F_opt

所提算法需先求出最优一级预编码矩阵F_opt，再通过AB逼近最优一级预编码矩阵F_opt.令${{\mathit{\boldsymbol{F}}}_{k}}\underline{\underline{\Delta }}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B}}}_{k}}, {{\mathit{\boldsymbol{F}}}_{\text{opt}}}=\left[{{\mathit{\boldsymbol{F}}}_{1}}, {{\mathit{\boldsymbol{F}}}_{2}}, \cdots, {{\mathit{\boldsymbol{F}}}_{K}} \right]\in {{\mathbb{C}}^{{{N}_{\text{t}}}\times K{{N}_{s}}}}$，式(7)可转化为

$ \begin{array}{*{20}{c}} {\mathop {{\rm{minimize}}}\limits_{\left\{ {{\mathit{\boldsymbol{F}}_k}} \right\}} \sum\limits_{k = 1}^K {{\rho _k}{e_k}} }\\ {{\rm{subject}}\;{\rm{to}}\;{\rm{Tr}}\left( {{\mathit{\boldsymbol{F}}_k}\mathit{\boldsymbol{F}}_k^{\rm{H}}} \right) \le \frac{{{P_{{\rm{sum}}}}}}{K},k = 1, \cdots ,K} \end{array} $

(8)

结合式(4)，当${{\mathit{\boldsymbol{F}}}_{k}}\underline{\underline{\Delta }}\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B}}}_{k}}$，最优接收机可表示为

$ \mathit{\boldsymbol{U}}_k^{{\rm{MMSE}}} = {\left( {\sum\limits_{j = 1}^K {\mathit{\boldsymbol{H}}_k^{\rm{H}}\mathit{\boldsymbol{F}}_j^{\rm{H}}{\mathit{\boldsymbol{F}}_j}{\mathit{\boldsymbol{H}}_k}} + {\sigma ^2}\mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_j},\forall k $

(9)

同理，最小均方误差e_k可以表示为

$ \begin{array}{*{20}{c}} {{e_k} = \mathit{\boldsymbol{U}}_k^{\rm{H}}\left( {\sum\limits_{k = 1}^K {\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_k}{{\left( {\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_k}} \right)}^{\rm{H}}}} + {\sigma ^2}\mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{U}}_k} - }\\ {2{\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{U}}_k^{\rm{H}}\mathit{\boldsymbol{H}}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_k}} \right\} + 1} \end{array} $

(10)

由于式(8)是凸问题，可采用内点法^[6]求解F_opt，下文给出了内点法求解F_opt的收敛性仿真验证.

2.2.2 AO“粗调”模拟预编码矩阵

求解出F_opt后，混合预编码矩阵求解问题转化为最小化F_opt和AB元素误差和的问题.为简化表达，令F=F_opt表示求出的最优一级预编码矩阵，转化为如下优化问题

$ \begin{array}{*{20}{c}} {{{\rm{minimize}}}\;{\rm{Tr}}\left\{ {{{\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{AB}}} \right)}^{\rm{H}}}\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{AB}}} \right)} \right\}}\\ {{\rm{subject}}\;{\rm{to}}\;{\rm{Tr}}\left( {{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)}^{\rm{H}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right) \le \frac{{{P_{{\rm{sum}}}}}}{K},\;\;\forall k\left( {{\rm{c1}}} \right)} \end{array} $

(11)

其中F-AB可写为

$ \mathit{\boldsymbol{F}} - \mathit{\boldsymbol{AB}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_1}}\\ {{\mathit{\boldsymbol{F}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{F}}_{K{N_{\rm{s}}}}}} \end{array}} \right]^{\rm{T}}} - \mathit{\boldsymbol{A}}{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{K{N_{\rm{s}}}}}} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_1} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{F}}_2} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{F}}_K} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_{K{N_{\rm{s}}}}}} \end{array}} \right]^{\rm{T}}} $

(12)

则式(11)可转化为

$ \begin{array}{*{20}{c}} {\mathop {{\rm{minimize}}}\limits_{\left\{ {{\mathit{\boldsymbol{B}}_k}} \right\}} \sum\limits_{k = 1}^K {{\rm{Tr}}\left\{ {{{\left( {{\mathit{\boldsymbol{F}}_k} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)}^{\rm{H}}}\left( {{\mathit{\boldsymbol{F}}_k} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)} \right\}} }\\ {{\rm{subject}}\;{\rm{to}}\;{\rm{Tr}}\left( {{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)}^{\rm{H}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right) \le \frac{{{P_{{\rm{sum}}}}}}{K},\;\;\forall k\left( {{\rm{c1}}} \right)} \end{array} $

(13)

利用AO算法“粗调”求解A和B，其过程如下：

1) 初始化A，即A中每个元素设为μe^jθ，其中θ为任意相角；

2) 给定A，通过式(16)求B，则式(13)是标准二次凸优化问题，可用拉格朗日乘数法求B.拉格朗日方程L(B, λ_k)如式(14)所示，其中λ_k为用户k的拉格朗日系数.

$ \begin{array}{l} L\left( {\mathit{\boldsymbol{B}},{\lambda _k}} \right) \buildrel \Delta \over = \sum\limits_{k = 1}^K {{\rm{Tr}}\left( {\mathit{\boldsymbol{F}}_k^{\rm{H}}{\mathit{\boldsymbol{F}}_k} - \mathit{\boldsymbol{F}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k} - \mathit{\boldsymbol{B}}_k^{\rm{H}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{F}}_k} - } \right.} \\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{B}}_k^{\rm{H}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right) - {\lambda _k}{\rm{Tr}}\left( {\mathit{\boldsymbol{B}}_k^{\rm{H}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k} - \frac{{{P_{{\rm{sum}}}}}}{\mathit{\boldsymbol{K}}}} \right) \end{array} $

(14)

L(B, λ_k)对B_k求一阶偏导数可得

$ \frac{{\partial L\left( {\mathit{\boldsymbol{B}},{\lambda _k}} \right)}}{{\partial {\mathit{\boldsymbol{B}}_k}}} = 2\left( {1 + {\lambda _k}} \right){\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k} - 2\mathit{\boldsymbol{F}}_k^{\rm{H}}\mathit{\boldsymbol{A}} $

(15)

令$\frac{{\partial L\left({{\mathit{\boldsymbol{B}}_k}, {\mathit{\boldsymbol{\lambda }}_k}} \right)}}{{\partial {\mathit{\boldsymbol{B}}_k}}} = 0$，可得一阶最优条件是

$ {\mathit{\boldsymbol{B}}_k} = \frac{1}{{1 + {\lambda _k}}}{\left( {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}\mathit{\boldsymbol{F}}_k^{\rm{H}}\mathit{\boldsymbol{A}} $

(16)

结合KKT条件，先令$\frac{{\partial L\left({{\mathit{\boldsymbol{B}}_k}, {\mathit{\boldsymbol{\lambda }}_k}} \right)}}{{\partial {\mathit{\boldsymbol{\lambda }}_k}}} = 0$，再将式(16)代入$\frac{{\partial L\left({{\mathit{\boldsymbol{B}}_k}, {\mathit{\boldsymbol{\lambda }}_k}} \right)}}{{\partial {\mathit{\boldsymbol{\lambda }}_k}}} = 0$可得^[6]

$ {\lambda _k} = {\left( {\sqrt {\frac{{{\rm{Tr}}\left\{ {\mathit{\boldsymbol{F}}_k^{\rm{H}}\mathit{\boldsymbol{A}}{{\left( {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}} \right)}^{ - 1}}\mathit{\boldsymbol{AF}}_k^{\rm{H}}} \right\}}}{{{P_{{\rm{sum}}}}/K}}} - 1} \right)^ + } $

(17)

其中(a)⁺$\underline{\underline \Delta } $max{0, a}.

3) 给定B，求解最优模拟预编码矩阵A.假设F矩阵的第k行行矢量为F⁽ⁱ⁾∈${{\mathbb{C}}^{1+K{{N}_{s}}}}$，A矩阵的第k行行矢量为A⁽ⁱ⁾∈${{\mathbb{C}}^{1+{{N}_{\text{rf}}}}}$，则F－AB为

$ \mathit{\boldsymbol{F}} - \mathit{\boldsymbol{AB}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}^{\left( 1 \right)}}}\\ {{\mathit{\boldsymbol{F}}^{\left( 2 \right)}}}\\ \vdots \\ {{\mathit{\boldsymbol{F}}^{\left( {{N_{\rm{t}}}} \right)}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\left( 1 \right)}}\mathit{\boldsymbol{B}}}\\ {{\mathit{\boldsymbol{A}}^{\left( 2 \right)}}\mathit{\boldsymbol{B}}}\\ \vdots \\ {{\mathit{\boldsymbol{A}}^{\left( {{N_{\rm{t}}}} \right)}}\mathit{\boldsymbol{B}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}^{\left( 1 \right)}} - {\mathit{\boldsymbol{A}}^{\left( 1 \right)}}\mathit{\boldsymbol{B}}}\\ {{\mathit{\boldsymbol{F}}^{\left( 2 \right)}} - {\mathit{\boldsymbol{A}}^{\left( 2 \right)}}\mathit{\boldsymbol{B}}}\\ \vdots \\ {{\mathit{\boldsymbol{F}}^{\left( {{N_{\rm{t}}}} \right)}} - {\mathit{\boldsymbol{A}}^{\left( {{N_{\rm{t}}}} \right)}}\mathit{\boldsymbol{B}}} \end{array}} \right] $

(18)

根据式(18)，式(11)可转化为

$ \begin{array}{*{20}{c}} {{\rm{Tr}}\left\{ {{{\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{AB}}} \right)}^{\rm{H}}}\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{AB}}} \right)} \right\} = }\\ {{\rm{Tr}}\left\{ {{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}^{\left( 1 \right)}} - {\mathit{\boldsymbol{A}}^{\left( 1 \right)}}\mathit{\boldsymbol{B}}}\\ {{\mathit{\boldsymbol{F}}^{\left( 2 \right)}} - {\mathit{\boldsymbol{A}}^{\left( 2 \right)}}\mathit{\boldsymbol{B}}}\\ \vdots \\ {{\mathit{\boldsymbol{F}}^{\left( {{N_{\rm{t}}}} \right)}} - {\mathit{\boldsymbol{A}}^{\left( {{N_{\rm{t}}}} \right)}}\mathit{\boldsymbol{B}}} \end{array}} \right]}^{\rm{H}}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}^{\left( 1 \right)}} - {\mathit{\boldsymbol{A}}^{\left( 1 \right)}}\mathit{\boldsymbol{B}}}\\ {{\mathit{\boldsymbol{F}}^{\left( 2 \right)}} - {\mathit{\boldsymbol{A}}^{\left( 2 \right)}}\mathit{\boldsymbol{B}}}\\ \vdots \\ {{\mathit{\boldsymbol{F}}^{\left( {{N_{\rm{t}}}} \right)}} - {\mathit{\boldsymbol{A}}^{\left( {{N_{\rm{t}}}} \right)}}\mathit{\boldsymbol{B}}} \end{array}} \right]} \right\} = }\\ {\sum\limits_{n = 1}^{{N_{\rm{t}}}} {{\rm{Tr}}\left\{ {{{\left( {{\mathit{\boldsymbol{F}}^{\left( n \right)}} - {\mathit{\boldsymbol{A}}^{\left( n \right)}}\mathit{\boldsymbol{B}}} \right)}^{\rm{H}}}\left( {{\mathit{\boldsymbol{F}}^{\left( n \right)}} - {\mathit{\boldsymbol{A}}^{\left( n \right)}}\mathit{\boldsymbol{B}}} \right)} \right\}} } \end{array} $

(19)

拆分后的每一项Tr{(F⁽ⁿ⁾－A⁽ⁿ⁾B)^H(F⁽ⁿ⁾－A⁽ⁿ⁾B)}相互独立.为了使整个求和式最小，式(19)可转化为每一项求和最小.式(19)可转化为N_t个形如式(20)的优化目标

$ \mathop {{\rm{minimize}}}\limits_{\left\{ {{\mathit{\boldsymbol{A}}^{(n)}}} \right\}} \;{\rm{Tr}}\left\{ {{{\left( {{\mathit{\boldsymbol{F}}^{\left( n \right)}} - {\mathit{\boldsymbol{A}}^{\left( n \right)}}\mathit{\boldsymbol{B}}} \right)}^{\rm{H}}}\left( {{\mathit{\boldsymbol{F}}^{\left( n \right)}} - {\mathit{\boldsymbol{A}}^{\left( n \right)}}\mathit{\boldsymbol{B}}} \right)} \right\} $

(20)

式(20)是典型的二阶锥规划(SOCP, second order cone program)问题^[6].此时，再考虑移相器硬件约束(c2)，根据式(21)将A矩阵的每个元素A(i, j)“投影”到移相器离散取值集合Ω中，确定最优的相位取值$\widehat{n}$，得到元素值离散的A矩阵.

$ \hat n = \mathop {\arg \min }\limits_{n \in \left\{ {0,1, \cdots ,{2^N}b - 1} \right\}} \left| {\mathit{\boldsymbol{A}}\left( {i,j} \right) - \mu {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}n}}{{{2^N}b}}}}} \right| $

(21)

AO算法通过迭代步骤2)和3)，直至收敛，达到给定精度，可“粗调”求出较为理想的A.

2.2.3 内点法“精调”求解最优数字预编码矩阵B

求出A后，将其代回式(8)，再次采用内点法，“精调”求解最优数字预编码矩阵B.由于B的维度远低于F，通过“精调”，可在不明显增加复杂度的情况下，大大弥补AO“粗调”的误差，进一步提升混合预编码性能增益.

同内点法求解F过程类似，给定ρ_k和U_k时，求B等效于如下二次约束的二次规划问题(QCQP, quadratically constrained quadratic program)问题^[8].

$ \begin{array}{*{20}{c}} {\mathop {{\rm{minimize}}}\limits_{\left\{ {{\mathit{\boldsymbol{B}}_k}} \right\}} \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{B}}_k}{\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {\sum\limits_{j = 1}^K {{\rho _j}\mathit{\boldsymbol{H}}_j^{\rm{H}}{\mathit{\boldsymbol{U}}_j}\mathit{\boldsymbol{U}}_j^{\rm{H}}{\mathit{\boldsymbol{H}}_j}} } \right)\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} - }\\ {2\sum\limits_{k = 1}^K {{\mathop{\rm Re}\nolimits} \left\{ {{\rho _k}{\mathit{\boldsymbol{U}}_k}{\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right\}} }\\ {{\rm{subject}}\;{\rm{to}}\;{\rm{Tr}}\left\{ {{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right)}^{\rm{H}}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}_k}} \right\} \le \frac{{{P_{{\rm{sum}}}}}}{K},\forall k} \end{array} $

(22)

3 仿真分析

考虑单小区大规模多用户MIMO场景，采用合适的分组策略对小区中的用户进行分组.仿真中，小区内共6个用户分簇，簇内均匀分布4个用户，基站每次选择其中一个用户分簇进行调度服务.信道模型采用空间信道模型^[1] (SCM, spatial channel model)，仿真参数如表 1所示.

3.1 算法收敛性分析

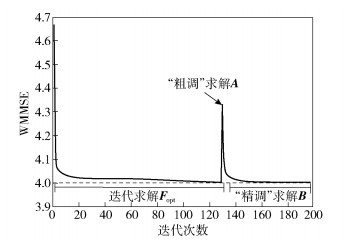
图 3给出μ=e^－5，N_t=64，Δ_F=5e^－5，Δ_B=5e^－6时，WMMSE随着迭代次数增加的变化趋势.其中Δ_F和Δ_B分别为求解F_opt和B的精度值.整个算法WMMSE的变化趋势也可分为3段.第1段中算法通过内点法求解F_opt，可看出WMMSE迅速下降，经过20次迭代后下降速度逐渐变缓，约130次迭代后，WMMSE几乎不再变化，算法达到给定收敛精度.第2段中通过AO算法“粗调”求解F_opt，WMMSE有明显跳跃，说明AO算法不能完全逼近F_opt，且存在一定差距，而此差距很难继续通过A的优化来减小.所以，继续采用内点法对B“精调”.第3段是给定A时，通过内点法继续对B优化.收敛速度由快至慢，最终收敛到给定精度Δ_B.但“精调”迭代次数(约70次)明显小于求F_opt的迭代次数，可见“精调”算法复杂度远小于求F_opt的算法复杂度.

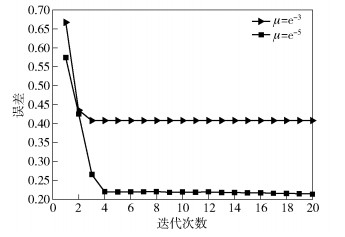
为证明AO算法收敛性，计算不同参数下，随着迭代次数增加，F_opt和AB间的误差，即ξ=‖F_opt－AB‖₂. 图 4给出随AO迭代次数增加，移相器幅度为μ=e^－3和μ=e^－5时的ξ，可看出AO算法会先迅速收敛至给定误差值，随着迭代次数增加，收敛速度缓慢下降.由于模拟移相器解空间有限，AO算法只会收敛到给定值而非0.随着迭代增加，A可行解的限制变大，ξ很难进一步被缩小.此外，当μ越小时，ξ越小，说明μ对混合预编码性能有重要影响.在功率限制下，μ越小，B的可调范围越大，而B的调节精度明显高于A，对系统性能的提升也更明显.

3.2 预编码性能分析

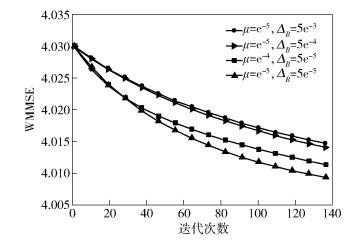
从WMMSE、用户加权速率和(WSR，weighted sum rate)以及累积概率分布分析所提算法性能. 图 5给出了所提算法的WMMSE，可看出，当μ和Δ_B精度越高，所提算法的WMMSE越小.此外，天线功率受限时，μ过大会使模拟预编码对性能的影响大于数字预编码.但模拟预编码硬件结构的非凸性，使其对系统性能增益较小.所以合理设计μ对混合预编码的性能也有非常重要的影响.

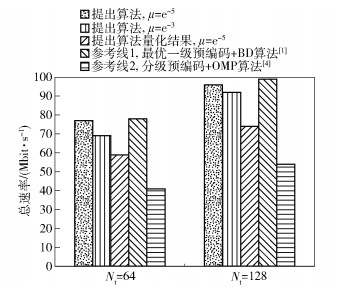
图 6给出了不同天线数下，一个调度周期内的WSR.对比了最优一级块对角(BD, block diagonalization)数字预编码^[1]和基于正交匹配追踪(OMP, orthogonal matching pursuit)的混合预编码算法^[4].所提算法相比于最优一级BD数字预编码具有更低的成本和更高的能量效率. OMP算法需要从候选矢量集合中选择与残差矩阵相关性最大的模拟预编码矢量，相对于所提算法计算复杂度较高. Ayach等^[4]考虑单用户MIMO场景，而所提算法考虑多用户MIMO场景和移相器实际硬件约束，充分利用复用增益且接近最优一级预编码.从图 6看出，μ越小，整体预编码性能越好.此外，仿真中还给出了A经过相位量化后最终获得的用户速率.实际量化采用8位数字移相器.量化后用户总速率的损失可通过提高移相器相位精度弥补.

图 7给出了当N_t分别为32、64和128时所提算法的累积分布函数.可见，当天线数越多时，用户的可达瞬时速率显著提高.

3.3 算法复杂度分析

所提算法中第1步和第3步采用内点法求解优化问题，其计算复杂度与求解矩阵元素个数相关.假设经过T_F次迭代后F_opt达到指定精度，其需要调节的权重因子有KN_t，则求解F_opt的总算法复杂度为O((KN_t)^3.5T_F).求解B需要更新的变量数为KN_rf，则“精调”算法复杂度为O((KN_rf)^3.5T_B)，其中T_B为“精调”迭代次数.

AO算法中，给定A时，B存在闭式解，其计算复杂度为O(K).给定B，求A可转化为求解N_t个SOCP问题，其中每个SOCP需要求N_rf个复数变量，故求B的算法复杂度为O((N_rf)^3.5N_t).假设“粗调”所需迭代次数为T_A，则AO算法复杂度为O((N_rf)^3.5N_tT_A).综上所述，每次调度过程的计算复杂度为

$ O\left( {{{\left( {K{N_{\rm{t}}}} \right)}^{3.5}}{T_F}} \right) + O\left( {{{\left( {{N_{{\rm{rf}}}}} \right)}^{3.5}}{N_{\rm{t}}}{T_A}} \right) + O\left( {{{\left( {K{N_{{\rm{rf}}}}} \right)}^{3.5}}{T_B}} \right) $

4 结束语

全阵列天线结构的性能良好且硬件复杂度低.目前全阵列结构下大规模MIMO系统主要基于单用户MIMO场景.笔者提出一种基于多用户WMMSE的三段式混合预编码算法，利用全阵列天线结构且充分利用复用增益.对算法的收敛性，复杂度及性能都进行了分析和验证，且对移相器的结构提出了一定的改进建议.