2. 北京智芯微电子科技有限公司, 北京 102200;
3. 中国电力科学研究院, 北京 100192
提出了一种基于熵和线性关系的两级流量异常检测方法,综合考虑了流量异常检测方法的准确性和实时性要求.该方法在时间域上设定两级动态阈值,采用基于熵的方法对异常时间点进行检测,对熵值变化程度明显的时间点可使用一级阈值检测出来,而对熵值变化程度处于一级阈值和二级阈值之间的时间点采用基于线性关系的方法再次进行检测,并通过定义的报警触发函数识别异常类型.仿真实验结果证明,该方法在准确性和实时性方面优于现有的方法.
2. Beijing Smartchip Microelectronics Technology Company Limited, Beijing 102200, China;
3. China Electric Power Research Institute, Beijing 100192, China
To improve the accuracy and real-time traffic anomaly detection methods, a two-stage traffic anomaly detection method based on entropy and linear relation was presented. A two-level dynamic threshold was set and used based on entropy and linear relation to detect abnormal traffic in time domain. The type of traffic anomaly can be indentified through the alarm trigger function. Simulations verify that this method is superior to the existing methods in the accuracy and real-time respects.
流量异常检测的研究思想主要分为2种[1]:基于数据挖掘的思想和基于时域分析的思想.基于第2种思想的方法简便快速,已有了许多成果. Wang等[2]提出了一种基于线性回归的流量异常检测方法,提高了检测的准确率. Callegari等[3]采用累加和算法检测网络流量特征的显著变化. Nychis等[4]利用地址与端口的分布关系检测异常事件. Callegari等[5]在信息熵的基础上利用Jenson-Shannon散度作为检测指标来发现网络中的异常点. Navaz等[6]和Huo等[7]在几种常见异常类型发生时对信息熵的变化情况进行了研究.
现有流量异常检测方法大多忽略了异常类型的识别和实时性的要求,而且当异常流量远小于背景流量时,传统的基于熵的方法的准确率明显下降[8].笔者提出了一种基于熵和线性关系的两级流量异常检测方法,综合考虑了准确率和实时性要求,并且能够识别异常类型.
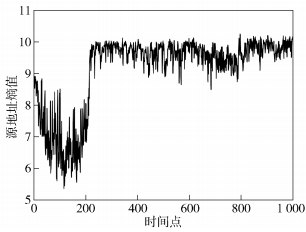
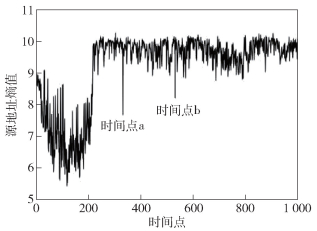
1 基于熵的流量模型正常情况下,一定时间窗口内源地址、源端口、目的地址、目的端口的熵值序列维持在较为稳定的水平[4, 9],如图 1所示(以源地址熵值序列为例).异常发生时,4种属性的熵值会随之变化,出现突变点,如图 2所示. 图 2中,时间点a、b因存在异常流量,源地址熵值的变化较为明显.
|
图 1 无异常流量源地址熵值序列 |
|
图 2 有异常流量源地址熵值序列 |
传统的基于熵值的流量异常检测方法通过判断时间点t上的熵值变化是否超过预先设定的阈值来确定时间点t是否发生了异常,此方法的瓶颈在于合理阈值的设定.由于某些异常流量数量远小于背景流量数量,单一属性的熵值变化程度并非特别明显,无法将此异常时间点从正常时间点中分离出来.如果阈值设定得过高,检测率较低,而设定过低又导致误检率较高.李中魁[10]针对这一不足对阈值设定进行了改进,但计算较为复杂.
为提高异常流量检测的准确率,笔者提出了基于熵的异常检测方法和基于线性关系的异常检测方法.在基于熵的异常检测方法中通过设定两级动态阈值来提高检测的准确率.当熵值变化程度超过了一级阈值时,可判断网络中出现了异常;当熵值变化程度处于一级阈值和二级阈值之间时,为了减小异常检测的误检率,不能立即判断异常的出现,需进一步通过基于线性关系的方法来检测源端口熵值与目的端口熵值、源地址熵值与目的地址熵值是否偏离了该有的线性关系来判断异常的发生.此外,由于建立熵值间的动态线性关系会消耗一定的时间成本,为降低时延,仅在熵值变化程度处于一级阈值和二级阈值时对熵值间的线性关系进行建模.
2 基于熵的流量异常检测方法由于在流量的粗粒度层次即整个报文流上进行异常检测时时延较小[11],所以在流量的粗粒度层对熵值进行计算.
2.1 信息熵假设在时间点t上存在流量聚合流St,聚合流中源地址、源端口、目的地址、目的端口的熵值分别表示为Hsa, t、Hsp, t、Hda, t、Hdp, t,那么聚合流St上的熵值四元组定义为Ht=[Hsa, t, Hsp, t, Hda, t, Hdp, t].聚合流St中源地址的熵值计算公式为
| $ {H_{sa,t}} = - \sum\limits_{i = 1}^n {{P_i}\ln {P_i}} $ | (1) |
其中:n为聚合流中流量总数,Pi为相应源地址出现的概率.源端口、目的地址、目的端口的熵值同理可得.
2.2 两级动态阈值通过对一天中正常历史流量的属性熵值统计分析发现,源地址、源端口、目的地址、目的端口熵值序列呈现趋势性变化.以源地址熵值序列为例,如图 1所示,从时间点0开始大约至时间点150熵值减小,时间点150大约至时间点250熵值增大,时间点250之后熵值的变化较为平稳.为了消除熵值的趋势性变化,方便计算熵值变化程度,对熵值序列进行一阶差分处理,处理后的序列表示为H′t:
| $ {{\mathit{\boldsymbol{H'}}}_t} = {\mathit{\boldsymbol{H}}_t} - {\mathit{\boldsymbol{H}}_{t - 1}} $ | (2) |
当网络中不存在异常时,一定时间窗口内的一阶差分熵值维持在一定的范围内,但由于每天的不同时段一阶差分熵值存在一定差异,使用静态阈值不能准确判断熵值变化程度是否存在异常,因此动态地设定阈值可提高检测率.
假设时间窗口大小为N,时间尺度大小为T,当前检测的时间点为t,假设时间点t之前的N个聚合流内不存在异常流量,根据该N个聚合流的一阶差分熵值序列动态设定时间点t的两级阈值.
定义1 熵值变化程度.定义时间点t上的熵值变化程度为:时间点t上的一阶差分熵值H′t与时间窗口内的N个一阶差分熵值的平均值E′t之差.熵值变化程度四元组表示为
| $ \begin{array}{*{20}{c}} {\Delta {{\mathit{\boldsymbol{H'}}}_t} = {{\mathit{\boldsymbol{H'}}}_t} - {{\mathit{\boldsymbol{E'}}}_t} = }\\ {\left[ {{{H'}_{sa,t}},{{H'}_{sp,t}},{{H'}_{da,t}},{{H'}_{dp,t}}} \right] - \left[ {{{E'}_{sa,t}},{{E'}_{sp,t}},{{E'}_{da,t}},{{E'}_{dp,t}}} \right] = }\\ {\left[ {\Delta {{H'}_{sa,t}},\Delta {{H'}_{sp,t}},\Delta {{H'}_{da,t}},\Delta {{H'}_{dp,t}}} \right]} \end{array} $ | (3) |
定义2 两级动态阈值.通过对大量历史流量的源地址、目的地址、源端口和目的端口的一阶差分熵值统计发现,这4种属性的一阶差分熵值的分布近似符合正态分布的特征.一阶差分熵值在(E′t-3δ′t, E′t+3δ′t)范围内的概率约是99.74%,在(E′t-2δ′t, E′t+2δ′t)范围内的概率约是95.45%.因此,将一级阈值设定为3倍标准差,二级阈值设定为2倍标准差.两级动态阈值的设定如下:
| $ {{\mathit{\boldsymbol{E'}}}_t} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\mathit{\boldsymbol{H'}}}_i}} $ | (4) |
| $ \mathit{\boldsymbol{\delta '}}_t^2 = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\mathit{\boldsymbol{H'}}}_i} - {{\mathit{\boldsymbol{E'}}}_t}} \right)}^2}} $ | (5) |
其中E′t和δ′t2分别为时间窗口内的一阶差分熵值四元组的平均值和方差.时间点t上的两级动态阈值λt=(λt1, λt2),其中λt1=±3δ′t,λt2=±2δ′t.
2.3 报警触发函数定义3 报警触发函数.以源地址熵值为例,定义报警触发函数alarm(Hsa, t):
| $ {\rm{alarm}}\left( {{H_{sa,t}}} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 2,\\ 1,\\ 0,\\ - 1,\\ - 2, \end{array}&\begin{array}{l} \Delta {{H'}_{sa,t}} > 3{{\delta '}_{sa,t}}\\ 2{{\delta '}_{sa,t}} < \Delta {{H'}_{sa,t}} \le 3{{\delta '}_{sa,t}}\\ - 2{{\delta '}_{sa,t}} \le \Delta {{H'}_{sa,t}} \le 3{{\delta '}_{sa,t}}\\ - 3{{\delta '}_{sa,t}} \le \Delta {{H'}_{sa,t}} \le - 2{{\delta '}_{sa,t}}\\ \Delta {{H'}_{sa,t}} < - 3{{\delta '}_{sa,t}} \end{array} \end{array}} \right. $ | (6) |
其中δ′sa, t为δ′t的源地址分量. alarm(Hsa, t)=±2表明源地址熵值变化程度超出了一级阈值的范围;alarm(Hsa, t)=±1表明源地址熵值变化程度介于一级阈值与二级阈值之间;alarm(Hsa, t)=0表明源地址熵值没有明显的变化.其他属性的报警触发函数同理可得,那么时间点t上的报警触发四元组定义为
| $ \begin{array}{*{20}{c}} {{\rm{alarm}}\left( {{\mathit{\boldsymbol{H}}_t}} \right) = }\\ {\left[ {{\rm{alarm}}\left( {{H_{sa,t}}} \right),{\rm{alarm}}\left( {{H_{sp,t}}} \right),{\rm{alarm}}\left( {{H_{da,t}}} \right){\rm{alarm}}\left( {{H_{dp,t}}} \right)} \right]} \end{array} $ |
若alarm(Ht)中的所有分量值都等于0,说明时间点t上没有异常发生,网络是安全的;若任意一个或多个分量值等于±2,可判断时间点t上发生了异常;若没有分量值为±2,且任意一个或多个分量值等于±1.为了降低误检率,不能立即判断时间点t上发生了异常,还需根据多个属性的熵值间是否偏离了该有的线性关系来判断异常是否发生.
2.4 异常类型判定网络出现异常后,地址和端口号的熵值相应的增大或减小[7],不同异常类型出现时,各属性的熵值变化情况如表 1所示.
|
|
表 1 不同异常类型的熵值变化情况 |
当时间点t出现异常时,根据报警触发函数alarm(Ht)各分量的正负号识别异常类型,符号为正表示熵值增大,为负表示熵值减小.例如,当alarm(Hsa, t)>0且alarm(Hsp, t)=0、alarm(Hda, t) < 0、alarm(Hdp, t) < 0时,可判断时间点t上出现了DDoS攻击.
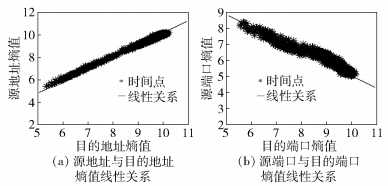
3 基于线性关系的流量异常检测方法 3.1 熵值间线性回归分析对正常情况下大量历史流量的源地址熵值和目的地址熵值、源端口熵值和目的端口熵值分别进行了一元线性回归的建模,发现源地址熵值随目的地址熵值的增大而增大,可拟合为一条斜率为正的直线,具有正线性关系,如图 3(a)所示;源端口熵值随目的端口熵值的增大而减小,可拟合为一条斜率为负的直线,具有负线性关系,如图 3(b)所示.
|
图 3 熵值间的线性关系 |
以源地址熵值和目的地址熵值为例,其线性关系表达式为
| $ {H_{sa,t}} = \alpha {H_{da,t}} + \beta + \varepsilon $ | (7) |
其中:α为斜率;β为截距;ε为残差,服从正态分布ε~N(0, δL2).
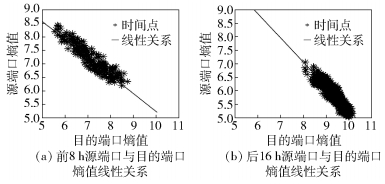
3.2 动态线性关系由于网络中的流量数据随时间的变化而变化,熵值之间的线性关系也略有不同.以源端口和目的端口熵值之间的线性关系为例,如图 4所示,图 4(a)是0点到8点熵值的线性关系,图 4(b)是9点到24点熵值的线性关系.两分图中线性表达式略有不同,图 4(a)线性关系的斜率和截距都较小,而图 4(b)线性关系的斜率和截距相对较大.因此,为了保证线性关系中参数α和β的实时性,提高检测率,采用动态的方式设定α和β.
|
图 4 不同时间段源端口与目的端口熵值线性关系 |
定义4 动态线性关系.设定时间窗口大小为N,时间尺度大小为T,当前检测的时间点为t,假设时间点t之前的N个聚合流不存在异常流量,使用该N个时间点的熵值序列建立动态线性关系.以源地址和目的地址熵值为例,当前时间点t上的线性表达式定义为
| $ {H_{sa,t}} = {\alpha _t}{H_{da,t}} + {\beta _t} + {\varepsilon _t} $ | (8) |
其中εt~N(0, δL, t2).
建立线性模型的关键是准确估计参数αt和βt的值,当实际值与线性表达式计算值之差的平方和最小时,可得到最佳的线性模型.假设实际值与计算值之差的平方和记为Q:
| $ \begin{array}{l} Q = \sum\limits_{t' = t - N}^{t - 1} {{{\left( {{H_{sa,t'}} - H_{sa,t'}^P} \right)}^2}} = \\ \sum\limits_{t' = t - N}^{t - 1} {{{\left[ {{H_{sa,t'}} - \left( {{\alpha _t}{H_{sa,t'}} + {\beta _t}} \right)} \right]}^2}} \end{array} $ | (9) |
其中:Hsa, t′P为根据线性表达式得出的源地址熵值,t-1≥t′≥t-N.因Q为非负值,所以Q的极小值即为最小值,分别对αt和βt求一阶偏导可得
| $ \begin{array}{*{20}{c}} {\left. \begin{array}{l} \frac{{\partial Q}}{{\partial {\alpha _t}}} = 0\\ \frac{{\partial Q}}{{\partial {\beta _t}}} = 0 \end{array} \right\} \Rightarrow }\\ {\left. \begin{array}{l} \sum\limits_{t' = t - N}^{t - 1} {\left[ {{H_{sa,t'}} - \left( {{\alpha _t}{H_{da,t'}} + {\beta _t}} \right)} \right]{H_{da,t'}}} = 0\\ \sum\limits_{t' = t - N}^{t - 1} {\left[ {{H_{sa,t'}} - \left( {{\alpha _t}{H_{da,t'}} + {\beta _t}} \right)} \right]} = 0 \end{array} \right\} \Rightarrow }\\ {\left. \begin{array}{l} {\alpha _t} = {{\bar H}_{sa,t'}} - {\beta _t}{{\bar H}_{da,t'}}\\ {\beta _t} = \frac{{N\sum\limits_{t' = t - N}^{t - 1} {{H_{da,t'}}{H_{sa,t'}}} - \sum\limits_{t' = t - N}^{t - 1} {{H_{da,t'}}} \sum\limits_{t' = t - N}^{t - 1} {{H_{sa,t'}}} }}{{N\sum\limits_{t' = t - N}^{t - 1} {H_{da,t'}^2} - {{\left( {\sum\limits_{t' = t - N}^{t - 1} {{H_{da,t'}}} } \right)}^2}}} \end{array} \right\}} \end{array} $ | (10) |
根据αt和βt的取值,计算残差的方差为
| $ \delta _{L,t}^2 = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {H_{sa,t'}^P - {H_{sa,t'}}} \right)}^2}} $ | (11) |
由于残差服从正态分布εt~N(0, δL, t2),设定偏离线性关系的阈值θL, t=±3δL, t.当时间点t的熵值实际值与根据线性表达式得出的计算值之间的差异超过所设定的阈值范围时,判断时间点t存在异常流量.
4 仿真实验实验使用的流量数据来自于某校园网节点.由于该校园的网络环境较为安全,所采集的数据几乎不存在异常流量,因此在验证所提方法的性能时需根据几种异常的特点模拟生成异常流量.采集2017年7月18日全天的校园网节点上共271万条数据作为背景流量,对背景流量进行预处理,去除噪声,在此背景流量中注入模拟生成的异常流量作为实验数据,采用Matlab平台实现流量异常检测方法的仿真.分为2个实验:一是使用所提方法实现流量异常检测的实验;二是将所提方法与现有方法进行对比的实验.
时间尺度大小T和时间窗口大小N的不同设置将产生不同的实验结果,设定合理的T和N才能使实验效果达到最佳.由于流量数巨大,时间尺度T的设置对方法的时延影响较大,设置的T越大,计算熵值时包含的数据量越大,实时检测的时延变大,而设置的T过小,导致计算熵值时包含的信息不充分,检测的准确率降低.因DDoS、扫描等攻击一般持续几分钟,在以下实验中都将T设定为1 min.通过实验对流量异常检测的准确率分析得出,当N=40时所提方法性能最佳,因此在实验一中将时间窗口设置为40,在实验二中通过设置不同的N,对比所提方法与现有方法在检测率、误检率和实时性方面的性能.检测率Pdete和误检率Pfalse定义如下:
| $ {P_{{\rm{dete}}}} = \frac{{检测出的异常点数量}}{{异常点总数}} \times 100\% $ | (12) |
| $ {P_{{\rm{false}}}} = \frac{{检测出的非异常点数量}}{{正常点总数}} \times 100\% $ | (13) |
在实验一中模拟生成了3万条异常流量,共30个异常时间点,其中包含了DDoS攻击、Flash Crowd、端口扫描、蠕虫病毒和网络扫描5种异常类型,将这3万条异常流量注入到背景流量中进行流量异常检测.注入异常流量后的熵值序列和熵值线性关系分别如图 5和图 6所示.由表 1可知,异常发生时,源端口熵值基本没有变化,因此无需在图 5中展示注入攻击流量后的源端口熵值序列.从图 5中可以看出,部分异常点较为明显,可以使用一级阈值直接检测出,如时间点328发生了端口扫描异常,熵值序列有明显的突变;也有部分异常点的熵值变化并不明显,无法设定一个合理的阈值检测这部分异常点,需要通过检测属性熵值之间的线性关系来确定是否发生异常,如时间点214发生了Flash Crowd,源地址、目的地址和目的端口的熵值变化都不明显,但由图 6可以看出该时间点明显偏离了源地址熵值和目的地址熵值的线性关系,因此从熵值变化程度上无法检测出的异常点可以通过熵值间的线性关系检测出来.
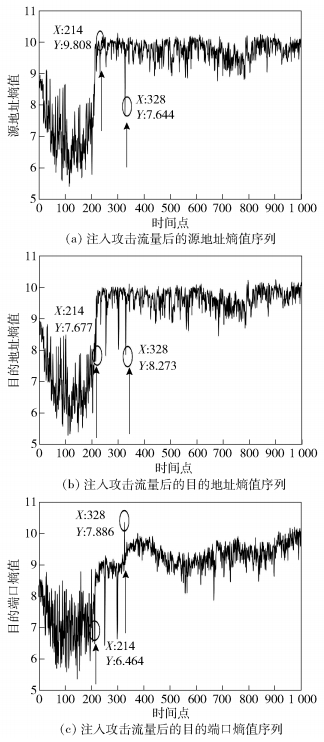
|
图 5 注入攻击流量后熵值序列 |
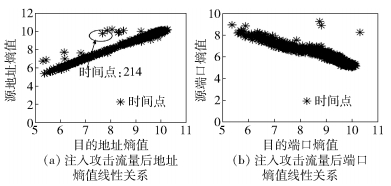
|
图 6 注入攻击流量后的熵值线性关系 |
使用所提方法进行异常检测时,首先在熵值的时间序列上对熵值变化程度进行检测,其中超过一级阈值的时间点共18个,可判断这18个时间点是出现异常的时间点;而超过二级阈值且低于一级阈值的时间点有22个,不能立即判断这22个时间点为异常点,需结合线性关系进一步分析,通过分析这22个时间点的熵值线性关系发现其中12个时间点偏离了线性关系,可判定这12个时间点为异常点.因此,所提方法共检测出30个异常点,检测率达到100%,且未有误判点,误检率为0.通过报警触发函数可正确判断30个异常点的异常类型,如表 2所示.
|
|
表 2 异常点的异常类型 |
由于实验一使用的数据中只有30个异常点,而较少的异常点对检测率和误检率的结果会产生一定的偶然性,因此实验二在实验一数据的基础上又注入了7万条异常流量,该实验数据中共包含了98个异常时间点.将所提方法与文献[2]的稳健线性回归流量异常检测方法(简称Robust-Linear方法)、文献[3]的基于小波分析和累积和的流量异常检测方法(简称Wave-Cusum方法)及文献[9]的基于Jenson-Shannon散度的流量异常检测方法(简称Jenson-Shannon方法)进行对比实验,验证所提方法在实时性和准确率方面的有效性.
1) 准确率对比实验
所提方法以及文献[2-3, 9]的方法都是在时间域上对流量异常进行检测,需设置时间窗口,而时间窗口N设置为不同大小时,检测率和误检率也会有所变化,检测率和误检率的实验结果分别如图 7、图 8所示.从图 7中可以看出,当时间窗口N≤25时所提方法的检测率虽然没有达到最佳,但当时间窗口N>25时检测率相对其他方法更佳.从图 8中可以看出,当时间窗口N≤10时所提方法的误检率较高,但当时间窗口N>10时所提方法的误检率迅速收敛,且低于其他方法.并且,当N=40时,所提方法的检测率达到最高,误检率降到最低.综上,当设定了合理的时间窗口后,所提方法较现有方法的准确率更好.
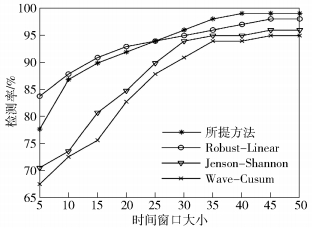
|
图 7 检测率对比 |
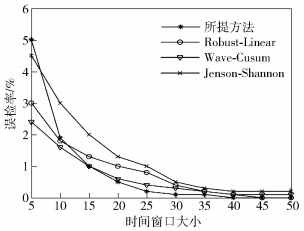
|
图 8 误检率对比 |
2) 实时性对比实验
时间窗口的选取对实时性有一定的影响,时间窗口越小,建模使用的数据量越少,建模时间也就越短,流量异常检测的实时性越好.因此,当时间窗口设置为不同值时,可记录所提方法、Robust-Linear方法、Wave-Cusum方法和Jenson-Shannon方法在对一个时间点上的实时流量进行检测时的运行时间,如图 9所示.从图 9中可以观察到,所提方法的运行时间要低于其他3种方法,因此所提方法具有较好的实时性.

|
图 9 实时性对比 |
笔者提出了一种基于熵和线性关系的两级流量异常检测方法,通过验证实验证明该方法是有效的,保证了实时性,提高了准确率,且可以通过熵值的变化方向识别出异常类型.下一步将在更精细粒度的层面上研究异常流量的行为特征,对出现异常的用户进行识别.
| [1] | Breier J, Branišová J. A dynamic rule creation based anomaly detection method for identifying security breaches in log records[J]. Wireless Personal Communications, 2015, 94(3): 1–15. |
| [2] | Wang Z, Yang J, Zhang S Z, et al. Robust regression for anomaly detection[C]//IEEE International Conference on Communications.[S. l.]: IEEE, 2017: 1-6. |
| [3] | Callegari C, Giordano S, Pagano M, et al. Combining wavelet analysis and CUSUM algorithm for network anomaly detection[C]//IEEE International Conference on Communications.[S. l.]: IEEE, 2012: 1091-1095. |
| [4] | Nychis G, Sekar V, Andersen D G, et al. An empirical evaluation of entropy-based traffic anomaly detection[C]//Internet Measurement Conference.[S. l.]: ACM, 2008: 151-156. |
| [5] | Callegari C, Giordano S, Pagano M, et al. Entropy-based network anomaly detection[C]//International Conference on Computing, Networkingand Communications.[S. l.]: IEEE, 2017: 334-340. |
| [6] | Navaz A S S, Sangeetha V, Prabhadevi C, et al. Entropy based anomaly detection system to prevent DDoS attacks in cloud[J]. International Journal of Computer Applications, 2013, 62(15): 42–47. doi: 10.5120/10160-5084 |
| [7] | Huo X, Lü C, Pei P, et al. Smart grid communication network traffic anomaly detection based on entropy analysis[C]//IEEE International Conference on Computer and Communications.[S. l.]: IEEE, 2017: 1082-1086. |
| [8] | Salem O, Naït-abdesselam F, Mehaoua A, et al. Anomaly detection in network traffic using Jensen-Shannon divergence[C]//IEEE International Conference on Communications.[S. l.]: IEEE, 2012: 5200-5204. |
| [9] |
范晓诗, 李成海. 加权条件熵在异常检测中的应用[J]. 计算机应用研究, 2014, 31(1): 203–205.
Fan Xiaoshi, Li Chenghai. Application of weighted conditional entropy in anomaly detection[J]. Application Research of Computers, 2014, 31(1): 203–205. doi: 10.3969/j.issn.1001-3695.2014.01.047 |
| [10] | 李中魁.基于动态阈值的网络流量异常检测方法研究与实现[D].成都: 电子科技大学, 2010. |
| [11] | Iordache M, Jouet S, Marnerides A K, et al. Distributed, multi-level network anomaly detection for datacentre networks[C]//2017 IEEE International Conference on Communications.[S. l.]: IEEE, 2017: 1-6. |


