针对传统聚类算法难以处理大规模数据和对噪声数据敏感等问题,基于模糊C有序均值聚类算法(FCOM),结合single-pass和online增量架构,分别提出了single-pass模糊C有序均值聚类算法(SPFCOM)和online模糊C有序均值聚类算法(OFCOM).SPFCOM和OFCOM算法首先对FCOM算法加权,然后以数据块为单位对数据集合进行增量式处理.实验结果表明,相较于对比算法,SPFCOM和OFCOM算法在聚类准确率方面得到了提高,还具有更强的鲁棒性.
Because traditional clustering algorithms are difficult to deal with large-scale data and sensitive to noise data, based on the Fuzzy C-ordered-means clustering (FCOM) algorithm, we propose a single-pass fuzzy C-ordered clustering algorithm, named SPFCOM, and an online fuzzy C-ordered clustering algorithm, named OFCOM, by combining single-pass and online incremental architectures respectively. These two algorithms weight the FCOM algorithm, and incrementally process the large-scale data chunk by chunk. Experimental results show that, compared with other similar prominent algorithms, the SPFCOM and OFCOM algorithms can achieve higher accuracy and better robustness.
模糊C均值算法(FCM, fuzzy C-means clustering)[1]是模糊聚类的代表性算法,得到了广泛应用.然而,该算法对噪声比较敏感,极易造成聚类精度的下降.于是,在FCM基础上,衍生出许多改进算法,其改进思路一般包括2种,即采用Huber的M-estimators[2]或Yager的OWA运算符[3]. 2016年,Leski提出了模糊C有序均值算法(FCOM, fuzzy C-ordered-means clustering)[4],该算法结合了FCM算法和有序加权平均运算符,将M-estimator和OWA运算符同时应用于模糊聚类中,通过排序提高了算法的健壮性和鲁棒性.但是,与多数传统聚类算法类似,FCOM算法难以处理大规模数据或数据流.为了解决此类问题,Hore等[5-6]提出了SPFCM(single-pass fuzzy C-means)和OFCM(online fuzzy C-means) 2种增量算法,采用的single-pass和online框架逐渐发展成为增量聚类算法研究中的重要方法. single-pass方法的基本思想是将数据分成若干数据块(chunk),对每个数据块依次进行聚类,聚类后得到的质心参与到下一个数据块的聚类运算中,直至得到最终结果;online方法则采用并行方式,针对每个数据块聚类之后得到的质心再次聚类,进而得到最终的聚类结果. SPFCM和OFCM 2种算法虽然可以处理大规模数据,但依然是类FCM算法,仍然对噪声数据比较敏感.
基于single-pass和online增量框架分别提出一种模糊C有序均值聚类算法:SPFCOM算法(single-pass fuzzy C-ordered-means clustering)和OFCOM算法(online fuzzy C-ordered-means clustering). SPFCOM和OFCOM算法同时继承了FCOM和增量算法的优点:一方面通过采用FCOM的思想保证算法的鲁棒性;另一方面通过采用增量方法可有效处理大规模数据.
1 相关工作 1.1 FCOM算法FCOM算法的目标函数为
| $ J\left( {U,V} \right) = \sum\limits_{c = 1}^C {\sum\limits_{i = 1}^N {{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}D\left( {{x_i},{v_c}} \right)} } $ | (1) |
其中:参数βci表示第i个数据对第c个簇的典型性,D(xi, vc)可由Hcij和Ecij计算得出,即
| $ D\left( {{x_i},{v_c}} \right) = \sum\limits_{j = 1}^K {D\left( {{x_{ij}},{v_{cj}}} \right)} = \sum\limits_{j = 1}^K {{H_{cij}}{{\left( {{E_{cij}}} \right)}^2}} $ |
该目标函数受限于
| $ \mathop \forall \limits_{\begin{array}{*{20}{c}} {1 \le c \le C}\\ {1 \le i \le N} \end{array}} {u_{ci}} \in \left[ {0,1} \right] $ | (2) |
| $ \sum\limits_{c = 1}^C {{\beta _{ci}}{u_{ci}}} = {F_i} $ | (3) |
其中Fi表示第i个数据对于所有簇的综合典型性.
1.2 基于FCM的增量模糊聚类single-pass和online是聚类研究中常用的2种增量化思想,最早分别应用在SPFCM算法[5]与OFCM算法[6]中.这2种算法均以WFCM (weighted fuzzy C-means clustering)为基础.
1.2.1 WFCM算法WFCM是加权的FCM算法,即在FCM算法迭代过程中,对得到的质心进行加权,为重要性高的对象赋予较高权重.假设目标数据集为X=[x1, x2, …, xn],则WFCM的目标函数JWFCM为
| $ {J_{{\rm{WFCM}}}} = \sum\limits_{c = 1}^C {\sum\limits_{i = 1}^N {{w_i}u_{ci}^m{{\left\| {{x_i} - {v_c}} \right\|}^2}} } $ | (4) |
其中wi为第i个数据的权重.通过拉格朗日乘子法可得uci和vc的迭代公式为
| $ {u_{ci}} = \frac{{{{\left\| {{x_i} - {v_c}} \right\|}^{\frac{{ - 2}}{{m - 1}}}}}}{{\sum\limits_{k = 1}^C {{{\left\| {{x_i} - {v_k}} \right\|}^{\frac{{ - 2}}{{m - 1}}}}} }} $ | (5) |
| $ {v_c} = \frac{{\sum\limits_{i = 1}^N {{w_i}u_{ci}^m{x_i}} }}{{\sum\limits_{i = 1}^N {{w_i}u_{ci}^m} }} $ | (6) |
SPFCM基于WFCM算法进行聚类.将所有对象的权重初始化为1,即wdata=[1, 1, …, 1]T,假定数据集划分为h个数据块,即X=[X1, X2, …, Xh],Xt表示第t个数据块(1≤t≤h).对X1进行聚类时,得到质心Δ=[v1, v2, …, vc]及其权重wc=
OFCM同样基于WFCM算法进行聚类.首先对每个数据块单独聚类,然后将每个数据块得到的质心和权重组成一个总的数据块和权重矩阵,再次聚类得到最终质心,其中每个数据块聚类后的权重表示为w=[w11, w21, …, wc1, w12, w22, …, wc2, …, w1h, w2h, …, wch].
2 增量式模糊C有序均值聚类算法分别基于single-pass和online增量框架,提出了增量式模糊C有序均值聚类算法:SPFCOM和OFCOM.在SPFCOM和OFCOM算法中,首先设计加权的FCOM算法WFCOM(weighted fuzzy C-ordered-means clustering),其目标函数为
| $ J\left( {U,V} \right) = \sum\limits_{c = 1}^C {\sum\limits_{i = 1}^N {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}D\left( {{x_i},{v_c}} \right)} } $ | (7) |
约束条件为
| $ \mathop \forall \limits_{\begin{array}{*{20}{c}} {1 \le c \le C}\\ {1 \le i \le N} \end{array}} {u_{ci}} \in \left[ {0,1} \right] $ | (8) |
| $ \sum\limits_{c = 1}^C {{\beta _{ci}}{u_{ci}}} = {F_i} $ | (9) |
最小化该目标函数,得到uci和vcj的迭代公式为
| $ \mathop \forall \limits_{\begin{array}{*{20}{c}} {1 < i < N}\\ {1 < c < C} \end{array}} {u_{ci}} = \frac{{{F_i}D{{\left( {{x_i},{v_s}} \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{t = 1}^C {{\beta _{ti}}DD{{\left( {{x_i},{v_t}} \right)}^{\frac{1}{{1 - m}}}}} }} $ | (10) |
| $ \mathop \forall \limits_{\begin{array}{*{20}{c}} {1 < c < C}\\ {1 < j < K} \end{array}} {v_{cj}} = \frac{{\sum\limits_{i = 1}^N {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}{x_{ij}}} }}{{\sum\limits_{i = 1}^N {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}} }} $ | (11) |
SPFCOM算法在WFCOM基础上,采用single-pass增量框架进行实现.具体实现过程为:首先初始化权重,将所有数据对象的权重初始化为1,即w=[1, 1, …, 1]T,并假设数据集划分为h个数据块,即X=[X1, X2, …, Xh].
1) 当t=1时,聚类过程与FCOM算法类似,可得质心矩阵Δ1=[v1, v2, …, vc]和相应的权重矩阵:
| $ {{\mathit{\boldsymbol{w'}}}_c} = \sum\limits_{i = 1}^{{n_1}} {\left( {{u_{ci}}} \right){w_i}} $ | (12) |
其中1≤c≤C,wi=1,1≤i≤n1,nt为第t个数据块的对象个数.
最小化目标函数,对数据块X1聚类后隶属度uci和质心vcj的公式为
| $ {u_{ci}} = \frac{{{F_i}D{{\left( {{{x'}_i},{v_c}} \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{t = 1}^C {{\beta _{ti}}D{{\left( {{{x'}_i},{v_t}} \right)}^{\frac{1}{{1 - m}}}}} }} $ | (13) |
| $ {v_{cj}} = \frac{{\sum\limits_{i = 1}^{{n_1}} {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}{x_{ij}}} }}{{\sum\limits_{i = 1}^{{n_1}} {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}} }} $ | (14) |
其中1≤j≤K.
2) 当t>1时,将数据块Xt-1的质心Δt-1加权后加入数据块Xt中,得到新的数据块Xt′=[Δt-1, Xt].对新的数据块进行聚类,相应权重更新为
| $ {{\mathit{\boldsymbol{w'}}}_c} = \sum\limits_{i = 1}^{c + {n_t}} {\left( {{u_{ci}}} \right)\left[ {{{\mathit{\boldsymbol{w'}}}_c},{\mathit{\boldsymbol{w}}_c}} \right]} $ | (15) |
其中1≤c≤C,wc=1,1≤i≤nt.
最小化目标函数,对数据块Xt聚类后得到的隶属度uci和质心vcj的公式为
| $ {u_{ci}} = \frac{{{F_i}D{{\left( {{{x'}_i},{v_c}} \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{t = 1}^C {{\beta _{ti}}D{{\left( {{{x'}_i},{v_t}} \right)}^{\frac{1}{{1 - m}}}}} }} $ | (16) |
| $ {v_{cj}} = \frac{{\sum\limits_{i = 1}^{{n_t} + c} {{{w'}_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}{{x'}_{ij}}} }}{{\sum\limits_{i = 1}^{{n_t} + c} {{{w'}_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}} }} $ | (17) |
其中1≤j≤K,1≤i≤nt+c.
SPFCOM算法的聚类过程可用伪码描述如下.
1 确定簇数目c和权重指数m∈(1, ∞),选择ε-敏感性相异性度量方法,初始化隶属度矩阵U(0),βci=1,Hcij=1,Fi=1,设置迭代次数z=1;
2 将数据集划分为h块,即X=[X1, X2, …, Xh],初始化权重w=[1, 1, …, 1]T.设置t=1;
3 利用式(14)或(17)更新簇中心矩阵V(z);
4 计算残差Ecij;
5 对残差Ecij进行排序;
6 计算综合典型性参数Fi;
7 利用式(13)或(16)计算隶属度矩阵U(z);
8 ① t < h:若‖U(z)-U(z-1)‖F>ξ,令z←z+1并转到步骤3;否则把质心和权重添加到下一个数据块的数据矩阵和权重矩阵中,获得新的数据块矩阵和权重矩阵,令t←t+1并且转到步骤3;
② t=h:若‖U(z)-U(z-1)‖F>ξ,令z←z+1并转到步骤3;否则结束.
2.2 OFCOM算法基于WFCOM算法,采用online增量框架,设计了OFCOM算法.在OFCOM算法中,同样地,初始化权重得到w=[1, 1, …, 1]T,并将h个数据块记为X=[X1, X2, …, Xh].
1) 对h个数据块依次聚类,得到质心矩阵Δt=[v1, v2, …, vc]和相应权重矩阵:
| $ \mathit{\boldsymbol{w}}_c^t = \sum\limits_{i = 1}^{{n_t}} {{u_{ci}}{\mathit{\boldsymbol{w}}_i}} $ | (18) |
其中1≤c≤C,wi=1,1≤i≤nt,nt为第t个数据块的对象个数.
最小化目标函数,对数据块Xt聚类后隶属度uci和质心vcj的表达式为
| $ {u_{ci}} = \frac{{{F_i}D{{\left( {{x_i},{v_c}} \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{t = 1}^C {{\beta _{ti}}D{{\left( {{x_i},{v_t}} \right)}^{\frac{1}{{1 - m}}}}} }} $ | (19) |
| $ {v_{cj}} = \frac{{\sum\limits_{i = 1}^{{n_t}} {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}{x_{ij}}} }}{{\sum\limits_{i = 1}^{{n_t}} {{w_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}} }} $ | (20) |
其中1≤j≤K.
2) 将每个数据块聚类后得到的质心和权重分别组成总的数据矩阵X′和权重矩阵w′,并对这2个矩阵再次聚类得到最终隶属度矩阵和质心矩阵.分别记数据矩阵X′和权重矩阵w′为X′=[Δ1, Δ2, …, Δh]和w′=[w11, w21, …, wc1, w12, w22, …, wc2, …, w1h, w2h, …, wch].
最小化目标函数,得到隶属度和质心的表达式:
| $ {u_{ci}} = \frac{{{F_i}D{{\left( {{{x'}_i},{v_c}} \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{t = 1}^C {{\beta _{ti}}D{{\left( {{{x'}_i},{v_t}} \right)}^{\frac{1}{{1 - m}}}}} }} $ | (21) |
| $ {v_{cj}} = \frac{{\sum\limits_{i = 1}^{{n_x}} {{{w'}_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}{{x'}_{ij}}} }}{{\sum\limits_{i = 1}^{{n_x}} {{{w'}_i}{\beta _{ci}}{{\left( {{u_{ci}}} \right)}^m}{H_{cij}}} }} $ | (22) |
其中1≤j≤K,1≤i≤nx,nx为数据个数.
OFCOM算法的聚类过程可用伪码描述如下.
1 确定簇数目c和权重指数m∈(1, ∞).选择ε—敏感性相异性度量方法.初始化隶属度矩阵U(0),βci=1,Hcij=1,Fi=1,质心矩阵l和权重矩阵m,且设置迭代次数z=1;
2 将数据集划分为h块,即X=[X1, X2, …, Xh],初始化权重w=[1, 1, …, 1]T.设置t=1;
3 利用式(20)或(22)更新簇中心矩阵V(z);
4 计算残差Ecij;
5 对残差Ecij进行排序;
6 计算综合典型性参数Fi;
7 利用式(19)或(21)计算隶属度矩阵U(z);
8 ① t < =h:若‖U(z)-U(z-1)‖F>ξ,令z←z+1并转到步骤3;否则把质心和权重添加到质心矩阵l和权重矩阵m中,令t←t+1并转到步骤3;
② t>h:若‖U(z)-U(z-1)‖F>ξ,令z←z+1并转到步骤3;否则结束.
3 实验与分析 3.1 数据集介绍实验数据集均来自于UCI数据库,各数据集具体信息见表 1.为定量评估聚类结果的准确性,采用F度量(F-measure)[7]和熵(entropy)2种评价标准.
|
|
表 1 实验数据集简介 |
为了验证SPFCOM和OFCOM算法的效果,在UCI数据库的数据集上进行了2组实验:第1组实验重点考查算法的准确率,并与SPFCM、SPHFCM(single-pass hyperspherical fuzzy C means)[8]、OFCM和OHFCM(online hyperspherical fuzzy C means)[8]算法进行了比较;第2组实验验证算法的鲁棒性.
1) 算法准确率
实验中,通过UCI数据库的6个数据集评估算法的准确率.为便于比较,采用与FCOM算法相同的参数设置.将3种single-pass算法(SPFCM、SPHFCM、SPFCOM)和3种online算法(OFCM、OHFCM、OFCOM)分别进行比较.为了考查算法在不同数据块块大小条件下的表现,将数据块大小分别设定为各数据集样本总数的5%、10%、20%和50%.各实验运行10次后取平均值,实验结果如图 1~4所示.

|
图 1 SPFCM、SPHFCM和SPFCOM算法的F度量对比 |

|
图 2 SPFCM、SPHFCM和SPFCOM算法的熵对比 |
|
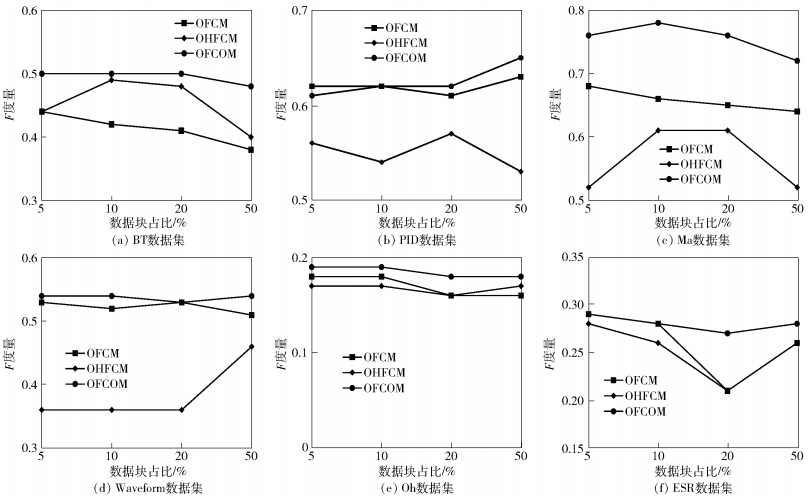
图 3 OFCM、OHFCM和OFCOM算法的F度量对比 |
|
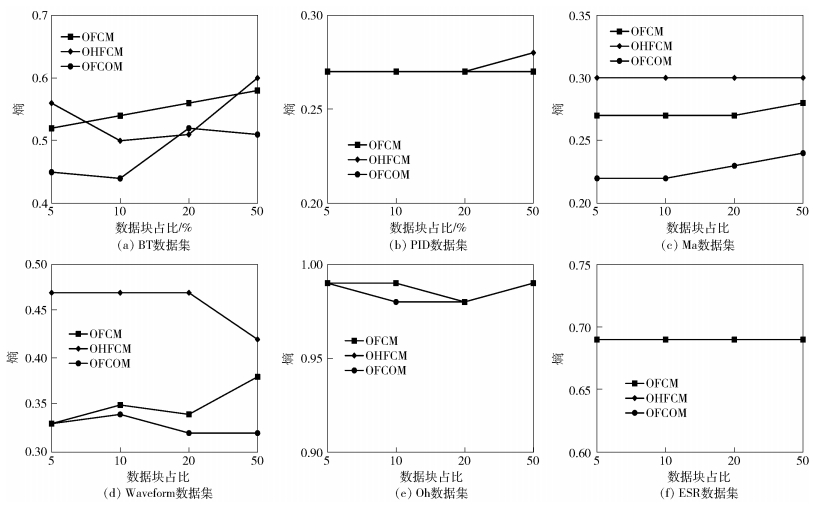
图 4 OFCM、OHFCM和OFCOM算法的熵对比 |
从图 1~4可以看出,在各数据集的实验结果中,当数据块大小分别取5%、10%、20%和50%时,SPFCOM和OFCM算法均可以取得较高的聚类准确率,总体表现较优,用F度量和熵表示的平均聚类结果见表 2.
|
|
表 2 算法准确率比较 |
通过该组实验可知,SPFCOM算法与OFCOM算法在实验数据集上获得了比对比算法更高或相当的聚类准确率,且部分数据集上提升幅度较为明显.
2) 算法鲁棒性
为了验证算法的鲁棒性,第2组实验在BT数据集上测试噪声数据对SPFCOM与OFCOM算法的影响.将数量为BT数据集样本总数10%、20%、30%和40%的噪声样本分别添加到数据集中,实验结果如图 5所示.
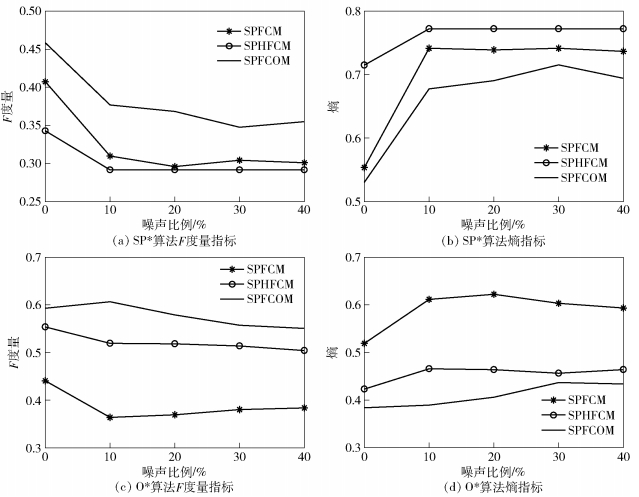
|
图 5 噪声对聚类的影响 |
图 5(a)和图 5(b)分别对比了SPFCM、SPHFCM和SPFCOM 3种算法在F度量和熵两项指标上的表现.当噪声数据逐渐增多时,3种single-pass算法的F度量指标逐渐下降.在加入10%的噪声样本时,3种算法的F度量值均下降较多,其中SPFCM算法的下降幅度较大,而SPHFCM算法直接降至该算法的最低点,此时SPFCOM算法的F度量指标仍比其他2种算法分别提高了6.6%和8.5%;继续加入噪声样本后,3种算法的F度量指标则趋于稳定;在噪声样本增加至40%后,SPFCOM算法F度量指标的提高幅度分别为5.3%和6.3%.在熵指标方面,如图 5(b),可以得到与F度量指标类似的实验结果;在加入10%的噪声点时,3种算法的熵值上升较多;继续添加噪声样本后,熵指标趋于平稳,直至噪声样本占比达到40%;在此过程中,SPFCOM算法的熵指标均低于对比算法.
图 5(c)和图 5(d)中给出了OFCM、OHFCM和OFCOM 3种算法的对比.从图 5(c)可以看出,当噪声样本增多时,3种算法的F度量指标逐渐降低:当加入10%噪声样本时,OFCM和OHFCM算法的F度量指标均大幅降低,而OFCOM算法则变化较小,其F度量值相比其他2种算法分别高出24.2%和8.7%;继续加入噪声样本,3种算法的F度量指标则渐趋平稳;噪声样本数量达到40%时,OFCOM算法F度量值的提高幅度分别为16.6%和4.6%.在图 5(d)给出的熵指标对比中,可得到相似结论:当加入10%的噪声样本时,OFCM和OHFCM算法的熵指标逐渐上升,而OFCOM算法则变化较小,在10%处其熵值相比其他2种算法分别降低22.2%和7.6%;继续添加噪声样本,3种算法的熵指标则比较平稳,而OFCOM算法的熵指标一直表现最优;最终在40%噪声样本点处,OFCOM的熵值比对比算法分别低15.9%和3.0%.
本组实验结果表明,当数据集中存在噪声时,SPFCOM和OFCOM具有较好的鲁棒性.
4 结束语大数据时代背景下,是否具备处理大规模数据的能力并具备较高的鲁棒性,是衡量一个聚类算法聚类表现的重要标准.鉴于传统算法在这2方面的劣势,提出了2种增量式模糊C有序均值聚类算法,即SPFCOM与OFCOM.这2种算法一方面引入排序机制,有效降低了对噪声数据的敏感度;另一方面分别采用了single-pass和online增量架构,能有效处理大规模数据.为了评估算法的聚类效果,在6个真实数据集上进行了实验.实验结果表明,相较于对比算法,SPFCOM与OFCOM可以获得更高的聚类准确率,同时具有更强的鲁棒性.
| [1] | Bezdek J C, Ehrlich R, Full W. FCM:the fuzzy C means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2): 191–203. |
| [2] | Huber P J. Robust statistics[J]. Journal of the American Statistical Association, 1981, 78(381): 1248–1251. |
| [3] | Yager R R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking[J]. Readings in Fuzzy Sets for Intelligent Systems, 1993, 18(1): 80–87. |
| [4] | Leski J M. Fuzzy c-ordered-means clustering[J]. Fuzzy Sets & Systems, 2016(286): 114–133. |
| [5] | Hore P, Hall L O, Goldgof D B. Single pass fuzzy C means[C]//IEEE International Conference on Fuzzy Systems. London: IEEE, 2007: 1-7. |
| [6] | Hore P, Hall L O, Goldgof D B, et al. Online fuzzy C means[C]//NAFIPS 2008. New York: IEEE, 2008: 1-5. |
| [7] | Maratea A, Petrosino A, Manzo M. Adjusted F-measure and kernel scaling for imbalanced data learning[J]. Information Sciences, 2014, 257(2): 331–341. |
| [8] | Mei J P, Wang Y, Chen L, et al. Incremental fuzzy clustering for document categorization[C]//IEEE International Conference on Fuzzy Systems. Beijing: IEEE, 2014: 1518-1525. |


