2. 中国科学院信息工程研究所, 北京 100093;
3. 中国科学院大学 网络空间安全学院, 北京 100049;
4. 北京印刷学院 新媒体学院, 北京 102600
提出了一种基于极化多维星座的正交频分复用(OFDM)物理层安全通信机制,通过高维星座设计,可以有效地加密调制信息,保护无线通信的调制信息不被发现,从而保证无线通信的安全.在此基础上,推导并仿真了系统误码率性能和频谱利用率.仿真结果证明,OFDM极化多维星座调制方案可以有效防止窃听者获取调制信息,并且其误符号率及频谱效率都显著优于传统OFDM-QAM调制.
2. Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China;
3. School of Cyber Security, Chinese Academy of Sciences, Beijing 100049, China;
4. School of New Media, Beijing Institute of Graphic Communication, Beijing 102600, China
An orthogonal frequency division multiplexing (OFDM) multi-carrier physical layer secure communication mechanism based on multi-dimensional constellation was presented, which can effectively prevent the modulation information of wireless communication from being eavesdropped, therefore, the security communication is guaranteed. Based on multi-dimensional constellation, the system symbol error rate performance and spectrum utilization are derived and simulated. Simulations show that the multi-carrier polarization state-amplitude-phase modulation scheme can effectively prevent the eavesdropper from obtaining the modulation information, and its symbol error rate and spectral efficiency are significantly better than the traditional OFDM-QAM modulation.
随着移动通信技术的高速发展,保护用户通信的私密性已成为当前移动通信系统所面临的紧迫问题[1].目前,无线通信物理层安全方案主要有3种:基于人工噪声[2-3]、基于多天线随机加权[4-5]以及基于星座图变换[6-7].这些物理层加密算法可极大提升移动通信系统物理层的安全性,但信道差异较小时,上述算法的安全性能则无法保障.
由于无线极化信道容易受天线及信道散射体空域特性等多种因素影响而具有独特随机性,这种随机性为物理层安全提供了另一种可能.极化调制[8]在无线通信物理层安全领域展现出巨大应用潜力[9-12],目前主要侧重极化调制在物理层安全方面应用的研究,或者致力于极化调制通信性能的研究,而将极化调制和已有的调制技术结合的研究很少.
因此,笔者提出了一种基于极化多维星座调制的正交频分复用(OFDM,orthogonal frequency division multiplexing)物理层安全通信机制.首先,通过引入极化状态调制构建多维星座,打破传统OFDM无线通信系统二维星座结构所呈现的调制特征,消除信号的调制信息特征;其次,利用极化状态对无线信道去极化效应的敏感性,在星座结构中引入去极化效应,使得星座具有独特的不可复制性,提供更好的加密性能.此外,所提出的安全通信机制可完全兼容传统的OFDM通信系统,并且可以进一步提高OFDM通信系统的频谱效率.
1 基于极化状态调制的物理层安全模型无线传输中,安全传输系统模型如图 1所示.发送端Alice、合法接收端Bob和窃听端Eve均配置有相同的正交双极化天线用于信号发送和接收,采用时分双工方式进行通信. Alice和Bob之间的信道称为合法信道,记作HAB;Alice和Eve之间的信道称为窃听信道,记作HAE.在信道相干时间内,合法通信双方可获得相同的信道信息,即信道满足短时互易性.当Eve与Alice或Bob的距离相差半个信号波长以上时,HAE和HAB可看作是不相关的[1],实际窃听信道模型中,很容易满足该条件,即信道具有唯一性.

|
图 1 安全传输系统模型 |
通信过程如下:合法通信双方首先发送包含有导频序列的通信请求,获得当前的合法信道信息HAB,然后进行安全通信.在Alice端,对传输数据进行高维星座映射,映射规则与合法信道信息HAB有关.在Bob端,对接收信息进行高维星座解映射,即可恢复出原始信息.
对于极化调制信号,信道去极化效应的随机性会增加合法信道的随机性.通过引入极化多维星座映射,在窃听端无法获得HAB时,极化高维星座图比传统星座图会受到更严重扰乱. HAB随机性的增强和星座映射规则复杂度的增加,使得窃听端采用盲信号处理技术恢复正常信息的难度增加,从而保障无线通信的物理层安全传输.
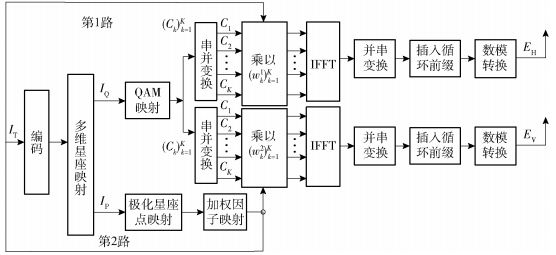
2 OFDM极化多维星座调制系统基带OFDM极化多维星座调制系统如图 2所示.首先对发射信息IT进行编码得到比特序列IC;然后按照设计的多维星座映射规则,将IC映射为IQ和IP两部分,以分别再映射为二维欧氏空间复数星座点(如图 2中第1路所示)和三维Stokes空间极化星座点(如图 2中第2路所示).
|
图 2 基带OFDM极化多维星座调制系统 |
在第1路中,首先将IQ映射为正交振幅调制(QAM, quadrature amplitude modulation)星座点;然后复制第1路得到的QAM星座点,并分成相同的两支路;之后对每一支路QAM星座点进行串并变换,并分别对两支路中相同的QAM星座点乘以加权因子Wk1和Wk2;最后根据OFDM链路的处理方法,分别对两支路的QAM星座点进行逆快速傅里叶变换(IFFT, inverse fast Fourier transform)、并串变换、插入循环前缀、数模转换,并通过正交双极化天线发射出去,将正交双极化天线发射出去的信号分别表示为EH和EV.
在第2路中,首先通过极化状态调制单元将IP映射为MP阶极化状态星座(Pi)i=1MP,从而IP转化为K个极化状态序列(Pk)k=1K(Pk∈(Pi)i=1MP);然后将每一个极化状态映射为一组加权因子:[Wk1,Wk2],表示为
| $ \left[ {\begin{array}{*{20}{c}} {W_k^1}\\ {W_k^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sin {\delta _k}{{\rm{e}}^{{\rm{j}}{\varphi _{k,{\rm{V}}}}}}}\\ {\cos {\delta _k}{{\rm{e}}^{{\rm{j}}{\varphi _{k,{\rm{H}}}}}}} \end{array}} \right] $ | (1) |
其中:sin δk、cos δk分别为垂直极化状态和水平极化状态的归一化幅度权重因子,
根据式(1),可将EH和EV分别表示为
| $ {E_{\rm{H}}} = \sum\limits_{k = 1}^K {W_k^1{A_k}{{\rm{e}}^{\left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}{f_k}t + {\varphi _0}\left( k \right)} \right]}}} $ | (2) |
| $ {E_{\rm{V}}} = \sum\limits_{k = 1}^K {W_k^2{A_k}{{\rm{e}}^{\left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}{f_k}t + {\varphi _0}\left( k \right)} \right]}}} $ | (3) |
其中Ak、
综上分析,可以发现整个基带极化状态调制通过第2路以数字信号处理的方式实现,即第2路幅度缩放tan δk,相位滞后
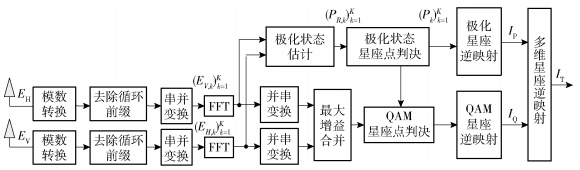
OFDM极化多维星座调制系统解调方法如图 3所示.
|
图 3 OFDM极化多维星座解调系统 |
根据图 3所示,首先将垂直/水平双极化天线接收到的信号进行模数转换、去除循环前缀及串并变换,得到两组样本序列(EV, k)k=1K和(EH, k)k=1K;然后分别对(EV, k)k=1K和(EH, k)k=1K进行快速傅里叶变换(FFT, fast Fourier transform),并分成相同的两路分量分别用于极化状态调制解调和QAM解调.
对于极化状态解调,通过计算(EV, k)k=1K和(EH, k)k=1K间的幅度比和相位差可以得到对应的信号极化状态(PR, k)k=1K,并利用(PR, k)k=1K判决相应的极化状态星座点(Pk)k=1K,最后根据极化状态星座逆映射得到所承载的二进制序列IP.
对于QAM解调,为获得最大分集增益,首先将两路并串变换分出的垂直极化分量和水平极化分量进行合并;然后根据极化状态星座点判断相应QAM星座点所位于的二维欧氏空间、受到的附加相位及星座点位置;最后利用QAM星座逆映射,从每个QAM星座点中恢复二进制序列IQ.
最后根据发射端基于置信度的多维星座映射规则,利用IP和IQ恢复发送信息IT.
3 安全极化高维星座设计在OFDM极化多维星座调制系统中,每个子载波的极化状态、幅度及相位都承载着发射信息.因此,每个子载波被调制的特征为幅值Ak、相位
| $ \mathit{\Gamma } = \left( {{A_k},{\varphi _0}\left( k \right),{\delta _k},{\varphi _{k,{\rm{V}}}},{\varphi _{k,{\rm{H}}}}} \right) $ | (4) |
又
| $ \mathit{\Gamma } = \left( {{A_k},{\varphi _0}\left( k \right),{\delta _k},{\varphi _k},{\varphi _{k,{\rm{H}}}}} \right) $ | (5) |
其中:Ak和

|
图 4 附加相位引入的复数星座旋转 |
I和Q为欧氏空间的相互正交的坐标轴,受
|
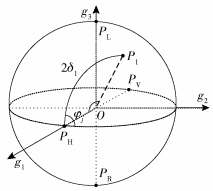
图 5 庞加莱极化球 |
g1、g2和g3为Stokes空间3个相互正交的坐标轴,Pk的坐标为(cos 2δk, sin 2δkcos
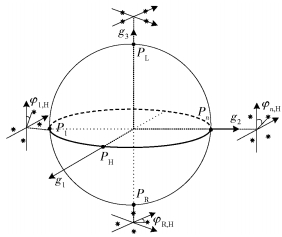
综合上述分析,则Γ所对应的多维星座空间由二维欧氏空间与三维Stokes空间所构成,如图 6所示.
|
图 6 多维星座空间模型 |
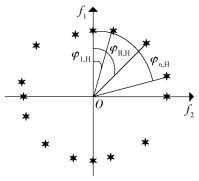
根据图 6所示,所有的极化状态星座点由黑色点表示,都分布在庞加莱球面上.对于每一个极化状态星座点,又连接着一个二维欧氏空间,上面分布着QAM星座点.根据该多维星座空间模型,可以发现每一个二维欧氏空间只与一个极化状态星座点连接,而且这些欧氏空间相互没有重叠交叉.所以,即便是不同二维欧氏空间相同位置上的QAM星座点,由于它们连接着2个不同的极化状态星座点,从而在多维空间中是2个不同的星座点.因此,若对于不同的极化状态星座点引入不同的附加相位,则每个极化状态星座点所连接的二维欧氏空间QAM星座图都会整体旋转一个不同的固定角度,如图 6中,与P1相连接的QAM星座图会整体旋转
|
图 7 忽略极化状态后的QAM星座图结构 |
综上所述,可以发现QAM星座点分布与极化星座点分布密切相关,并且可由Γ=(Ak,
由OFDM极化多维星座调制方案可知,子载波的极化状态与幅度-相位分别传输不同的二进制序列,因此每个子载波的误符号率Sk由两部分构成:利用极化状态传输信息引入的误符号和利用幅度-相位传输信息引入的误符号,分别记为SP, k和SQ, k,即
| $ {S_k} = \frac{{{S_{{\rm{P}},k}}{N_{{\rm{SPK}}}} + {S_{{\rm{Q}},k}}{N_{{\rm{SQK}}}}}}{{{N_{{\rm{SPK}}}} + {N_{{\rm{SQK}}}}}} $ | (6) |
其中NSPK及NSQK分别为极化状态和幅度-相位2种调制方式实现的符号率.
受加性高斯白噪声影响,接收极化状态(PR, k)k=1K在庞加莱球上的分布可用如下关于接收信噪比G的联合概率分布函数来描述:
| $ \begin{array}{*{20}{c}} {f\left( {{t_k},{r_k}} \right) = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\sin {t_k}\left( {{{\rm{e}}^{G\left( {1 - \cos {t_k}} \right)/2}}} \right) \times }\\ {\left[ {1 + G\left( {1 + \cos {t_k}} \right)/2} \right]} \end{array} $ | (7) |
其中tk和rk为将PR, k作为庞加莱球g3轴与球面的焦点时PR, k所对应的纬度与经度.利用式(7),加性高斯白噪声信道下MP阶极化状态调制的误符号率函数SP, k可表示为
| $ {S_{{\rm{P}},k}} = \frac{1}{{{M_{\rm{P}}}}}\sum\limits_{k = 1}^{{M_{\rm{P}}}} {{e_k}} $ | (8) |
其中ek为关于极化状态星座每个接收星座点PR, k的误符号率函数:
| $ {e_k} = \left\{ \begin{array}{l} \int_{{\rm{ \mathsf{ π} }} - {\theta _0}}^{\rm{ \mathsf{ π} }} {\int_0^{2{\rm{ \mathsf{ π} }}} {f\left( {{t_k},{r_k}} \right){\rm{d}}{r_k}{\rm{d}}{t_k}} } + \\ \;\;\;\;\;\;\;\int_{{\theta _0}}^{{\rm{ \mathsf{ π} }} - {\theta _0}} {\int_0^{\alpha \left( {{\theta _0},{t_k}} \right)} {f\left( {{t_k},{r_k}} \right){\rm{d}}{r_k}{\rm{d}}{t_k}} } \\ \;\;\;\;\;\;\;\;\;\;\;{M_{\rm{P}}} = 2\\ \sum\limits_{j = 1}^J {2\left[ {\int_{{\theta _{1,ij}}}^{\rm{ \mathsf{ π} }} {\int_0^{\alpha \left( {{\theta _0},{\theta _{1,ij}}} \right)} {f\left( {{t_k},{r_k}} \right){\rm{d}}{r_k}{\rm{d}}{t_k}} } + } \right.} \\ \;\;\;\;\;\;\;\left. {\int_{{\theta _0}}^{{\theta _{1,ij}}} {\int_0^{\alpha \left( {{\theta _0},{t_k}} \right)} {f\left( {{t_k},{r_k}} \right){\rm{d}}{r_k}{\rm{d}}{t_k}} } } \right]\\ \;\;\;\;\;\;\;\;\;\;\;{M_{\rm{P}}} > 2 \end{array} \right. $ | (9) |
其中:θ0为相邻星座距离的一半,θ1, ij(j=1, 2, …, J)为接收星座点PR, k与其判决区域J个端点的距离,函数α(θ, t)为
| $ \alpha \left( {\theta ,t} \right) = 2\arccos \left( {\tan \theta /\tan t} \right) $ | (10) |
受高斯噪声影响,MQ阶QAM星座点引入的误符号率函数可表示为
| $ \begin{array}{l} {S_{{\rm{Q}},k}} = 2\left( {1 - \frac{1}{{\sqrt {{M_{\rm{Q}}}} }}} \right){\rm{erfc}}\left( {\sqrt {\frac{{3G}}{{{M_{\rm{Q}}} - 1}}} } \right) - \\ \;\;\;\;\;\;\;{\left( {1 - \frac{1}{{\sqrt {{M_{\rm{Q}}}} }}} \right)^2}{\rm{erf}}{{\rm{c}}^2}\left( {\sqrt {\frac{{3G}}{{{M_{\rm{Q}}} - 1}}} } \right) \end{array} $ | (11) |
在得到每个子载波误符号率函数的基础上,可以推导相应的频谱效率函数.下面采用有效数据速率Re与所占用带宽B的比值来衡量频谱效率,即η=Re/B.基于极化状态—幅度—相位调制,每个子载波可实现的Re为
| $ \begin{array}{*{20}{c}} {{R_{ek}} = {N_{{\rm{SQK}}}}\left( {1 - {S_{{\rm{Q}},k}}} \right){\rm{lb}}\left( {{M_{\rm{Q}}}} \right) + }\\ {{N_{{\rm{SPK}}}}\left( {1 - {S_{{\rm{P}},k}}} \right){\rm{lb}}\left( {{M_{\rm{P}}}} \right)} \end{array} $ | (12) |
结合GNURadio和USRP X300及水平—垂直正交双极化天线,本节分别测试了一定信噪比下Bob和Eve接收星座图的情况.
USRP X300采用Kintex-7 FPGA,支持2个宽频带射频子板通道,采用万兆以太网接口,射频子板采用SBX-120,支持400~4 400 MHz频率覆盖.选择天线型号为KBT65VH15-24RT0,频率范围为2 400~2 500 MHz,天线增益为(2×15±1)dBi,最大功率200 W.设置Alice和Bob相距25 m,Alice和Eve相距30 m.结合天线和USRP硬件参数,设置实验参数如表 1所示.
|
|
表 1 实验相关参数设置 |
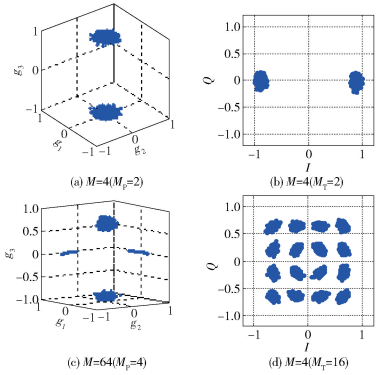
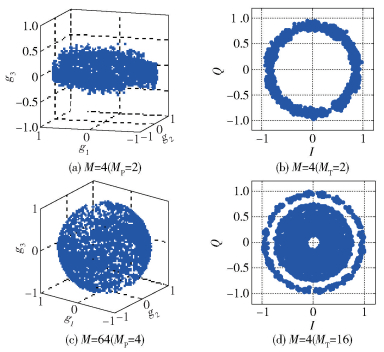
图 8和图 9分别为Bob和Eve在接收信噪比为22 dB时,恢复出的4MCM和64MCM信号的星座图情况.
|
图 8 Bob在信噪比为22 dB时恢复出的4MCM和16MCM的星座图 |
|
图 9 Eve在信噪比为22 dB时恢复出的4MCM和16MCM的星座图 |
从图 8和图 9可以看出,当信噪比为22 dB时,合法接收端能够很好地恢复出高维星座图,而窃听端接收到的星座图十分紊乱,无论是极化星座图还是传统调制对应的二维星座图,都是严重扰乱过的.即使信噪比很高,由于高维星座映射方案和信道预补偿的引入,窃听端仍然无法恢复出信号的有效信息.
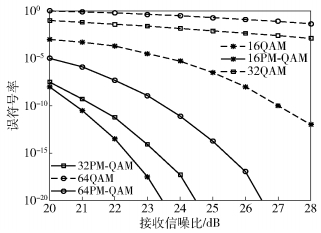
5.2 对系统误码性能的分析利用式(6),对极化多维星座图调制的误符号率及频谱进行相应的仿真,并与基于QAM的OFDM系统进行对比,所得结果如图 10和图 11所示.
|
图 10 OFDM极化多维星座调制与OFDM-QAM误符号率仿真对比 |
|
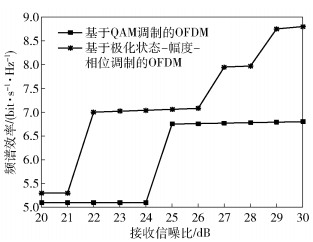
图 11 OFDM极化多维星座调制与OFDM-QAM频谱效率仿真对比 |
由图 10和图 11可以发现在相同信噪比下,所提极化状态—幅度—相位调制(PM-QAM)的误符号率及频谱效率都显著优于传统OFDM-QAM调制.
6 结束语笔者提出了利用极化状态调制实现加密OFDM移动通信系统物理层的理论与方法,设计了一种极化调制和QAM相结合的高维星座图,可以利用无线信道的去极化效应,实现调制信息的保护,使窃听者无法解调出信息.由于极化状态调制具有与已有的调制方式兼容性高、频谱利用率高、安全性高等特点,为解决无线链路开放性造成的移动通信信息安全隐患这一难题开辟了一条新的途径.
| [1] | Cao Jin, Ma Maode, Li Hui, et al. A survey on security aspects for LTE and LTE-A networks[J]. IEEE Communications Surveys and Tutorials, 2014, 16: 283–302. doi: 10.1109/SURV.2013.041513.00174 |
| [2] | Akitaya T, Asano S, Saba T. Time-domain artificial noise generation technique using time-domain and frrequency-domain processing[C]//ICC-2014 IEEE International Conference on Communication Workshop.[S. l]: IEEE, 2014: 807-812. |
| [3] | Li Xiaohua, Hwu J, Ratazzi E P. Using antenna array redundancy and channel diversity for secure wireless transmissions[J]. Journal of Communications, 2007, 2(3): 24–32. |
| [4] |
穆鹏程, 殷勤业, 王文杰. 无线通信中使用随机天线阵列的物理层安全传输方法[J]. 西安交通大学学报, 2010, 44(6): 62–66.
Mu Pengcheng, Yin Qinye, Wang Wenjie. Physical layer secure transmission method using random antenna arrays in wireless communication[J]. Journal of Xi'an Jiaotong University, 2010, 44(6): 62–66. doi: 10.3969/j.issn.1008-245X.2010.06.010 |
| [5] |
侯晓赟, 黄庭金, 朱艳, 等. 增强物理层安全的联合发射天线选择和人工噪声技术[J]. 信号处理, 2014(11): 1263–1266.
Hou Xiaoyun, Huang Tingjin, Zhu Yan, et al. Joint antenna selection and artificial noise enhancement for physical layer security[J]. Signal Processing, 2014(11): 1263–1266. doi: 10.3969/j.issn.1003-0530.2014.11.004 |
| [6] |
李明亮, 黄开枝, 朱晖. 基于时域参考的物理层安全传输方案[J]. 计算机应用研究, 2013, 30(12): 3738–3741.
Li Mingliang, Huang Kaizhi, Zhu Hui. Physical layer secure transmission scheme based on time domain reference[J]. Application Research of Computers, 2013, 30(12): 3738–3741. doi: 10.3969/j.issn.1001-3695.2013.12.057 |
| [7] |
冯干青, 何海浪. OFDM同步技术研究[J]. 数字技术与应用, 2014(5): 122–122.
Feng Ganqing, He Hailang. OFDM synchronization technology research[J]. Journal of Digital Technology and Applications, 2014(5): 122–122. |
| [8] | Benedetto S, Poggiolini P. Theory of polarization shift keying modulation[J]. IEEE Transactions on Communications, 1992, 40(4): 708–721. doi: 10.1109/26.141426 |
| [9] | Bulow H. Polarization QAM modulation (POL-QAM) for coherent detection schemes[C]//Conference on Optical Fiber Communication.[S. l]: IEEE, 2009: 1-3. |
| [10] | Wei D, Liang L, Zhang M, et al. A polarization state modulation based physical layer security scheme for wireless communications[C]//Military Communications Conference, Milcom 2016.[S. l.]: IEEE, 2016: 1195-1201. |
| [11] | Luo Z, Wang H, Hao H. A spectrum efficient spatial polarized QAM modulation scheme for physical layer security in dual-polarized satellite systems[J]. IEICE Transactions on Communications, 2018, 101(1): 146–153. |
| [12] | Zhang J, Wang Y, Zhang J, et al. Polarization shift keying (PolarSK):system scheme and performance analysis[J]. IEEE Transactions on Vehicular Technology, 2017(PP99): 1–1. |


