2. 南阳师范学院 计算机与信息技术学院, 河南 南阳 473061
针对联合采用超时机制和通配符匹配机制的规则放置问题,提出了基于时空联合的规则放置算法TSRPM,综合考虑了规则在流表中的逗留时间和规则的匹配空间,以确定规则的放置方案.实验结果表明,所提算法产生的规则放置方案能够有效提高规则命中率,降低分组拒绝率.
2. School of Computer and Information Technology, Nanyang Normal University, Henan Nanyang 473061, China
Time-space based rules placement method (TSRPM) is proposed for solving the problem of rules placement utilizing both timeout and wildcard match schemes. The sojourn time and space of a rule are both considered to decide rules placement approach in TSRPM. The results of simulation show that TSRPM can improve the match rate and reduce the packet refused rate.
OpenFlow提供的超时机制和通配符匹配机制可以有效解决流表空间不足的问题[1].但是,通配符的引入使得不同规则覆盖的数据流范围可能会相互重叠,产生规则依赖关系[2-3].为了保证语义的正确性,当控制器收到对应于任意规则的请求消息时,该规则的所有依赖规则也必须下发.对于每条规则覆盖的数据流空间,平均与其他数十条规则覆盖的数据流空间重叠[4],并且由于OpenFlow规则包含多个匹配域,每条规则的依赖规则会呈现雪崩式增长. CMR(Caching micro-rules)算法[5]将全部规则分解成相互独立的规则,彻底地消除了规则间的依赖关系.但是,由于平均每条规则都有数十条依赖规则[4],所以CMR会导致分解后的规则数量急剧增加. CAB(CAching in Buckets)算法[4]有效限制了规则依赖链长度的增加,但是CAB算法需要多级流表的支持.
OpenFlow规则包含硬超时时间和空闲超时时间.现有的控制器将硬超时时间和空闲超时时间设为固定值[6-7]. Liang Haochi等[8]建立了硬超时时间与数据流中断次数和阻塞分组之间的数学模型,但模型建立在数据流的到达过程服从泊松分布的基础上,适用范围具有一定的局限性. TimeoutX[9]提供了根据数据流特征设置规则空闲超时的方法,提高了分组的命中率和流表的有效利用率,但需要控制器对数据流进行监测,增加了通信开销.
所提出的基于时空联合的规则放置算法根据流表空闲空间设置规则的空闲超时时间,不需要对数据流进行监测,在保持原有设备不变的情况下,通过评估通配规则的存储开销灵活选择精确匹配规则或者通配规则,进一步减少流表资源浪费.
1 问题描述首先给出规则依赖和规则匹配的相关定义,然后对在流表空间和规则依赖约束下的规则放置问题进行形式化描述.
定义1 如果匹配域M0中任意匹配项mi0是M1中对应匹配项mi1的子集,并且存在匹配项mj0是匹配项mj1的真子集,那么M0是M1的真子集,记为M0⊂M1.其中mxy表示匹配域Mx的第y个匹配项.
定义2 假设规则ri(i∈{0, 1})的匹配域为Mi,优先级为prii,并且pri0 < pri1,如果存在匹配域M3使得M3⊂M0∪M3⊂M1成立,那么r1是r0的依赖规则.
定义3 在原始规则集中,ri的所有依赖规则构成的集合称为ri的依赖规则集,记作Di.
假设时刻t到达交换机的分组为pt,如果交换机中不存在与分组pt对应的规则,则交换机向控制器发送规则请求消息(即packet-in).控制器收到规则请求消息后,根据特定规则放置算法生成规则集ℜt. ℜt中可能包含1个或者多个规则.例如,采用精确规则下发方式的规则放置算法直接根据pt的包头和相应决策构造精确规则进行下发,采用基于依赖规则下发方式的规则放置算法将pt匹配的原始规则及其所有依赖规则进行下发.如果交换机中的剩余流表空间不小于|ℜt|,则控制器下发规则集ℜt,否则拒绝分组pt的规则请求.设xt表示分组pt在交换机中是否命中规则,则
| $ {x_t} = \left\{ \begin{array}{l} 1, \;\;如果{p_t}成功命中规则\\ 0, \;\;其它情况 \end{array} \right. $ | (1) |
设yt表示控制器是否可以分组pt分配规则,则
| $ {y_t} = \left\{ \begin{array}{l} 1, \;\;如果{p_t}的规则请求被拒绝\\ 0, \;\;其它情况 \end{array} \right. $ | (2) |
假设一个SDN交换机的流表空间大小为C,时刻t∈T流表中的规则集合为Rt,任意规则ri∈Rt的匹配集为Mi,优先级为gi,指令集为Ai,硬超时时间为hi,空闲超时时间为ui,安装时间为ai,截止到时刻t,最近被命中的时刻为lt, i.根据上述定义,规则放置问题形式化描述如下:
| $ \begin{array}{c} \min \sum\limits_{t \in T} {\alpha (1 - {x_t})} + \left( {1 - \alpha } \right){\rm{ }}{y_t}\\ {\rm{s}}{\rm{.t}}{\rm{.}}~~|{R_t}| \le C, \forall t \in T \end{array} $ | (3) |
| $ {D_r} \subseteq {R_t}, \forall t \in T, \forall r \in {R_t} $ | (4) |
| $ t - {l_{t, i}} < {u_i}, \forall t \in T, \forall {r_i} \in {R_t} $ | (5) |
| $ t - {a_i} < {h_i}, \forall t \in T, \forall {r_i} \in {R_t} $ | (6) |
| $ {x_t}, {y_t} \in \left\{ {0, 1} \right\} $ | (7) |
规则放置问题的目标是设置合理的规则集ℜt,包括规则集中规则的数量,以及规则集任意规则的匹配集,优先级,硬超时时间和空闲超时时间,使得规则匹配失败的分组数量与被拒绝的分组数量的加权和最小.规则匹配失败使得交换机需要向控制器申请规则,从而增加分组时延;分组被拒绝使得相关用户无法访问网络.规则匹配失败率和分组拒绝率之间存在权衡问题,因此设置权重α用于根据不同网络需求确定规则匹配失败的分组数量与被拒绝的分组数量的偏好.约束条件式(3)表示任意时刻流表中规则的数量都不能超过流表的最大容量.约束条件式(4)表示任意时刻,任意规则都不能脱离它的依赖规则单独存在于流表中.约束条件式(5)表示任意时刻,流表中不存在空闲超时的规则.约束条件式(6)表示任意时刻,流表中不存在硬超时的规则.
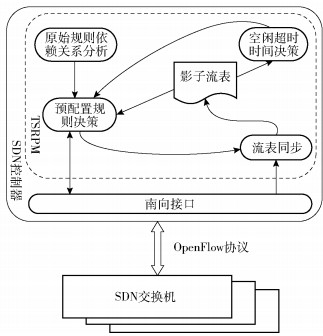
2 基于时空联合的规则放置方法基于时空联合的规则放置方法(TSRPM, time-space based rule placement method)可以作为一个应用运行于控制器上.如图 1所示,TSPRM包含原始规则依赖关系分析,空闲超时时间决策,预配置规则决策,影子流表和流表同步5个模块.原始规则依赖关系分析模块负责根据上层网络管理策略(路由、防火墙、访问控制)等生成的规则构建规则依赖树;预配置规则模块是TSRPM的核心,根据当前流表状态,规则请求消息和规则依赖树决策下发的规则集,在决策过程中适时调用空闲超时时间决策模块;影子流表模拟交换机的流表,存储的规则始终与流表保持一致,为预配置规则决策模块和空闲超时时间决策模块提供依据,由流表同步模块适时更新.接下来对分别对原始规则依赖关系分析模块、空闲超时决策模块和预配置规则决策模块进行详细描述.
|
图 1 TSRPM算法功能模块 |
高层管理策略通过编程语言转换为带有通配符的粗粒度规则,在本文中这些规则称为原始规则.原始规则间的依赖关系可以用邻接表表示.依赖邻接表的每个头节点包含3个域:当前规则的编号、当前规则的直接(全部)依赖规则数量、当前规则的直接(全部)依赖规则链表的头指针.每个表节点包含2个域:当前依赖规则的编号、指向下一个表节点的指针.依赖邻接表的构建过程可以分为2个阶段,首先根据定义3找到每个规则的依赖规则集,建立直接规则依赖邻接表,然后迭代查找并添加每个依赖规则的依赖规则,建立全部规则依赖邻接表.
2.2 空闲超时时间决策如何选择空闲超时时间是一个均衡问题.一方面,如果规则的空闲超时时间过大,那么规则在流表中逗留的时间会比较长,导致流表被快速耗尽,到达时间较晚的数据流被拒绝;另一方面,如果规则的空闲超时时间过小,会增加当前数据流向控制器请求规则的次数.
采用流表状态感知的空闲超时时间设置机制:1)当流表空闲空间比较充足时,为了减少当前规则被请求的次数,为当前规则设置较大的空闲超时时间,2)当流表空闲空间有限时,为了避免或推迟之后到达的数据流被拒绝,为当前规则设置较小的空闲超时时间.空闲时时时间具体的计算公式为
| $ u = \max (\gamma , \beta (1 - {R_t}/C)) $ | (8) |
其中:β>0,用于调整空闲超时时间的变化幅度.显然,在β确定的情况下空闲超时时间与空闲空间大小成正比.由于Rt/C < 1,所以空闲超时时间的上限为β.为了避免空闲超时时间过小,设置参数γ,本文设γ为1 ms.
2.3 预配置规则决策预配置规则决策过程如算法1所示,查找分组pt命中的原始规则originalRule(第1行),调用原始规则依赖关系分析模块获取originalRule的依赖规则的集合dependencyRS(第2行),查找影子流表中被originalRule及其依赖规则覆盖的精确规则的集合exactRS(第3行),调用空闲超时时间决策模块计算空闲超时时间idleTimeout(第4行),接下来根据exactRS和dependencyRS中规则的数量构建预配置规则ℜt,分为3种情况.
情况1(第5~7行): dependencyRS中规则的数量大于exactRS中规则的数量或者剩余流表不能容纳dependencyRS中的规则,直接根据pt的报头构建精确规则,规则的优先级设为默认优先级,空闲超时时间设为idleTimeout,硬超时优先级设为最大值.
情况2(第8~10行): dependencyRS为空,即originalRule独立于其它规则,将originalRule作为预配置规则,将其规则的优先级设为默认优先级,空闲超时时间设为idleTimeout,硬超时时间设为最大值.
情况3(第11~20行): dependencyRS不为空,但是dependencyRS中规则的数量小于exactRS中规则的数量并且剩余流表能够容纳dependencyRS中的规则,首先查询exactRS中所有规则的优先级的最大值maxPriority,然后设置依据originalRule构建新规则,新规则的优先级大于maxPriority,使得当新规则放置到交换机之后,该规则覆盖的所有精确匹配规则尽快失效,释放流表空间,新规则的空闲超时时间设为idleTimeout,硬超时优先级设为最大值maxHardT.为了避免语义错误,originalRule的所有依赖规则也必须被放置到交换机中,以新规则的优先级为基础设置每个依赖规则的优先级,保持每个依赖规则的优先级与originalRule的差值与它们在原始规则集中的差值一致.为了保证依赖规则被从流表中清除的时间不早于originalRule,设置所有依赖规则的空闲超时时间为最大值maxIdleT.
算法1 预配置规则决策算法
输入:pt,C,γ,β,maxIdleT,maxHardT,defaultHardT,defaultPriority
输出:ℜt
1 originalRule←lookupOriginalRule(pt)
2 dependencyRS←dependencyAnalyzer(originalRule)
3 exactRS←lookupShadowTable(dependecyRS)
4 u←idleTimeoutGenerator (β, Rt, C, γ)
5 if |dependecyRS|>|exactRS|
6 or freeTableSize < |dependencyRS| then
7 rule←creatRule(pt, defaultPriority, u, maxHardT)
8 addRule(rule, ℜt)
9 else if dependecyRS is NULL then
10 rule←creatRule(originRule, defaultPriority, u, maxHardT)
11 addRule(rule, ℜt)
12 else
13 maxPriority←getMaxPriority(exactRS)
14 priority←setPriority(maxPriority, originRule)
15 rule←creatRule(originRule, priority, u, defaultHardT)
16 addRule(rule, ℜt)
17 for all dependencyRule in dependencyRS
18 priority←setPriority(maxPriority, originRule, dependencyRule)
19 rule←creatRule(dependencyRule, priority, maxIdleT, defaultHardT)
20 addRule(rule, ℜt)
21 end for
22 end if
23 shadowTableSyn(ℜt)
24 return ℜt
3 仿真与性能分析 3.1 仿真实验设计在多种流表空间大小下对比TSRPM与其它规则放置算法的性能.实验所用的规则集和数据流利用ClassBench[10]根据公开数据源进行合成.
利用c++实现了一个SDN模拟器,用于评估TSRPM及其对比算法的性能.本文采用的对比算法如下:
1) 基于精确匹配和空闲超时时间固定的规则放置算法(EMFIT, exact match and fix idle timeout-based rules placement):对于每个规则请求,算法生成精确匹配规则,所有规则的空闲超时时间相同.
2) 基于精确匹配和硬超时时间固定的规则放置算法(EMFHT, exact match and fix hard timeout-based rules placement):对于每个规则请求,算法生成精确匹配规则,所有规则的硬超时时间相同.
3) 基于规则依赖和硬超时时间固定的规则放置算法(RDFHT, rules dependency and fix hard timeout-based rules placement):对于每个规则请求,算法下发请求命中的原始规则及其所有依赖规则,所有规则的硬超时时间相同.
4) 基于精确匹配和动态空闲超时时间机制的规则放置算法(EMAIT, Exact Match and Adaptive Idle Timeout-based rules placement):对于每个规则请求,算法生成精确匹配规则,所有规则的空闲超时时间根据当前可用的流表空间大小确定,计算方式如式8所示.
评价指标为分组拒绝率(PRR, packet refused rate)和分组规则匹配失败率(PMR, packet missed rate).它们的计算方式如下:
PRR=申请规则失败的分组数量/总的分组数量,PMR=规则匹配失败的分组数量/总的分组数量.
在获取真实数据集比较困难的情况下,ClassBench是常用的合成近似真实规则集和数据流的工具[4, 11]. ClassBench还提供了一些用于生成规则集的种子文件,包括访问控制列表(ACL, access control list),IP链(IPC, IP Chain)和防火墙(FW, firewall).利用ClassBench的db_generator和trace_generator组件生成的规则,数据流和分组数量如表 1所示,选用的种子文件分别是acl1_seed,ipc1_seed,fw1_seed.
|
|
表 1 实验数据集 |
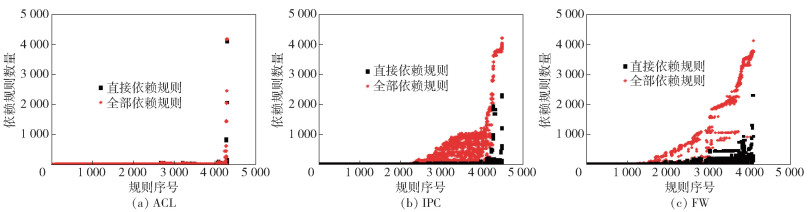
图 2所示为采用TSRPM中的原始规则分析模块得出的各组数据源中原始规则的依赖情况.每组数据源中的规则按优先级由高到低进行排列.观察发现:规则的优先级越低,它的依赖规则越多;每个规则全部依赖规则的数量至多高出其直接依赖规则数量多个数量级;ACL、IPC和FW三个原始规则集中的平均依赖规则数量依次增多.
|
图 2 规则依赖 |
实验分别在9种不同场景下进行.不同场景使用的流表空间(500,1 000或者2 000)或者数据源(ACL、IPC或者FW)不同.在每种场景下,通过将EMFIT中的空闲超时时间,EMFHT和RDFHT中的硬超时时间以及EMAIT中的β设置为{0.2 s, 0.4 s, 0.6 s, …, 20 s},使得每种算法分别得到100组.为了便于描述,如果对于算法A得到的任意结果,在算法B得到的结果中至少存在一种帕累托改进,而对于算法B得到的任意结果,在算法A得到的结果中不存在帕累托改进,那么称算法B优于算法A.显然,如果算法B优于算法A,那么无论权重α为何值,采用算法B总能得到一种结果,使得目标函数的值更小.也就是说在保障网络承载相同数量的数据流的情况下,采用RDFHT得到的规则放置方案可以较高的分组命中率,减少数据流的时延;另一方面在保障相同分组命中率的情况下,采用RDFHT可以使网络承载较多的数据流.
|
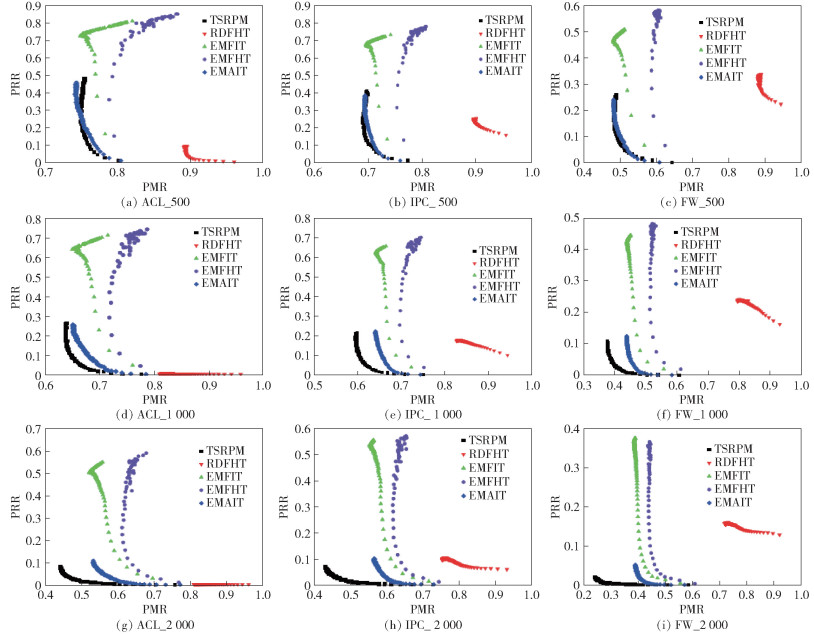
图 3 算法性能对比PRR和PMR |
图 3给出各算法不同场景下得到的放置方案对应的PRR和PMR.可以发现,同一流表空间下,RDFHT对于ACL规则集得到的结果最优,对于IPC规则集次之,对于FW规则集最差.例如,对比图 3(a)~(c)可以发现,在流表空间为500时RDFHT对于ACL规则集得到的结果优于IPC和FW规则集,并且对于IPC规则集的结果优于FW规则集.原因是这3种规则集中平均每个规则的依赖规则数量依次升高.
对于任意流表空间大小和任意规则集,采用TSRPM和EMAIT得到的解集总是优于RDFHT,EMFIT和EMFHT.在流表空间较大时,TSRPM优于EMAIT.如图 3(e)所示,在流表空间为1 000时,对于IPC规则集,TSRPM得到的解集优于EMAIT,RDFHT,EMFIT和EMFHT,并且EMAIT又优于其余3种算法.在TSRPM得到的结果中,PMR是PRR的单调递减函数,不能使得PMR和PRR同时达到最优,但是可以根据偏好通过调整β的值,获得理想的PMR或者PRR.
4 结束语OpenFlow的超时机制和通配符匹配机制分别从时间和空间方面约束了规则对流表空间的占用.因此,通过合理设置规则的超时时间和匹配项可以提高流表的利用率.笔者首先对联合采用超时机制和通配符匹配机制的规则放置问题进行形式化描述,然后提出了基于时空联合的规则放置方法TSRPM. TSRPM首先求解规则之间的依赖关系,然后根据当前流表的使用情况及当前规则请求消息对应的原始规则所依赖的规则数量,决策合理的下发规则集及规则集中各规则的超时时间.实验结果表明,相对于EMFIT、EMFHT、RDFHT和EMAIT,TSRPM产生的规则放置方案能够有效提高规则命中率,降低分组拒绝率.
| [1] | Nguyen X N, Saucez D, Barakat C, et al. Rules placement problem in openflow networks:a survey[J]. IEEE Communication Survey and Tutorials, 2016, 18(2): 1273–1286. doi: 10.1109/COMST.2015.2506984 |
| [2] | Katta, Naga, Omid Alipourfard, Jennifer Rexford, et al. Infinite cacheflow in software-defined networks[C]//2014 ACM the third workshop on Hot topics in software defined networking. New York: ACM Press, 2014: 175-180. Infinite cacheflow in software-defined networks |
| [3] | Zhang Shuyuan, Franjo Ivancic, Cristian Lumezanu, et al. An adaptable rule placement for software-defined networks[C]//2014 IEEE/IFIP Dependable Systems and Networks (DSN). New York: IEEE Press, 2014: 88-99. http://ieeexplore.ieee.org/document/6903570/ |
| [4] | Yan B, Xu Y, Xing H, et al. CAB: a reactive wildcard rule caching system for software-defined networks[C]//2014 ACM Third Workshop on Hot Topics in Software Defined Networking. New York: ACM, 2014: 163-168. |
| [5] | Dong Q, Banerjee S, Wang J, et al. Wire speed packet classification without tcams:a few more registers (and a bit of logic) are enough[J]. SIGMETRICS Perform, 2007, 35(1): 253–264. doi: 10.1145/1269899 |
| [6] | Iyer A S, Mann V, Samineni N R. Switch reduce: reducing switch state and controller involvement in openflow networks[C]//2013 IFIP Networking Conference. Piscataway: IEEE, 2013: 1-9. |
| [7] | Curtis A R, Mogul Jeffrey C, Tourrilhes J, et al. DevoFlow:scaling flow management for high performance networks[J]. SIGCOMM Comput Commun Rev, 2011, 41(4): 254–265. doi: 10.1145/2043164 |
| [8] | Zhang L, Lin R, Xu S, et al. AHTM: achieving efficient flow table utilization in software defined networks[C]//2014 IEEE Global Communications Conference. Piscataway: IEEE, 2014: 1897-1902. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7037085 |
| [9] | Zhang L, Wang S, Xu S, et al. TimeoutX: an adaptive flow table management method in software defined networks[C]//2015 IEEE Global Communications Conference (GLOBECOM). Piscataway: IEEE, 2015: 1-6. |
| [10] | Taylor David E, Turner Jonathan S. ClassBench:a packet classification benchmark[J]. IEEE/ACM Transactions on Networking (TON), 2007, 15(3): 499–511. doi: 10.1109/TNET.2007.893156 |


