针对无线传感器网络(WSN)中数据计算需求和由簇首负载过重引起的热点问题和能量空洞问题,提出基于计算节点和转发节点的自组织聚簇算法(SCATN),对簇首功能进行分解,以计算节点满足数据计算需求,以转发节点进行数据转发,并通过分布控制解决热点问题和能量空洞问题.聚簇过程采用自组织方式控制功能节点的生成、分布,从而解决分布不均匀和连接性问题.同时,普通节点自主更换归属簇以及时、细粒度地调整计算节点负载.仿真实验结果表明,与现有几种聚簇算法相比,SCATN算法可有效地提高网络生存时间,增加基站的吞吐量,降低丢包率.
A self-organized clustering algorithm based on computation node and transmission node (SCATN) for wireless sensor network (WSN) was proposed to satisfy computation requirement and solve the problem of hot spot and energy hole caused by cluster head overload. SCATN employs computation node and transmission node to undertake the cluster head's function data computation and transmission. The distribution probability of functional nodes is controlled to tackle with the problems raised. The generation and distribution of functional node is controlled by self-organized manner to solve the problem of distribution and connection. The ordinary nodes choose its belonged cluster to adjust the computation node's load. Simulation indicates that SCATN can effectively extend the network lifetime, improve the throughput at the sink and decrease the packet loss rate in comparison with several existing clustering algorithms.
随着物联网(IoT, internet of things)和大数据的快速发展,感知数据已从简单的温湿度数据发展到视频等多媒体内容,且感知数据量庞大,超出无线传感器网络(WSN, wireless sensor network)的传输能力,将大量数据传输到一个中心进行处理,从技术上和经济上都是不现实的.现在的传感器节点有较强的计算和存储能力,可以在网络中进行数据处理[1].现有聚簇方法通常采用双簇首(CH, cluster head)的方法解决热点问题,采用非均匀聚簇的方法解决能量空洞问题,并假设CH的数据处理任务简单,不能满足数据计算的需求.张人上等[2]和刘壮等[3]采用双CH的方法,2个CH分别负责簇内数据收集、处理和簇间数据转发.戴志强等[4]对规模较大的簇选取副CH以减少CH的负担. Mo等[5]采用非均匀聚簇的方法,根据到sink的距离确定每环的CH数目,使靠近sink的环有更多的CH. Afsar等[6]使靠近sink的CH之间距离更小,从而实现非均匀聚簇. Vural等[7]提出了异步聚簇协议(ACP, asynchronous clustering protocol),根据各环的流量负载计算各环的CH基准概率,根据基准概率计算簇范围,使靠近sink的环内节点的CH基准概率大,簇范围小,从而实现非均匀聚簇.吴标等[8]计算了不同网络区域的CH比例,通过CH发射功率的自适应调整实现非均匀聚簇.非均匀聚簇算法虽然能够获得CH能耗的近似相等,但是由于靠近sink的网络区域CH节点较多,增加了该区域的总体能耗,从而不能很好地解决能量空洞问题.此外,IoT和大数据需要CH进行数据计算、网络管理和数据转发等任务,因此需要稳定的网络拓扑.传统的双CH算法和非均匀聚簇算法不能满足数据计算需求,没有考虑计算节点的分布和双CH的相互影响.
针对上述问题,笔者提出基于计算节点和转发节点的自组织聚簇算法(SCATN, self-organized clustering algorithm based on computation node and transmission node).该聚簇算法将CH功能分解到相互独立的计算节点(CCH, computation function of cluster head)和转发节点(TCH, transmission function of cluster head),根据数据计算需求确定CCH的分布,根据数据转发需求确定TCH的分布,并通过综合控制CCH和TCH的分布关系以缓解能量空洞问题. SCATN在算法运行过程进行存在性和连接性检查从而确保TCH的连接性,并且通过普通节点自主更换归属簇及时调整CCH的负载.
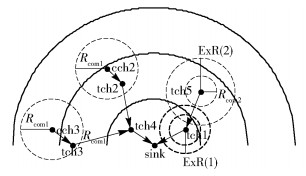
1 系统模型 1.1 网络模型网络模型如图 1所示.大规模WSN中,网络会形成以sink为中心的等宽环形区域,环内节点到sink有相同的跳数[9].节点可调整自己的传输功率,从而覆盖不同的通信范围[6-7]. SCATN算法中节点有3个固定的通信范围Rcom1、Rcom2和ExR(h)(其中h为节点的跳数).网络中节点角色分为普通节点、CCH和TCH.普通节点进行数据感知,并在范围Rcom1内相互交换电量信息,以获得局部范围的最大电量,用于CCH的选举. CCH负责簇内节点的数据收集和处理,转发数据到TCH,通信范围为Rcom1,如图 1中cch2和cch3的簇范围,与tch2、tch3的转发数据范围均为Rcom1. TCH负责转发数据到sink,转发范围为Rcom1,如图 1中tch2与tch3转发数据到tch4,tch4转发数据到sink.为使TCH有较好的分布,每个TCH节点在范围ExR(h)内进行存在性和连接性检查,并且在较小的附近范围Rcom2内进行角色的更换,如图 1中tch5的附近范围为ExR(1),tch5存在范围为ExR(2),跳数不同存在范围不同.
|
图 1 网络模型 |
Vural等[7]采用环形能量计算方法分析CH负载,忽略了CH的数据收集、计算负载,因而不太准确. TCH的负载仅为数据转发负载,所以使用环形能量计算方法更加准确.
定义1[7] 跳数是h的环内节点成为TCH的基准概率为tbenp(h)(见式(1)),成为TCH的概率为PTCH(i).
| $ {t_{{\rm{benp}}}}\left( h \right) = \frac{{{K^2} - {h^2} + 2h - 1}}{{\left( {2h - 1} \right){K^2}}}{t_{{\rm{benp}}}}\left( 1 \right) $ | (1) |
| $ {t_{{\rm{benp}}}}\left( 1 \right) = \frac{M}{{C\sigma {\rm{ \mathsf{ π} }}{R^2}}} $ | (2) |
其中:K为网络的最大跳数,M为网络中初始TCH数目,
Vural等[7]中对网络进行流量分析,使各环CH转发的数据流量相等,从而求出各环所需的CH数量,并进一步确定各环CH的基准概率.考虑节点的电量和TCH基准概率,PTCH(i)的计算公式为
| $ {P_{{\rm{TCH}}}}\left( i \right) = {t_{{\rm{benp}}}}({\rm{hop}}\left( i \right))\frac{{E\left( i \right)}}{{{\varepsilon _{{\rm{max}}}}\left( i \right)}} $ | (3) |
其中:hop(i)为节点i的跳数,E(i)为节点i的电量,εmax(i)为节点i邻居范围内节点的最大电量.
定义2 定义ExR(h)为跳数是h的环内TCH的存在范围,不同环的存在范围不同.节点通过其TCH列表检查在其该范围内是否有TCH存在,如果没有就会启动TCH选举过程,如果有则不会生成新的TCH,从而对TCH的拓扑进行控制.由于各环的TCH分布随机且互不影响,所以各环TCH的分布符合泊松分布,该范围内TCH节点的平均个数λ为σπExR2(h)tbenp(h).由
| $ {\rm{ExR}}\left( h \right) \approx \sqrt {\frac{{2\ln 10}}{{\sigma {\rm{ \mathsf{ π} }}{t_{{\rm{benp}}}}\left( h \right)}}} $ | (4) |
计算节点CCH的分布需求具有以下3个特点:①远离sink的区域存在更多的传感器节点,所以需要更多的计算节点;②在远离sink的区域进行数据计算,可以减少网络中传输的数据量;③在靠近sink的网络区域分布较少的CCH,以减少该网络区域的能耗,从而均衡整个网络的负载.
定义3 定义cbenp(h)为跳数是h的环内节点成为CCH的基准概率,成为CCH的概率为PCCH(i).以h1和h2代表任意2个不同环的跳数,以a1、a2为对应环的面积,为实现整个网络的负载均衡,使各环的高能耗节点TCH与CCH的数目之和与环中节点的总数目成比例,即
| $ \frac{{{a_1}\sigma ({t_{{\rm{benp}}}}({h_1}) + {c_{{\rm{benp}}}}({h_1}))}}{{{a_2}\sigma ({t_{{\rm{benp}}}}({h_2}) + {c_{{\rm{benp}}}}({h_2}))}} = \frac{{{a_1}\sigma }}{{{a_2}\sigma }} $ |
得到tbenp(h1)+cbenp(h1)=tbenp(h2)+cbenp(h2).由于0 < tbenp(h), cbenp(h) < 1,所以可以设各环节点的2种基准概率之和为1,得到
| $ {c_{{\rm{benp}}}}\left( h \right) = 1 - {t_{{\rm{benp}}}}\left( h \right) $ | (5) |
考虑节点的电量和CCH基准概率,PCCH(i)的计算公式如下:
| $ {P_{{\rm{CCH}}}}\left( i \right) = {c_{{\rm{benp}}}}({\rm{hop}}\left( i \right))\frac{{E\left( i \right)}}{{{\varepsilon _{{\rm{max}}}}\left( i \right)}} $ | (6) |
定义4 定义Ceff(i)为CCH节点i的影响力. Ceff(i)的计算考虑以下3个因素:①节点i的电量;②节点i的基准概率;③节点i的簇内成员节点数目.普通节点根据CCH节点的影响力自主更换归属簇,可使同环CCH的负载均衡,远离sink的环CCH有更多的簇内节点. CCH从hello消息中获得簇内节点的电量和数目信息,Ceff(i)为
| $ {C_{{\rm{eff}}}}\left( i \right) = \frac{{E\left( i \right){c_{{\rm{benp}}}}({\rm{hop}}\left( i \right))}}{{{\rm{num}}\left( i \right)}} $ | (7) |
其中num(i)为CCH节点i的簇内成员节点数目.
2 SCATN算法 2.1 TCH、CCH选择网络中数据转发负载较大,所以首先进行TCH的选择. TCH的选择根据自组织群体中个体行为原则进行连接性和存在性检查,从而保证TCH有较好的分布和连接. TCH选择完成后,进行CCH的选择. TCH和CCH选择的流程如图 2所示.

|
图 2 TCH、CCH选择流程 |
算法步骤如下.
步骤1 根据式(1)和式(2)计算节点的TCH基准概率,进而根据式(4)和式(5)分别计算TCH存在范围和节点的CCH基准概率.
步骤2 跳数为0的sink节点在Rcom1范围内周期性广播tch_signal消息,普通节点在Rcom1范围内周期性广播hello消息,在Rcom2范围内周期性广播onForTCH消息. hello消息中包含节点的电量信息,节点收到hello消息后,计算其邻居范围内节点的最大电量,并根据式(3)和式(6)计算节点的TCH和CCH概率.
步骤3 节点设置其TCH定时器为(1-PTCH(i))T,设置其CCH定时器为(1-PCCH(i))T,并设置其初始间隔定时器为T.
步骤4 节点启动其TCH定时器和初始间隔定时器.当TCH定时器到期后,检查其tchExList确定TCH存在范围内是否有TCH存在,如果没有,检查其tchList列表内是否有可用TCH存在,如果有,则该节点成为TCH,关闭其初始间隔定时器,不再参与CCH的选择.并且,在Rcom1范围内周期性发送tch_signal消息,在其存在范围内广播一次tch_add消息.节点收到tch_signal消息后更新其tchList列表.节点收到tch_add消息后,如果跳数相同,则更新其tchExList列表,并停止TCH定时器.
步骤5 节点的初始间隔定时器到期后,启动其CCH定时器. CCH定时器到期后,成为CCH,在其簇范围Rcom1内发送一次cch_add消息,并周期性发送tch_signal消息.普通节点收到cch_add消息后,如果其CCH定时器没有到期,则停止其CCH定时器.
图 1中,sink发送tch_signal消息,sink跳数为0,所以跳数为1的节点更新其tchList,不会更新tchExList. tch1所代表节点的TCH定时器到期后,检查其tchExList和tchList,若满足条件,则可以成为TCH,然后发送tch_signal消息,跳数为1且在ExR(1)范围内的节点收到该消息后更新tchExList并关闭TCH定时器,不会再成为TCH,跳数为2且在ExR(2)范围内的节点收到该消息后会更新其tchList.因为所有节点的TCH定时器时间都小于初始间隔定时器,所以初始间隔定时器到期后,TCH选择结束开始CCH选择,cch2所代表节点的CCH定时器到期后,成为cch2,并在簇范围Rcom1内发送cch_signal消息,收到该消息的普通节点关闭CCH定时器并加入cch1.
2.2 TCH、CCH角色更换所提出的聚簇算法适用于大规模WSN,节点根据自身及局部范围内动态变化的节点和网络拓扑信息,做出适应性调整. CCH考虑电量和CCH基准概率信息进行角色更换,使电量较大、远离sink的节点能够优先成为CCH,同时要保证新的CCH节点到TCH的连接性. CCH节点j收到簇内节点i的hello消息后判断,如果j的tchList不为空,且E(j)cbenp(hop(j))>θ1E(i)cbenp(hop(i))(θ1为CCH角色更换阈值),则节点j代替i成为CCH.
TCH作为转发节点,为了保证路由的连续性,在附近范围Rcom2内进行角色更换,以维护路由拓扑的稳定性. TCH节点i收到邻居范围内同环节点j的onForTCH消息后判断,如果j的tchList不为空,且E(j)>θ2E(i)(θ2为TCH角色更换阈值),则节点j代替i成为TCH.
2.3 节点更换归属簇CCH通过cch_signal广播其影响力,普通节点收到该消息后,自主判断是否更换归属簇,从而在簇结构不发生大的变化的情况下对CCH的负载进行及时和细微的调整.
普通节点i,其当前归属簇为k,收到CCH节点j的cch_signal消息后判断,如果满足Ceff(j)>θ3Ceff(k)(θ3为归属簇更换阈值),则节点i更换其归属簇为j.
3 仿真结果及分析使用Matlab对算法进行仿真,在400 m×400 m的区域中随机地部署1 000个节点,sink位于网络区域的中心.节点的初始电量在1~2 J内随机分布.在数据处理能耗从5×10-9 J/bit~200×10-9 J/bit的多组实验中,TCH的平均数目为51,占节点总数的0.051%,TCH仅作为转发节点,会减少监测感知的节点数,但在大规模网络中,TCH节点数目较少且分布均匀,节点TCH角色转换后会重新开始监测,所以对网络的影响较少.
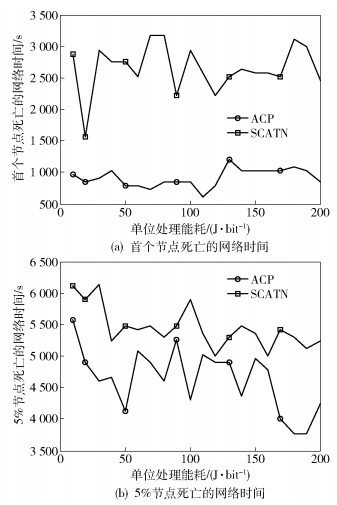
网络生存时间用首个节点和5%节点的死亡时间表示. ACP和SCATN的首个节点死亡的网络时间对比如图 3(a)所示.从图中可以看出,SCATN的网络时间比ACP有显著提高,通过20组实验的统计,ACP的网络时间平均值为907 s,SCATN的网络时间平均值为2 658 s. 5%节点死亡的网络时间对比如图 3(b)所示.从图中可以看出,SCATN的效果比ACP好,这是因为ACP中CH既承担数据转发,又进行计算,所以负载较重,网络生存时间较短. SCATN的平均时间是5 452 s,ACP的平均时间是4 636 s,二者差距比首个节点死亡的网络时间差距小,这是因为SCATN进行了拓扑控制,在不满足存在性和连接性条件的时候不进行TCH角色转换,会造成TCH节点死亡,而ACP中CH在电量较低时可以随时进行角色转换,不会导致节点直接死亡.由于低功耗自适应聚簇分层型协议(LEACH, low energy adaptive clustering hierarchy)中CH数据单跳传输到sink,所以在首轮就会出现节点死亡,网络生存时间较短.而不均匀聚簇路由算法(UCR, unequal cluster-based routing)在设置数据传输距离与ACP、SCATN相同时,其CH节点没有分布控制和连接性保证,所以丢包率较高,大大减少了数据转发能耗,所以网络生存时间较长.
|
图 3 网络生存时间 |
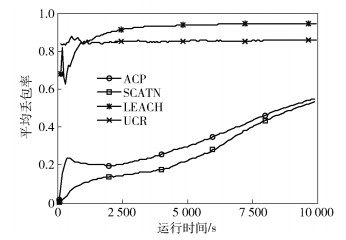
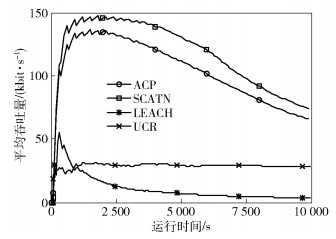
在单位数据能耗从5×10-9 J/bit~200×10-9 J/bit的多组实验中,LEACH、UCR、ACP和SCATN的平均丢包率对比如图 4所示,平均吞吐量对比如图 5所示.从图 4和图 5中可以看出,与LEACH、UCR、ACP相比,SCATN能够有效降低丢包率,提高吞吐量.这是因为SCATN对整个网络进行负载均衡控制,能够有效减缓能量空洞,并且SCATN对转发节点进行连接性和存在性检查,能够保证转发节点有更好的分布和连接性;而LEACH、UCR没有进行分布控制,CH分布不均匀,且没有进行连接性检查,导致丢包率较高和吞吐量较低;ACP在选择CH时通过调整簇范围保证连接性,但是在进行角色转换的时候没有分布控制和连接性检查.随着网络运行时间的增长,不同协议的丢包率和吞吐量之间的差距逐渐减小,这是因为能量空洞问题固有,长时间运行后靠近sink的节点逐渐死亡.
|
图 4 sink丢包率 |
|
图 5 sink吞吐量 |
作为大数据时代重要数据来源的WSN,其感知数据越来越复杂,数据规模越来越大,超出了网络的传输能力,需要在网络中进行数据计算.为此,笔者提出了SCATN聚簇算法,使用计算节点进行数据计算,使用转发节点进行数据转发,并控制它们的分布,从而实现整个网络的负载均衡,缓解热点问题和能量空洞问题.仿真实验验证了在不同的数据计算能耗下该方法的有效性.在以后的工作中,将关注节点休眠机制与聚簇算法的结合,由CCH进行节点的休眠调度,并进一步在聚簇结构的基础上进行服务发现、服务选择、服务中断恢复等服务计算的研究,以验证算法的有效性.
| [1] | Li Chao, Hu Yang, Liu Longjun, et al. Towards sustainable in-situ server systems in the big data era[C]//2015 International Symposium on Computer Architecture. New York: ACM, 2015: 14-26. |
| [2] |
张人上, 曲开社. 基于双簇首网格调度的WSNs能量空洞缓解[J]. 传感器与微系统, 2014, 33(10): 133–136.
Zhang Renshang, Qu Kaishe. Energy hole alleviation of WSNs based on dual cluster head grid scheduling[J]. Transducer and Microsystem Technologies, 2014, 33(10): 133–136. |
| [3] |
刘壮, 冯欣, 王雁龙, 等. 基于双簇头聚类分簇和数据融合的无线传感器网络路由算法[J]. 吉林大学学报, 2015, 53(5): 1013–1017.
Liu Zhuang, Feng Xin, Wang Yanlong, et al. An improved clustering routing algorithm based on double-CH clustering and data fusion in WSN[J]. Journal of Jilin University, 2015, 53(5): 1013–1017. |
| [4] |
戴志强, 严承, 武正江. 一种新的无线传感器网络非均匀分簇双簇头算法-PUDCH算法[J]. 传感技术学报, 2016, 29(12): 1912–1918.
Dai Zhiqiang, Yan Cheng, Wu Zhengjiang. New uneven double cluster head clustering algorithm for WSN-PUDCH algorithm[J]. Chinese Journal of Sensors and Actuators, 2016, 29(12): 1912–1918. doi: 10.3969/j.issn.1004-1699.2016.12.022 |
| [5] | Mo Yijun, Wang Bang, Liu Wenyu, et al. A sink-oriented layered clustering protocol for wireless sensor networks[J]. Mobile Networks and Applications, 2013, 18(5): 639–650. doi: 10.1007/s11036-013-0443-1 |
| [6] | Afsar M M, Younis M. An energy-and proximity-based unequal clustering algorithm for wireless sensor networks[C]//LCN 2014. Washington DC: IEEE Computer Society, 2014: 262-269. |
| [7] | Vural S, Navaratnam P, Wang Ning, et al. Asynchronous clustering of multihop wireless sensor networks[C]//ICC 2014. Piscatawaty: IEEE Press, 2014: 472-477. |
| [8] |
吴标, 崔琛, 余剑, 等. 基于非均匀成簇的无线传感器网络多跳路由算法[J]. 计算机科学, 2017, 44(2): 157–162.
Wu Biao, Cui Chen, Yu Jian, et al. Multi-hop routing algorithm for wireless sensor networks based on uneven clustering[J]. Computer Science, 2017, 44(2): 157–162. |
| [9] |
刘唐, 彭舰, 陈果, 等. 基于密度控制的传感器网络能量空洞避免策略[J]. 计算机学报, 2016, 39(5): 993–1006.
Liu Tang, Peng Jian, Chen Guo, et al. Avoidance of energy hole problem based on density control mechanism for wireless sensor networks[J]. Chinese Journal of Computers, 2016, 39(5): 993–1006. |


