2. 北京航空航天大学 机械工程及自动化学院, 北京 100191
为了提高水龙头等工件的抛光效率,提高抛光精度及质量,设计了新型多工位工作岛式抛光机器人.为使该机器人结构更加紧凑,在建立抛光机器人运动学和逆运动学方程基础上,分析了该机器人的灵活加工空间,提出采用多目标的粒子群法对抛光机器人的多个布局参数进行优化分析.该方法同时对抛光机器人的2个重要布局参数进行了优化,并应用粒子群法计算该机器人抛光不同大小工件时各自由度的最大关节空间.最后通过分析抛光机器人在不同工作平面上的灵活加工点验证了优化结果的正确性.实验结果表明,优化布局后的机器人完全能满足指定工件的抛光加工需求,并有较大的加工余量,获得了较好的实验抛光效果.
2. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China
In order to improve the efficiency of the workpiece such as faucet polishing and improve the polishing precision, quality, a new multi station working island type polishing robot was designed. In order to make this robot structure more compact, based on the establishment of the polishing robot's kinematics and inverse kinematics equations, further analysis of robot flexible working space was carried out, multi-objective particle swarm optimization method was also proposed to analyze and optimize the multiple layout parameters of this robot., then the various degree of freedom joint space was obtained by particle swarm optimization method while robot polishing deferent size workpiece. Finally, the dexterous machining points of the polishing robot is analyzed, which is verified that the optimized layout parameters is suitable. Through the above analysis. It is shown that the robot with optimized layout parameters can fully meet the specified workpiece polishing requirements, and there is a large machining allowance, better experimental polishing effect was obtained finally.
抛光加工是许多产品终加工的重要方式之一,随着人们对产品的质量要求不断提高,以往应用人工或传统机床进行抛光加工的方式越来越难以满足生产的需要,而且抛光加工存在工作环境恶劣、容易产生粉尘爆炸等危险,设计能满足现代生产需要的抛光系统成为亟待解决的问题.相对于传统的机床加工,机器人具有灵活性高、工作空间大等显著优势.机器人在磨削抛光、铣削等加工领域也逐渐得到了应用,国内外有不少学者针对机器人加工开展了大量的研究[1-4].目前不少学者研究了并联机器人应用于加工并进行了优化分析[5-6].机器人加工系统一般都是由工件坐标系和工具坐标系两部分组成的,这两部分如何布局对于增加机器人加工的适应范围、提高机器人加工的效果具有重大的意义.因此对于机器人的布局也有不少学者进行了大量研究[7-14],针对机器人优化大多采用遗传算法、粒子群算法、神经网络等智能算法.本研究设计了新型的工作岛式的多工位抛光机器人,该机器人自由度分布在两边,类似双臂机器人.这种双臂机器人需要对两机器臂的布局参数进行优化,使得机器人在满足工作要求的前提下尺寸尽量小,结构尽量紧凑,工作空间尽量大,工作更灵活.针对双臂机器人的优化及机器人布局也有不少研究成果[15-18],但这些研究成果主要针对传统串联机器人与工件的布局或双串联机器人协同工作时的布局开展,而针对抛光需求设计的机器人的研究成果较少.基于此,笔者将根据抛光需求设计的PPPR+RR构型的抛光机器人的结构布局进行优化研究.
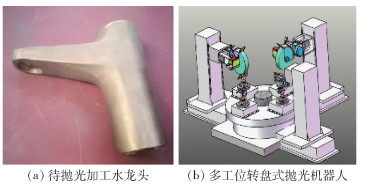
1 抛光机器人本体 1.1 抛光机器人结构水龙头(见图 1(a))等卫浴产品具有批量大、外观要求高等生产特点.为了提高水龙头抛光生产的效率,减少装卡次数,设计了图 1(b)所示的工作岛式水龙头抛光系统.
|
图 1 多工位转盘式抛光机器人及工件 |
如图 1(b)所示,整个抛光机器人中间转盘部分有4个水龙头装卡工位(4个装卡工位中的3个工位进行生产,剩下的1个工位为上下料工位),在转盘的外面布置了3个抛光机器人(3个抛光机器人可以同时进行抛光生产).
1.2 抛光流程上述结构的水龙头抛光机器人按照下面的步骤进行抛光生产:①在上料工位安装上水龙头;②该水龙头安装工位对应的粗抛机器人对该水龙头进行抛光;③粗抛结束,转盘转动90°,粗抛完成的水龙头工位对准中抛机器人进行中级抛光加工;④中抛结束,转盘再转动90°,中抛完成的水龙头工位对准精抛机器人进行精抛加工;⑤精抛完成,转盘转动90°,取下完成精加工的水龙头,装上需要加工的水龙头继续进行粗抛加工.从上述水龙头抛光工艺流程及加工过程来看,这种结构的抛光机器人具有以下4个突出的优点:①多工位同时加工,加工效率高;②工件只需一次装卡;③所有待抛光的水龙头可以经过本机器人完成从粗到精的完整抛光,做到从毛坯到成品的加工过程;④各工位的加工程序只需调整少数参数基本可以通用.
1.3 抛光机器人自由度分析该抛光机器人各自由度分布如图 2所示.

|
图 2 抛光机器人自由度分布图 |
由图 2可以看出,该机器人的自由度被分配到2个部分,中间转盘有B、C 2个转动自由度,四周的抛光机器人有X、Y、Z、A 4个自由度.自由度分配有利于提高抛光机器人的工作空间.
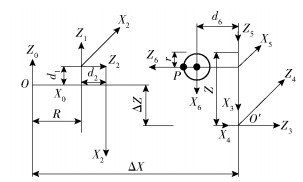
2 抛光机器人运动学分析 2.1 运动学正解由图 2可以看出,该抛光机器人的自由度为RR+PPPR分布,故可以分别建立2个坐标系({O}坐标系和{O′}坐标系),如图 3所示.
|
图 3 坐标系 |
图 3中{O}坐标系为卡具坐标系,原点O为转盘上表面的中心,该坐标系与转盘中央的卡具B、C轴固连,则卡具{O}坐标系D-H参数如表 1所示.其中R为中间转盘的半径.
|
|
表 1 卡具{O}坐标系D-H参数表 |
根据卡具坐标系的D-H参数得到卡具坐标系的转换矩阵:
| $ {\mathit{\boldsymbol{T}}_{02}} = {\mathit{\boldsymbol{T}}_{01}}{\mathit{\boldsymbol{T}}_{12}} = \left[ {\begin{array}{*{20}{c}} { - {{\rm{c}}_1}{{\rm{c}}_2}}&{ - {{\rm{c}}_1}{{\rm{s}}_2}}&{{{\rm{s}}_1}}&{R + {d_2}{{\rm{s}}_1}}\\ { - {{\rm{c}}_2}{{\rm{s}}_1}}&{ - {{\rm{s}}_{\rm{1}}}{{\rm{s}}_2}}&{ - {{\rm{c}}_1}}&{ - {d_2}{{\rm{c}}_1}}\\ {{{\rm{c}}_2}}&{ - {{\rm{s}}_2}}&0&{{d_1}}\\ 0&0&0&1 \end{array}} \right] $ | (1) |
设工件坐标系为{W},其坐标原点为卡具的末端点,则工件坐标系{W}相对{O}坐标系有
| $ {\mathit{\boldsymbol{T}}_{OW}} = {\mathit{\boldsymbol{T}}_{02}}{\mathit{\boldsymbol{T}}_{2W}} $ | (2) |
根据Z-Y-Z欧拉角定理,则工件坐标系{W}相对于式(2)可描述为
| $ \begin{array}{c} {\mathit{\boldsymbol{T}}_{2W}} = \\ \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\alpha {\rm{c}}\beta {\rm{c}}\gamma - {\rm{s}}\alpha {\rm{s}}\gamma }&{ - {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma - {\rm{s}}\alpha {\rm{c}}\gamma }&{{\rm{c}}\alpha {\rm{s}}\beta }&{{p_X}}\\ {{\rm{s}}\alpha {\rm{c}}\beta {\rm{c}}\gamma + {\rm{c}}\alpha {\rm{s}}\gamma }&{{\rm{c}}\alpha {\rm{c}}\gamma - {\rm{s}}\alpha {\rm{c}}\beta {\rm{s}}\gamma }&{{\rm{s}}\alpha {\rm{s}}\beta }&{{p_Y}}\\ { - {\rm{s}}\beta {\rm{c}}\gamma }&{{\rm{s}}\beta {\rm{s}}\gamma }&{{\rm{c}}\beta }&{{p_Z}}\\ 0&0&0&1 \end{array}} \right] \end{array} $ | (3) |
由式(1)~式(3)可得
| $ {\mathit{\boldsymbol{T}}_{oW}} = \left[ {\begin{array}{*{20}{c}} {{n_X}}&{{o_X}}&{{a_X}}&{{P_X}}\\ {{n_Y}}&{{o_Y}}&{{a_Y}}&{{P_Y}}\\ {{n_Z}}&{{o_Z}}&{{a_Z}}&{{P_Z}}\\ 0&0&0&1 \end{array}} \right] $ | (4) |
其中
| $ \begin{array}{l} \left. \begin{array}{l} {n_X} = {{\rm{c}}_1}{{\rm{c}}_2}({\rm{s}}\alpha {\rm{s}}\gamma - {\rm{c}}\alpha {\rm{c}}\beta {\rm{c}}\gamma ) - \\ \;\;\;\;\;\;\;{{\rm{c}}_1}{{\rm{s}}_2}({\rm{c}}\alpha {\rm{s}}\gamma + {\rm{c}}\beta {\rm{c}}\gamma {\rm{s}}\alpha ) - {\rm{c}}\gamma {\rm{s}}\beta {{\rm{s}}_1}\\ {n_Y} = {{\rm{c}}_2}{{\rm{s}}_1}({\rm{s}}\alpha {\rm{s}}\gamma - {\rm{c}}\alpha {\rm{c}}\beta {\rm{c}}\gamma ) - \\ \;\;\;\;\;\;\;{{\rm{s}}_1}{{\rm{s}}_2}({\rm{c}}\alpha {\rm{s}}\gamma + {\rm{c}}\beta {\rm{c}}\gamma {\rm{s}}\alpha ) + {\rm{c}}\gamma {\rm{s}}\beta {{\rm{c}}_1}\\ {n_Z} = {{\rm{s}}_2}({\rm{c}}\alpha {\rm{s}}\gamma + {\rm{c}}\beta {\rm{c}}\gamma {\rm{s}}\alpha ) - \\ \;\;\;\;\;\;\;{{\rm{c}}_2}({\rm{s}}\alpha {\rm{s}}\gamma - {\rm{c}}\alpha {\rm{c}}\beta {\rm{c}}\gamma ) \end{array} \right\}\\ \left. \begin{array}{l} {o_X} = {{\rm{c}}_1}{{\rm{c}}_2}({\rm{s}}\alpha {\rm{c}}\gamma + {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma ) - \\ \;\;\;\;\;\;\;{{\rm{c}}_1}{{\rm{s}}_2}({\rm{c}}\alpha {\rm{c}}\gamma - {\rm{c}}\beta {\rm{s}}\gamma {\rm{s}}\alpha ) + {\rm{s}}\gamma {\rm{s}}\beta {{\rm{s}}_1}\\ {o_Y} = {{\rm{c}}_2}{{\rm{s}}_1}({\rm{c}}\gamma {\rm{s}}\alpha + {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma ) - \\ \;\;\;\;\;\;{{\rm{s}}_1}{{\rm{s}}_2}({\rm{c}}\alpha {\rm{c}}\gamma - {\rm{c}}\beta {\rm{s}}\alpha {\rm{s}}\gamma ) - {\rm{s}}\beta {{\rm{c}}_1}{\rm{s}}\gamma \\ {o_Z} = {{\rm{s}}_2}({\rm{c}}\alpha {\rm{c}}\gamma - {\rm{c}}\beta {\rm{s}}\alpha {\rm{s}}\gamma ) - \\ \;\;\;\;\;\;\;{{\rm{c}}_2}({\rm{c}}\gamma {\rm{s}}\alpha + {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma ) \end{array} \right\}\\ \left. \begin{array}{l} {a_X} = {\rm{c}}\beta {{\rm{s}}_1} - {\rm{c}}\alpha {\rm{s}}\beta {{\rm{c}}_1}{{\rm{c}}_2} - {\rm{s}}\alpha {\rm{s}}\beta {{\rm{c}}_1}{{\rm{s}}_2}\\ {a_Y} = - {\rm{c}}\beta {{\rm{c}}_1} - {\rm{c}}\alpha {\rm{s}}\beta {{\rm{s}}_2}{{\rm{s}}_1} - {\rm{s}}\alpha {\rm{s}}\beta {{\rm{s}}_1}{{\rm{s}}_2}\\ {a_Z} = {\rm{c}}\alpha {\rm{s}}\beta {{\rm{c}}_2} + {\rm{s}}\alpha {\rm{s}}\beta {{\rm{s}}_2} \end{array} \right\}\\ \left. \begin{array}{l} {P_X} = R + {{\rm{s}}_1}{d_2} + {p_Z}{{\rm{s}}_1} - {p_X}{{\rm{c}}_1}{{\rm{c}}_2} - {p_Y}{{\rm{c}}_1}{{\rm{s}}_2}\\ {P_Y} = - {{\rm{c}}_1}{d_2} - {p_Z}{{\rm{c}}_1} - {p_X}{{\rm{c}}_2}{{\rm{s}}_1} - {p_Y}{{\rm{s}}_1}{{\rm{s}}_2}\\ {P_Z} = {d_1} + {p_X}{{\rm{c}}_2} + {p_Y}{{\rm{s}}_2} \end{array} \right\} \end{array} $ | (5) |
其中:γ为抛光轮半径,si、ci分别为sinθi、cosθi的缩写,sα、sβ、sγ分别表示sinα、sinβ和sinγ,cα、cβ、cγ分别表示cosα、cosβ和cosγ. 图 3中工具坐标系{O′}为外围XYZA抛光机器人坐标系,该坐标系的原点为X、Y、Z轴的交点,该坐标系与抛光轮固连,如果把抛光轮的旋转及抛光轮轮径的变化当作2个自由度来看待,则其D-H参数如表 2所示.
|
|
表 2 工具坐标系{O′}D-H参数表 |
根据工具坐标系的D-H参数得到工具坐标系的转换矩阵:
| $ \begin{array}{c} {\mathit{\boldsymbol{T}}_{O' 8}} = {\mathit{\boldsymbol{T}}_{O' 3}}{\mathit{\boldsymbol{T}}_{34}}{\mathit{\boldsymbol{T}}_{45}}{\mathit{\boldsymbol{T}}_{56}}{\mathit{\boldsymbol{T}}_{67}}{\mathit{\boldsymbol{T}}_{78}} = \\ \left[ {\begin{array}{*{20}{c}} {{{\rm{c}}_3}{{\rm{c}}_4}}&{{{\rm{s}}_3}}&{{{\rm{c}}_3}{{\rm{s}}_4}}&{Z + r{{\rm{c}}_3}{{\rm{s}}_4}}\\ { - {{\rm{c}}_4}{{\rm{s}}_3}}&{{{\rm{c}}_3}}&{ - {{\rm{s}}_3}{{\rm{s}}_4}}&{ - Y - r{{\rm{s}}_3}{{\rm{s}}_4}}\\ { - {{\rm{s}}_4}}&0&{{{\rm{c}}_4}}&{X - {d_6} + r{{\rm{c}}_4}}\\ 0&0&0&1 \end{array}} \right] \end{array} $ | (6) |
{O′}坐标系的X、Z轴方向分别与{O}坐标系Z、X轴的方向相同,{O}坐标系在中间,{O′}坐标系在外面,2个坐标系之间有一定的位置偏移,即外面XYZA机器人相对中间卡具B、C轴的布局参数,这个布局参数就是{O′}坐标系相对{O}坐标系X轴和Z轴分别有ΔX和ΔZ的偏移,则工具坐标系{O′}相对于卡具坐标系{O}的转换矩阵为
| $ \begin{array}{c} {\mathit{\boldsymbol{T}}_{O8}} = \\ \left[ {\begin{array}{*{20}{c}} { - {{\rm{s}}_4}}&0&{{{\rm{c}}_4}}&{X - {d_6} + r{{\rm{c}}_4} + \Delta X}\\ { - {{\rm{c}}_4}{{\rm{s}}_3}}&{{{\rm{c}}_3}}&{ - {{\rm{s}}_3}{{\rm{s}}_4}}&{ - Y - r{{\rm{s}}_3}{{\rm{s}}_4}}\\ {{{\rm{c}}_3}{{\rm{s}}_4}}&{{{\rm{s}}_3}}&{{{\rm{c}}_3}{{\rm{c}}_4}}&{Z + r{{\rm{c}}_3}{{\rm{s}}_4} + \Delta Z}\\ 0&0&0&1 \end{array}} \right] \end{array} $ | (7) |
工件表面抛光点与工具坐标系工作点重合,有
| $ {\mathit{\boldsymbol{T}}_{O8}} = {\mathit{\boldsymbol{T}}_{OW}} $ | (8) |
存在以下方程组:
| $ \left. \begin{array}{l} {{\rm{c}}_1}{{\rm{c}}_2}({\rm{s}}\alpha {\rm{c}}\gamma + {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma ) - {{\rm{c}}_1}{{\rm{s}}_2}({\rm{c}}\alpha {\rm{c}}\gamma - \\ \;\;\;\;\;\;{\rm{c}}\beta {\rm{s}}\gamma {\rm{s}}\alpha ) + {\rm{s}}\gamma {\rm{s}}\beta {{\rm{s}}_1} = 0\\ {{\rm{c}}_1}{{\rm{c}}_2}({\rm{s}}\alpha {\rm{s}}\gamma - {\rm{c}}\alpha {\rm{c}}\beta {\rm{c}}\gamma ) - {\rm{c}}\gamma {\rm{s}}\beta {{\rm{s}}_1} - \\ \;\;\;\;\;\;{{\rm{c}}_1}{{\rm{s}}_2}({\rm{c}}\alpha {\rm{s}}\gamma + {\rm{c}}\beta {\rm{c}}\gamma {\rm{s}}\alpha ) = - {{\rm{s}}_4}\\ {a_X} = {\rm{c}}\beta {{\rm{s}}_1} - {\rm{c}}\alpha {\rm{s}}\beta {{\rm{c}}_1}{{\rm{c}}_2} - {\rm{s}}\alpha {\rm{s}}\beta {{\rm{c}}_1}{{\rm{s}}_2} = {{\rm{c}}_4}\\ {{\rm{s}}_2}({\rm{c}}\alpha {\rm{c}}\gamma - {\rm{c}}\beta {\rm{s}}\alpha {\rm{s}}\gamma ) - {{\rm{c}}_2}({\rm{c}}\gamma {\rm{s}}\alpha + {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma ) = {{\rm{s}}_3}\\ R + {{\rm{s}}_1}{d_2} + {p_Z}{{\rm{s}}_1} - {p_X}{{\rm{c}}_1}{{\rm{c}}_2} - {p_Y}{{\rm{c}}_1}{{\rm{s}}_2} = \\ \;\;\;\;\;\;\;X - {d_6} + r{{\rm{c}}_4} + \Delta X - \\ \;\;\;\;\;\;{{\rm{c}}_1}{d_2} - {p_Z}{{\rm{c}}_1} - {p_X}{{\rm{c}}_2}{{\rm{s}}_1} - {p_Y}{{\rm{s}}_1}{{\rm{s}}_2} = - Y - r{{\rm{s}}_3}{{\rm{s}}_4}\\ {d_1} + {p_X}{{\rm{c}}_2} + {p_Y}{{\rm{s}}_2} = Z + r{{\rm{c}}_3}{{\rm{s}}_4} + \Delta Z \end{array} \right\} $ | (9) |
为书写方便,则定义
| $ \left. \begin{array}{l} {C_1} = {{\rm{c}}_1}{{\rm{c}}_2}\\ {A_1} = ({\rm{s}}\alpha {\rm{c}}\gamma + {\rm{c}}\alpha {\rm{s}}\beta{\rm{s}}\gamma )\\ {C_2} = {{\rm{c}}_1}{{\rm{s}}_2}\\ {B_1} = ({\rm{c}}\alpha {\rm{c}}\gamma - {\rm{c}}\beta {\rm{s}}\gamma {\rm{s}}\alpha )\\ {C_3} = {\rm{s}}\gamma {\rm{s}}\beta\\ D = ({\rm{s}}\alpha {\rm{s}}\gamma - {\rm{c}}\alpha {\rm{c}}\beta {\rm{c}}\gamma )\\ E = ({\rm{c}}\alpha {\rm{s}}\gamma + {\rm{c}}\beta {\rm{c}}\gamma {\rm{s}}\alpha )\\ F = {\rm{c}}\gamma {\rm{s}}\beta\\ G = {\rm{c}}\beta \\ H = {\rm{c}}\alpha {\rm{s}}b\\ I = {\rm{s}}\alpha {\rm{s}}\beta\\ J = ({\rm{c}}\alpha {\rm{c}}\gamma - {\rm{c}}\beta {\rm{s}}\alpha {\rm{s}}\gamma )\\ K = ({\rm{c}}\gamma {\rm{s}}\alpha + {\rm{c}}\alpha {\rm{s}}\beta{\rm{s}}\gamma ) \end{array} \right\} $ | (10) |
解得
| $ \left. \begin{array}{l} {C_2} = \frac{{{C_3}({A_1}F + {C_3}D){\rm{ }}{c_4}}}{{({C_3}I - {B_1}G)(({A_1}F + {C_3}D)}} \cdots \\ \;\;\;\;\;\;\;\;\frac{{ - {C_3}({A_1}G + H{C_3}){\rm{ }}{s_4}}}{{ - ({B_1}F + {C_3}E)({A_1}G + H{C_3})}}\\ {C_1} = \frac{{({B_1}F + {C_3}E){\rm{ }}{C_2} - {C_3}{s_4}}}{{({A_1}F + {C_3}D)}} \end{array} \right\} $ | (11) |
| $ \left. \begin{array}{l} {s_1} = \frac{{{B_1}{C_2} - {A_1}{C_1}}}{{{C_3}}}\\ {t_2} = \frac{{{C_2}}}{{{C_1}}}\\ {s_3} = J{s_2} - K{c_2}\\ X = R + {p_Z}{s_1} - {p_X}{c_1}{c_2} - \\ \;\;\;\;\;\;\;\;{p_Y}{c_1}{s_2} - r{c_4} - \Delta X + {d_6} + {d_2}{s_1}\\ Y = {d_2}{c_1} + {p_Z}{c_1} + {p_X}{c_2}{s_1} + {p_Y}{s_1}{s_2} - r{s_3}{s_4}\\ Z = {d_1} + {p_X}{c_2} + {p_Y}{s_2} - r{c_3}{s_4} - \Delta Z \end{array} \right\} $ | (12) |
若机器人结构参数d1、d2、d6、R、r、θ4及布局参数ΔX、ΔZ和工件参数α、β、γ、PX、PY、pZ已知,根据式(11)则可得机器人变量X、Y、Z、θ1、θ2、θ3:
| $ \left. \begin{array}{l} {\theta _1} = {f_1}({d_1}, {d_2}, {d_6}, R, r, {\theta _4}, \Delta X, \Delta Z, {p_X}, {p_Y}, {p_Z}, \alpha , \beta , \gamma )\\ {\theta _2} = {f_2}({d_1}, {d_2}, {d_6}, R, r, {\theta _4}, \Delta X, \Delta Z, {p_X}, {p_Y}, {p_Z}, \alpha , \beta , \gamma )\\ {\theta _3} = {f_3}({d_1}, {d_2}, {d_6}, R, r, {\theta _4}, \Delta X, \Delta Z, {p_X}, {p_Y}, {p_Z}, \alpha , \beta , \gamma )\\ X = {f_4}({d_1}, {d_2}, {d_6}, R, r, {\theta _4}, \Delta X, \Delta Z, {p_X}, {p_Y}, {p_Z}, \alpha , \beta , \gamma )\\ Y = {f_5}({d_1}, {d_2}, {d_6}, R, r, {\theta _4}, \Delta X, \Delta Z, {p_X}, {p_Y}, {p_Z}, \alpha , \beta , \gamma )\\ Z = {f_6}({d_1}, {d_2}, {d_6}, R, r, {\theta _4}, \Delta X, \Delta Z, {p_X}, {p_Y}, {p_Z}, \alpha , \beta , \gamma ) \end{array} \right\} $ | (13) |
设待抛光工件的尺寸范围在(200 mm×200 mm×200 mm),为了分析本抛光机器人的抛光灵活度,只需pX、pY、pZ在200 mm范围内遍历取值,α、β、γ在(0~2π)范围内遍历取值,如果当前取值根据式(13)求解的各自由度变量在行程范围内,则该点为灵活加工点,否则就不是该状态下的灵活加工点.定义抛光机器人灵活度为
| $ f = \frac{n}{m} $ | (14) |
其中:n为遍历的所有灵活姿态加工点的总数,m为所有遍历点的总数. f=0表示该点为不可加工点;f=1表示任意姿态角的工件上的该加工点抛光机器人均可以加工;0 < f < 1表示该点为灵活加工点. f越大意味着对于工件上的待加工点抛光机器人可以以更多灵活的姿态完成加工.经过分析,工件尺寸在(200 mm×200 mm×200 mm)以内的均可以加工.按照式(14)灵活度的定义,该机器人的灵活度为0.44.影响灵活度的主要因素是求解θ1不成功,分析反解式(11)可以看出,当sinβ×sinγ值很小时对θ1的求解容易失败, 即在工件姿态角度sinβ×sinγ值很小时,抛光机器人对该工件加工时如果要按照某种特定参数加工,则按式(14)定义的灵活度小些.经过分析,工件尺寸在(200 mm×200 mm×200 mm)范围内甚至3倍这个范围,本机器人均可以完成对工件的抛光加工.
3.2 抛光机器人布局优化通过前面的分析可知,抛光机器人的可达工作空间及灵活工作空间均很大.但本抛光机器人的待加工工件并不是很大,对抛光机器人工作空间要求没有太大,故可对本机器人的结构进行优化.
由于转盘上有4个工件夹具,转盘中间需要放置部分电气元件,故转盘半径R应根据实际情况确定.针对同样大小的被加工件来说,依据式(13),影响抛光机器人灵活加工空间的主要是ΔX和ΔZ这2个参数.同时,这2个参数就是抛光机器人工件坐标系与工具坐标系的相对位置,也就是外面4自由度机器人相对于中间转盘的放置位置.
因此,针对抛光机器人外面4自由度机器人与中间2自由度夹具的位置布局参数进行优化,可以在保证抛光机器人灵活工作空间的前提下让机器人的结构更加紧凑.
1) 优化目标
使结构更加紧凑,故ΔX最小,在建立坐标系方程时,ΔZ为负数,故要ΔZ最大尽量趋近于0,具体的目标函数为
| $ \left. \begin{array}{l} \Delta X = R + {d_2}{{\rm{s}}_1} + {p_Z}{{\rm{s}}_1} - \\ \;\;\;\;\;\;\;\;{p_Y}{{\rm{c}}_1}{{\rm{s}}_2} - r{{\rm{c}}_4} + {d_6} - X - {p_X}{{\rm{c}}_1}{{\rm{c}}_2}\\ \Delta Z = {d_1} + {p_X}{{\rm{c}}_2} + {p_Y}{{\rm{s}}_2} - r{{\rm{c}}_3}{{\rm{s}}_4} - Z \end{array} \right\} $ | (16) |
2) 约束条件
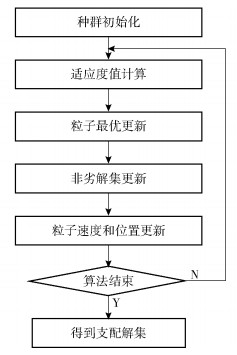
对于上述2个参数的优化要满足的约束条件是抛光机器人的灵活抛光空间能满足加工工件尺寸要求,同时抛光机器人各自由度取值在行程范围内.参数优化方法有很多,比较典型的有遗传算法、粒子群法、免疫优化算法、模拟退火法、蚁群算法等.许多优化问题各种方法也都能实现,但各种方法也都有些缺陷.本优化问题的待优化目标是多个,多目标的优化可以采用多目标遗传算法等,但遗传算法存在易陷入局部最优的问题,因此采用多目标的粒子群法进行优化.基于粒子群的多目标优化应用比较广泛,在机器人路径规划[19-20]及其他行业的优化[21]里面都得到了广泛应用.基于粒子群的多目标值优化流程如图 4所示.
|
图 4 粒子群法多目标值优化流程 |
该优化项目的目标函数及约束为
| $ \left. \begin{array}{l} {F_{{\rm{1min}}}} = R + {d_2}{{\rm{s}}_1} + {p_Z}{{\rm{s}}_1} - {p_X}{{\rm{c}}_1}{{\rm{c}}_2} - \\ \;\;\;\;\;\;\;{p_Y}{{\rm{c}}_1}{{\rm{s}}_2} - r{{\rm{c}}_4} + {d_6} - X\\ {F_{{\rm{2max}}}} = {d_1} + {p_X}{{\rm{c}}_2} + {p_Y}{{\rm{s}}_2} - r{{\rm{c}}_3}{{\rm{s}}_4} - Z\\ Y = {d_2}{{\rm{c}}_1} + {p_Z}{{\rm{c}}_1} - r{{\rm{s}}_3}{{\rm{s}}_4} + {p_X}{{\rm{c}}_2}{{\rm{s}}_1} + {p_Y}{{\rm{s}}_1}{{\rm{s}}_2}\\ - 400 \le Y \le 500 \end{array} \right\} $ | (16) |
结合式(11)和式(16),将相关的参数(见表 3)粒子化进行迭代优化.
|
|
表 3 粒子化参数表 |
粒子迭代更新公式为
| $ \left. \begin{array}{l} {V^{k + 1}} = \omega {V^k} + {c_1}{r_1}(P_{id}^{^k} - {X^k}) + {c_2}{r_2}(P_{gd}^{^k} - {X^k})\\ {X^{k + 1}} = {X^k} + {V^{k + 1}} \end{array} \right\} $ | (17) |
其中:ω为惯性权重,r1、r2为分布于[0, 1]之间的随机数,K为当前迭代次数,Pidk为个体最优粒子位置,Pgdk为全局最优粒子位置,c1、c2为常数,V为粒子速度,X为粒子位置.
粒子群算法采用的参数如表 4所示.
|
|
表 4 多目标粒子群算法参数设置表 |
惯性权重为
| $ \omega = {\omega _{{\rm{max}}}} - \frac{{I({\omega _{{\rm{max}}}} - {\omega _{{\rm{min}}}})}}{M} $ | (18) |
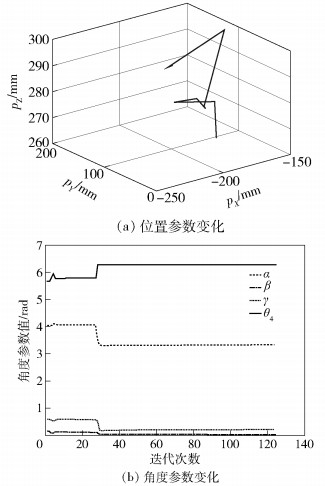
其中:M为总迭代次数,I为当前迭代次数.按照上述参数应用多目标优化的粒子群法获取该抛光机器人的布局参数过程如图 5及图 6所示.
|
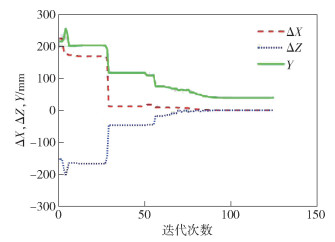
图 5 布局参数迭代过程中粒子变化过程 |
|
图 6 布局参数优过程 |
在粒子种群设为300时,经过124次左右的迭代,最后收敛值如表 5所示.
|
|
表 5 粒子群法迭代结果表 |
在实际分析优化中,对抛光机器人的所有参数都粒子化在各自的取值范围内进行迭代进化.考虑到加工的余量,实际优化时对工件尺寸放大到(300 mm×300 mm×300 mm)进行计算.按照多目标法优化出ΔX和ΔZ的优化结果如图 6及表 5所示,可以看出ΔX和ΔZ的最优结果都接近于0,如果都等于0,则显示结构最紧凑.
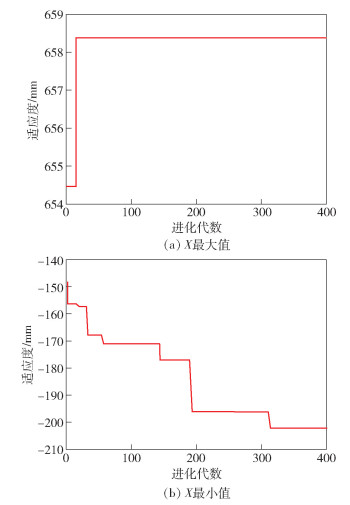
实际生产中结合安装、操作方便等因素,最后ΔZ考虑到转盘高度设计尺寸500 mm,ΔX考虑到抛光头的尺寸及其他设备的安装设计尺寸650 mm.按照这2个参数代入式(11)计算抛光机器人对不同尺寸范围的水龙头进行抛光时各移动关节空间范围.采用粒子群法求抛光机器人加工指定工件时所需X轴关节空间范围的过程如图 7所示.
|
图 7 粒子群法求解抛光加工所需X轴关节空间优化过程 |
针对不同尺寸工件进行抛光时,抛光机器人X、Y、Z行程最大范围如表 6所示.
|
|
表 6 不同大小工件所需最大机器人行程表 |
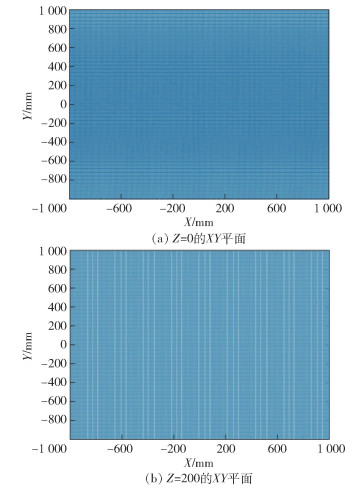
用这些优化后的参数变量求抛光机器人的灵活工作空间点,分别取Z=0和Z=200的XY平面进行验证,如图 8所示.
|
图 8 灵活抛光点分布图 |
由图 8可知,在XY平面的2 000 mm×2 000 mm范围内均是抛光点,加工范围远远大于所提出的工件尺寸范围,能够满足抛光加工的需求.
4 实验 4.1 整体实验及布局处理转盘式多工位抛光机器人整体布局如图 9所示.从图中可以看出,为了让该机器人结构紧凑,满足抛光加工需求,中间转盘下面焊接了一个底座,并在中间转盘和外围机器人间焊接了一段,目的就是为了满足{O}和{O′}坐标系的偏差最小.

|
图 9 转盘式多工位抛光机器人布局图 |
优化布局的结果显示,ΔZ和ΔX都取0时,结构最紧凑.如图 9所示,对ΔZ的处理是为了使抛光机器人的抛光头部分在Z轴方向Z自由度的取值为0时,抛光轮的中心与BC轴线交点位于同一水平面上.对ΔX的处理是为了使X轴方向X自由度取值为0时,抛光轮的中心与B轴线在同一竖直平面上.这样,理论建模的ΔZ和ΔX取值就为0.
4.2 加工实验结论按照上述分析,对抛光机器人内外2个坐标系的布局参数ΔX和ΔZ进行处理,能够达到既满足加工要求,又保证结构紧凑的目的.
利用转盘式多工位抛光机器人进行水龙头抛光加工前后如图 10所示.

|
图 10 抛光工件 |
针对所设计的一种新式的多工位工作岛式抛光机器人进行运动学分析,应用粒子群法对该机器人的布局进行分析和优化,综合考虑实际操作情况及现场状况得到最合适的布局参数.根据优化后的并考虑实际情况选取的合理参数应用粒子群法分析了机器人加工不同大小工件时各自由度所需的最大行程,根据前述分析得到了抛光机器人的灵活加工点,验证了当前优化参数能满足加工需求.本研究对于分析类似双臂机器人的多参数优化提供了一种思路,下一步需要继续对机器人关节空间进行优化研究,进而得到更科学合理的机器人结构.
| [1] | Mejri S, Gagnol V, Le T P, et al. Dynamic characterization of machining robot and stability analysis[J]. International Journal of Advanced Manufacturing Technology, 2016, 82(1-4): 351–359. doi: 10.1007/s00170-015-7336-3 |
| [2] |
张栋, 贠超, 宋德政, 等. 基于正交试验法的3P3R磨削机器人灵活性优化[J]. 北京航空航天大学学报, 2010, 9(36): 1075–1079.
Zhang Dong, Yun Chao, Song Dezheng, et al. Dexterity optimization based on orthogonal test of 3P3R grinding robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 9(36): 1075–1079. |
| [3] | 张栋. 抛光机器人系统的灵活性与力控制研究[D]. 北京: 北京航空航天大学, 2012. |
| [4] | Guo Yingjie, Dong Huiyue, Ke Yinglin. Stiffness-oriented posture optimization in robotic machining applications[J]. Robotics and Computer-Integrated Manufacturing, 2015, 35(C): 69–76. |
| [5] | Hosseini M A, Daniali H M. Cartesian workspace optimization of tricept parallel manipulator with machining application[J]. Robotica, 2015, 33(9): 1948–1957. doi: 10.1017/S0263574714000861 |
| [6] | Yan Jin, Bi Z M, Liu Haitao, et al. Kinematic analysis and dimensional synthesis of exechon parallel kinematic machine for large volume machining[J]. Journal of Mechanisms and Robotics, 2015, 7(4): 1–15. |
| [7] |
王召莉, 陈卫东. 基于关节空间评估的机器人作业单元布局优化[J]. 上海交通大学学报, 2009, 11(43): 1762–1766.
Wang Zhaoli, Chen Weidong. Robot work cell layout optimization based on joint space valuation[J]. Journal of Shanghai Jiaotong University, 2009, 11(43): 1762–1766. |
| [8] |
项彬彬, 陈卫东, 亓利伟, 等. 基于遗传算法的机器人作业单元布局优化[J]. 上海交通大学学报, 2008, 42(10): 1697–1701.
Xiang Binbin, Chen Weidong, Qi Liwei, et al. Robot work cell layout optimization based on genetic algorithm[J]. Journal of Shanghai Jiaotong University, 2008, 42(10): 1697–1701. doi: 10.3321/j.issn:1006-2467.2008.10.021 |
| [9] | 王召莉. 基于关节空间评估的机器人工作单元布局优化[D]. 上海: 上海交通大学, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D068313 |
| [10] |
王军, 曹春平, 丁武学, 等. 基于遗传算法的双机器人加工中心布局优化[J]. 中国机械工程, 2016, 27(2): 173–178.
Wang Jun, Cao Chunping, Ding Wuxue, et al. Layout optimization on dual-robot machining center based on genetic algorithm[J]. China Mechanical Engineering, 2016, 27(2): 173–178. doi: 10.3969/j.issn.1004-132X.2016.02.006 |
| [11] | Wang Xuewu, Shi Yingpan, Ding Dongyan, et al. Double global optimum genetic algorithm-particle swarm optimization-based welding robot path planning[J]. Engineering Optimization, 2015, 2(48): 299–316. |
| [12] | Vosniakos G, Matsas E. Improving feasibility of robotic milling through robot placement optimization[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(5): 517–525. doi: 10.1016/j.rcim.2010.04.001 |
| [13] | Antnio M Lopes, Pires E J S. Optimization of the workpiece location in a machining robotic cell[J]. International Journal of Advanced Robotic Systems, 2011, 8(6): 37–46. |
| [14] | Gundogdu E, Gultekin H. Scheduling in two-machine robotic cells with a self-buffered robot[J]. ⅡE Transactions, 2015, 2(48): 170–191. |
| [15] | Wang Yunpeng, Cheng Long, Hou Zengguang, et al. Optimal ormation of multirobot systems based on a recurrent neural network[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(2): 322–333. doi: 10.1109/TNNLS.2015.2464314 |
| [16] | Behnoush Rezaeian Jouybari, Kambiz Ghaemi Osgouie, Ali Meghdari. Optimization of kinematic redundancy and workspace analysis of a dual-arm cam-lock robot[J]. Robotica, 2016, 1(34): 23–42. |
| [17] | Alan Oliveira de Sá, Nadia Nedjah, Luiza de Macedo Mourelle. Distributed efficient localization in swarm robotic systems using swarm intelligence algorithm[J]. Neurocomputing, 2016, 8(172): 322–336. |
| [18] | Datta R, Pradhan S, Bhattacharya B. Analysis and design optimization of a robotic gripper using multiobjective genetic algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2016, 46(1): 16–26. doi: 10.1109/TSMC.2015.2437847 |
| [19] |
刘勇, 贾庆轩, 陈钢, 等. 基于多目标粒子群优化算法的自由漂浮空间机器人负载最大化轨迹优化[J]. 机器人, 2014, 36(4): 402–410.
Liu Yong, Jia Qingxuan, Chen Gang, et al. Load maximization trajectory optimization for free-floating space robot using multi-objective particle swarm optimization algorithm[J]. Robot, 2014, 36(4): 402–410. |
| [20] |
王坤坤, 尹怡欣. 基于一种改进PSO的移动机器人路径规划[J]. 北京邮电大学学报, 2006, 29(Sup.2): 70–74.
Wang Kunkun, Yin Yixin. Path planning for mobile robot based on a modified particle warm optimization[J]. Journal of Beijing University of Posts and Telecommunications, 2006, 29(Sup.2): 70–74. |
| [21] |
夏虹, 李增智. 粒子群算法求解Web服务组合中基于QoS的服务选择[J]. 北京邮电大学学报, 2009, 32(4): 63–67.
Xia Hong, Li Zengzhi. A particle swarm optimization algorithm for service selection problem based on quality of service in web services composition[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(4): 63–67. doi: 10.3969/j.issn.1007-5321.2009.04.014 |


