针对具有反馈时延的上行两小区多输入多输出蜂窝干扰网络,提出一种基于发射端混合信道状态信息(CSIT)反馈的回溯干扰中和(RIN)方案.首先,通过用户发送机制设计使基站完成边信息的获取;其次,用户利用CSIT完成预编码并传输至基站;最后,基站利用预编码信息将多个时隙的干扰叠加为零,从而完成小区间干扰的消除.给出了所提RIN方案的适用条件、系统和速率、可达自由度和仿真验证,并将所提方案与时分多址方案和回溯干扰对齐方案进行分析和仿真.仿真结果表明,所提方案能获得更多的系统自由度.
For the uplink two-cell multiple-input multiple-output cellular interfering network with delayed feedback, a retrospective interference neutralization (RIN) scheme was proposed by using hybrid channel state information at the transmitter (CSIT). First, each user was scheduled to send fresh data streams to each base station so that each base station can obtain side information. Subsequently, each user used the hybrid CSIT to precode information and sent the precoding information to each base station. Finally, each base station eliminated all inter-cell interference by using the precoding information. The achievable degrees of freedom, the achievable sum rate, the simulation validation and the application conditions of RIN scheme were given. Experiment shows that the proposed RIN scheme can provide significant degrees of freedom gain over the time division multiple access and the existing retrospective interference alignment schemes.
干扰对齐作为一种有效抑制干扰的干扰管理技术由Cadambe等[1]提出.其基本思想是发射机通过预编码将接收机收到的干扰对齐到更低维度的信号子空间中,从而为期望信号提供更多有效的信号维度.当干扰信道中存在中继时,Gou等[2]发现干扰中和技术能够获得比干扰对齐技术更高的自由度.干扰中和技术作为一种能够消除干扰的干扰管理技术,主要用于解决干扰中继网络和多跳网络中用户间干扰.其基本思想是利用中间节点的天线资源使干扰信号在传播时相互“中和”,从而使接收机只接收到期望信号.自由度(也称为复用增益)作为系统容量的一阶近似,能在高信噪比下定义系统容量.干扰管理技术以最大化系统自由度为目标,已广泛应用于蜂窝干扰网络和多跳网络等.
在蜂窝干扰网络中,由于小区边缘用户受到相邻小区基站的干扰将导致系统容量降低.为了有效压缩小区间干扰的信号维度,谢显中等[3]和Ma等[4]分析了蜂窝干扰网络的自由度,结果表明,虽然干扰对齐技术不能达到自由度上界,但是仍比时分多址(TDMA, time division multiple access)方案获得更多自由度.
上述蜂窝干扰网络的干扰对齐技术研究需要发射端具备完美的信道状态信息(CSIT, channel state information at the transmitter).但在实际的通信环境中,反馈时延等因素的影响不可忽视.当网络中节点获取反馈信息存在时延时,传统干扰对齐技术不能利用当前CSIT进行预编码,从而无法降低干扰信号维度. Shin等[5]提出了利用延时CSIT的回溯干扰对齐(RIA, retrospective interference alignment)方案并将其应用于两小区蜂窝干扰网络,结果表明,该方案能获得比TDMA方案更高的系统自由度.鉴于在实际通信中发射节点有机会在某些时隙获得即传的CSIT,Mohanty等[6]针对具有混合CSIT的多输入多输出(MIMO, multiple-input multiple-output)干扰信道提出了一种基于混合CSIT的干扰管理方案,该方案能获得比基于延时CSIT的RIA方案更高的系统自由度.其中,混合CSIT是指发射端在某些时隙能够获得即传的CSIT,而在剩余的其他时隙则获得具有反馈时延的CSIT.目前,基于混合CSIT反馈的干扰管理方案尚未应用于蜂窝干扰网络.
分析和研究了混合CSIT反馈的上行两小区多用户MIMO蜂窝干扰网络的自由度,提出一种利用混合CSIT反馈的回溯干扰中和(RIN, retrospective interference neutralization)方案.该方案包含边信息提取和回溯干扰传输2个步骤.首先,通过用户发送机制设计使基站完成边信息的提取;其次,用户利用混合CSIT反馈设计波束矩阵完成回溯干扰传输,从而将基站接收的多个时隙干扰信号叠加为零.分析了所提方案在两小区MIMO蜂窝干扰网络中的适用条件、系统和速率和可达自由度,并将该方案与RIA方案和TDMA方案进行对比仿真,结果表明,RIN方案能用更少的时隙数获得更多自由度.
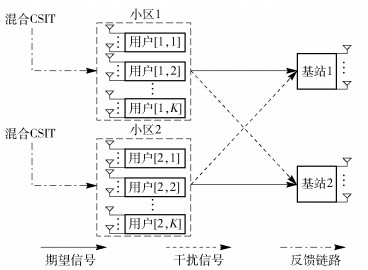
1 蜂窝系统模型两小区MIMO蜂窝干扰网络如图 1所示,记为(M, N, K),图中基站天线数和用户天线数分别为M和N,M≥N且KN>M.每个小区配置1个基站,为K(K≥2)个用户提供服务,用户集记为
|
图 1 混合CSIT反馈的两小区MIMO蜂窝干扰网络 |
| $ {{\mathit{\boldsymbol{y}}}_{l}}\left[ t \right]=\sum\limits_{i=1}^{2}{\sum\limits_{k=1}^{K}{\mathit{\boldsymbol{H}}_{_{l}}^{^{[i, k]}}}}\left[ t \right]{{\mathit{\boldsymbol{x}}}^{[i, k]}}\left[ t \right]+{{\mathit{\boldsymbol{n}}}_{l}}\left[ t \right] $ | (1) |
其中:Hl[i, k][t]为用户[i, k]到基站l的M×N维信道矩阵,假设信道时变,Hl[i, k][t]中的每个元素相互独立,且服从连续分布;x[i, k][t]为用户[i, k]的N×1维发送信号向量;nl[t]~CN(0, σl2IM)为基站l的M×1维复加性高斯白噪声向量.假设接收端(基站)具有完美的接收信道状态信息,用户具有反馈时延为1的混合CSIT,即在时隙t,用户[i, k]获得了前t-1个时隙的信道状态信息{Hl[i, k][t′]}t′=1t-1.同时,在某些时隙t,用户[i, k]还能获得即传的CSIT.事实上,只要反馈时延大于相干时间,即混合CSIT中延时的CSIT是完全过期的,无论反馈时延多大,基于一个时隙反馈时延的RIN方案适用于任意反馈时延情形.
在每个时隙,用户[l, k]上传至基站l的数据可达速率为
| $ {{R}^{[l, k]}}\left( \gamma \right)={{d}^{[l, k]}}\text{lg}\left( \gamma \right)+O(\text{lg}\left( \gamma \right)) $ | (2) |
其中:l∈{1, 2},k∈K,γ为接收信噪比,d[l, k]为用户[l, k]获得的自由度.因此,基站l的可达和速率为
| $ {{R}^{[l]}}\left( \gamma \right)=\sum\limits_{k=1}^{K}{{{R}^{[l, k]}}\left( \gamma \right)} $ | (3) |
上行两小区MIMO蜂窝干扰网络的系统自由度为
| $ D=\sum\limits_{l=1}^{L}{\sum\limits_{k=1}^{K}{{{d}^{[l, k]}}}}=\sum\limits_{l=1}^{2}{\sum\limits_{k=1}^{K}{\underset{\gamma \to \infty }{\mathop{\lim\limits }}\, }}\frac{{{R}^{[l, k]}}\left( \gamma \right)}{\text{lg}\left( \gamma \right)} $ | (4) |
自由度也可以理解为无干扰数据流数.因为噪声不影响自由度,所以在后续讨论中忽略噪声项.
2 RIN方案设计(M, N, K)两小区MIMO蜂窝干扰网络配置任意天线数和小区用户数时,有如下定理.
定理1 具有混合CSIT反馈的上行两小区MIMO蜂窝干扰网络(M, N, K),当N≤M < KN时,其系统自由度为
| $ D=\left\{ \begin{align} &4M/3, \ \ \ N\le M\le KN/2 \\ &M\left( 1+1/\left( 2\varphi +1 \right) \right), \ \ \ KN/2<M<KN \\ \end{align} \right. $ | (5) |
其中φ=「M/(KN-M)⌉为每个用户在边信息提取阶段(步骤1)传输数据流的时隙数.
证明 为了在N≤M < KN范围内的所有配置下获得最优的系统自由度,将其划分为N≤M≤KN/2和KN/2 < M < KN,设计不同的传输方案.首先,考虑范围KN/2 < M < KN,其传输方案如下.
步骤1 边信息提取.该步骤包含2个阶段,每个阶段包含φ个时隙.在第i个阶段(i∈{1, 2}),用户[i, k] (k∈K)在时隙t利用其配置的N根天线发送数据流x[i, k][t]=[x1[i, k], x2[i, k], …, xN[i, k]]T[t],其他用户保持静默. 2个阶段后,基站1和基站2的接收信号中含有期望信号的线性方程为φM个.而在本方案中,步骤2只包含1个时隙,对基站而言,只能提供最多M个线性方程.当KN/2 < M < KN时,能够找到时隙数φ使基站在所有时隙获得的包含期望信号的线性方程数φM+M大于等于未知数KNφ.由于每个基站最多能解码φM+M个数据流,第i个小区的所有用户在φ个时隙内只能传输φM+M个数据流.
在阶段1,小区1中的所有用户在φ个时隙内传输φM+M个数据流和KNφ-φM-M个零元素,小区2的所有用户保持静默.基站l的接收信号为
| $ \begin{array}{c} {\mathit{\boldsymbol{y}}_l}\left[ t \right] = \mathit{\boldsymbol{H}}_{_l}^{^{[1, 1]}}\left[ t \right]{\mathit{\boldsymbol{x}}^{[1, 1]}}\left[ t \right] + \cdots + \mathit{\boldsymbol{H}}_{_l}^{^{[1, K]}}\left[ t \right]{\mathit{\boldsymbol{x}}^{[1, K]}}\left[ t \right] = \\ {\mathit{\boldsymbol{L}}_l}\left[ t \right]({\mathit{\boldsymbol{x}}^{[1, 1]}}, \cdots , {\mathit{\boldsymbol{x}}^{[1, K]}}) \end{array} $ | (6) |
其中t∈T1={1, 2, …, φ}.在阶段1,基站1接收的是期望信号,而基站2接收的是干扰信号,将其保留并在步骤2使用.在阶段1的每个时隙,基站能建立M个线性方程,但有KN个变量.由于KN>M,基站1无法解码所有期望信号.但如果基站1能获取基站2的接收信号L2[t](x[1, 1], …, x[1, K])(t∈T1),那么就有2M个线性方程和KN个变量.当KN/2 < M < KN时,就能解码所有期望信号.因此,关键在于如何将基站2的接收信号L2[t](x[1, 1], …, x[1, K])传递给基站1.
在阶段2,小区2中的所有用户在φ个时隙内传输φM+M个数据流和KNφ-φM-M个零元素,小区1的所有用户静默.基站l的接收信号为
| $ \begin{array}{c} {\mathit{\boldsymbol{y}}_l}\left[ t \right] = \mathit{\boldsymbol{H}}_{_l}^{^{[2, 1]}}\left[ t \right]{\mathit{\boldsymbol{x}}^{[2, 1]}}\left[ t \right] + \cdots + \mathit{\boldsymbol{H}}_{_l}^{^{[2, K]}}\left[ t \right]{\mathit{\boldsymbol{x}}^{[2, K]}}\left[ t \right] = \\ {\mathit{\boldsymbol{L}}_l}\left[ t \right]({\mathit{\boldsymbol{x}}^{[2, 1]}}, \cdots , {\mathit{\boldsymbol{x}}^{[2, K]}}) \end{array} $ | (7) |
其中t∈T2={φ+1, φ+2, …, 2φ}.类似于阶段1的分析,如果基站2能获取基站1的接收信号L1[t](x[2, 1], …, x[2, K]),就能解码所有期望信号.
步骤2 回溯干扰传输.该步骤包括1个时隙.不失一般性,假设2φ+1个时隙具备即时CSIT,令φ=2φ+1.在本传输方案的第2φ+1时隙,用户[1, k]和用户[2, k](k∈K)分别设计预编码矩阵V[1, k][φ]和V[2, k][φ],处理先前时隙已传输过的数据流并发送.每个基站在第2φ+1时隙的接收信号为
| $ \begin{array}{c} {\mathit{\boldsymbol{y}}_l}\left[ {\bar \varphi } \right] = \\ \sum\limits_{k = 1}^K {\mathit{\boldsymbol{H}}_l^{^{[1, k]}}} \left[ {\bar \varphi } \right]{\mathit{\boldsymbol{V}}^{[1, k]}}\left[ {\bar \varphi } \right]\sum\limits_{t = 1}^\varphi {\mathit{\boldsymbol{H}}_2^{^{[1, k]}}} \left[ t \right]{\mathit{\boldsymbol{x}}^{[1, k]}}\left[ t \right] + \\ \sum\limits_{k = 1}^K {\mathit{\boldsymbol{H}}_l^{^{[2, k]}}} \left[ {\bar \varphi } \right]{\mathit{\boldsymbol{V}}^{[2, k]}}\left[ {\bar \varphi } \right]\sum\limits_{t = \varphi + 1}^{2\varphi } {\mathit{\boldsymbol{H}}_1^{^{[2, k]}}} \left[ t \right]{\mathit{\boldsymbol{x}}^{[2, k]}}\left[ t \right] \end{array} $ | (8) |
对用户[i, k](i∈{1, 2}, k∈K)而言,构建N×M维干扰中和矩阵V[i, k][φ]使得基站1和基站2能利用边信息中和,去除第2φ+1时隙接收到的干扰数据流,即
| $ \begin{array}{c} \sum\limits_{k = 1}^K {\mathit{\boldsymbol{H}}_1^{^{[2, k]}}} \left[ {\bar \varphi } \right]{\mathit{\boldsymbol{V}}^{[2, k]}}\left[ {\bar \varphi } \right]\sum\limits_{t = \varphi + 1}^{2\varphi } {\mathit{\boldsymbol{H}}_1^{^{[2, k]}}} \left[ t \right]{\mathit{\boldsymbol{x}}^{[2, k]}}\left[ t \right] + \\ \sum\limits_{t = \varphi + 1}^{2\varphi } {{\mathit{\boldsymbol{L}}_1}\left[ t \right]} ({\mathit{\boldsymbol{x}}^{[2, 1]}}, \cdots , {\mathit{\boldsymbol{x}}^{[2, K]}}) = {\bf{0}} \end{array} $ | (9) |
| $ \begin{array}{c} \sum\limits_{k = 1}^K {\mathit{\boldsymbol{H}}_2^{^{[1, k]}}} \left[ {\bar \varphi } \right]{\mathit{\boldsymbol{V}}^{[1, k]}}\left[ {\bar \varphi } \right]\sum\limits_{t = 1}^\varphi {\mathit{\boldsymbol{H}}_2^{^{[1, k]}}} \left[ t \right]{\mathit{\boldsymbol{x}}^{[1, k]}}\left[ t \right] + \\ \sum\limits_{t = 1}^\varphi {{\mathit{\boldsymbol{L}}_2}\left[ t \right]} ({\mathit{\boldsymbol{x}}^{[1, 1]}}, \cdots , {\mathit{\boldsymbol{x}}^{[1, K]}}) = {\bf{0}} \end{array} $ | (10) |
为了使式(9)和式(10)成立,需满足以下条件:
| $ \mathit{\boldsymbol{H}}_1^{^{[2, k]}}\left[ {\bar \varphi } \right]{\mathit{\boldsymbol{V}}^{[2, k]}}\left[ {\bar \varphi } \right]\mathit{\boldsymbol{H}}_1^{^{[2, k]}}\left[ t \right] + \mathit{\boldsymbol{H}}_1^{^{[2, k]}}\left[ t \right] = {\bf{0}}, t \in {T_2} $ | (11) |
| $ \mathit{\boldsymbol{H}}_2^{^{[1, k]}}\left[ {\bar \varphi } \right]{\mathit{\boldsymbol{V}}^{[1, k]}}\left[ {\bar \varphi } \right]\mathit{\boldsymbol{H}}_2^{^{[1, k]}}\left[ t \right] + \mathit{\boldsymbol{H}}_2^{^{[1, k]}}\left[ t \right] = {\bf{0}}, t \in {T_1} $ | (12) |
由于信道矩阵Hl[i, k][t]为M×N维矩阵,由矩阵的逆矩阵定义可知,Hl[i, k][t]的伪逆Hl[i, k][t]†存在,Hl[i, k][t]†=(Hl[i, k][t]HHl[i, k][t])-1Hl[i, k][t]H.因此,设计V[2, k][φ]=-H1[2, k][φ]†和V[1, k][φ]=-H2[1, k][φ]†,式(9)和式(10)成立,即基站1和基站2能利用边信息消除所有干扰.
下面以基站1为例分析解码过程.基站1在第φ个时隙的接收信号为
| $ \begin{array}{c} \underbrace {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_1}\left[ 1 \right]}\\ {{\mathit{\boldsymbol{y}}_1}\left[ 2 \right]}\\ \vdots \\ {{\mathit{\boldsymbol{y}}_1}\left[ \varphi \right]}\\ {{\mathit{\boldsymbol{y}}_1}\left[ {\bar \varphi } \right] + \sum\limits_{t \in {T_2}} {{\mathit{\boldsymbol{y}}_1}\left[ t \right]} } \end{array}} \right]}_{{{\mathit{\boldsymbol{\bar y}}}_1}} = \\ \underbrace {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}\left[ 1 \right]}&{\bf{0}}&{\bf{0}}&{\bf{0}}\\ {\bf{0}}&{\mathit{\boldsymbol{A}}\left[ 2 \right]}&{\bf{0}}& \vdots \\ \vdots&\vdots&\ddots &{\bf{0}}\\ {\bf{0}}& \cdots &{\bf{0}}&{\mathit{\boldsymbol{A}}\left[ \varphi \right]}\\ {\mathit{\boldsymbol{B}}\left[ 1 \right]}&{\mathit{\boldsymbol{B}}\left[ 1 \right]}& \cdots &{\mathit{\boldsymbol{B}}\left[ \varphi \right]} \end{array}} \right){{\mathit{\boldsymbol{\bar x}}}_1}}_{{{\mathit{\boldsymbol{\bar H}}}_1}} \end{array} $ | (13) |
其中:H2[1, k][t]=H1[1, k][φ]V[1, k][φ]H2[1, k][t],A[t]=[H1[1, 1][t], …, H1[1, K][t]],B[t]=[H2[1, 1][t], …, H2[1, K][t]],x1=[x[1, 1][1]T, …, x[1, K][φ]T]T,k∈K, t∈T1. y1为(φ+1)M×1维接收信号列向量,H1为(φ+1)M×(φ+1)M维等效信道矩阵,x1为(φ+1)M×1维发送信号列向量.信道矩阵的每个元素服从连续分布且相互独立,因此,式(13)中等效信道矩阵H1满秩且秩为(φ+1)M,基站1能解码(φ+1)M个数据流.同理,基站2也能解码(φ+1)M个数据流.由此可知,对于两小区(M, N, K)系统,能在2φ+1个时隙无干扰传输2(φ+1)M个数据流,系统自由度为M×[1+1/(2φ+1)].因为系统自由度随时隙数φ递减,且φ需满足条件φM+M≤KNφ,所以为了最大化系统自由度,时隙数φ取最小值「M/(KN-M)⌉.
对于范围N≤M≤KN/2,选取φ=1,使基站在所有时隙获得的期望信号方程数φM+M大于等于未知数KNφ.利用与范围KN/2 < M < KN相同传输方案和分析可得,系统自由度为4M/3.定理1得证.
3 性能分析以基站1为例计算其可达速率R[1].根据式(13),基站1的接收信号为
| $ {{\mathit{\boldsymbol{\bar y}}}_1} = {{\mathit{\boldsymbol{\bar H}}}_1}{{\mathit{\boldsymbol{\bar x}}}_1} + {{\mathit{\boldsymbol{\bar n}}}_1} $ | (14) |
其中n1=[n1[1], n1[2], …, n1[φ]]T.计算R[1]为
| $ \begin{array}{c} {R^{[1]}} = \\ {\rm{lb}}[{\rm{det}}(\mathit{\boldsymbol{I}} + {{\mathit{\boldsymbol{\bar H}}}_1}E({{\mathit{\boldsymbol{\bar x}}}_1}{({{\mathit{\boldsymbol{\bar x}}}_1})^{\rm{H}}}){({{\mathit{\boldsymbol{\bar H}}}_1})^{\rm{H}}}E{({{\mathit{\boldsymbol{\bar n}}}_1}{({{\mathit{\boldsymbol{\bar n}}}_1})^{\rm{H}}})^{ - 1}})] \end{array} $ | (15) |
系统可达速率为
| $ R = \sum\limits_{l = 1}^2 {{R^{[l]}}} $ | (16) |
首先,通过可达速率仿真对所提RIN方案进行验证;其次,将所提方案所获得的系统自由度与TDMA方案和RIA方案进行分析.仿真分析在平坦瑞利衰落信道环境中进行,信道矩阵元素为独立同分布的高斯变量,且服从CN(0, 1)分布.
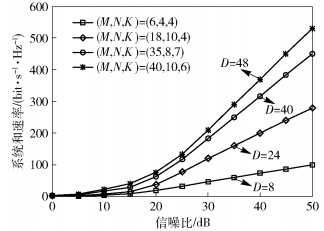
图 2所示为两小区MIMO蜂窝干扰网络不同配置下所提方案的系统和速率与系统自由度.图中任意数值点的值为1万次蒙特卡洛仿真平均值.由香农公式可知,在高信噪比下系统和速率曲线的斜率为D/(10lg2).仿真参数配置参考定理1的约束条件.当N≤M≤KN/2时,选取系统配置为(M, N, K)=(6, 4, 4)和(M, N, K)=(18, 10, 4).当KN/2 < M < KN时,选取系统配置为(M, N, K)=(35, 8, 7)和(M, N, K)=(40, 10, 6).观察图 2可知,当系统配置为(M, N, K)=(6, 4, 4)和(M, N, K)=(18, 10, 4)时,系统自由度分别为8和24且与定理1中4M/3相等.当系统配置为(M, N, K)=(35, 8, 7)和(M, N, K)=(40, 10, 6)时,系统自由度分别为40和48.因为在这2种配置下,传输数据流的时隙数φ=「M/(KN-M)⌉=2,所以可计算出2种系统自由度分别为40和48.仿真结果与定理1的结论一致.
|
图 2 RIN方案的系统和速率与自由度 |
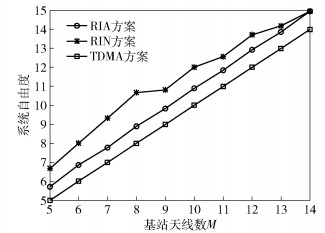
图 3给出了所提RIN方案、RIA方案和TDMA方案的系统可达自由度随基站天线数的变化曲线.仿真参数选择参考定理1的约束条件,用户数K=4,用户天线数N=4,基站天线数M∈[5, 14].由图 3可知,在3种方案的可行性范围内,所提方案获得的系统自由度比RIA方案和TDMA方案高.其主要原因是所提方案能基于混合CSIT更有效地利用基站的信号空间传输更多的无干扰数据流.
|
图 3 3种方案的系统可达自由度比较 |
针对具有反馈时延的上行两小区MIMO蜂窝干扰网络的自由度进行了分析研究,利用所提RIN方案将基站接收的区间干扰叠加为零.分析了所提方案的系统和速率和可达自由度.相比于TDMA方案和RIA方案,所提方案能获得更多的系统自由度.基于笔者的研究和分析,后续可开展基于混合CSIT的上行多小区MIMO蜂窝干扰网络的干扰管理方案设计.
| [1] | Cadambe V R, Jafar S A. Interference alignment and degrees of freedom of the-K user interference channel[J]. IEEE Transactions on Information Theory, 2008, 54(8): 3425–3441. doi: 10.1109/TIT.2008.926344 |
| [2] | Gou Tiangao, Jafar S A, Wang Chengwei. Aligned interference neutralization and the degrees of freedom of the 2×2×2 interference channel[J]. IEEE Transactions on Information Theory, 2012, 58(7): 4381–4395. doi: 10.1109/TIT.2012.2191388 |
| [3] |
谢显中, 王闯, 张森林, 等. 基于干扰对齐的多用户全双工通信中干扰消除方法[J]. 北京邮电大学学报, 2015, 38(6): 87–92.
Xie Xianzhong, Wang Chuang, Zhang Senlin, et al. Interference cancellation based on interference alignment for multiuser full-duplex communications[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(6): 87–92. |
| [4] | Ma Yanjun, Li Jiandong, Chen Rui. On feasibility of interference alignment for L-cell constant cellular interfering networks[J]. IEEE Communications Letters, 2012, 16(5): 714–716. doi: 10.1109/LCOMM.2012.032612.120387 |
| [5] | Shin W, Lee J. Retrospective interference alignment for the two-cell MIMO interfering multiple access channel[J]. IEEE Transactions on Wireless Communications, 2015, 14(7): 3937–3947. doi: 10.1109/TWC.2015.2415474 |
| [6] | Mohanty K, Vaze C S, Varanasi M K. The degrees of freedom region of the MIMO interference channel with hybrid CSIT[J]. IEEE Transactions on Wireless Communications, 2015, 14(4): 1837–1848. doi: 10.1109/TWC.2014.2374169 |


